ММвХТ экзамен. Метод наименьших квадратов

• Название: Метод наименьших квадратов
• Дата: 29.11.2020
• Размер: 1.77 Mb.
• Имя файла: ММвХТ экзамен.docx
• Тип: Документы; #154939
• страница: 3 из 4

17. Меры изменчивости.

В качестве наиболее часто используемых мер изменчивости следует назвать размах, дисперсию, стандартное отклонение.

Размах – это разница между максимальным и минимальным значениями.



Для определения размаха выборку необходимо сначала упорядочить.

Например, в массиве данных {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20} размах будет равен разности между наибольшим и наименьшим значениями, то есть 20 – 8 = 12. но если бы выборка была неупорядочена и имеет большой объем, было бы трудно найти минимальное и максимальное значения.
Дисперсия – это мера разброса данных относительно среднего значения.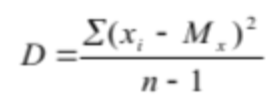



Если вычисление дисперсии производится вручную, то рекомендуется пользоваться специальной таблицей.

Например, необходимо вычислить дисперсию для следующего массива данных {5, 2, 5, 3, 4, 3, 4, 3, 3, 1, 2, 1}.

В соответствии с формулой D = 20 / (12 – 1) = 1,818

Стандартное отклонение представляет собой квадратный корень из дисперсии: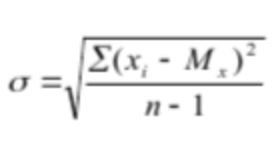



18. Нормальное распределение. Проверка нормальности распределения

Одним из важнейших в математической статистике является понятие нормального распределения. Нормальное распределение (называемое также распределением Гаусса), характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине – часто. Нормальное распределение возникает, когда данная случайная величина представляет собой сумму большого числа независимых случайных величин, каждая из которых играет в образовании всей суммы незначительную роль.

Нормальное распределение имеет колоколообразную форму, значения моды, медианы и среднего арифметического равны между собой. Было установлено, что многие биологические параметры распределены подобным образом (рост, вес и так далее). Впоследствии психологи выяснили, что и большинство психологических свойств (показатели интеллекта, темпераментных особенностей, способностей и другие психические явления) также имеют нормальное распределение. Этот принцип учитывается при стандартизации тестовых методик. При этом, чем больше объем выборки, тем более полученное эмпирическое распределение приближается к нормальному.

Характерное свойство нормального распределения состоит в том, что 68,26 % из всех его наблюдений всегда лежат в диапазоне ± 1 стандартное отклонение от среднего арифметического (какова бы ни была величина стандартного отклонения). 95,44 % - в пределах ± двух стандартных отклонений и 99,72 – в пределах ± трех стандартных отклонений.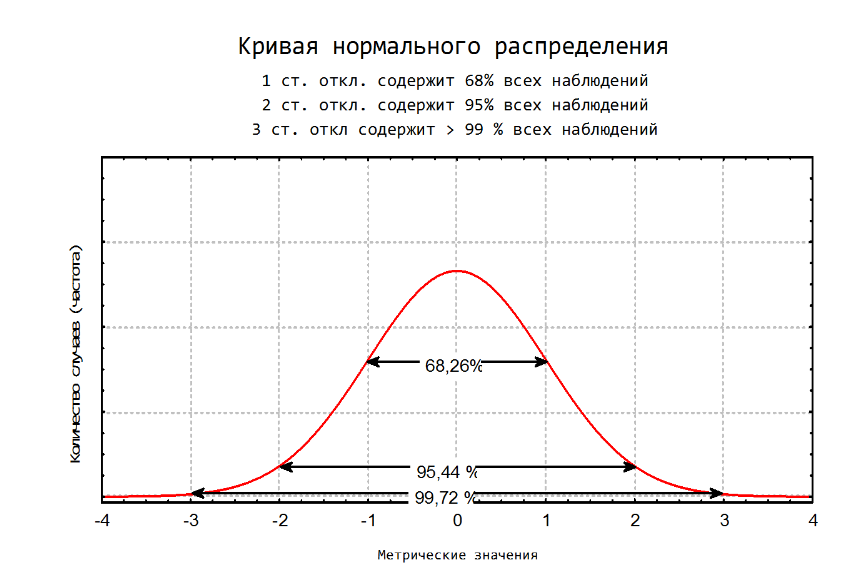



19. Метод корреляций. Коэффициент линейной корреляции

Метод корреляций является методом вторичной статистической обработки. С его помощью выясняется связь или прямая зависимость между двумя рядами экспериментальных данных. Он показывает, каким образом одно явление влияет на другое или связано с ним в своей динамике. Подобного рода зависимости существуют, к примеру, между величинами, находящимися в причинно-следственных связях друг с другом. Если выясняется, что два явления статистически достоверно коррелируют друг с другом и если при этом есть уверенность в том, что одно из них может выступать в качестве причины другого явления, то отсюда определенно следует вывод о наличии между ними причинно-следственной зависимости.

Имеется несколько разновидностей данного метода:

*линейный,

*ранговый,

*парный

*множественный.

Линейный корреляционный анализ позволяет устанавливать прямые связи между переменными величинами по их абсолютным значениям. Эти связи графически выражаются прямой линией, отсюда название «линейный».

Ранговая корреляция определяет зависимость не между абсолютными значениями переменных, а между порядковыми местами, или рангами, занимаемыми ими в упорядоченном по величине ряду.

Парный корреляционный анализ включает изучение корреляционных зависимостей только между парами переменных, а множественный, или многомерный, — между многими переменными одновременно.

Распространенной в прикладной статистике формой многомерного корреляционного анализа является факторный анализ.

На рис. 1 в виде множества точек представлены различные виды зависимостей между двумя переменными X и У (различные поля корреляций между ними).

На фрагменте рис. 1, отмеченном буквой А, точки случайным образом разбросаны по координатной плоскости. Здесь по величине X нельзя делать какие-либо определенные выводы о величине Y. Если в данном случае подсчитать коэффициент корреляции, то он будет равен 0, что свидетельствует о том, что достоверная связь между X и У отсутствует (она может отсутствовать и тогда, когда коэффициент корреляции не равен 0, но близок к нему по величине).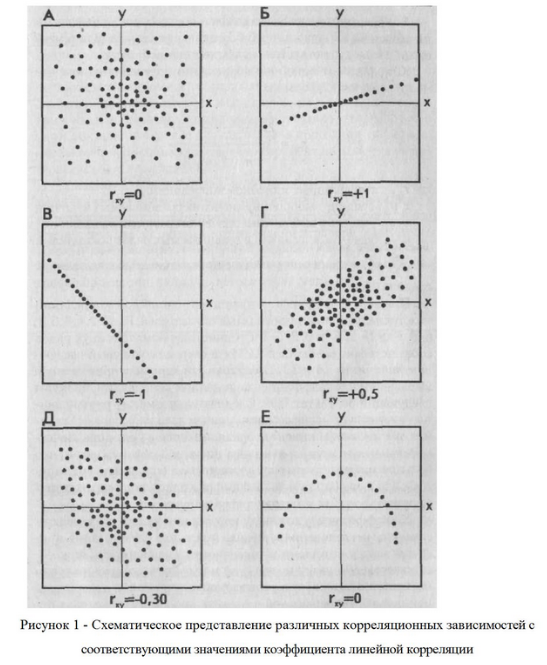



На фрагменте Б рисунка все точки лежат на одной прямой, и каждому отдельному значению переменной X можно поставить в соответствие одно и только одно значение переменной У, причем, чем больше X, тем больше У. Такая связь между переменными X и У называется прямой, и если это прямая, соответствующая уравнению регрессии, то связанный с ней коэффициент корреляции будет равен +1. (Заметим, что в жизни такие случаи практически не встречаются; коэффициент корреляции почти никогда не достигает величины единицы.)

На фрагменте В рисунка коэффициент корреляции также будет равен единице, но с отрицательным знаком: -1. Это означает обратную зависимость между переменными X и У, т.е., чем больше одна из них, тем меньше другая.

На фрагменте Г рисунка точки также разбросаны не случайно, они имеют тенденцию группироваться в определенном направлении. Это направление приближенно может быть представлено уравнением прямой регрессии.

Такая же особенность, но с противоположным знаком, характерна для фрагмента Д. Соответствующие этим двум фрагментам коэффициенты корреляции приблизительно будут равны +0,50 и -0,30. Заметим, что крутизна графика, или линии регрессии, не оказывает влияния на величину коэффициента корреляции.

Наконец, фрагмент Е дает коэффициент корреляции, равный или близкий к 0, так как в данном случае связь между переменными хотя и существует, но не является линейной.

Коэффициент линейной корреляции определяется при помощи следующей формулы:



20. Метод корреляций. Коэффициенту ранговой корреляции

К коэффициенту ранговой корреляции обращаются в том случае, когда признаки, между которыми устанавливается зависимость, являются качественно различными и не могут быть достаточно точно оценены при помощи так называемой интервальной измерительной шкалы.

Интервальной называют такую шкалу, которая позволяет оценивать расстояния между ее значениями и судить о том, какое из них больше и насколько больше другого.

Например, линейка, с помощью которой оцениваются и сравниваются длины объектов, является интервальной шкалой, так как, пользуясь ею, мы можем утверждать, что расстояние между двумя и шестью сантиметрами в два раза больше, чем расстояние между шестью и восемью сантиметрами. Если же, пользуясь некоторым измерительным инструментом, мы можем только утверждать, что одни показатели больше других, но не в состоянии сказать на сколько, то такой измерительный инструмент называется не интервальным, а порядковым.

Некоторые показатели относятся к порядковым, а не к интервальным шкалам (например, оценки типа «да», «нет», «скорее нет, чем да» и другие, которые можно переводить в баллы), поэтому коэффициент линейной корреляции к ним неприменим. В этом случае обращаются к использованию коэффициента ранговой корреляции, формула которого следующая:



Если исходные данные, которые ранжируются, одинаковы, то и их ранги также будут одинаковыми. Они получаются путем суммирования и деления пополам тех рангов, которые соответствуют этим данным.

21.Сравнение дисперсий.

Дисперсия – это мера разброса данных относительно среднего значения.

К параметрическим методам относится и сравнение дисперсий двух выборок по критерию F-Фишера. Иногда этот метод приводит к ценным содержательным выводам, а в случае сравнения средних для независимых выборок сравнение дисперсий является обязательной процедурой.

Метод позволяет проверить гипотезу о том, что дисперсии двух генеральных совокупностей, из которых извлечены сравниваемые выборки, отличаются друг от друга. Проверяемая статистическая гипотеза Н0: При ее отклонении принимается альтернативная гипотеза о том, что одна дисперсия больше другой.

Исходные предположения: две выборки извлекаются случайно из разных генеральных совокупностей с нормальным распределением изучаемого признака.

Структура исходных данных: изучаемый признак измерен у объектов (испытуемых), каждый из которых принадлежит к одной из двух сравниваемых выборок.

Ограничения: распределения признака и в той, и в другой выборке существенно не отличаются от нормального.

Альтернатива методу: критерий Ливена (Levene's Test), применение которого не требует проверки предположения о нормальности (используется в программе SPSS).

Формула для эмпирического значения критерия F-Фишера: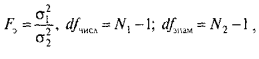



где - большая дисперсия (СКО²), а - меньшая дисперсия (СКО²).

df – число свобод, N– объем выборки.

Так, как заранее не известно какая дисперсия больше, то для определения р-уровня применяется Таблица критических значений для ненаправленных альтернатив. Если Fэ≥Fкр для соответствующего числа степеней свободы, то р≤0,05 и статистическую гипотезу о равенстве дисперсий можно отклонить (для α = 0,05).

Метод может применяться для проверки предположения о равенстве (гомогенности) дисперсий перед проверкой достоверности различия средних по критерию t-Стьюдента для независимых выборок разной численности. Однако содержательная интерпретация статистически достоверного различия дисперсий может иметь и самостоятельную ценность.

22. Критерий t-Стьюдента для одной выборки.

Сравнение двух выборок по признаку, измеренному в метрической шкале, обычно предполагает сравнение средних значений с использованием параметрического критерия t-Стьюдента.

КРИТЕРИЙ t-СТЬЮДЕНТА ДЛЯ ОДНОЙ ВЫБОРКИ

(среднее значение изучаемого признака и постоянного значения)

Метод позволяет проверить гипотезу о том, что среднее значение изучаемого признака Мх отличается от некоторого известного значения А. Проверяемая статистическая гипотеза: Н0: Мх=А. При ее отклонении принимается альтернативная гипотеза о том, что Мх меньше (больше) А.

Исходное предположение: распределение признака в выборке приблизительно соответствует нормальному виду.

Структура исходных данных: значения изучаемого признака определены для каждого члена выборки, которая репрезентативна изучаемой генеральной совокупности.

Альтернатива методу: нет.

Формула для эмпирического значения критерия t-Стьюдента: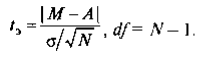

где df – число свобод, N– объем выборки.

ПРИМЕР

Предположим, исследовалось влияние технологического параметра на показатель качества. При использовании выборки были получены следующие результаты: М= 106; σ= 15; N=36. Исследователя интересовало, превышает ли показатель качества нормативный показатель А = 100. Для принятия статистического решения был определен уровень α= 0,05.

Шаг 1. Вычисляем по формуле 11.2 эмпирическое значение критерия и число степеней свободы: tэ= 2,4; df= 35.

Шаг 2. Определяем по таблице критических значений критерия t-Стьюдента (приложение 2) р-уровень значимости. Для df= 35 эмпирическое значение находится между критическими для р = 0,05 и р = 0,01. Следовательно, р <0,05.

Шаг 3. Принимаем статистическое решение и формулируем вывод. Статистическая гипотеза о равенстве среднего значения заданной величине отклоняется. Значение показателя качества (М= 106; σ= 15; N= 36) статистически достоверно превышает нормативный показатель А = 100 (р <0,05).

23. Критерий t-Стьюдента для независимых выборок. (средние значения двух генеральных совокупностей)

Метод позволяет проверить гипотезу о том, что средние значения двух генеральных совокупностей, из которых извлечены сравниваемые независимые выборки, отличаются друг от друга. Допущение независимости предполагает, что представители двух выборок не составляют пары коррелирующих значений признака. Это предположение нарушилось бы, если, например, 1-я выборка состояла из мужей, а 2-я — из их жен, и два ряда значений измеренного признака могли бы коррелировать.

Проверяемая статистическая гипотеза Н0: М1 = М2. При ее отклонении принимается альтернативная гипотеза о том, что М1 больше (меньше) М2.

Исходные предположения для статистической проверки:

* одна выборка извлекается из одной генеральной совокупности, а другая выборка, независимая от первой, извлекается из другой генеральной совокупности;

* распределение изучаемого признака и в той, и в другой выборке приблизительно соответствует нормальному закону;

* дисперсии признака в двух выборках примерно одинаковы (гомогенны).

Структура исходных данных: изучаемый признак измерен у объектов (испытуемых), каждый из которых принадлежит к одной из двух сравниваемых независимых выборок.

Ограничения: распределения признака и в той, и в другой выборке существенно не отличаются от нормального; в случае разной численности сравниваемых выборок их дисперсии статистически достоверно не различаются (проверяется по критерию F-Фишера — при вычислениях «вручную», по критерию Ливена — при вычислениях на компьютере).

Альтернатива методу: непараметрический критерий (U-Манна-Уитни — если распределение признака хотя бы в одной выборке существенно отличается от нормального и (или) дисперсии различаются статистически достоверно.

Формулы для эмпирического значения критерия t-Стьюдента: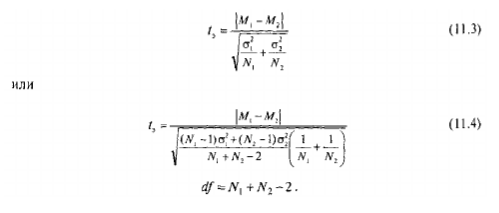

Формула (11.3) применяется для приближенных расчетов, для близких по численности выборок, а формула (11.4) — для точных расчетов, когда выборки заметно различаются по численности.
ПРИМЕР

Предположим, изучалось различие показателя качества для двух видов сырья. Для этого

случайным образом были отобраны 30 значений для первого вида сырья и 28 для второго.

Были получены следующие результаты:



Гипотеза о различии показателя качества проверялась на уровне α= 0,05.

Шаг 1 Вычисляем эмпирическое значение критерия t-Стьюдента по формуле 11.3:

tэ = 2,06 (по формуле 11.4: tэ = 2,17); df= 56

Шаг 2 Определяем по таблице критических значений критерия t-Стьюдента (приложение

2) p-уровень значимости. Для df=56 эмпирическое значение находится между критическими

для р = 0,05 р = 0,01. Следовательно, р < 0,05.

Шаг 3 Принимаем статистическое решение и формулируем вывод. Статистическая

гипотеза о равенстве средних значений отклоняется. Вывод: показатель качества для 2-го

вида сырья статистически достоверно выше, чем у для первого ( р < 0,05).

24. Непараметрические методы сравнения выборок. Критерий серий.

К методам сравнения выборок, в соответствии с принятой классификацией, мы относим способы проверки статистических гипотез о различии выборок по уровню выраженности признака, измеренного в количественной шкале. Непараметрические методы сравнения выборок являются аналогами параметрических методов сравнения средних значений. И почти каждый параметрический метод сравнения средних может быть при необходимости заменен своим непараметрическим аналогом либо сочетанием непараметрических методов.

Непараметрические методы заметно проще в вычислительном отношении, чем их параметрические аналоги. До недавнего прошлого простота вычислений имела существенное значение при обработке данных «вручную». Но, во-первых, данные очень часто включают одинаковые значения, усложняющие расчеты, во-вторых, компьютерная обработка снимает проблему сложности вычислений. Поэтому при выборе между параметрическими и непараметрическими методами следует исходить из свойств самих данных.

Непараметрические аналоги параметрических методов сравнения выборок применяются в случаях, когда не выполняются основные предположения, лежащие в основе параметрических методов сравнения средних значений.

При решении вопроса о выборе параметрического или непараметрического метода сравнения необходимо иметь в виду, что параметрические методы обладают заведомо большей чувствительностью, чем их непараметрические аналоги. Поэтому исходной ситуацией является выбор параметрического метода. И решение о применении непараметрического метода становится оправданным, если не выполняются исходные предположения, лежащие в основе применения параметрического метода.

Условия, когда применение непараметрических методов является оправданным:

* есть основания считать, что распределение значений признака в генеральной совокупности не соответствует нормальному закону;

* есть сомнения в нормальности распределения признака в генеральной совокупности, но выборка слишком мала, чтобы по выборочному распределению судить о распределении в генеральной совокупности;

* не выполняется требование гомогенности дисперсии при сравнении средних значений для независимых выборок.

На практике преимущество непараметрических методов наиболее заметно, когда в данных имеются выбросы (экстремально большие или малые значения).

Если размер выборки очень велик (больше 100), то непараметрические методы сравнения использовать нецелесообразно, даже если не выполняются некоторые исходные предположения применения параметрических методов. С другой стороны, если объемы сравниваемых выборок очень малы (10 и меньше), то результаты применения непараметрических методов можно рассматривать лишь как предварительные.

Структура исходных данных и интерпретация результатов применения для параметрических методов и их непараметрических аналогов являются идентичными.

При сравнении выборок с использованием непараметрических критериев, как и в случае параметрических критериев, обычно проверяются ненаправленные статистические гипотезы. Основная (нулевая) статистическая гипотеза при этом содержит утверждение об идентичности генеральных совокупностей (из которых извлечены выборки) по уровню выраженности изучаемого признака. Соответственно, при ее отклонении допустимо принятие двусторонней альтернативы о конкретном направлении различий в соответствии с выборочными данными. Для принятия статистического решения в таких случаях применяются двусторонние критерии и, соответственно, критические значения для проверки ненаправленных альтернатив.

Перед знакомством с непараметрическими методами сравнения читателю необходимо ознакомиться с порядком и условиями применения их параметрических аналогов.

При выборе того или иного непараметрического метода сравнения выборок можно руководствоваться таблицей классификации методов сравнения (см. рис. 1).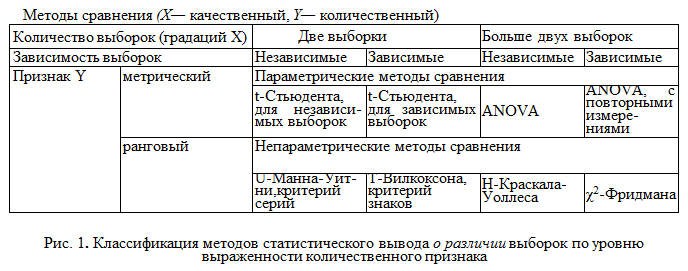



Критерий серий.

Это метод при котором рассчитывается эмпирическое число серий (W), сравнивается с критическим значением числа серий (W_0,025). Если W ≤ W_0,025