Основы теоретической надежности. Методы расчета показателей надежности сжат
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
3. Методы расчета показателей надежности СЖАТ3.1 Статистические оценки показателей надежностиНа основании статистической выборки из 30 значений построить гистограмму частот. Используя критерий Пирсона, убедиться в экспоненциальном законе распределения времени наработки до отказа t. Построить теоретическую функцию плотности распределения a(t). Статистическая выборка для 30 реле времени наработки до отказа представлена в таблице 1. Таблица 1 - Статистическая выборка
Расположим в порядке возрастания значения времени наработки до отказа. После определения интервала Δt, распределим значения выборки в нужный интервал. Результаты сведены в таблицу 2. Таблица 2 – Количество попаданий в интервал
Диапазон значений случайной величины: 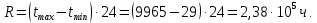 Количество интервалов К: 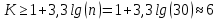 Интервал Δt: 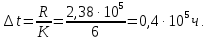 Частоты попадания в i-й интервал: 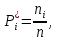 где ni - число попаданий в i-й интервал; n - количество значений в выборке. Статистическую плотность вероятности безотказной работы: 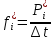 Результаты вычисления приведены в таблице 3. Таблица 3 – Результаты вычисления
На основании данных таблицы 3 построим полигон, гистограмму частот, статистическую функцию распределения Q, рисунки 1, 2 и 3 соответственно. 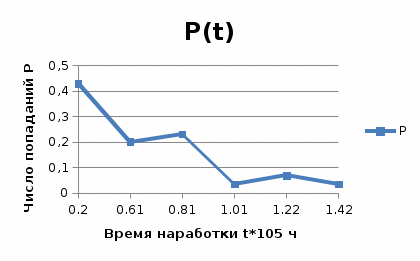 Рисунок 1 – График полигона (частота попаданий в интервал) 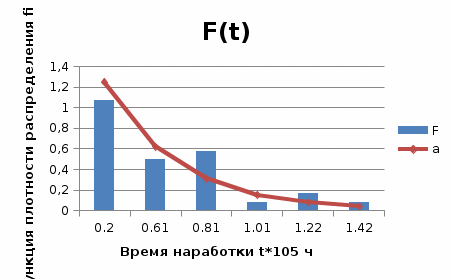 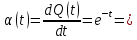 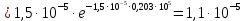 Рисунок 2 – Гистограмма с нанесенной теоретической функцией частоты отказов 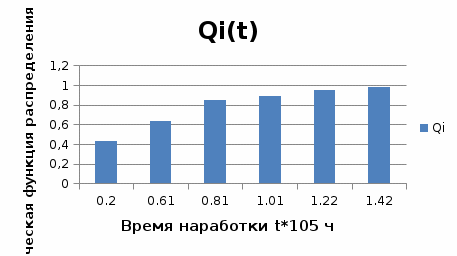 Рисунок 3 – Статистическая функция распределения По виду гистограммы, можно предположить экспоненциальный закон распределения времени наработки t. Примем эту гипотезу и проверим степень ее правдоподобия, используя критерий Пирсона. Для этого построим теоретическую функцию частоты отказов, предполагая экспоненциальный закон распределения для времени наработки: 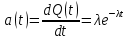 Среднее время наработки до отказа: 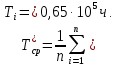 Интенсивность отказов: 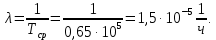 Формула теоретического числа попаданий в i-й интервал: 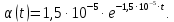 Используя полученное значение интенсивности отказов 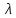 , найдем значения частоты отказов для заданных значений времени наработки , найдем значения частоты отказов для заданных значений времени наработки 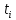 . Эти значения представлены в 7-й строке таблицы 3. Теоретическая кривая функции плотности распределения времени наработки до отказа (частота отказов) представлена на рис. 2. . Эти значения представлены в 7-й строке таблицы 3. Теоретическая кривая функции плотности распределения времени наработки до отказа (частота отказов) представлена на рис. 2. Далее, найдем теоретическое число попаданий в i-й интервал: 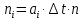 Значения теоретического числа попаданий в i-й интервал ni представлено в 8-й строчке таблицы 2. Мера расхождения между теоретическими числами ni и экспериментальными 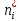 : :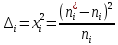 Значения 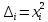 представлены в последней строчке таблицы 3. представлены в последней строчке таблицы 3.Просуммировав значения этого ряда, найдем значение 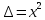 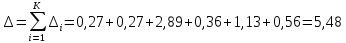 Число степеней свободы Число степеней свободы: 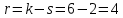 где s – число связей, а k – число интервалов. В таблице 4 представлены значения чисел 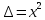 в зависимости от числа степеней свободы r и вероятности . в зависимости от числа степеней свободы r и вероятности .Таблица 4 - значения чисел 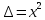 в зависимости от числа степеней свободы r и вероятности . в зависимости от числа степеней свободы r и вероятности .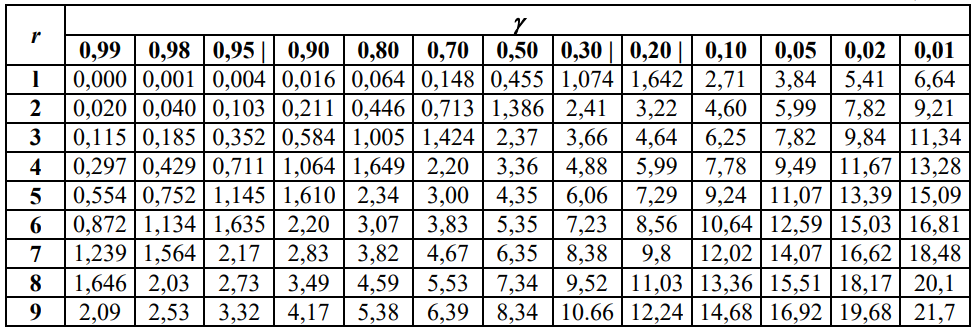 Из таблицы 4 находим значение 0,2. Это значение не превышает порог = 0.3, что свидетельствует о несогласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа. 3.1.2 Статистическая оценка параметров надежности восстанавливаемых устройств На предприятии в момент времени 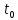 =0 было установлено =0 было установлено 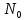 восстанавливаемых устройств. При проверках на промежутках времени восстанавливаемых устройств. При проверках на промежутках времени 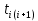 (i = 0, 1, 2) подсчитывалось, сколько устройств отказало на данном промежутке (i = 0, 1, 2) подсчитывалось, сколько устройств отказало на данном промежутке 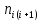 и сколько было восстановлено и сколько было восстановлено 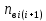 . Найти статистические параметры безотказности и ремонтопригодности на заданном промежутке времени. . Найти статистические параметры безотказности и ремонтопригодности на заданном промежутке времени. Рисунок 4 – Заданный промежуток времени Исходные данные согласно варианту приведены в таблице 5. Таблица 5 - Исходные данные
Заданный промежуток Δ t02=56. За этот промежуток сгорело n02= 168 лампочек, успели восстановить nв02= 140 лампочек. 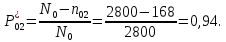 Вероятность отказа: 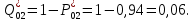 Частоту отказов можно найти по формуле: 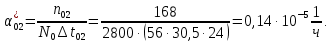 Интенсивность отказов находим по формуле: 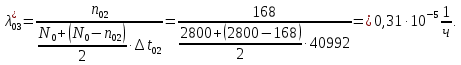 Параметр потока отказов можно оценить по формуле: 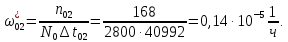 Далее найдем показатели ремонтопригодности. Вероятность восстановления находим по формуле: 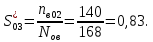 При этом считаем, что число, поставленных на восстановление устройств на начало промежутка N0В, равно числу неисправных устройств на всем рассматриваемом промежутке. Частоту восстановления и интенсивность восстановления найдем по формуле: 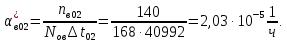 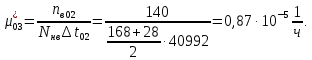 Вывод: Произведя оценку показателей было выяснено, что вероятность безотказной работы лампочек очень высока. Также за определенный промежуток времени было заменено 100% неисправных лампочек, что свидетельствует о максимальной вероятности восстановления. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

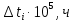
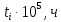
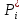
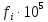 ,1/ч
,1/ч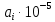 ,1/ч
,1/ч