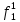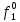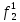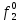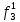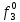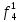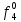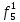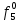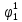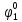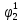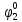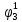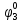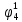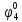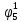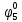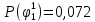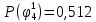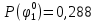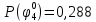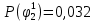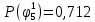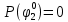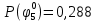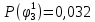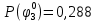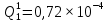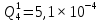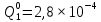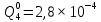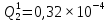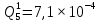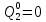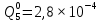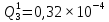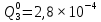Основы теоретической надежности. Методы расчета показателей надежности сжат
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
3.2 Расчет надежности комбинационных схемЛогическая функция в алгебраическом виде: 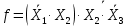 Используя правила синтеза, построим комбинационную схему на двухвходовых логических элементах: 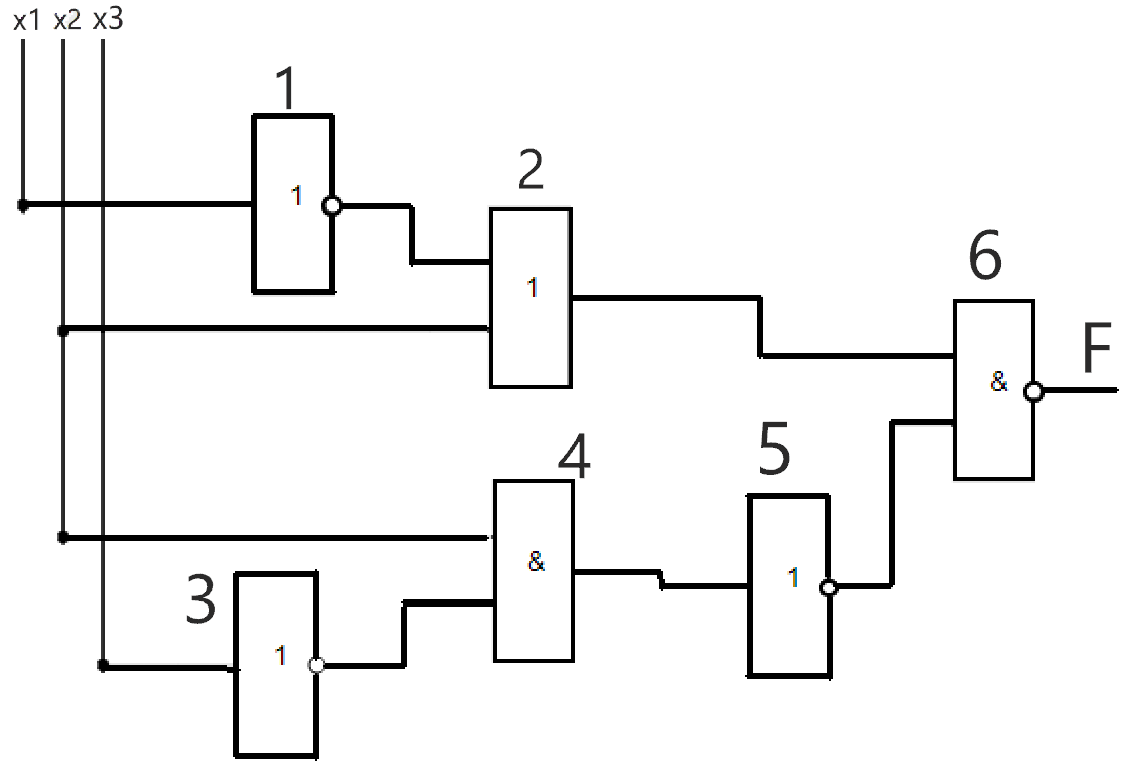 Рис.1. Комбинационная схема на логических элементах Для анализа комбинационной схемы построим таблицу истинности: Таблица 1
Как правило, при расчетах надежности принимается допущение об одиночных константных неисправностях, т.е. считается, что вероятность одновременного проявления двух и более неисправностей настолько мала, что ею можно пренебречь при расчетах. Неисправность логического элемента приводит на выходе элемента к отказам двух видов: Ложному появлению сигнала 1 вместо 0, т.е. на выходе элемента вне зависимости от состояния входа всегда присутствует логическая «1»; Ложному появлению сигнала 0 вместо 1, т.е. на выходе элемента вне зависимости от состояния входа всегда присутствует логический «0». Функцией ошибки 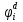 называется функция, принимающая значение «1» на тех и только тех входных наборах, на которых функция, реализуемая исправной схемой – f, и функция, реализуемая неисправной схемой – fi, принимают различные значения. называется функция, принимающая значение «1» на тех и только тех входных наборах, на которых функция, реализуемая исправной схемой – f, и функция, реализуемая неисправной схемой – fi, принимают различные значения.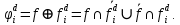 Функции, реализуемые неисправной схемой 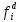 и функцией ошибки и функцией ошибки 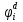 сведены в Таблицу 6. сведены в Таблицу 6.Таблица 2
Произведя подобные вычисления для сбоев типа 0 1 и 1 0 всех шести элементов схемы, получим: Функции ошибки в десятичном виде: 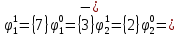 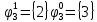 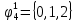 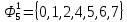 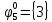 Вероятности появления входных переменных 𝑝1= 0,2; 𝑝2= 0,4; 𝑝3= 0,9. Определим вероятности Rk появления входных наборов и составим таблицу, отражающую полную группу событий на входе схемы: Таблица 3
Вероятность истинности функции f: 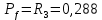 Вероятности истинности функции ошибки:
Вероятность появления неисправности в момент времени t для каждого элемента:
Вероятность ошибки на выходе схемы в момент времени t: 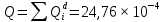 Вероятность исправной работы схемы: 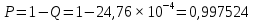 |