Основы теоретической надежности. Методы расчета показателей надежности сжат

• Название: Методы расчета показателей надежности сжат
• Анкор: Основы теоретической надежности
• Дата: 21.12.2022
• Размер: 0.91 Mb.
• Имя файла: OTN_polnostyu_gotovy_Chirkov_28_variant (3).docx
• Тип: Курсовая; #857127
• страница: 2 из 8

Оглавление

1. Особенности надежности и безопасности СЖАТ 8

2. Показатели надежности для невосстанавливаемых и восстанавливаемых систем 11

3. Методы расчета показателей надежности СЖАТ 18

3.1 Статистические оценки показателей надежности 18

3.2 Расчет надежности комбинационных схем 25

3.3 Расчет показателей надёжности восстанавливаемых систем методом Марковских процессов 28

3.4 Структурный метод расчета надежности 38

3.5 Топологический метод расчета надежности резервированных систем 41

3.6 Расчет эксплуатационной надежности СЖАТ 45

Заключение 52

Список литературы 55

1. Особенности надежности и безопасности СЖАТ

Надежность систем железнодорожной автоматики и телемеханики (СЖАТ) – это свойство устройств СЖАТ обеспечивать во времени бесперебойное и безопасное движение поездов в заданных режимах, условиях применения, технического обслуживания, хранения и транспортировки.

Классификация возможных состояний объекта ЖАТ (Рис. 1.1) определяется соответствием или несоответствием объекта требованиям нормативно-технической и конструкторской документации: в исправном состоянии объект полностью соответствует этим требованиям, в неисправном – не соответствует хотя бы одному из них.

В работоспособном состоянии значения всех параметров объекта, характеризующих его способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской документации. В неработоспособном состоянии хотя бы один такой параметр не удовлетворяет требованиям нормативно-технической и (или) конструкторской документации. Предельным называют состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна – например, вследствие износа.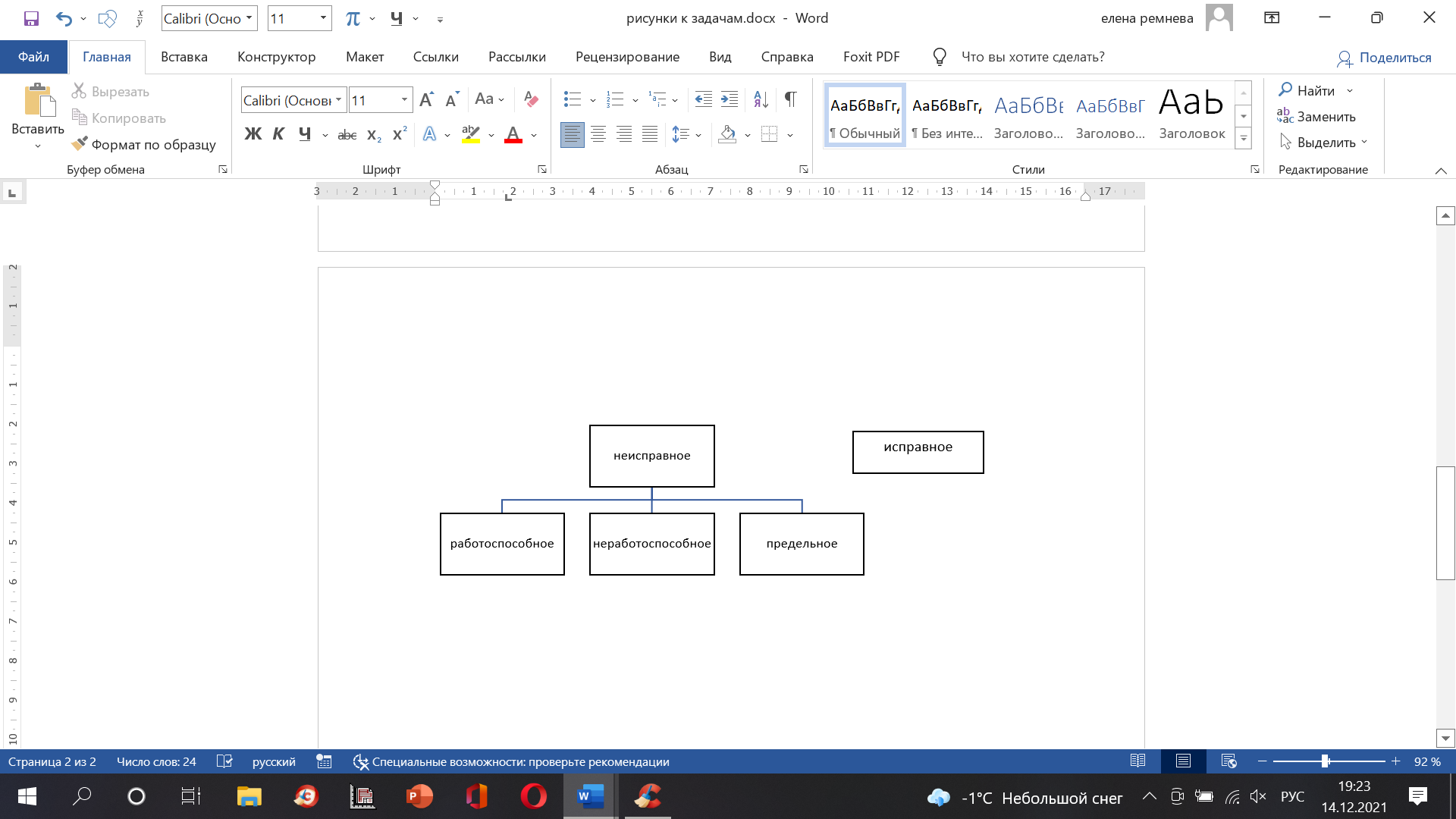



Рис. 1.1 - Состояния, в которых может находиться объект ЖАТ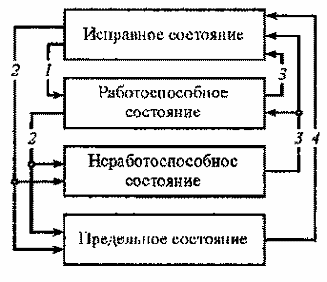





1 – повреждение

2 – отказ

3 – ремонт

4 – капитальный ремонт


Рис. 1.2. - Схема связей между состояниями объекта

Надежность СЖАТ как сложное свойство объединяет понятия:

1) безопасность – свойство объекта непрерывно сохранять исправное, работоспособное или защитное состояние (Рис. 1.3) в течение некоторого времени

2) безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени

3) долговечность – свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта

4) ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений и поддержанию, и восстановлению работоспособного состояния в результате проведения технического обслуживания и ремонтов

5) сохраняемость – свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в процессе хранения и после него и/или в процессе транспортирования.


1 – повреждение

2 – защитный отказ

3 – ремонт

4 – капитальный ремонт

5 – опасный отказ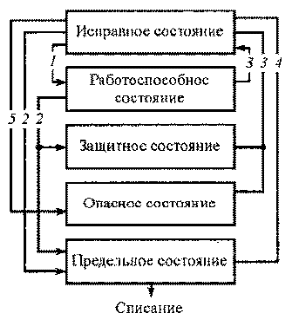


Рис. 1.3. - Схема связей между состояниями СЖАТ

2. Показатели надежности для невосстанавливаемых и восстанавливаемых систем

Показатель надежности – это количественная характеристика одного или нескольких свойств, составляющих надежность объекта.

Показатель надежности количественно характеризует, в какой степени объекту присущи определенные свойства надежности. В зависимости от того, сколько свойств надежности характеризуют показатели, различают единичные и комплексные показатели надежности: единичные характеризуют одно из свойств, комплексные - не менее двух. При определении надежности объектов используют две формы представления показателей - вероятностную и статистическую. Вероятностная форма удобна для аналитических расчетов, статистическая - при проведении экспериментальных исследований и испытаний объектов на надежность.

Показателями надежности невосстанавливаемых объектов являются:

• 
  вероятность безотказной работы P(t);
  
• 
  вероятность отказа Q(t);
  
• 
  частота отказов f(t);
  
• 
  интенсивность отказов X(t);
  
• 
  средняя наработка до отказа Т_о (наработка до отказа).
  

Вероятность безотказной работы – вероятность того, что в пределах заданной наработки отказ объекта не возникнет. Под наработкой понимается продолжительность или объем работы объекта. Статистическая оценка вероятности безотказной работы может быть получена в результате испытаний на надежность: в интервале времени (или наработки) от t₁ до t₂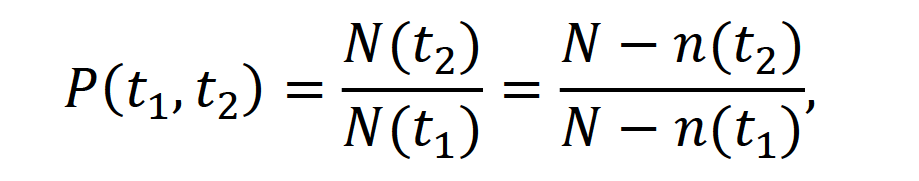



где N(t₁), N(t₂) - число работоспособных объектов, соответственно на начало и конец интервала времени, n(t₁), n(t₂) - число отказавших объектов, соответственно на начало и конец интервала времени.

Вероятность отказа Q(t) - вероятность того, что в пределах заданной наработки объект откажет хотя бы один раз.

С 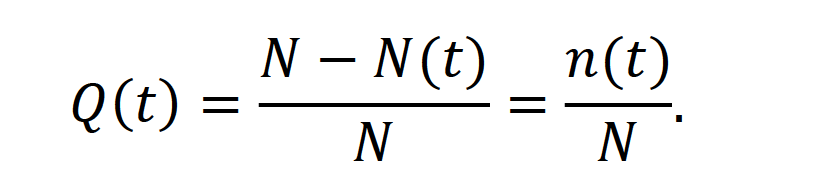татистическая оценка вероятности отказа за время или наработку

Работоспособное и неработоспособное состояния - противоположные несовместные состояния, образующие полную группу возможных состояний объекта, поэтому в любой момент времени или при любой наработке P(t) + Q(t) = 1.

Для описания мгновенных значений показателей надежности применяется дифференциальная функция - частота отказов или плотность распределения наработки до отказа: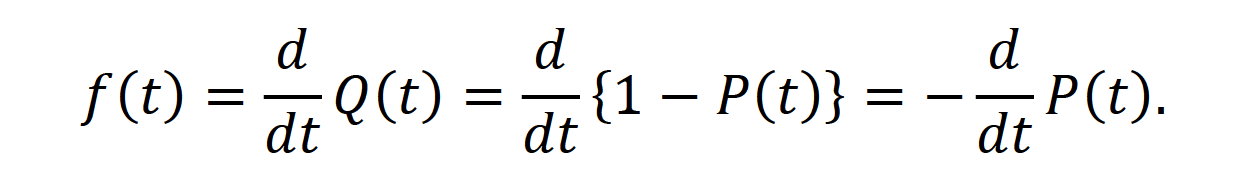



Статистическая оценка частоты отказов f(t) определяется отношением числа отказавших объектов в единицу времени к числу поставленных на испытание объектов при условии, что отказавшие объекты не заменяются новыми:



где n(Δt) - число отказов объектов за рассматриваемый промежуток времени Δt; N - число объектов, поставленных на испытание.

Важнейшей характеристикой безотказности невосстанавливаемых объектов является интенсивность отказов λ(t).

Интенсивность отказов – условная плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента времени отказ не возник.

Аналитически интенсивность отказов определяется как отношение ч 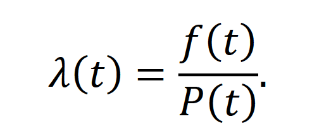астоты отказов к вероятности безотказной работы:

С 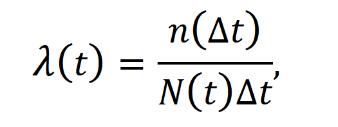татистическая оценка интенсивности отказов:

где Δ(t) = [N(t₁) + N(t₂)]/2 - среднее число работоспособных объектов в интервале времени Δt.

Опыт исследования технических систем показывает, что интенсив­ность отказов λ(t) в течение времени изменяется так, как показано на Рис. 2.1.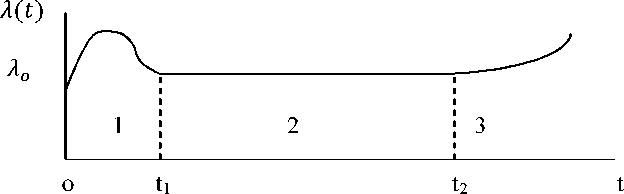



Рис. 2.1
График функции λ(t) условно можно разделить на три участка - период приработки, нормальной работы и деградации. На первом участке интенсивность отказов сначала растет, а затем уменьшается с течением времени. На этом участке выявляются скрытые дефекты производства и монтажа систем. Участок носит название участка приработки. Второй участок считается периодом нормальной эксплуатации. Он характеризуется относительно постоянным значением интенсивности отказов. Здесь проявляются главным образом внезапные отказы, прежде всего из-за случайных изменений нагрузки, неблагоприятных условий эксплуатации. На третьем участке проявляется усиление старения, износа элементов. Вследствие этого интенсивность отказов начинает возрастать. При достижении времени t₂ объект, как правило, должен сниматься с эксплуатации.

Наработка до отказа - наработка объекта от начала эксплуатации до возникновения первого отказа. Аналитически наработка до отказа определяется как: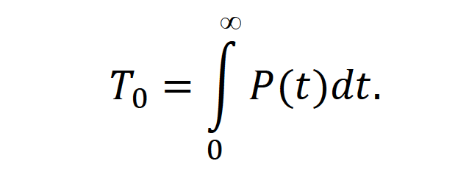




С 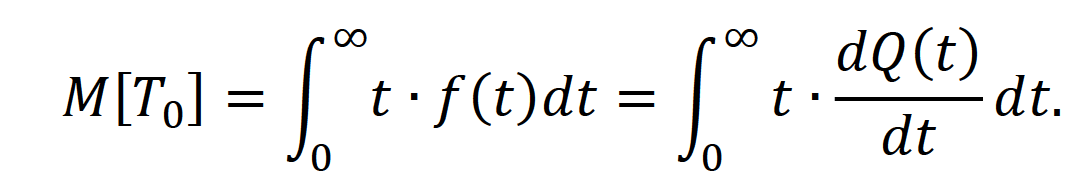редняя наработка до отказа - математическое ожидание наработки объекта до отказа:

Статистическая оценка средней наработки до отказа: где N- число объектов, поставленных на испытание, t_pi- время работы /-го объекта до первого отказа.



Н 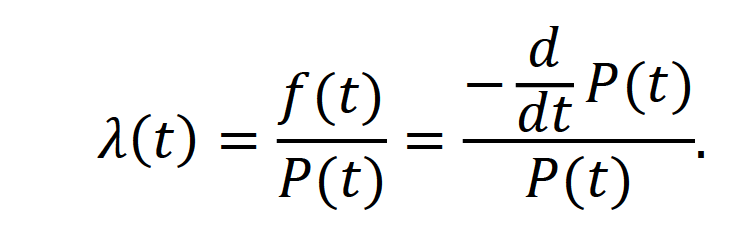а основе определения интенсивности отказов имеет место равенство:

П 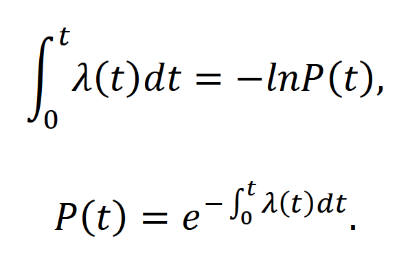осле интегрирования этого выражения получим:

Последнее уравнение - одно из основных в теории надежности. Из него следует, что вероятность безотказной работы представляет собой экспоненциальную монотонно убывающую функцию, которая в интервале времени или наработки от t= 0 до t= х> изменяется от 1 до 0. Соответственно, вероятность отказа меняется в том же интервале от 0 до 1. Такой закон получил название экспоненциального закона надежности.

Для восстанавливаемых объектов характерно чередование работоспособного состояния и восстановления работоспособности после отказа (Рис. 2.2). Таким образом, процесс эксплуатации объекта можно представить как последовательное чередование случайных событий интервалов времени работоспособного t_pi и неработоспособного состояний t_Вi.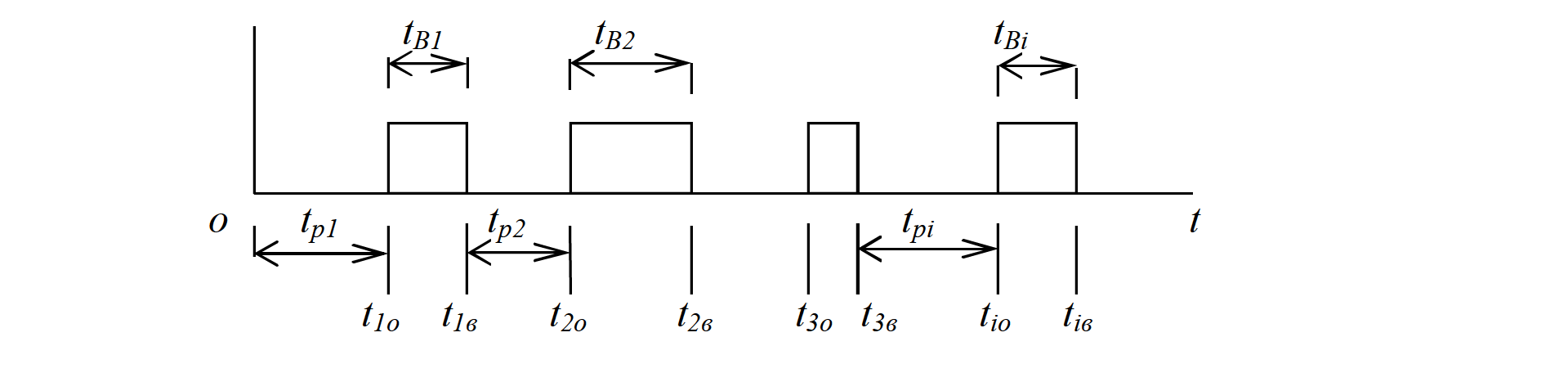


Рис. 2.2

Моменты отказов t_lo, t_2o, …, t_io образуют поток событий отказов, а моменты окончания восстановления t_1в, t_2в, …, t_iв образуют поток событий восстановлений. Указанные потоки представляют собой случайные процессы.

Случайный поток событий, функция распределения которого подчиняется экспоненциальному закону 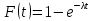, называется потоком Пуассона. В данном случае λ (среднее число событий в единицу времени) называется интенсивностью случайного потока.

Д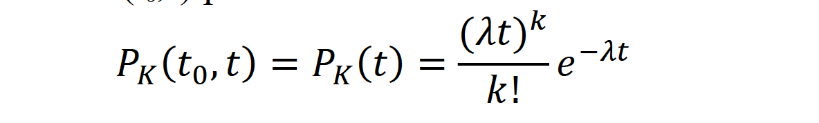
ля пуассоновского потока вероятность наступления ровно k событий в промежутке времени (t₀,t) равна:

и не зависит от времени t₀, то есть в пуассоновском потоке время ожидания нового события не зависит от времени, прошедшего после последнего со­бытия. Для пуассоновского потока математическое ожидание с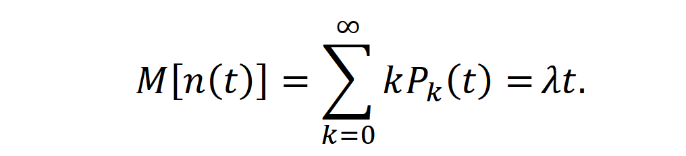
лучайного числа отказов n(t) событий за время t равно:

Пуассоновский поток обладает следующими свойствами:

1. 
   Стационарностью - вероятностные характеристики потока для любого интервала времени зависят только от длительности этого интервала и не зависят от момента его начала.
   
2. 
   Ординарностью - в бесконечно малом интервале времени вероятность появления двух и более событий бесконечно мала. То есть, в один и тот же момент времени появление более одного отказа невозможно.
   
3. 
   Отсутствием последействия - начиная с некоторого момента времени вероятность появления отказа в рассматриваемом интервале времени не зависит от того, сколько было отказов до момента начала рассматриваемого промежутка времени. Отсутствие последействия выражает взаимную независимость отказов.
   

Для анализа надежности восстанавливаемых объектов используются следующие показатели:

• 
  ω(t) - параметр потока отказов;
  
• 
  Т - среднее время работы между отказами (средняя наработка на отказ);
  
• 
  P(t) - вероятность безотказной работы;
  
• 
  Q(t) - вероятность отказа.
  

Параметр потока отказов ω(t) – это отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки.


где n(t) - число отказов объекта за наработку t.

С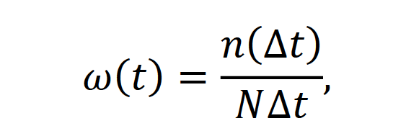
татистическая оценка параметра потока отказов:

где n(Δt) - число отказов в рассматриваемом промежутке времени Δt; N- число объектов, поставленных на испытания, при условии, что отказавшие объекты восстанавливаются или заменяются аналогичными, но новыми. Размерность параметра потока отказов – [1/ч].

Если поток отказов стационарен, то ω(t) = ω = λ. То есть в системах железнодорожной автоматики и телемеханики понятия «интенсивность отказов» и «параметр потока отказов» можно считать идентичными.

Для ординарных потоков при известном параметре потока отказов можно

определить математическое ожидание числа отказов n(t) за время t.


Для стационарного потока отказов ω = const, тогда n(t) = ωt.

Время работы между отказами - наработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа.

С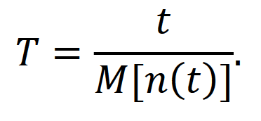
редняя наработка на отказ Т (наработка на отказ) – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки:

Статистическая оценка времени наработки на отказ:

П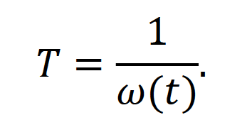
ри известном параметре потока отказов наработка на отказ равна:

С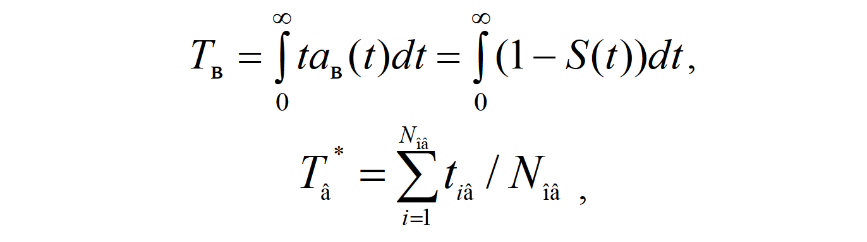
реднее время восстановления T - математическое ожидание времени восстановления работоспособного состояния объекта:

Пусть интенсивность восстановления не зависит от времени A(t) = A= const . Практически это означает, что производительность труда ремонтных бригад сохраняется постоянной. Коэффициент готовности K_г - вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени: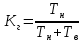



Коэффициент готовности - комплексный показатель надежности, который учитывает и безотказность и ремонтопригодность.

В
ероятность безотказной работы восстанавливаемого объекта в рассматриваемом интервале наработки:

В
ероятность отказов: