Методическая разработка по выполнению контрольной работы для студентов факультета второго высшего и дополнительного образования
 Скачать 1.29 Mb.
|
|
Федеральное агентство по образованию САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра статистики СТАТИСТИКА МЕТОДИЧЕСКАЯ РАЗРАБОТКА по выполнению контрольной работы для студентов факультета второго высшего и дополнительного образования Самара Издательство Самарского государственного экономического университета 2010 Статистика [Текст]: метод. разработка по выполнению контрольной работы для студентов факультета второго высшего и дополнительного образования / сост.: Т.И. Леонтьева, О.В. Баканач, Н.В. Проскурина. - Самара: Изд-во Самар. гос. экон. ун-та, 2010. - 64 с. Методическая разработка содержит краткий обзор основных понятий и примеры решения типовых задач по каждой теме курса статистики. Окажет помощь при написании, оформлении и защите контрольной работы по данной дисциплине. Приведены также варианты контрольной работы и примерные тесты к экзамену (зачету). Предназначена для студентов факультета второго высшего и дополнительного образования, изучающих дисциплину "Статистика ". Печатается по решению редакционно-издательского совета университета Составители: канд. экон. наук, доц. Т.И. Леонтьева канд. экон. наук, доц. О.В. Баканач канд. экон. наук, доц. Н.В. Проскурина © Самарский государственный э  кономический университет, 2010СОДЕРЖАНИЕ Введение 4 Рекомендации по оформлению контрольной работы 4 Методические указания по выполнению задач 5 Варианты контрольной работы 24 Примерные тесты к экзамену (зачету) 44 Контрольные вопросы по курсу 61 Библиографический список 62 ВВЕДЕНИЕ Целью изучения студентами курса "Статистика " является приобретение навыков в области методологии статистического анализа экономической информации. Статистика служит инструментом в работе экономистов высшей квалификации: менеджеров, бухгалтеров, аудиторов, финансистов и др. В результате изучения дисциплины студенты должны: знать принципы и методы сбора статистической информации; владеть методикой ее обобщения; выполнять статистический анализ данных; уметь интерпретировать полученные результаты и обоснованно формулировать выводы. РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ Контрольная работа выполняется с целью закрепления и проверки знаний, полученных студентами в процессе самостоятельного изучения учебного материала, а также для выявления их умения применять на практике методы статистики. Приступая к осуществлению работы, необходимо ознакомиться с соответствующими разделами курса, изучить рекомендованную литературу, уделить особое внимание методике построения и технике расчета и анализа статистических показателей. К выполнению контрольной работы предъявляются следующие требования: 1) работа выполняется в рукописном или печатном вариантах, обязательно приводится номер задания, текст условия задач; 2) решение следует начинать с теоретического обоснования и приведения необходимых формул; 3) расчеты должны быть развернутыми, содержать пояснения; 4) если возможны несколько методов расчета того или иного показателя, следует применять наиболее простой из них, указав при этом и другие способы решения; 5) проверка правильности выполнения расчетов должна осуществляться на основе взаимосвязи показателей с учетом их экономического содержания; 6) все записи следует делать разборчиво, используя лишь общепринятые сокращения слов; 7) расчет относительных величин следует производить с точностью до 0,001 (до 0,1%); 8) при необходимости решения задач оформляются с использованием статистических таблиц и графиков, которые следует строить в соответствии с правилами, принятыми в статистике; 9) по результатам расчетов должны быть сделаны краткие выводы; 10) страницы работы должны быть пронумерованы; для замечаний рецензента оставляются поля. После рецензирования необходимые исправления выполняются в конце работы после рецензии; 11) в заключении работы необходимо привести список использованной литературы, поставить свою подпись и указать дату выполнения. Вариант заданий выбирается в соответствии с начальной буквой фамилии студента:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАЧ Задача 1 предполагает освоение студентами важнейшего статистического метода изучения взаимосвязей общественных явлений - аналитических группировок. На основе аналитической группировки определяют наличие и направление связи между изучаемыми признаками. Группировка строится по факторному признаку, оказывающему влияние на связанные с ним результативные признаки. Число выделяемых групп определяется в соответствии с условием конкретной задачи. При группировке с равными интервалами величина интервала определяется по формуле  где  - соответственно, наибольшее и наименьшее значения группировочного признака в совокупности;к - число выделяемых групп. Например, по данным задачи 1 (вариант 1), величина интервала составит:  Каждая из выделенных групп характеризуется показателями, соответствующими условиям задач. Результаты группировки оформляются в виде статистической таблицы. Например, макет групповой таблицы задачи 1 (вариант 1) будет иметь следующий вид: Группировка предприятий отрасли по среднегодовой стоимости основных фондов и объему продукции
По результатам группировки необходимо сделать вывод о том, как с изменением факторного признака по выделенным группам изменяются значения результативного признака. Выполнение задачи 2 позволит студентам овладеть методикой расчета относительных величин плана, реализации плана, динамики, структуры, сравнения, интенсивности, координации. Задачи 3-4 предполагают вычисление количественных характеристик статистических рядов распределения: средних величин, показателей вариации и показателей структурных различий. При расчете средней величины в интервальном ряду распределения необходимо определить середину каждого интервала как среднюю арифметическую простую из его границ. Величина открытых интервалов (где указана только одна, нижняя или верхняя, граница) условно принимается равной величине соседнего закрытого интервала. Далее расчет осуществляется по формуле средней арифметической взвешенной 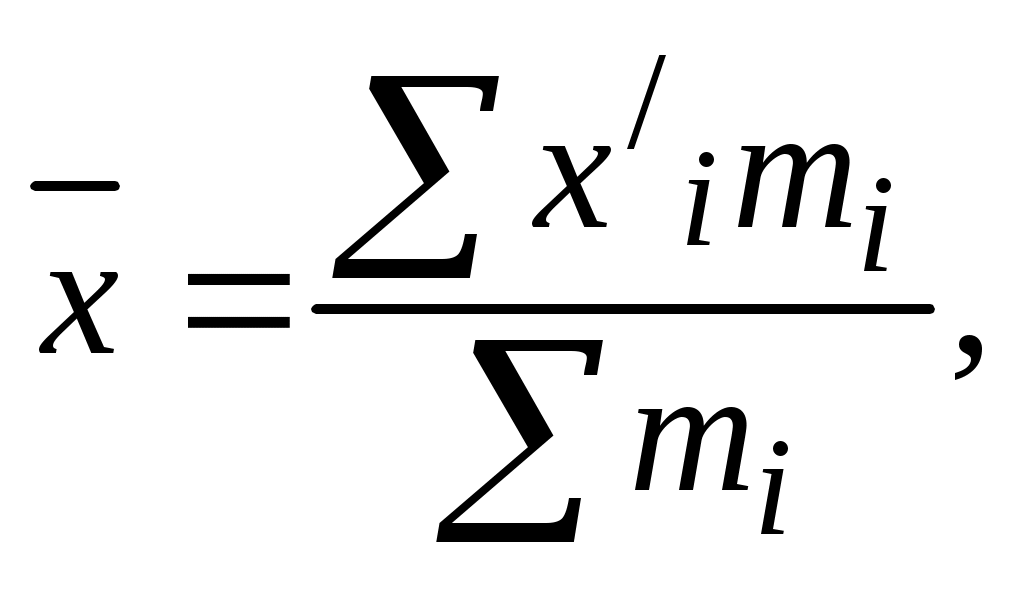 где  - середины интервалов;т - число повторений значений признака. Следует иметь в виду, что в качестве веса отдельных вариантов могут быть использованы не только абсолютные значения частот, но и относительные - частости (доли, проценты к итогу). Колеблемость признака в совокупности характеризуют показатели вариации: среднее линейное отклонение определяется как средняя из абсолютных значений отклонений отдельных вариантов от их средней величины:  среднее квадратическое отклонение рассчитывается как корень квадратный из дисперсии. Дисперсия представляет собой среднюю из квадратов отклонений отдельных вариантов от их средней величины: 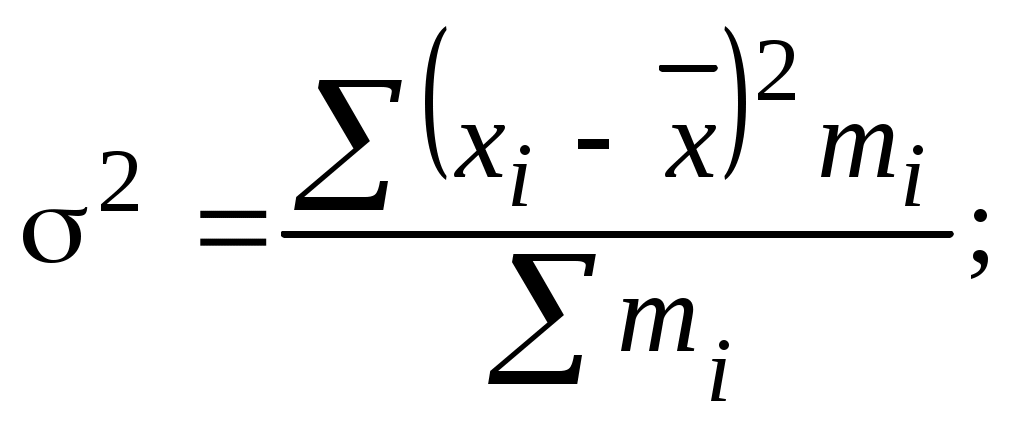 коэффициент вариации определяется по формуле  Модой в статистике называют значение признака, которое наиболее часто встречается в изучаемой совокупности. Для интервального ряда распределения значение моды определяется приближенно по формуле  где х0 - нижняя граница модального интервала, т.е. интервала, которому соответствует наибольшая частота (частость); i- величина модального интервала; m2 - частота или частость модального интервала (наибольшая в ряду распределения); m1 - частота или частость модального интервала, предшествующая модальному; m3 - частота или частость интервала, следующего за модальным. Медиана - значение признака, расположенное в середине ранжированного ряда распределения. Половина единиц совокупности имеет значение признака больше медианы, другая половина - меньше. Для интервального ряда распределения значение медианы рассчитывается по формуле  где х0 - нижняя граница медианного интервала (медианный - первый интервал, накопленная частота которого превысила половину общей суммы частот); i- величина медианного интервала;  - сумма всех частот ряда; - сумма частот, накопленных до медианного интервала;m- частота медианного интервала. Аналогично медиане определяются децили - структурные средние, отделяющие в совокупности десятые части. Дециль первого порядка отделяет 10% единиц с наименьшими значениями признака, дециль девятого порядка - соответственно, 10% единиц с наибольшими значениями: 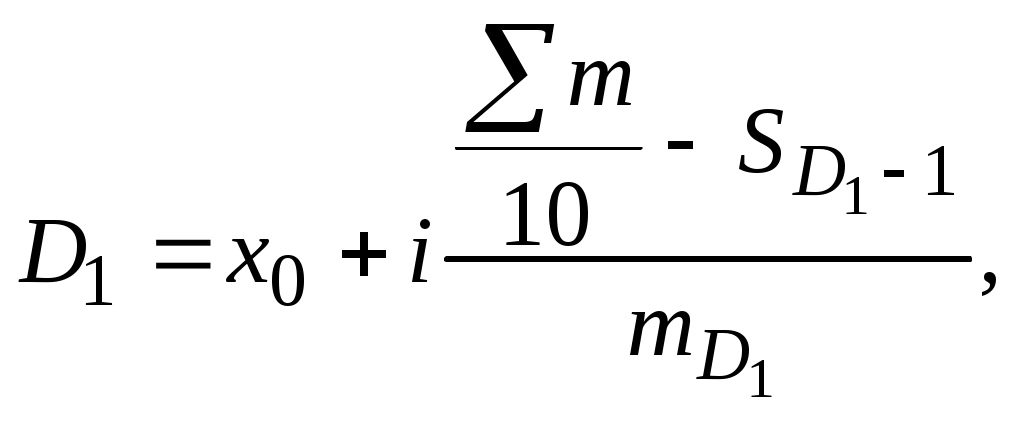 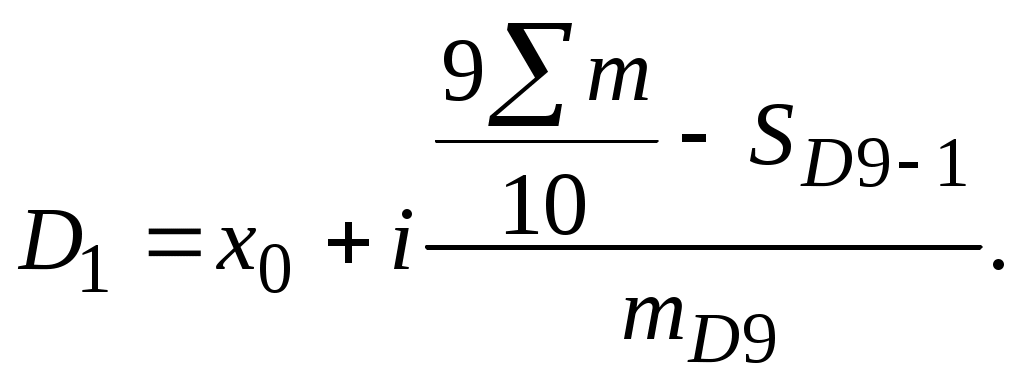 Децильный коэффициент дифференциации рассчитывается отношением децили девятого порядка к децили первого порядка. Пример решения задачи 3 По данным выборочного обследования получено следующее распределение работников организации по размеру заработной платы:
Определите: 1) среднюю заработную плату; 2) коэффициент вариации; 3) моду и медиану. Решение 1. Условие задания представлено интервальным вариационным рядом с равными интервалами. Поэтому для вычисления показателей сначала следует определить величину осредняемого признака (х) как середину каждого интервала и получить дискретный ряд распределения.
Далее производим расчет по средней арифметической взвешенной: 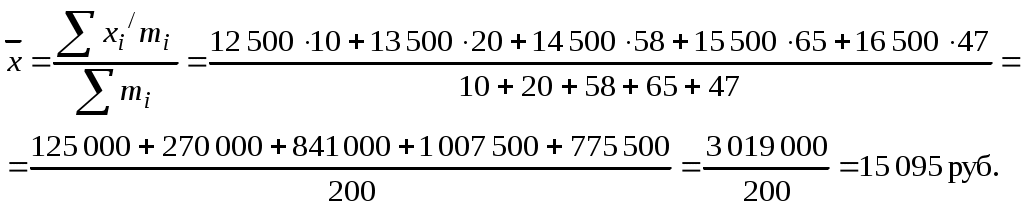 2.Коэффициент вариации характеризует меру колеблемости отдельных вариантов признака (х) вокруг средней величины. Он представляет собой процентное соотношение среднего квадратического отклонения (σ) и средней арифметической  , т.е. Для расчета среднего квадратического отклонения предварительно вычислим дисперсию (σ2)по формуле 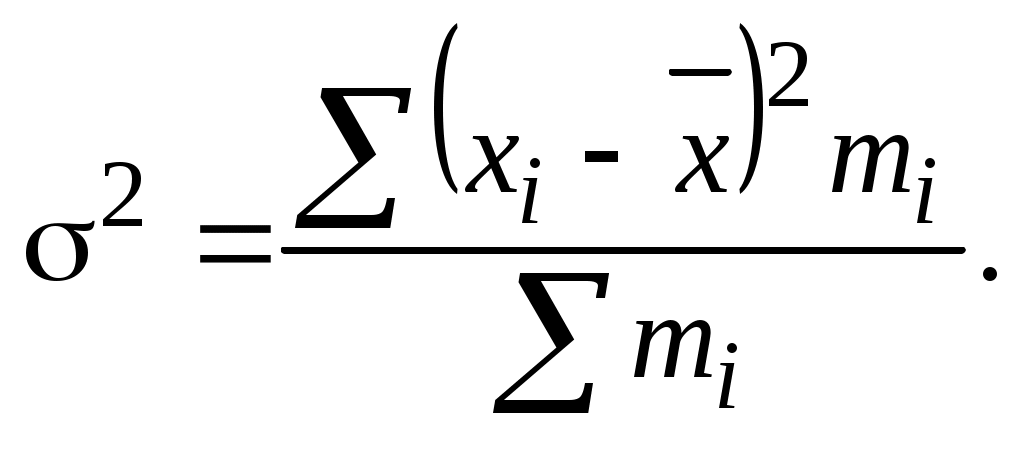 Расчет можно выполнить с помощью вспомогательной таблицы:
 Среднее квадратическое отклонение - это корень квадратный из дисперсии: σ = ±√ σ2 = ±  ±1100,443 руб.Коэффициент вариации составит:  Если значение коэффициента вариации не превышает 33,3%, то совокупность считается однородной, а средняя величина может быть признана типичной для данного распределения. В нашем примере средняя величина типична. 3. Мода (доминанта) - это наиболее часто встречающееся значение признака x; в интервальном ряду модальным будет тот интервал, который имеет наибольшую частоту (частость). В данном задании наибольшую частоту (65) имеет интервал 15 000 - 16 000 руб., следовательно, мода и будет находиться в этом интервале.  руб.Следовательно, наибольшее число работников имели заработную плату в размере 15 280 руб. Медиана - значение признака у той единицы ранжированного ряда, которая находится в его середине. Сначала определим порядковый номер этой единицы. Для этого добавим к сумме всех частот ряда  единицу и результат разделим пополам, т.е. Медианным значением зарплаты будет то, которое составит полусумму зарплат 100-го и 101-го работников. Они попадают в четвертый интервал (10+20+58+65=153) по сумме накопленных частот, т.е. от 15 000 до 16 000 руб.  руб.Следовательно, половина работников имеют заработную плату не более 15 184,6 руб., а другая половина - не менее 15 184,6 руб. Для сопоставления структуры статистических совокупностей, сравнения фактических и нормативных структур, для количественной оценки динамических структурных изменений (структурных сдвигов) могут быть использованы показатели структурных различий. Обобщающую количественную оценку дают интегральные показатели структурных различий: интегральный коэффициент структурных различий (индекс Гатева): 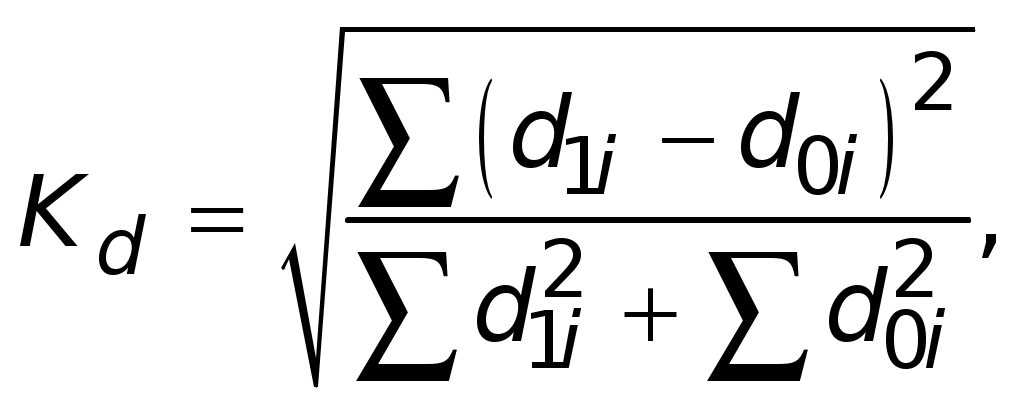 индекс Салаи: 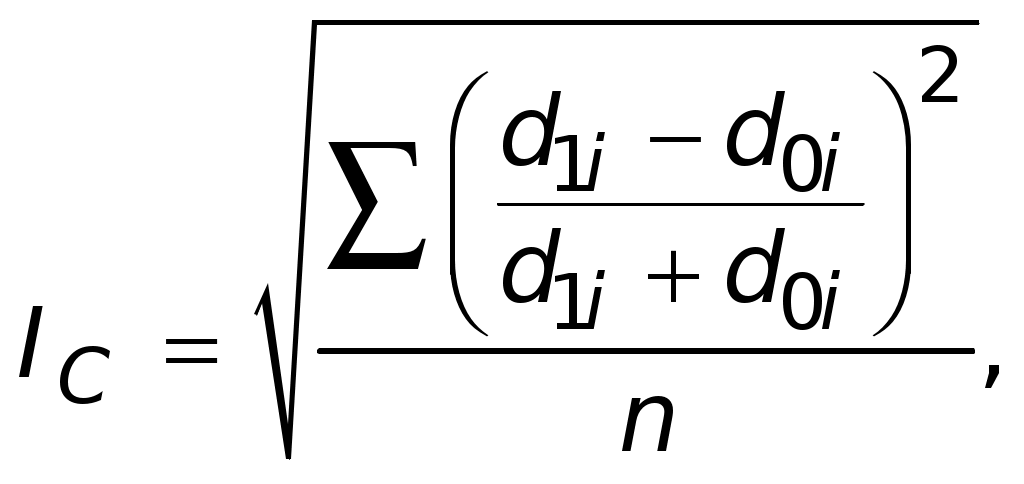 индекс В. Рябцева: 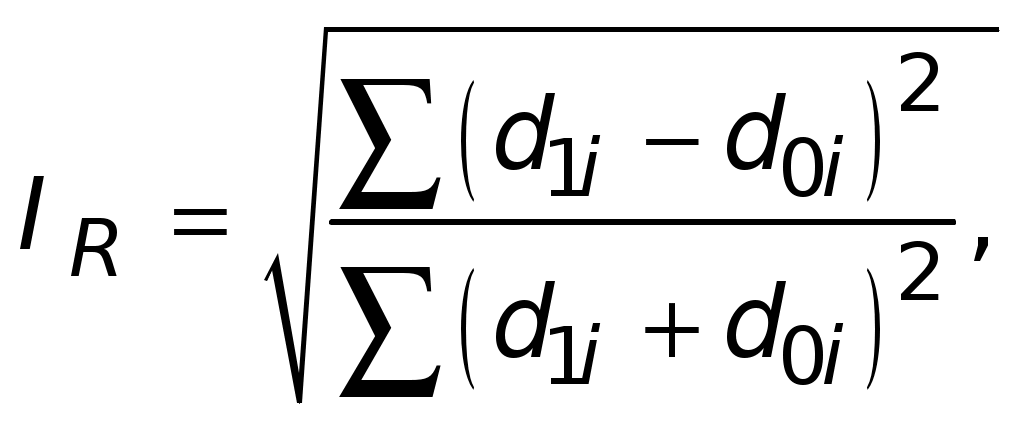 где d1i и d0i - сравниваемые структурные составляющие; n - число структурных градаций (выделенных групп). Приведенные показатели могут принимать значения от нуля до единицы. Минимальное нулевое значение показателей структурных различий свидетельствует о полной идентичности сравниваемых структур, их равенство единице соответствует максимально возможным различиям в структуре сравниваемых совокупностей. Для оценки меры структурных различий по критерию Рябцева разработана следующая шкала:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
