Методическая разработка по выполнению контрольной работы для студентов факультета второго высшего и дополнительного образования
 Скачать 1.29 Mb.
|
|
Пример решения задачи 6 I. Имеются следующие данные об остатках материалов на складе предприятия, тыс. руб.: на 1 января - 400; на 1 февраля - 455; на 1 марта - 465; на 1 апреля - 460. Определите среднемесячный остаток материалов на складе за I квартал. Решение По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда исчисляется по формуле средней хронологической простой: 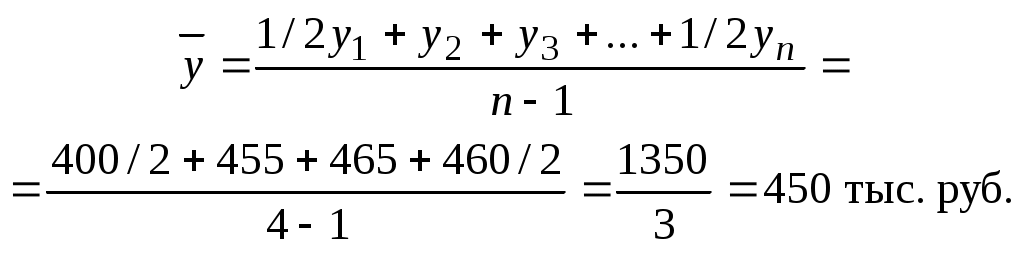 Среднемесячный остаток материалов на складе за I квартал составил 450 тыс. руб. II. Имеются следующие данные о товарных запасах розничного торгового предприятия, тыс. руб.: на 1 января 2008 г. - 61,1; на 1 мая 2008 г. - 57,5; на 1 августа 2008 г. - 51,3; на 1 января 2009 г. - 61,1. Вычислите среднегодовой запас розничного торгового предприятия за 2008 г. Решение Для моментного ряда динамики с неравными интервалами средний уровень ряда исчисляется по формуле средней хронологической взвешенной:  где  - средние уровни в интервале между датами; - величина интервала времени (число месяцев между моментами времени).В нашем примере число месяцев между моментами времени составило соответственно 4, 3, 5. Итак, средний уровень товарных запасов равен: 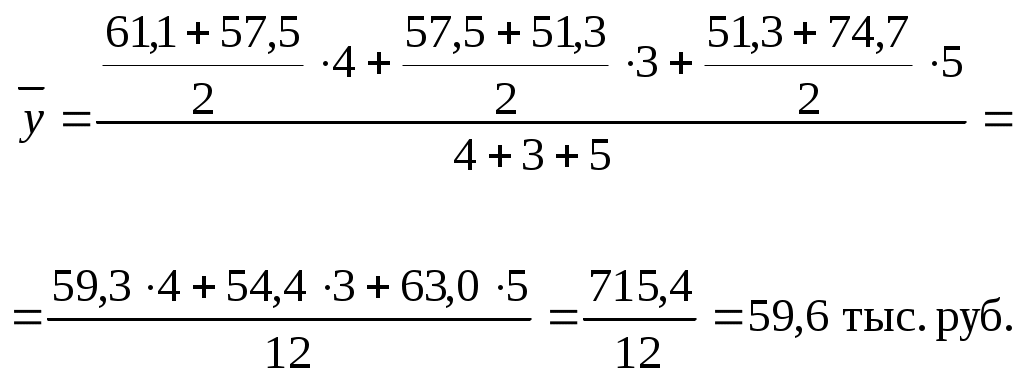 Задачи 7-8 охватывают один из наиболее сложных разделов теории статистики. Индексный метод анализа является одним из основных методов статистического изучения социально-экономических явлений. При выполнении заданий по этой теме необходимо понять сущность индексов (индивидуального и общего). Общие индексы могут исчисляться в агрегатной форме и как средние индексы (в средней арифметической и средней гармонической формах). Выбор формы индексов зависит от имеющихся исходных данных задачи. Индивидуальные индексы рассчитываются следующим образом: индивидуальные индексы цены:  ;индивидуальные индексы физического объема;  .Общие индексы в агрегатной форме: индекс цен  индекс физического объема  индекс стоимости (товарооборота)  Разность числителя и знаменателя индекса цен показывает дополнительные расходы населения при увеличении цен на товары и услуги или экономию у населения денежных средств в случае снижения цен. Индекс физического объема может быть представлен в средней арифметической форме:  Индекс цен может быть вычислен по средней гармонической формуле: 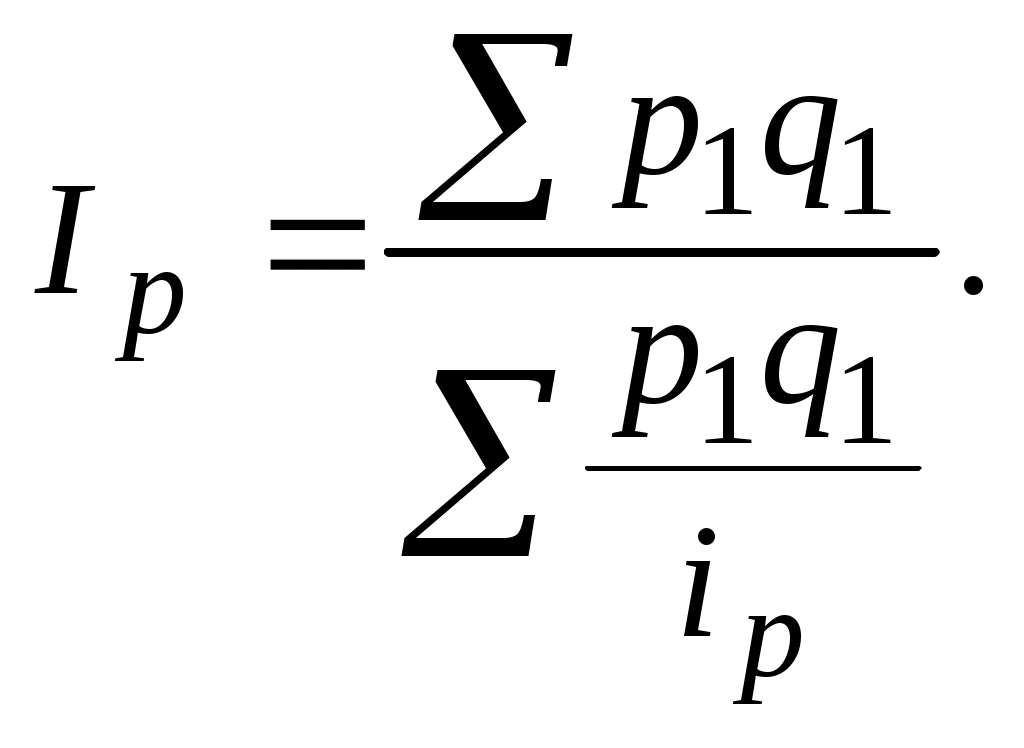 Индексный метод анализа позволяет также изучить динамику средней величины качественного показателя. Относительное изменение средней величины такого показателя (например, цены) называют индексом переменного состава:  Данный индекс отражает влияние двух факторов: 1) изменение индексируемого показателя у отдельных объектов (частей совокупности); 2) изменение удельного веса этих частей в общей совокупности (структурные сдвиги). Влияние первого фактора определяется с помощью индексов постоянного (фиксированного) состава:  Влияние второго фактора - с помощью индекса влияния структурных сдвигов:  При вычислении индексов можно использовать системы взаимосвязанных индексов: 1) товарооборота:   2) переменного состава, постоянного (фиксированного) состава и структурных сдвигов:  На основе данных систем по двум известным индексам исчисляется третий (неизвестный) индекс и выполняется факторный анализ изменений товарооборота (1) и среднего показателя (2). Пример решения задачи 7 I. Имеются следующие данные о продаже товаров в магазине за два квартала года:
Вычислите: 1) общий индекс товарооборота; 2) общий индекс физического объема товарооборота; 3) общий индекс цен. Решение 1. Общий индекс товарооборота равен:  Товарооборот во II квартале по сравнению с I кварталом вырос на 6,6%. Абсолютный прирост товарооборота составил 90 тыс. руб. (1460-1370). 2. Общий индекс физического объема товарооборота вычислим по формуле среднего арифметического индекса, который тождествен агрегатной форме индекса:  Для вычисления данного индекса определим предварительно индивидуальные индексы количества проданного товара: для овощей: 100-20=80%, или 0,80 (  );для мясопродуктов: 100+10=110%, или 1,10 (  );для масла растительного: 100%, или 1 (  ). т.е. физический объем товарооборота в среднем снизился на 5,7%. В результате изменения физического объема продаж товарооборот уменьшился на 78 тыс. руб. (1292-1370). 3. Общий индекс цен может быть исчислен с помощью взаимосвязи индексов:  Следовательно,  или 110,3%, т.е. цены в среднем возросли на 10,3%. За счет роста цен товарооборот увеличился на 168 тыс. руб. (1460-1292).II. Имеются следующие данные о продаже обуви в магазине города:
Определите изменение цен на проданную обувь в IV квартале по сравнению с III кварталом. Решение Общий индекс цен вычисляем по формуле среднего гармонического индекса, тождественного агрегатной форме индекса: 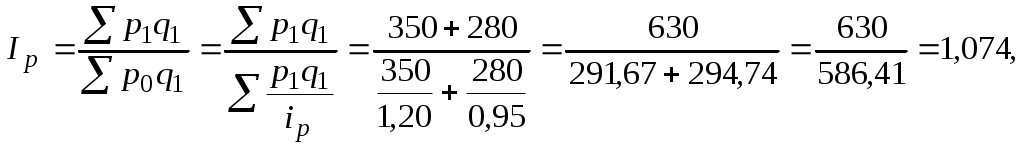 или 107,4%. То есть цены в среднем возросли на 7,4%. Пример решения задачи 8 Имеются следующие данные о выпуске продукции "А" по двум заводам:
Вычислите индексы себестоимости переменного, постоянного состава и влияния структурных сдвигов. Решение Вычислим индекс себестоимости переменного состава, который характеризует динамику средней себестоимости по двум заводам:  Средняя себестоимость продукции по двум заводам в отчетном и базисном периодах равна:   Следовательно, индекс себестоимости переменного состава равен:  Индекс показывает, что средняя себестоимость изделия по двум заводам снизилась на 14,5%. Это снижение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры производства продукции (удельного веса продукции отдельных заводов). Влияние первого фактора на динамику средней себестоимости выявим с помощью индекса себестоимости постоянного состава:  Себестоимость продукции по двум заводам в среднем снизилась на 13%. Влияние второго фактора характеризуется индексом структурных сдвигов: 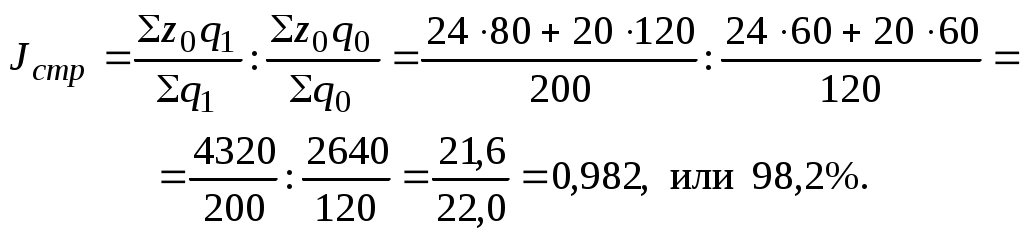 Средняя себестоимость изделия в отчетном периоде снизилась дополнительно на 1,8% за счет изменения структуры производства, т.е. за счет увеличения доли продукции второго завода с более низкой себестоимостью продукции с 50 до 60%. ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ Вариант 1 Задача 1 Имеются следующие данные по совокупности предприятий:
С целью изучения зависимости между численностью работников и объемом выпускаемой продукции произведите группировку предприятий по численности работников, выделив пять групп с равными интервалами; по каждой группе и в целом по совокупности подсчитайте: а) число предприятий; б) среднесписочную численность работников - всего и в среднем на одно предприятие; в) объем продукции - всего и в среднем на одно предприятие. Полученные результаты представьте в виде групповой таблицы. Сделайте выводы. Задача 2 По плану объем продаж АО в 2009 г. должен увеличиться на 5 млн. руб. Фактически объем продаж в сопоставимых ценах вырос по сравнению с 2008 г. на 5,5% и составил 146 млн. руб. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||