Методическая разработка по выполнению контрольной работы для студентов факультета второго высшего и дополнительного образования
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
Пример решения задачи 4 Имеются следующие условные данные о структуре денежных доходов населения региона, %:
Сделайте вывод об изменениях в структуре денежных доходов населения. Решение По приведенным показателям можно сделать вывод, что в составе денежных доходов населения доля оплаты труда снизилась (с 60% в базисном периоде до 42% - в отчетном) при увеличении удельного веса доходов от собственности и предпринимательской деятельности (соответственно, с 24 до 44%). Обобщающую характеристику меры структурных изменений дают интегральные показатели структурных различий, расчет которых проиллюстрируем в таблице:
Интегральный коэффициент структурных различий: 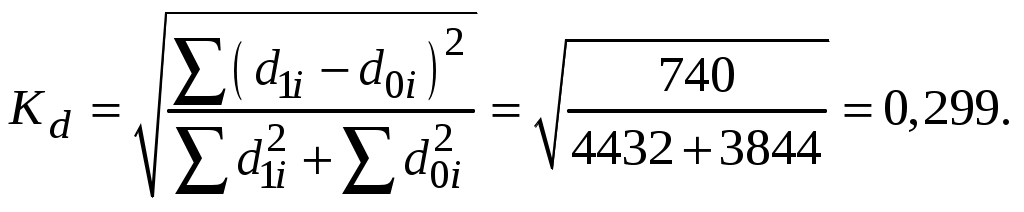 Индекс Салаи: 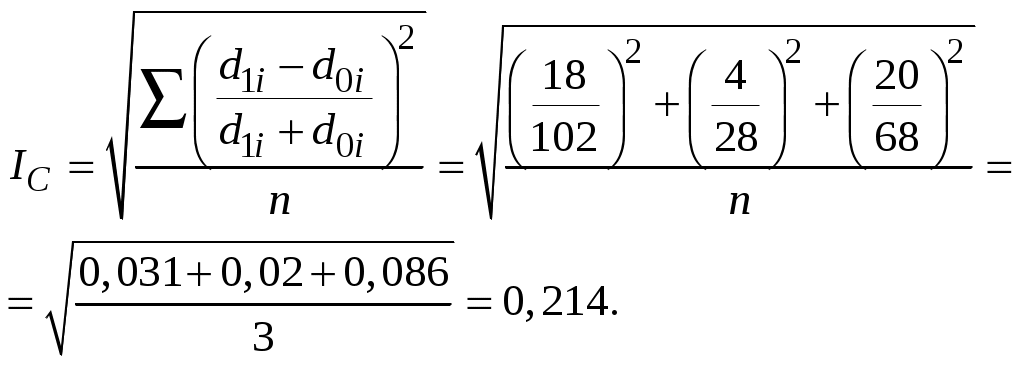 Индекс В. Рябцева: 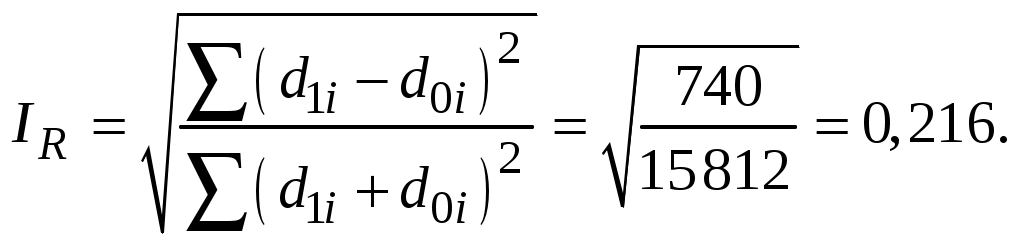 Величина исчисленных показателей структурных различий свидетельствует о существенных изменениях в структуре денежных доходов населения региона. Задачи 5-6 предполагают исследование динамики показателей, т.е. интенсивности изменения явлений во времени, которые осуществляются с помощью следующих индикаторов: абсолютных приростов, темпов роста, темпов прироста, абсолютного значения одного процента прироста, а также средних обобщающих показателей. В зависимости от задачи исследования показатели могут быть исчислены с переменной базой сравнения (цепные) и с постоянной базой сравнения (базисные). 1. Абсолютный прирост - это разность между сравниваемым уровнем и предыдущим или базисным: цепной абсолютный прирост: базисный абсолютный прирост: Сумма цепных абсолютных приростов равна базисному абсолютному приросту за соответствующий период времени. 2. Темп роста - относительный показатель, характеризующий интенсивность развития явления; он равен отношению изучаемого уровня к предыдущему или базисному и выражается в коэффициентах или процентах: цепной темп роста: базисный темп роста: Произведение соответствующих цепных темпов роста, исчисленных в коэффициентах, равно базисному. 3. Темп прироста определяют двумя способами: а) как отношение абсолютного прироста к предыдущему уровню (цепной) или базисному уровню (базисный): цепной темп прироста: базисный темп прироста: б) как разность между темпом роста и 100%: 4. Абсолютное значение одного процента прироста определяется как отношение цепного абсолютного прироста к цепному темпу прироста (%) или для каждого последующего уровня - как 0,01 предыдущего уровня ряда динамики: 5. Средний абсолютный прирост вычисляется по средней арифметической простой, т.е. делением суммы цепных абсолютных приростов на их число: Средний темп роста находят по формуле средней геометрической: Средний темп прироста находят путем вычитания из среднего темпа роста 100%: Методы расчета среднего уровня ряда динамики зависят от его вида и полноты информации: 1) в интервальных рядах с равными интервалами времени средний уровень определяется по формуле средней арифметической простой; 2) в интервальных рядах с неравными интервалами времени - по формуле средней арифметической взвешенной (по величине интервалов); 3) в моментных рядах с исчерпывающими данными об изменении моментного показателя расчет производится по средней арифметической из уровней ряда, сохранявшихся неизменными в течение определенных промежутков времени, взвешенной по величине соответствующих промежутков; 4) в моментных рядах динамики с равноотстоящими уровнями применяется формула средней хронологической простой; 5) в моментных рядах динамики с неравными промежутками времени между уровнями - средняя хронологическая взвешенная. Пример решения задачи 5 Имеются следующие данные о производстве продукции предприятия за 6 лет (в сопоставимых ценах, млн. руб.):
Рассчитайте: 1) цепные и базисные абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста; 2) среднегодовые значения абсолютного прироста, темпа роста и прироста; 3) средний уровень ряда динамики. Решение 1. Абсолютные приросты
Сумма цепных абсолютных приростов равна базисному абсолютному приросту для любого года. Так, для 2008 г.: 0,4 + 0,5 + 0,6 + 0,6 + 0,7 = 2,8. Коэффициенты (темпы) роста
Произведение цепных коэффициентов роста равно базисному коэффициенту роста. Для 2008 г.: 1,050 · 1,059 · 1,067 · 1,063 · 1,069 = 1,350. Коэффициенты (темпы) прироста
Абсолютное значение одного процента прироста
Исчисленные выше аналитические показатели ряда динамики представлены в таблице. Динамика производства продукции предприятия за 2003-2008 гг.
2. Среднегодовой абсолютный прирост: или Среднегодовой темп роста: или Среднегодовой темп прироста; 3. Средний уровень ряда динамики находим по формуле средней арифметической простой, так как представленный ряд - интервальный с равными интервалами времени (один год): Таким образом, производство продукции на предприятии ежегодно возрастало. За 2003-2008 гг. абсолютный прирост составил 2,8 млн. руб. Темп роста за этот период составил 135%, темп прироста - 35%. В среднем за год абсолютный прирост составил 0,56 млн. руб., а среднегодовой темп прироста - 6,2%, т.е. производство продукции ежегодно увеличивалось в среднем на 0,56 млн. руб., или на 6,2%. Значение 1% прироста также возросло с 80 до 101 тыс. руб. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
