Главный Учебник. Главный учебник МММ. Методические материалы по курсу экономикоматематическое моделирование
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Варианты заданий по теме 2Вариант 1 Задача 1. Решить графическим методом следующую ЗЛП: Z = x1 - 3x2 → max x1 – x2 ≤ 3 2x1 + x2 ≥ 3 x1 – 3x2 ≤ 1 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = x1 + 3x2 + x3 → ––max -x1 + x2 + x3 ≤ 1 x1 + x2 + x3 ≤ 4 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 2 Задача 1. Решить графическим методом следующую ЗЛП: Z = 3x1 + 5x2 → max x1 + x2 ≤ 5 3x1 – x2 ≤ 3 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом Z = 4x1 + 3x2 → max -x1 + 3x2 ≤ 9 2x1 + 3x2 ≤ 18 2x1 – x2 ≤ 10 x1 ≥0, x2 ≥0 Вариант 3 Задача 1. Решить графическим методом следующую ЗЛП: Z = 2x1 + 2x2 → min x1 + 3x2 ≥ 3 -2x1 + x2 ≤ 2 x1 + x2 ≤ 5 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом Z = 2x1 + x2 + 2x3 → max 3x1 + 2x2 + x3 ≤ 6 x1 + x2 + 2 x3 ≤ 4 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 4 Задача 1. Решить графическим методом следующую ЗЛП: Z = 2x1 + 2x2 → max x1 + 3x2 ≥ 3 -2x1 + x2 ≤ 2 x1 + x2 ≤ 5 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = 5x1 + 4x2 - x3 → max x1 – 2x2 + 2x3 ≤ 20 x1 + 4x2 – x3 ≤ 16 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 5 Задача 1. Решить графическим методом следующую ЗЛП: Z = 2x1 + 3x2 → min x1 + x2 ≤ 4 6x1 + 2x2 ≥ 6 x1 + 5x2 ≥ 5 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = 4x1 - x2 + x3 → max x1 + 2x2 + x3 ≤ 20 2x1 – x2 + 2 x3 ≤ 10 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 6 Задача 1. Решить графическим методом следующую ЗЛП: Z = –2x1 + x2 → min x1 – x2 ≤ 3 x1 + x2 ≤ 9 -x1 + x2 ≥ 3 x1 + x2 ≥ 3/2 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = 3x1 + 5x2 → min x1 + x2 ≤ 5 3x1 – x2 ≤ 3 x1 ≥0, x2 ≥0 Вариант 7 Задача 1. Решить графическим методом следующую ЗЛП: Z = 4x1 + 3x2 → max -x1 + 3x2 ≤ 9 2x1 + 3x2 ≤ 18 2x1 – x2 ≤ 10 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = 3x1 + x2 + 3x3 → max x1 + 3x2 + 5x3 ≤ 9 2x1 + 2x2 + x3 ≤ 5 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 8 Задача 1. Решить графическим методом следующую ЗЛП: Z = x1 + x2 → max -x1 + x2 ≤ 1 x1 + 2x2 ≤ 10 x1 + 2x2 ≥ 2 2x1 + x2 ≤ 10 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = x1 + x2 + x3 → max 2x1 + x2 + x3 ≤ 2 4x1 + 2x2 + x3 ≤ 2 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 9 Задача 1. Решить графическим методом следующую ЗЛП: Z = 3x1 + 5x2 → min x1 + x2 ≤ 5 3x1 – x2 ≤ 3 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом Z = 5x1 + 4x2 + x3 → max x1 + 4x2 + 2x3 ≤ 8 2x1 + x2 + x3 ≤ 4 x1 ≥0, x2 ≥0, x3 ≥0 Вариант 10 Задача 1. Решить графическим методом следующую ЗЛП: Z = 2x1 + x2 → max x1 + x2 ≤ 8 3x1 – 2x2 ≤ 12 -x1 + 2x2 ≤ 8 2x1 + 3x2 ≥ 6 x1 ≥0, x2 ≥0 Задача 2. Решить ЗЛП симплексным методом. Z = 2x1 + x2 + x3 → max x1 + x2 + x3 ≤ 6 2x1 - x2 + x3 ≤ 2 x1 ≥0, x2 ≥0, x3 ≥0 Тема 3. Двойственная задача линейного программирования Пример задачи. По исходной задаче требуется построить двойственную. Исходная задача: L = 10x1 + 6x2 – 4x3 →max 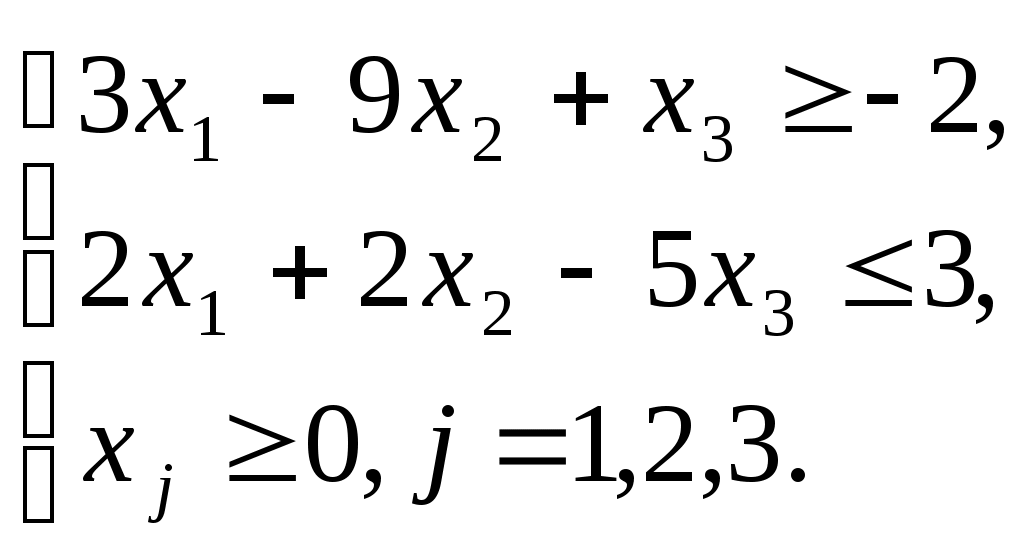 Решение задачи: Приведем все неравенства системы ограничений исходной задачи к одному знаку: 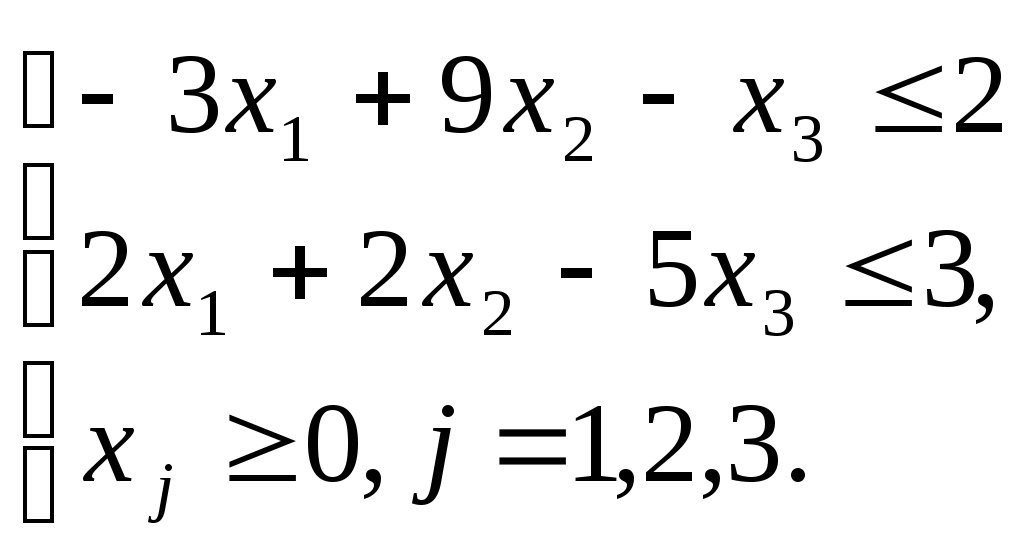 Двойственная задача. 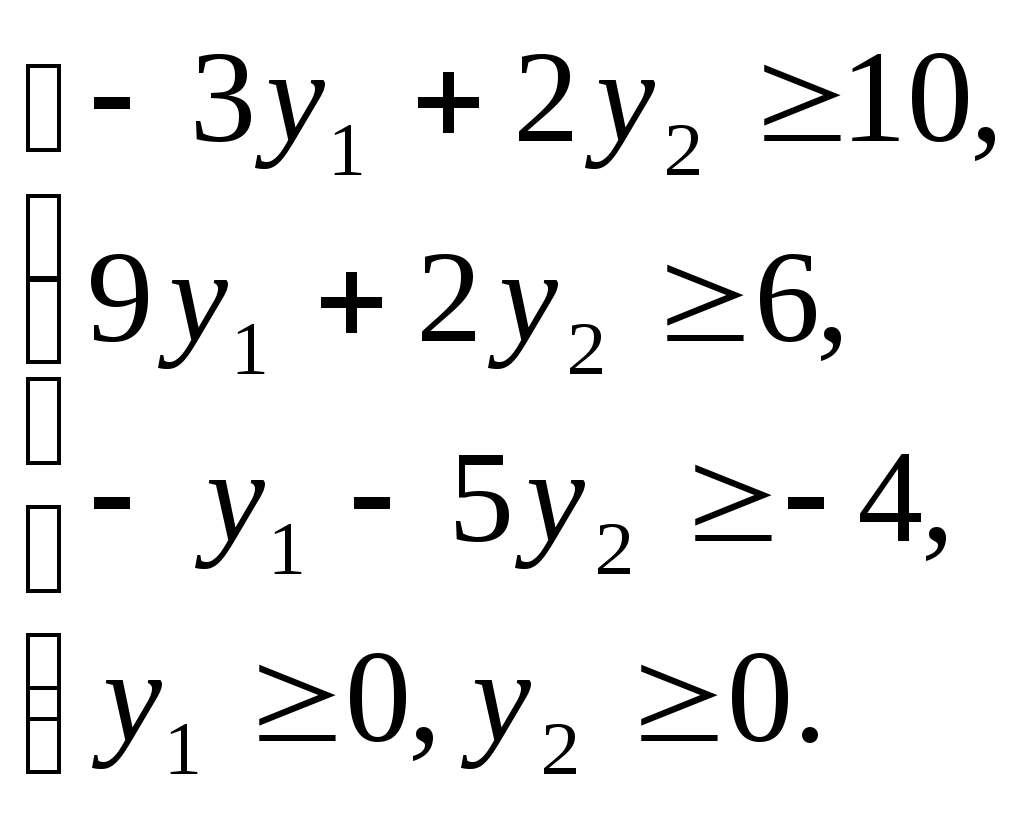 |
