Методичка к экзаменам_магистратура. Методические материалы по написанию вступительного теста в магистратуру вшфм. Раздел Финансовая математика. Индексы, доходности
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Раздел 6. Теория портфеля (доходность, риски, беты и т.д.). Поскольку портфель состоит из нескольких активов с разными характеристиками, то доходность всего портфеля следует рассчитывать как средневзвешенную по долям инвестиций в каждый актив:  (2.0) 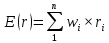 Изменяя доли инвестиций можно менять итоговую доходность в достаточно широких пределах, причем эти пределы не ограничиваются доходностями обеих активов. Это связано с тем, что актив может иметь нулевой вес (в актив ничего не инвестировано), отрицательный вес (по активу осуществлена короткая продажа), вес больше единицы (актив куплен на заемные средства). Именно такая возможность позволяет инвестору конструировать некий синтетический актив с очень широким спектром показателей.  Продажа без покрытия (англ. short selling) —короткая продажа, шорт. Продажа актива, которым торговец в настоящее время не владеет. Предполагает в дальнейшем возврат кредита в натуральном (товарном) виде. Доли инвестиций - веса активов принято обозначать буквой w. Очевидно соотношение:  (2.1) 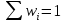 Задача 6.1. Пусть существует портфель из двух активов А и В со следующими параметрами: Общая сумма инвестиций = $300 000; Сумма инвестиций в актив А = $210000. Найти веса инвестиций в каждый из активов.
Задача 6.2. Пусть существует портфель состоящий из активов А и В со следующими параметрами: Общая сумма инвестиций = $300 000. Инвестор увеличил актив А на $120 000 используя короткую позицию. Найти вес актива А.
Задача 6.3. Найти доходности портфеля в задачах №12 и № 13, если доходности активов А и В равны 12% и 8% соответственно.
Особое место в теории портфеля занимает портфель состоящий из рискового (такой актив может быть и синтетическим) и безрискового актива, при этом под рисковым активом понимают актив с дисперсией матожидания больше нуля. а под безрисковым - актив с нулевой дисперсией. Такой портфель носит имя своего создателя - Гарри Марковица и является базовым для всей дальнейшей теории портфеля. Если вес рисковой части выразить через w, доходность безрисковой части чрез rf , а доходность рисковой части через E(r) , то тогда доходность портфеля будет рассчитываться в соответствии с формулой:  (3.0) E(rр) = rf + w[E(r) - rf] а стандартное отклонение портфеля:  (3.1) σр = w×σ Задача 6.4. Пусть рисковый портфель имеет следующие параметры: E(r) = 15%; σp = 22%; rF = 7%. Доля инвестиций в рисковую часть равна 0,7. Рассчитать доходность и СКО портфеля.
Задача 6.5. Постройте на графике с осями E(r) и σ график, описывающий портфель приведенный в задаче № 6.4. Прокомментируйте графический смысл выражения S = (E(rp) - rF)/ σp Решение:  Рисунок 1. Прямая SML  Пусть у нас есть портфель, состоящий из рискового и безрискового актива. Меняя вес (долю) рискового актива в портфеле, мы получим бесконечное множество портфелей лежащих на одной линии. Рисунок №1 отражает соотношение между ожидаемой ставкой доходности и стандартным отклонением. Мы можем рассчитать параметры прямой, указанной на рисунке, используя соотношении (3.0) заменив в нем w на σр/σr , что следует из (3.1). Тогда:  (3.2) 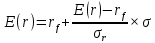 Используя каноническую запись уравнения прямой в декартовых координатах:  (3.3) Y(x) = a + bx выражение стоящее перед параметром σ и отражающее наклон прямой называется коэффициентом Шарпа  (3.4) 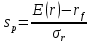  (3.5) окончательно имеем: E(r) = rf+ Sp×σ Задача 6.6. Почему в соотношении (3.4) коэффициент Шарпа имеет индекс «р» (портфель), если для расчета используется стандартное отклонение только рискового актив?
Задача 6.7. Может ли коэффициент Шарпа при любой комбинации рискового и безрискового активов отличаться от коэффициента применяемого только для портфеля состоящего исключительно из рискового актива?
Задача 6.8. Пусть рисковый портфель имеет следующие параметры: E(r) = 15%; σp = 22%; rF = 7%. . Что произойдет с коэффициентом Шарпа, если инвестор увеличит рисковые активы на $120 000 используя короткую позицию.
Задача 6.9. Почему коэффициент Шарпа не меняется при короткой покупке рискового актива в кредит? Что произойдет с коэффициентом Шарпа, если кредит будет взят по ставку более высокую. чем безрисоквая?
§3.2. Портфели из двух рисковых активов. Давайте добавим к рисковому активу 1 рисковый актив 2 и рассмотрим получившийся портфель. Тогда ожидаемая доходность такого портфеля будет (w - доля актива 1):  (3.6) E(rр) = wE(r1) + (1-w)E(r2)  (3.7) а среднее квадратичное отклонение: σ2 = w2σ12 + (1-w)2σ22 + 2w(1-w)ρ1;2σ1σ2 Представленные уравнения (3.6) и (3.7) по сути более общий вид уравнений (3.0) и (3.1). Тогда все портфели состоящие из этих двух рисковых активов будут лежать на кривой между точками PR и R2. Эта линия не прямая (тогда ее просто невозможно было бы оптимизировать, но, в соответствии с формулой (3.7) является некоторой кривой (Смотри рисунок №3). Из рисунка видно. что: 1. Появляется некая точка характеризующая портфель с минимальным уровнем риска (точка О); 2. Появляется область кривой (между точками Е и R1) представляющей портфели эффективность которых выше, чем портфель составленный из одного актива R1. Точка минимального риска (точка О на рисунке 3) находится обычными методами нахождения экстремума.  Задача 6.10. Вывести формулу веса одного из рисковых активов при котором дисперсия минимальна. (Найти точку О. Рисунок № 3)
Задача 6.11. Заполнить таблицу, коэффициент корреляции между активами (ρ ) принять равным 0.
Задача 6.12. Определить среднюю ожидаемую доходность и ее стандартное отклонение для портфеля состоящего из рисковых активов 1 и 2 описанных в таблице задачи № 6.11, в котором доля рискового актива 1 составляет 60%, а коэффициент корреляции между рисковыми активам равен 0,1?
В качестве всеобъемлющего индекса ценных бумаг часто принимают индекс различных бирж (например S&P 500) и рассматривают ковариацию активов входящих в портфель через такой индекс. В связи с тем, что в качестве всеобъемлющего индекса принимается индекс одной биржи, то такая модель получила название одноиндексной модели. Поскольку норма доходности в индексной модели ri = αi + βimrm + εi, то рассчитаем доходность актива: Рассчитаем доходность актива используя рыночную модель. Из уравнения регрессии имеем:  (6.8) Е(ri) = Е(αi) + βim Е(rI) + Е(εi) Поскольку αi – константа, то Е(αi) = αi; Е(εi) = 0 (по определению) то имеем:  (6.9) Е(ri) = αi + βim Е(rm) Индексная модель дает систематическую и специфическую составляющие общего риска каждой ценной бумаги, а также ковариацию между любой парой ценных бумаг:  (6.10) 1. Общий риск = Систематический + Особый (уникальный) риск компании (ничто иное, как формула (6.5)) σ2i = β2im σ2m + σ2(εi) 2. Ковариация равна = Произведение показателей беты (βi и βj) × риск рыночного индекса  (6.11) Cov(ri,rj) = βiβjσ2m 3. Корреляция = Произведение коэффициентов корреляции ценных бумаг с рыночным индексом:  (6.12) ρij = βiβjσ2m / σiσj = β2iσ2mβ2jσ2m / σiσmσjσm = ρim × ρjm Задача 6.13. Следующие данные описывают финансовый рынок, состоящий из трех акций и удовлетворяющий одноиндексной модели:
СКО рынка равно 25% а) Чему равна средняя α? б) Чему равна Cov(A,B)? в) Чему равна Cov(B,I) г) Разбейте дисперсию акции В на ее систематическую и специфическую (фирменную) составляющие.
Задача 6.14. Допустим, что индексная модель для расчета избыточной доходности акций А и В оценивается следующим образом: RA = 1,0% + 0,9RM +eA RB = -2,0% + 1,1RM + eB σm = 20% σ(eА) = 30% σ(eВ) = 10% Найдите СКО каждой акции и ковариацию между ними.
Задача 6.15. используем данные задачи №18. Предположим, что мы формируем равновзвешенный портфель из акций А и В. Каково несистематическое среднее квадратическое отклонение такого портфеля?
Задача 6.16. Пусть премии за риск рыночного портфеля оцениваются в 8% при СКО 22%. Какова премия за риск портфеля инвестированного на 25% в акции GM, и на 75% в акции Ford, если их показатели "бета" равны 1,1 и 1,25 соответственно?
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||