Методичка к экзаменам_магистратура. Методические материалы по написанию вступительного теста в магистратуру вшфм. Раздел Финансовая математика. Индексы, доходности
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Методические материалы по написанию вступительного теста в магистратуру ВШФМ. Раздел 1. Финансовая математика. Индексы, доходности. Ключевые соотношения для расчета доходности актива. Пусть существует изменение некоторого фактора во времени. Не вникая в то, по каким законам происходит это изменение, попытаемся ответить на следующие вопросы: 1. Как можно сравнить изменения одного и того же фактора за различные периоды; 2. Как можно сравнить изменения разных факторов за один и тот же промежуток времени. Математика знает всего два метода сравнения разных величин: 1). Вычитание одной величины из другой и анализ знака полученного результата. Если мы сравниваем величины А и Б, то если А - Б > 0, то мы говорим о том, что величина А больше величины Б (А>Б) и наоборот. 2). Деление одной величины на другую и сравнение полученного результата с единицей. Сравнивая величины А и Б этим способом имеем: если А/Б > 1, то А>Б. Если А/Б<1, то А<Б. При расчете доходности используются следующие ключевые соотношения: I. Прирост ценности актива за время владения. 1. Рассчитывается как разница между текущей и первоначальной значением измеряемой величины:  Прирост ценности актива = Цена продажи - Цена покупки или, в виде формулы: ΔV = Vt - V0  (1.1.0) 2. Показатель, характеризующий абсолютное изменение измеряемой величины и отвечающий на вопрос: "На сколько?"; 3. Имеет размерность; 4. Может иметь как положительное, так и отрицательное значение; 5. Показатель можно только складывать или вычитать. Если мы рассматриваем изменение ценности какого либо актива, мы будем называть абсолютный прирост доходом при положительном значении и убытками при отрицательном значении прироста. II. Рост ценности актива (индекс, индекс роста). 1. Рассчитывается как отношение текущей к первоначальной цене актива:  Рост ценности актива = Цена продажи / Цена покупки или, в виде формулы: 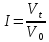  (1.1.1) 2. Показатель, характеризующий изменение измеряемой величины и отвечающий на вопрос: "Во сколько раз?"; 3. Не имеет размерности. Измеряется либо в долях единицы, либо в процентах. Для расчета в процентах индекс необходимо умножить на 100%. ; 4. В числителе и знаменателе стоит одна и та же величина отличающаяся либо временем, либо местом. Может иметь только положительное значение. 5. Показатель можно только умножать или делить. III. Относительный прирост ценности актива (инвестиций). 1. Рассчитывается как отношение абсолютного прироста к первоначальному вложению. Может иметь как положительное, так и отрицательное значение.  Относительный прирост = (Цена продажи - Цена покупки) / Цена покупки или, в виде формулы: 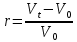  (1.1.2) 2. Показатель, характеризующий относительное изменение измеряемой величины и отвечающий на вопрос: "На сколько процентов?"; 3. Не имеет размерности. Измеряется либо в долях единицы, либо в процентах. Для расчета в процентах индекс необходимо умножить на 100%; 4. Может иметь как положительное, так и отрицательное значение; 5. Показатель можно только складывать или вычитать. Эти соотношения справедливы как для активов по которым производятся выплаты за время их владения (акции по которым выплачиваются дивиденды, облигации с купонным выплатам и т.д.), так и для активов, по которым подобные выплаты отсутствуют (векселя, депозиты в банке, бескупонные облигации. сертификаты на драгметаллы и т.д.), но если в первом случае в текущую ценность Vt эти выплаты включаются, то во втором - текущая ценность отражает только ценность актива на момент окончания периода владения. Используя соотношения (1.1.1) и (1.1.2) можно легко получить из индекса доходность и наоборот:  (1.1.3) I -1 = r или I = 1+r Соотношения (1.1.0), (1.1.1), (1.1.2) справедливы не только для активов формирующих свою доходность на момент окончания владения, но активов приносящих дополнительные выгоды в течении периода владения - отличия только в смысле ценности актива на момент окончания владения. Необходимо сделать два важных замечания: Первое: формула (1.1.3) очень важна, поскольку позволяет связать индекс роста и относительный прирост простым соотношением: зная относительный прирост индекс получаем простым прибавлением единицы. Если относительный прирост дан в процентах, то следует прибавить 100%. Второе: в данной формуле рассматривается относительный прирост только за один период времени. Если было несколько периодов времени, то расчеты ведутся по каждому периоду отдельно. Задача 1.1. Инвестор приобрел 120 штук акций компании ART по цене $100 за штуку и продал их через некоторое время по цене $104 за штуку. Рассчитать доход операции, рост инвестиций и доходность операции.
Задача 1.2. Рассчитать рост инфляции (индекса цен) в 1996 году, если за год инфляция выросла на 420%. (Использовать соотношение описывающее связь между ростом и относительным приростом)
Задача 1.3. Рассчитать рост заработной платы за 2007 год, если на 31 декабря 2006 года средняя з/п составляла 12 500 руб., а на 31 декабря 2007 года 14 600 руб.
§1.2. Расчет доходности за несколько периодов. Приведение индекса и доходности к годовому показателю. Если есть несколько периодов инвестиций с известным индексом роста, то итоговый индекс роста - за все периоды владения - рассчитывается не как сумма индексов за эти периоды (поскольку индексы мультипликативные, а не аддитивны показатели), а как произведение этих индексов. Если индексы за каждый период равны, то результирующий индекс за n периодов рассчитывается как:  (1.2.0) Iрез. = Iin Если необходимо рассчитать рост показателя за несколько периодов, причем каждый характеризуется своими темпами роста, то итоговый индекс находится как произведение индексов отражающих изменение показателя за каждый период, т.е.  (1.2.1) Iрез. = I1×I2×...×In  (1.2.2) Из формулы расчета индекса за несколько периодов следует, что средний рост за несколько периодов находится как среднее геометрическое. 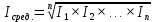 Не обладает аддитивностью и относительный прирост (доходность). Поэтому доходность за несколько периодов рассчитывается через индекс роста: 1. Для каждого периода рассчитывается индекс роста (прибавляем единицу к доходности); 2. Рассчитывается итоговый индекс роста (формула (1.2.0) или (1.2.1)); 3. Находим итоговую доходность за весь период (отнимаем единицу от индекса роста). Задача 1.4 . Акции купили по цене $ 100 за акцию. В конце первой торговой сессии цена за акцию была $ 95 , а в конце второй - $ 102. Рассчитать итоговую доходность купленных акций используя: а) определение доходности; б) используя для расчета итоговый индекс. Что произойдет, если для поиска ответа просто сложить доходности за первую и вторую сессии?
Формулы (1.2.0) (1.2.1) используется также для приведения доходности и индекса роста инвестиций к "годовому" периоду, т.е. к доходностям и индексам роста рассчитанных за период равный году. Это делаются потому, что время владения активом может не совпадать с периодом в один год, а для сравнения привлекательности различных активов периоды владения активом должны быть одинаковыми. Задача 1.5. Доходность операций торговой компании за первое полугодие представлено в таблице. Рассчитать годовую доходность этой компании при условии, что доходность за первое полугодие будет равна доходности за второе полугодие. Ответ округлить до десятых долей процента.
Задача 1.6. Инвестор приобрел 210 штук акций компании LST по цене $100 за штуку и продал их через некоторое время по цене $106 за штуку. Рассчитать доходность операции в годовых, если период владения акциями составил: а) 3 месяца; б) четыре месяца; в) 9 месяцев.
Задача 1.7. Имеются следующие данные по динамике потребительских цен в РФ с января по июнь отчетного года:
Определите: а) как изменились потребительские цены в 1-ом квартале; б) как изменились потребительские цены в 2-ом квартале; в) как изменились потребительские цены за полугодие в целом; г) среднемесячное изменений потребительских цен; д) годовую инфляцию.
Для сравнения доходности различных активов достаточно сравнить их индексы, а не рассматривать весь пакет. При этом необходимо помнить, что индексы нельзя складывать и вычитать, а можно только умножать и делить. Задача 1.8. Акции компании Ford покупались за $80,5, а были проданы за $86,5; акции компании GM были куплены $23,5 и проданы за $25,5. Какие акции доходней и насколько?
Еще одно следствие расчета средней доходности через среднее геометрическое: если четное количество периодов доходность росла, а четное - падала на один и тот же процент, то средняя доходность за период не равна нулю. Задача 1.9. Четыре периода равны по продолжительности. Доходность инвестиций в первый и второй периоды росли на 10%, а в третий и четвертый - падали на такой же процент. Рассчитать среднюю доходность за период.
Задача 1.10. Фотографию уменьшили на 20%. На сколько надо увеличить фотографию, чтобы вернуть ей первоначальный размер?
Средневзвешенная доходность. Пусть нам необходимо рассчитать доходность акций некой компании за одну торговую сессию. В период сессии мы покупали и продавали акции компании различными лотами (объемами акций) и каждый лот имел свои показатели доходности. Даже если рассчитывать доходность от владения каждым лотом в отдельности, все равно нам необходимо иметь правило, которое позволило бы рассчитать итоговую доходность от владения всеми лотами данного актива. Как поступить в таком случае - как рассчитать доходность всех операций по покупке и продаже данного актива? На данные вопросы дает ответ расчет средневзвешенный доходности. Если актив покупался и продавался частями с разными доходностями, то если принять всю сумму инвестиций за единицу, а потом рассчитать доли инвестиций с равными доходностями, то искомую доходность можно получить по следующей формуле, называемой формулой средневзвешенной доходности:  (1.3.0) Δrср.вз. =(w1×r1+w2×r2+...+wn×rn) где r1, r2, ... ri - доходности каждой доли инвестиций; w1 ,w2 , ...wi - показатель, относительно которого "взвешиваются" доходности. Задача 1.11. Инвестор формирует равновзвешенный портфель состоящий из четырех активов с годовыми доходностями в 8,2%; 8,8%; 9,0 и 10,4% соответственно. Рассчитать годовую доходность портфеля.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
