Методичка к экзаменам_магистратура. Методические материалы по написанию вступительного теста в магистратуру вшфм. Раздел Финансовая математика. Индексы, доходности
 Скачать 0.53 Mb.
|
|
Раздел 2. Финансовая математика. Теория процента. 2.1.1 Процент.  Процент — это одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому. Финансовое определение процента - плата, которую одно лицо (заемщик) передает другому лицу (кредитору) за то, что последний предоставляет первому во временное пользование денежные средства.  Объем выплаченных (полученных) процентов зависит от следующих факторов: 1. Ставка процента. (интенсивность начисления процентов) 2. Срок пользования заемными средствами 3. Способ начисления (простой, сложный, непрерывно начисляемый процент) 4. Количество периодов начисления процента 5. Момент выплаты процентов. Различают декурсивные (postnumerando) проценты, которые выплачиваются в конце периодов финансовой операции и антисипативные (prenumerando) проценты, которые выплачиваются в начале финансовой операции. Задача 2.1. Рассчитать доходность кредита, если сумма ссуженных средств составляет 80 тыс. д.е., а полученная в итоге данной финансовой операции сумма составляет 104 тыс. д.е. Воспользоваться определением относительного прироста.
2.1.2. Простые проценты. Пусть ссуженная сумма равна PV (Present Value), ставка процента r годовых, срок выдачи кредита - n лет. Тогда, если проценты не прибавляются к основной сумме долга, полученная в будущем сумма FV (Future Value) будет равна:  (2.1.0) FV = PV+ PV×r1 + PV×r2 + PV×rn = PV×(1+nr) Если процент начислялся за время меньшее, чем период начисления процентов, то формула будет несколько иной:  (2.1.1) FV = PV(1+r×n/365) где r - процентная ставка за год, n - количество дней начисления. Такой метод расчета называется простыми процентами. Задача 2.2. Сколько нужно положить в Сбербанк 01.03.2015 под 16% годовых, чтобы к 17.09.2015 получить 10 000 руб.? Выполнить из расчета простых процентов, округлив до целых рублей в большую сторону:
2.1.3. Сложные проценты. Если мы берем в долг сумму PV, то через определенное время должны вернуть как саму сумму, так и проценты начисленные за пользование этой суммы. (2.1.2) FV = PV + PV×r = PV(1+r) Если периодов начисления процентов несколько, то сумма, которую мы должны вернуть рассчитывается как: (2.1.3) FV = PV(1+r)(1+r)...(1+r) = PV(1+r)n Такой метод расчета называется сложными процентами. Легко заметить, что r - это относительный прирост первоначальной суммы, тогда: (2.1.4) FV = PV×I где I = (1+r)- рост (индекс роста) первоначальной суммы за один период. Легко видеть, что данное выражение можно получить просто из определения роста:  (2.1.5) I = FV/PV Для нескольких период будущая сумма рассчитывается как: (2.1.6) FV = PV×I1×I2×...×In Если относительный прирост (процентная ставка r) за период одинакова, то формула превращается в (2.1.7) (2.1.7) FV = PV×In Задача 2.3. 31 декабря 1993 года мы положили в банк 1 000 000 руб. Какую сумму мы должны получить через три года, если депозитные ставки составляли соответственно 50%, 70% и 56,9% годовых в 1994, 1995 и 1996 годах.
Задача 2.4. Какую сумму мы получим через 20 лет, если 2,5 млн. положили под 7,2% годовых? Ответ округлить до ста тысяч (десятых долей миллиона).
2.1.4 Смешанные проценты. Если время депозита составило несколько полных периодов и неполный, то количество полных периодов начисления рассчитываются по формуле сложных процентов, а оставшаяся часть - по формуле простых процентов. Такой метод начисления носит название начисление смешанных процентов. Задача 2.5. Сколько нужно положить в Сбербанк 01.02.2015 под 18% годовых, чтобы к 15.09.2015 получить 10000 руб. из расчета сложных процентов с ежеквартальной капитализацией начиная с 01.02.2015? Выполнить расчеты, округлив до десятков рублей в большую сторону:
Задача 2.6. Вычислить по правилу смешанного процента средний процент с 1 июля 1998 года по 30 июня 2000 года, если капитализация процента совершалась раз в квартал, а процент годовых изменился два раза: с 25% до 21% 1 апреля 1999 года и 1 января 2000 года ставка процента уменьшилась на 5 процентных пунктов. Округлите ответ до сотых процента по обычным правилам математики.
2.1.5 Проценты с плавающей (переменной) ставкой Процентная ставка по депозиту (кредиту) определяется в момент подписания договора. Но, как это часто бывает, в процессе осуществления договора могут изменится некоторые макроэкономические показатели (ставка рефинансирования, инфляция, действия Регуляторов и т.д.) которые могут сделать процентную ставку договора невыгодной для сторон. В таком случае, применяется плавающая ставка, т.е. ставка не закрепленная в момент подписания договора, а изменяющаяся от периода к периоду. Задача 2.7. Найти среднюю процентную ставку, то есть процент, дающий тот же результат, что и следующая плавающая (переменная) ставка процента, составившая 18% в первый год, 10% - во второй, 21% - в третий и 12% - в последний год.
Задача 2.8. Определите сумму на сберегательном счете в Сбербанке РФ по состоянию на 8ч. 50мин. 1 апреля 2006 г., если вклад сделан 1 января 2006 г. в размере 400 тыс. руб., а процентная ставка равнялась 10% годовых, но с 31 января введена новая ставка - 9%. Ответ дать с точностью до рублей, округляя по обычным правилам.
1.4.4. Начисление процентов несколько раз в год. Посмотрим, как будет выглядеть формула (4.3), если проценты будут начисляться не один, а несколько раз в год. Пусть в году будет m периодов начисления процента, тогда рост (индекс) за один период будет равен: (1.4.8) FV = PV(1+r/m) (1.4.9) но количество периодов начисления увеличится и составит n×m, а итоговая формула примет вид: FV = PV(1+r/m)nm Если рассматривать это с точки зрения индексного подхода, то формула не изменилась: рост за период возводится в степень равную количеству периодов. Но дело в том, что по договоренности в качестве относительного прироста r всегда выступает прирост за год, поэтому, если период начисления отличается от годового, то относительный прирост надо скорректировать разделив годовую ставку на количество периодов начисления в году. Задача 2.9. Известный бизнесмен и экономист Генри Форд, нанимая специалистов, говорил: «Обычно я увеличиваю зарплату своих специалистов на 4% в год. Это может быть либо увеличение на 4% в конце года, либо увеличение на 2% в конце первого и второго полугодия, либо на 1% в конце каждого квартала. Какой вариант выберете Вы?» После ответа Форд либо брал, либо отказывал претенденту в работе. В случае какого ответа Форд брал человека на работу? 1. Увеличить на 4% в год; 2. Увеличить на 2% каждое полугодие; +3. Увеличить на 1% ежеквартально; 4. Не имеет значения: все варианты равноценны; 5. Я готов у Вас работать и без увеличения зарплаты.
2.2.1. Момент выплаты процента. Процентные платежи могут начисляться в конце каждого периода, и такие проценты называют декурсивными (postnumerando), а могут начисляться в начале каждого периода. Такие проценты называют - антисипативными (prenumerando) процентами. Все рассмотренные выше проценты - декурсивные или постнумерандо. В данном разделе мы рассмотрим проценты начисляемые в начале периода. В некоторых неадекватных учебниках (особенно выложенных в Интернете) можно прочитать, что: "Антисипативным методом начисления процентов обычно пользуются в чисто технических целях". На самом деле, антисипативные проценты имеют огромный финансовый смысл: 1. Таким способом начисляются проценты по вексельным кредитам; 2. Таким способом начисляются проценты по ломбардным кредитам; 3. Таким способом начисляются проценты в периоды гиперинфляции. Вексель. Вид ценной бумаги, представляет собой денежное обязательство строго установленной законом формы. Является безусловным и бесспорным долговым документом. Ломбардный кредит. Кредит, который выдается под залог какой либо ценности. Ценность возвращается владельцу после полного погашения кредита. Почему при вексельном и ломбардном кредите проценты начисляются пренумерандо? Максимальная сумма, которую кредитор получит от заемщика - сумма указанная в векселе. Для ломбарда максимальная сумма равна ценности залога. Поскольку при погашении кредита общая сумма выплат с процентами не может превышать указанных сумм, то начисленные на сумму залога проценты должны быть учтены заранее. Для вывода формулы роста (индекса роста) кредитов с антисипативным методом начисления процентов используем формулу (1.1.1). 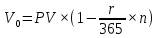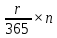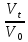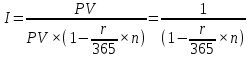В соответствии с этой формулой имеем: Ценность актива на начало периода  , где r - годовая процентная ставка начисляемых методом простых процентов; n - количество дней до погашения выданного кредита;  - проценты начисленные пренумерандо и учтенные кредитором;Ценность актива на конец периода Vt = PV поскольку, в соответствии с формулой (1.1.1) I=  , то окончательно имеем: (2.2.0)  Задача 2.10. Банкир дает ломбардный полугодовой кредит из расчета 30% годовых с возвратом суммы кредита в конце срока кредита. Рассчитать годовой индекс роста данной операции. Ответ округлить до четырех знаков после запятой по обычным правилам арифметики.
В период гиперинфляции проценты начисляются методом пренумерандо из тех соображений, что за время пользования кредитом они могут быть пущены в оборот и дать дополнительный доход. Задача 2.11. В 1992 году инфляция составляла 180% в год. Банк выдает кредит на 90 дней под 210% годовых. Рассчитайте реальный интерес банка при начислении процентов постнумерандо и пренумерандо, если при начислении пренумерандо проценты банк дает в залог другому банку под 186% годовых. (Используйте технику обыкновенного банковского учета векселей по правилу (360, 360))
2.2.2. Сравнение процентов с разными методами начисления.  Чтобы сравнить доходности двух активов достаточно сравнить их индексы роста (темпы роста) Задача 2.12. Какой процент годовых по депозитам сроком на 45 дней эквивалентен учетной ставке дисконтного векселя, выданного на тот же срок под 18% годовых?Решить, используя формулу (360, 360) и ответ дать с точностью до десятых процента, округляя по обычным правилам.
Задача 2.13. В состав услуг КМБ-банка в 2003 году входила продажа своих дисконтных векселей под 18% годовых по обычным правилам учета дисконтных векселей с базой 360 дней. Что выгоднее банку как заемщику и насколько: взять кредит 200 тыс. руб. под 19% годовых сроком на 60 дней с возвратом суммы кредита (принципала) и суммы процента в конце срока кредита или получить те же деньги путем продажи векселей на тот же срок? Дайте ответ в виде денежной разницы между вариантами.
2.2.4. Нахождение процентной ставки и других параметров актива. Иногда важно найти процентную ставку исходя из тех данных, которые имеются в распоряжении финансового менеджера. Также важно понимать и уметь рассчитывать стоимость тех ценных бумаг, которые имеются в распоряжении финансового менеджера. Задача 2.14 (Шапиро Л.Б.) Вексель на сумму 9000 рублей учитывается по простой учетной ставке за 120 дней до погашения с дисконтом равным 600 рублей в пользу банка. Определить величину этой годовой учетной ставки.
Задача 2.15 (Шапиро Л.Б.) В банк 6 мая предъявлен для учета вексель на сумму 14 000 рублей со сроком погашения 10 июля того же года. Банк учитывает вексель по простой учетной ставке 40% годовых. Определить сумму, которую получит векселедержатель от банка. За какое время до срока платежа операция имеет смысл? (Используйте технику обыкновенного банковского учета векселей по правилу (360, 360))
2.2.5. Эквивалентные процентные ставки.  Две процентные ставки называются эквивалентными, если применение их к одинаковым суммам и в течении одинакового времени приводит к одинаковым результатам. Общий принцип расчета эквивалентных процентных ставок состоит в том, что если ставки эквивалентные, то они обеспечивают одинаковый рост (темпы роста). Поэтому, для нахождения эквивалентных ставок мы записываем уравнение равенства темпов роста и из этого уравнения находим искомое. Задача 2.16 (Шапиро Л.Б.) Кредит предоставляется под 5% сложных годовых сроком на 8 лет. Клиент хочет получить его под простые проценты. Какая ставка простых процентов может быть предусмотрена контрактом?
Задача 2.17. Кредит предоставляется под 5% сложных годовых сроком на 8 лет. Клиент хочет получить его под простые проценты. Какая ставка простых процентов может быть предусмотрена контрактом, если простые проценты начисляются пренумерандо?
Задача 2.18. Банкир дает ломбардный полугодовой кредит из расчета 30% годовых. Определить эквивалентную ставку процента при выдаче кредита под простые проценты. Ответ дать до сотых долей процента, округляя по обычным правилам арифметики.
2.2.6 Эффективная процентная ставка.  Эффективной процентной ставкой rэф соответствующей данной процентной ставке, называется ставка сложного процента, эквивалентная данной процентной ставке и не зависящая от периодов начисления. Пояснение: эффективная процентная ставка, это годовая доходность процентов начисляемых различными способами. Задача 2.19 (Шапиро Л.Б.) Банк выплачивает по вкладам 10% годовых. Какова реальная доходность вкладов при начислении процентов: а) по полугодиям, б) ежеквартально, в), ежемесячно.
Задача 2.20. Инвестор вложил свои сбережения в Управляющую Компанию. Сумма вложений - 600 т.руб. В первый год портфель с минимальным риском принес 5,6% годовых и инвестор попросил повысить риск вложений. Второй году принес уже 12,4% годовых, третий год принес прибыль равную 36 т.руб, а четвертый - 38,8 тыс.руб. Найти эффективную ставку вложений.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
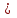(1+(31+30+31+30+31+31+16)*0,16/365)= Х
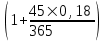X = 8958,5
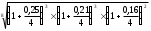- 1 = 0,0530887. откуда в год 0,0530
4 =0,2124
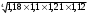- 1)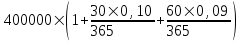
= 409 205 руб
= 
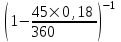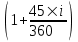. Ответ: i = 0,184 или 18,4%.
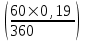= 6333,33 руб.
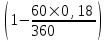× 200000.
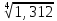= 1,070 годовых тогда r = 1,07-1 = 0,07 или 7,0%