Методичка к экзаменам_магистратура. Методические материалы по написанию вступительного теста в магистратуру вшфм. Раздел Финансовая математика. Индексы, доходности
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Раздел 3. Финансовая математика. Временная стоимость денег Рубль вчера, сегодня и завтра - разные денежные единицы. Если актив приносит денежные потоки разнесенные по времени, то рассчитать его стоимость, доходность и рост можно только сравнив эти потоки, но сравнивать несравнимые величины можно только одним способом: сделать их сравнимыми, т.е. привести к одному времени.  Следствием временной стоимости денег является тот факт, что если мы хотим сравнивать суммы вложенные или изъятые в разное время, то они должны быть приведены к одному и тому же моменту. При этом: 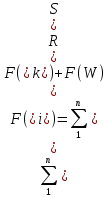 где:F(Si) - приведенные вклады F(Rt) - приведенные выплаты F(W) - остаток на счете в момент n  (3.1.0) Приведением денежных потоков к одному времени называется процесс, при котором все потоки "прошлого" наращиваются к моменту приведения, а все потоки "будущего" - дисконтируются по той же ставке. Для лучшего запоминания можно использовать следующее мнемоническое правило:  В принципе, можно привести суммы к любому моменту времени, но при этом следует соблюдать правило: Все суммы стоящие слева от момента, к которому приводятся, наращиваются, а все суммы стоящие справа - дисконтируются  (3.1.1) Таким образом, этапы приведения состоят в следующем: 1. Построение "временной шкалы". Одно деление этой шкалы, т.е. одна "единица времени" - период начисления. Это может быть начисление процентов на сумму вклада, периодические выплаты купонов и т.д. Сверху шкалы записываются инвестиции в актив, внизу - деинвестиции в тот же актив. 2. Выбор момента к которому будут приведены суммы. Поскольку выбор момента приведения не влияет на результат, то он может быть любым, но для удобства выбирают: а) начальный момент - если знают потоки от актива в будущем и хотят рассчитать его текущую ценность; б) момент окончания пользования активом - если хотят узнать его конечную ценность; в) любой другой момент - как правило, это момент принятия решений для увеличения или уменьшения инвестиций в актив для приведения его ценности к требуемому объему. 3. Расчет индекса роста для одного периода начислений. Если период не совпадает с годовым, то доходность выраженная в годовых делиться на количество периодов начислений. 4. Каждая сумма инвестиций входит в уравнение (3.1.0) со знаком "+" и умножается на индекс роста одного периода в степени равном количеству периодов между моментом инвестиций и моментом приведения. Знак степени зависит от правила (3.1.1). Суммы деинвестиций входят в уравнение со знаком "-" по тому же правилу - умножаются на индекс роста в соответствующей степени.  ? Задача 3.1 (Шапиро Л.Б.) Клиент положил 2 года назад 600 руб. в банк. Банк выплачивает проценты по ставке r = 5% годовых ежемесячно. 8 месяцев тому назад клиент снял со счета 400 руб., а сегодня снял еще 100 руб.. Через 3 месяца он желает вложить некоторую сумму так, чтобы через год от сегодняшнего момента закрыть счет, получив при этом 500 руб. Какую сумму он должен вложить? К 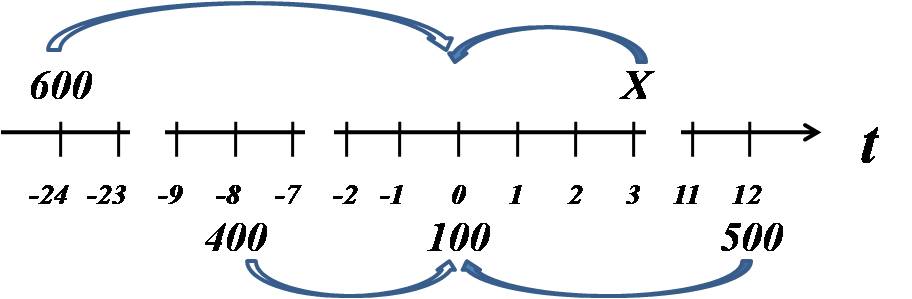 ак и для предыдущей задачи отобразим условия на временной шкале: ак и для предыдущей задачи отобразим условия на временной шкале:
Если за момент расчета взять вложение неизвестной суммы, то имеем: 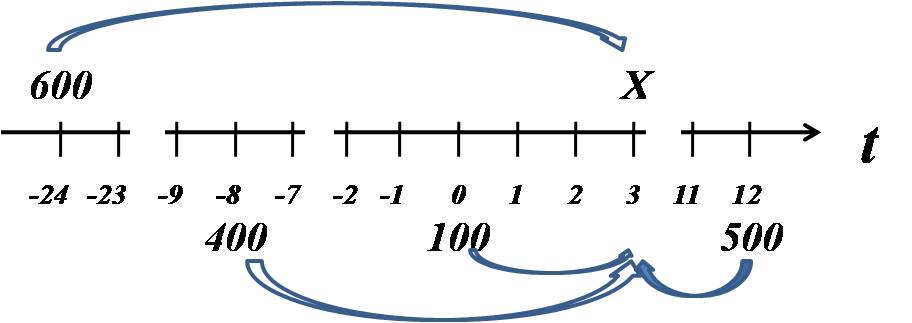 В таком случае наше уравнение будет выглядеть несколько иначе:
Раздел 4. Финансовая математика. Финансовые ренты, аннуитет, перпетуитет. 4.1.4. Финансовые ренты. Современная ценность финансовой ренты.  Современная ценность А финансовой ренты равна текущей ценности ее наращенной суммы. Другими словами, для того, чтобы найти современную ценность ренты надо продинсконтировать наращенную сумму к современному моменту. Рассчитаем коэффициент приведения ренты для которой проценты начисляются один раз в год, платежи делаются один раз в год. Используя (7.0) и (4.13) имеем: Индекс роста финансовой ренты: 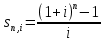 Индекс дисконтирования: Iдисконт = (1+i)-n  (4.1.10) Тогда, дисконтируя, имеем: an,i = 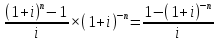 Таблица значений современной ценности рент:
Задача 4.1 (Шапиро Л.Б.) Какую сумму необходимо положить в банк, чтобы в течении следующих 10 лет ежегодно получать 30 000 руб., исчерпав счет полностью, если снимать деньги каждые два месяца равномерными частями? Банк начисляет 5% годовых раз в год.
Задача 4.2 (Шапиро Л.Б.) Какую сумму необходимо положить в банк, чтобы в течении следующих 10 лет ежегодно получать 30 000 руб., исчерпав счет полностью, если снимать деньги каждые два месяца равномерными частями? Банк начисляет 5% годовых раз в квартал.
4.1.5. Финансовые ренты. Современная ценность бессрочной финансовой ренты.  Современной ценностью вечной ренты А называется сумма, которую нужно вложить в начальный момент (в банк), чтобы неограниченно долго ежегодно снимать сумму R 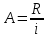  (4.1.19) Формула (4.1.19) получается предельным переходом n→∞ в формуле (4.1.10), тогда (1+i)-n → 0 Задача 4.3 Государство заняло сумму у банка на условиях "вечной ренты", то есть согласилось выплачивать ежегодно в конце года по 1 млн. руб. не возвращая долга. Какова минимальная сумма кредита (в миллионах рублей), если, заключая договор, стороны исходили из 10% годовых за такой кредит?
Раздел 5. Экономическая теория. Норма прибыли, реальный доход и пр. В экономике и финансах очень часто необходимо рассчитать не просто рост какого либо текущего показателя, а рост этого показателя по отношению к так называемому базовому показателю. Это необходимо для возможности сопоставления изменения текущего показателя при изменяющейся базе расчетов. Без такого сопоставления невозможно было бы анализировать изменения текущих показателей либо за различные промежутки времени, либо в различных местах, либо по отношению к глобальному фактору. Математически, нормирование выглядит так:  (1.5.0) 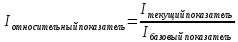 При этом базовыми показателями могут быть уровень инфляции, рост экономики страны в целом, рост рынка или сегмента рынка, отраслевой (или странновой) рост в различных странах и т.д. 1.5.1 Номинальная и реальная доходность.  Номинальными называются показатели, рассчитанные в текущих ценах, а реальными - в сопоставимых ценах, часто называемых базовыми или ценами базового периода. Используя соотношение (1.5.0) и считая базовыми показателями покупательную способность рубля имеем. тогда  (1.5.1)  (1.5.2) Задача 5.1. Для защиты населения США от инфляции Правительство выпускает облигации TrIPS с «плавающим» купоном (купон индексируется по темпам инфляции). Если среднегодовая инфляция в течении 5 лет составила 2,2 % годовых, то что выгоднее обывателю: размещение денег на депозите в банке под 4 % годовых сроком на 5 лет или покупка 5-ти летний TrIPS с доходностью 1,8 % годовых
Задача 5.2. Сколько процентов реальной зарплаты "съедает" месячная инфляция равная 50% при тридцатидневной задержке выплаты зарплаты?
Задача 5.3 Какую сумму надо внести в банк под 20% годовых при начислении сложного процента с годовой капитализацией процента, чтобы через 4 года накопить сумму эквивалентную сегодняшним 100 тыс. руб., если индекс цен за 4 года составит 2? Округлите ответ до рублей по правилам математики. Варианты ответа: 1) 96568руб. 2) 97845руб. +3) 96451руб. 4) 89238руб. 5) Нет верного ответа.
1.5.2 Сравнение доходностей в разных валютах.  Доходность, рассчитанная в долларах, но номинированная в рублях, связана с доходностью рублевых активов известным соотношением: 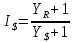 где Y$YR - ожидаемая доходность по долларовым и рублевым вкладам.  (1.5.3) В данном случае базовым показателем является индекс роста долларовой доходности, а текущим - рублевой. Задача 5.4 Насколько изменится покупательная способность доллара в России, если за год курс вырастет с 31 руб. до 32 руб. за доллар, а инфляция составит около 15%? Ответ дайте с точностью до десятых процента, округляя в большую сторону. Варианты ответа: 1) -20,5%. 2) -15,3%. +3) -10,2%. 4) -12,8%. 5) Нет верного ответа.
1.5.3 Нормирование показателей при планировании и бюджетировании.  При анализе гибких бюджетов, отклонения q по каждой i-ой статье, необходимо корректировать на изменение индекса плана: 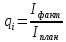  (1.5.4) В данном случае базовым показателем является индекс роста долларовой доходности, а текущим - рублевой. Задача 5.5. Компания, торгующая в России классической телефонией, спланировала объем продаж в конце 2007 года в размере 6,5 млн. рублей. Фирма торгует аппаратурой за рубли, но закупает его за валюту. В середине года стало понятно, что курс доллара, рассчитанного Миэкономразвития будет примерно на 15% больше, кроме того, прогноз по росту инфляции говорит о том. что она вырастет примерно на 10% в годовом исчислении. Проведите коррекцию плана продаж.
Задача 5.6. Авиакомпания - лоукостер планирует выйти на новый рынок авиаперевозок и занимается калькуляцией удельных переменных затрат. В основе взята калькуляция удельных затрат местной авиалинии, которая подвергается тщательной ревизии. Удельные (в пересчете на 1-го пассажира) расходы на топливо и з/п летного персонала составляют $24 при 67% загрузке самолета. Какими будут эти затраты при 100% загрузке самолета? Ответ округлите до центов.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

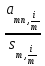
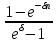
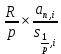
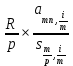
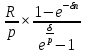
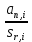
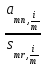
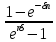
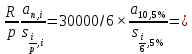 236 432 .руб.
236 432 .руб.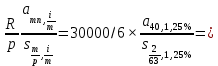 235 439 .руб.
235 439 .руб.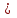 0,1 = 1 млн. руб. Ответ: 10 млн. руб.
0,1 = 1 млн. руб. Ответ: 10 млн. руб.