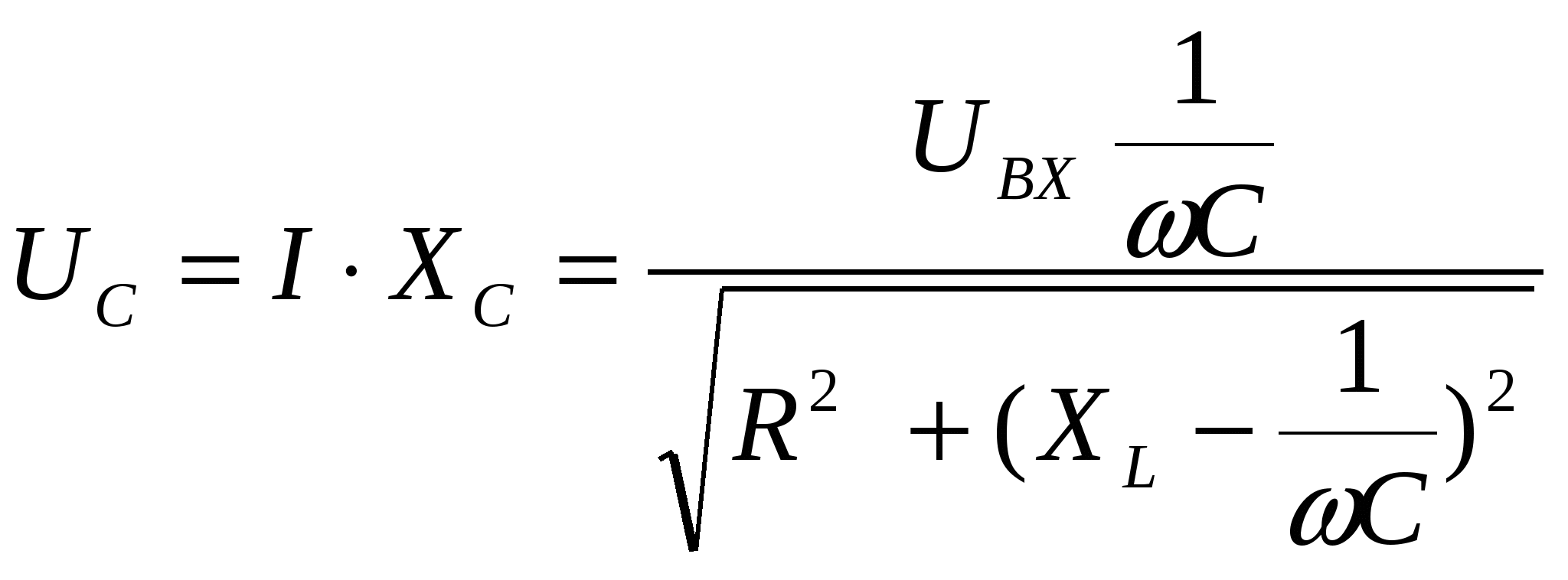Методические рекомендации по срс при подготовке к выполнению лабораторных работ по курсу Электротехника и Электроника
 Скачать 1.19 Mb.
|
|
Электротехника и Электроника Методические рекомендации по СРС при подготовке к выполнению лабораторных работ Часть 1: Электрические цепи, трансформаторы, электрические машины Казань 2008 УДК ………………. Составители : к.ф.м.н., доц. А.Ш.Мухтаров ст.препод. А.В. Толмачева асс.Сабитов Р. …. Электротехника и Электроника: Методические рекомендации по СРС при подготовке к выполнению лабораторных работ по курсу «Электротехника и Электроника» ч.1:Электрические цепи, трансформаторы, электрические машины. / Каз.гос.технол. ун-т; Сост.: А.Ш.Мухтаров, А.В. Толмачева, Т.В. Варнакова, Р.Ф. Сабитов, Казань, 2008. …..55с. Содержатся методические указания к выбору оптимального режима работы с литературой и учебными пособиями при подготовке к выполнению и сдачи лабораторных работ. Работа предназначена для студентов не электротехнических специальностей ( технологов) всех форм обучения. Печатается по решению методической комиссии по циклу естественнонаучных дисциплин под ред. к.т.н., доц. В.Г.Макарова Рецензенты: д.т.н., проф…………………….. Кафедра ЭО КГТУ ( зав.каф. д.т.н.проф. А.Ю.Афанасьев) Лицензия 020404 от 06.03.1997г. Подписано в печать……… Формат 68х68/16. Бумага писчая Печать RISO…..усл.печ.Л ….……уч.-изд.Л. Тираж…. Экз. Заказ ……. 420075, Казань, К.Маркса 68
Тема 2. ИССЛЕДОВАНИЕ НЕРАЗВЕТЛЕННОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА. РЕЗОНАНС НАПРЯЖЕНИЙ Цель работы: 1) изучить процессы в цепи переменного тока, состоящей из последовательно соединенных катушки и конденсатора; 2) изучить явление резонанса напряжений и условия, при которых оно наблюдается; 3) освоить методику построения векторных диаграмм для цепи с последовательным соединением элементов. Приборы и оборудование Работа выполняется на универсальном стенде, где установлен лабораторный автотрансформатор (ЛАТР) и необходимые приборы. Индуктивная катушка и батарея конденсаторов с регулируемой (с помощью выключателей) емкостью находятся на столе. Электрическая цепь собирается с помощью комплекта проводов в соответствии со схемой соединений (рис.1). Контрольные вопросы Вопрос 1. Нарисовать схему замещения электрической цепи. Объяснить какие процессы отражают элементы этой схемы. Ответ 1: Каждое ЭТ устройство заменяют его условным (согласно ГОСТ) изображением. Такие схемы называются принципиальными. Принципиальная схема лабораторной установки представлена на рис.1. 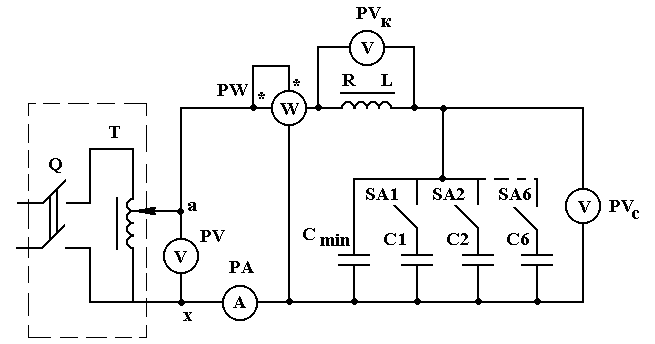 Рис.1 Для количественного расчета цепи необходимо иметь схему замещения. В схеме замещения ЭТ устройство заменяют ее идеальным образом, передающим его основные свойства (электрические и энергетические характеристики). Так как индуктивная катушка обладает активным и индуктивным сопротивлениями, то на схеме замещения этой цепи (рис.2), катушка представлена в виде 2-х последовательно соединенных элементов -резистора R и индуктивности L , а батарея конденсаторов - емкостным элементом С. Измерительные приборы (амперметр, вольтметры, ваттметр) в схеме замещения не представлены, т.к. они потребляют незначительную по сравнению с вышеуказанными элементами мощность и незначительно влияют на электрические характеристики цепи.
Сопротивление катушки R обусловлено сопротивлением провода катушки индуктивности. При прохождении через него тока I оно нагревается и на нем выделяется мощность:  . При прохождении через катушку индуктивности L тока I вокруг нее образуется магнитное поле. Катушка накапливает магнитную (реактивную) энергию. Соответствующая мощность равна:  , где  .При прохождении тока через емкостной элемент С в нем образуется электрическое поле. Емкость накапливает электрическую (реактивную) энергию. Соответствующая мощность равна:  , где  .Вопрос 2. Записать выражение для полного сопротивления, тока и коэффициента мощности при резонансе напряжений. Ответ 2.1: Из схемы замещения следует, что электрическая цепь состоит из 3-х последовательно соединенных сопротивлений:  . Полное сопротивление следовало бы считать равным сумме сопротивлений. Однако т.к. в цепях переменного тока реактивные элементы влияют на сдвиг фаз между током и напряжением на этом элементе, сопротивления  заменяют их комплексными образами  и полное сопротивление  рассчитывают как сумму комплексных сопротивлений: ;Величина (модуль) полного сопротивления равна:  ;При резонансе напряжений  . Поэтому  . Реактивные сопротивления друг друга компенсируют, полное сопротивление  становится чисто активным и равным сопротивлению катушки  . Ответ 2.2. Из анализа схемы замещения (из 2-го закона Кирхгофа) следует, что:  При резонансе напряжений С и  , поэтому ток равен : .Вывод: При резонансе ток в цепи  и определяется только отношением входного напряжения к чисто активному сопротивлению катушки.Ответ 2.3В цепи переменного тока различают активную  , реактивную  и полную  мощность, которые рассчитываются следующим образом: , Вт; , ВАр; , ВА.Реактивная составляющая полной мощности цепи находится как разность индуктивной QL и емкостной QC ее составляющих:  Коэффициент мощности электрической цепи cosφ показывает долю активной мощности Р в полной мощности цепи S:  .Полная мощность рассчитывается по формуле:  .Вариант ответа a) При резонансе напряжений: cosφ0=Р0/UI0. Но Р0 =I02R , U=I0·R. После подстановки в выражение для cosφ0 имеем: 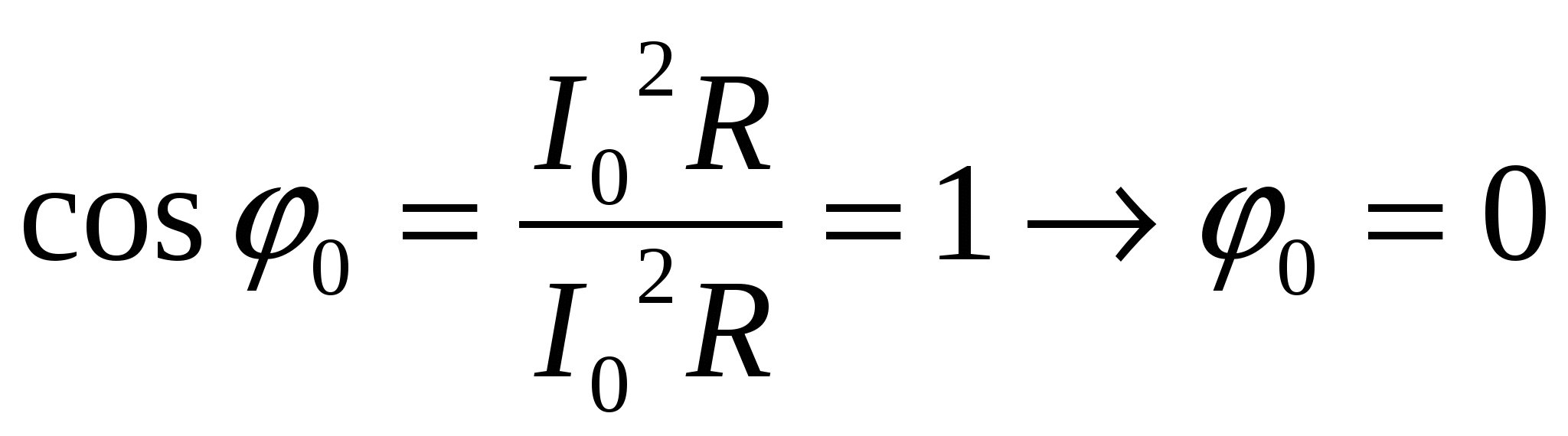 .Вариант b) При резонансе суммарная реактивная мощность равна нулю  , поэтому полная мощность S равна чисто активной мощности P. Следовательно: .Вывод: При резонансе напряжений +коэффициент мощности  , т.е. вся подводимая мощность расходуется только на нагрев проводов катушки индуктивности.**)  можно определить из соотношения  Вопрос 3. В чем заключается явление резонанса напряжений и при каких условиях оно возникает? Ответ 3.1: В данной цепи при равенстве индуктивного  и емкостного  сопротивлений полное сопротивление цепи будет минимальным и чисто активным Z=R, а ток – максимальным  . Падения напряжения на индуктивном и емкостном элементах рассчитываются по закону Ома:  ,  и т.к. величина напряжения на идеальной индуктивности UL равна напряжению на емкости UC.  , но фазы напряжений UL и UC противоположны (сдвинуты на 180°).Режим работы цепи c последовательным соединением R,L,C элементов при котором и  (или  ) называют резонансом напряжений. Сумма комплексов напряжений ŪL и ŪC равна нулю, следовательно и модуль суммы будет равен нулю. Вольтметр, измеряющий падение напряжения (модуль комплекса напряжения) на участке цепи с идеальной индуктивностью и емкостью, покажет значение =0. При этом ток  и напряжение  ВХ совпадает по фазе (коэффициент мощности  , φ0 =0). Активная мощность  имеет наибольшее значение, равное полной мощности S, в то время как реактивная мощность цепи оказывается равной нулю:  .При резонансе напряжения на емкости и на индуктивности могут значительно превышать подводимое напряжение U, если  и  значительно превышают R: ,  .Физическая причина возникновения повышенных напряжений – это колебания значительной энергии, запасаемой попеременно в электрическом поле емкостного и магнитном поле индуктивного элементов. При резонансе напряжений малые количества энергии, поступающей от источника и компенсирующие потери энергии в активном элементе – сопротивлении R, достаточны для поддержания незатухающих колебаний в системе относительно больших количеств энергии электрического и магнитного полей. Причем в любой момент времени суммарная энергия электрического и магнитного полей остается постоянной. Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции. **) Для мощных двигателей отношение сопротивлений обмоток XL/R на промышленной частоте составляет несколько десятков. Напряжение питания двигателей обычно <380В. Поэтому в случае резонанса, напряжение на обмотке ULпревысит напряжение питания в деcятки раз (UL>>3800В). В тоже время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике в различных приборах и устройствах, основанных на резонансных явлениях. Вопрос 4. Изменением каких параметров электрической цепи (см. рис.1) можно получить резонанс напряжений ? Ответ 4: При резонансе напряжений выравниваются реактивные сопротивления ХL=XC. Т.к. ХL=ω·L , а XC=1/ωС , то равенства сопротивлений можно добиться тремя способами:
Вопрос 5. С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений в электрической цепи? Ответ 5: 1) В данной лабораторной установке опыты проводятся при постоянных величинах ω и L. По мере увеличения емкости от минимального до резонансного значения С0=1/ωXL, полное сопротивление цепи 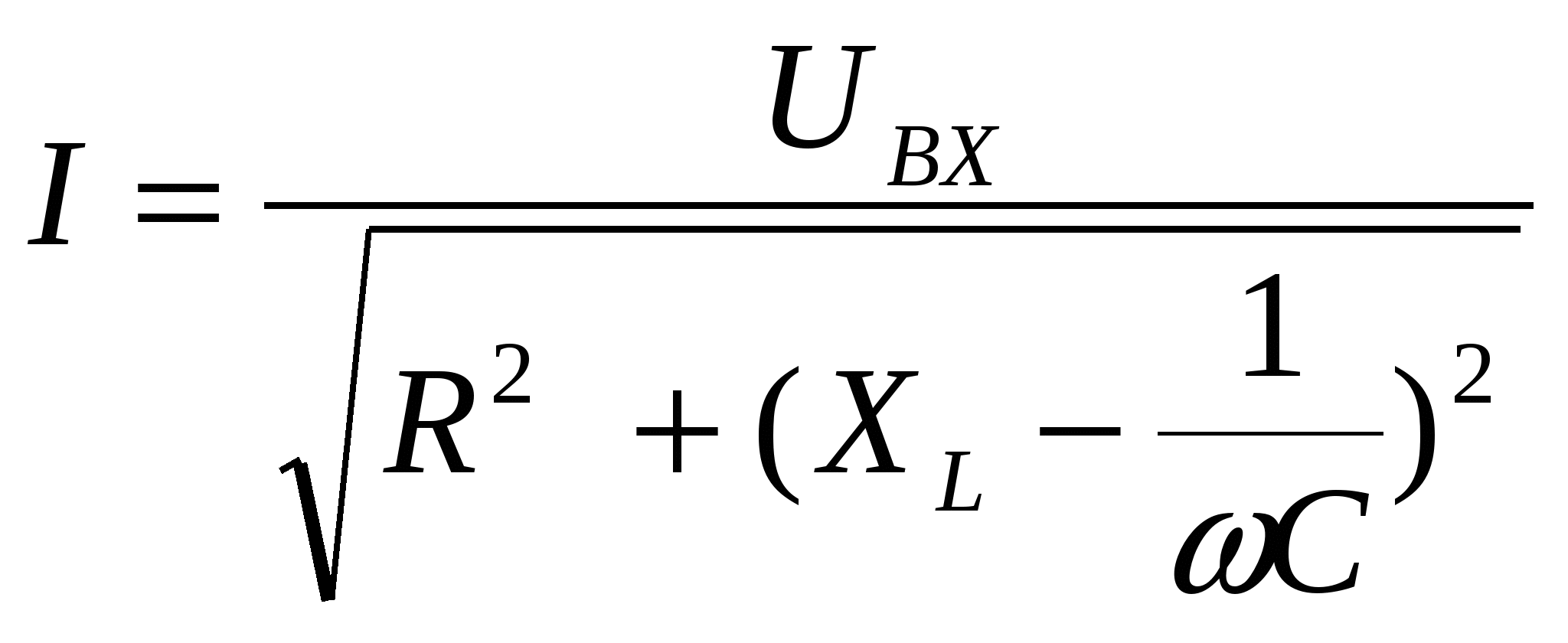 будет уменьшаться, при этом ток в цепи согласно формуле для тока  будет расти. При резонансе он достигнет максимального значения .Вывод 1 1: Амперметр покажет максимальное значение тока. 2) Т.к. UL=I·XL, то падение напряжения на индуктивности UL будет расти пропорционально росту тока. При резонансе напряжений, это напряжение будет максимальным. Однако вольтметр PVК измеряет, согласно схеме замещения, падение напряжения на участке цепи из 2-х последовательно соединенных элементов: сопротивлений катушки R и индуктивности ХL. Падение напряжения на сопротивлении R равно UR= I·R=Uвх, следовательно при резонансе это напряжение также будет максимальным. Вывод 2: 1)Вольтметр PVК также покажет максимальное значение  2)Падение напряжения на емкости С, измеряемое вольтметром PVC, равно: 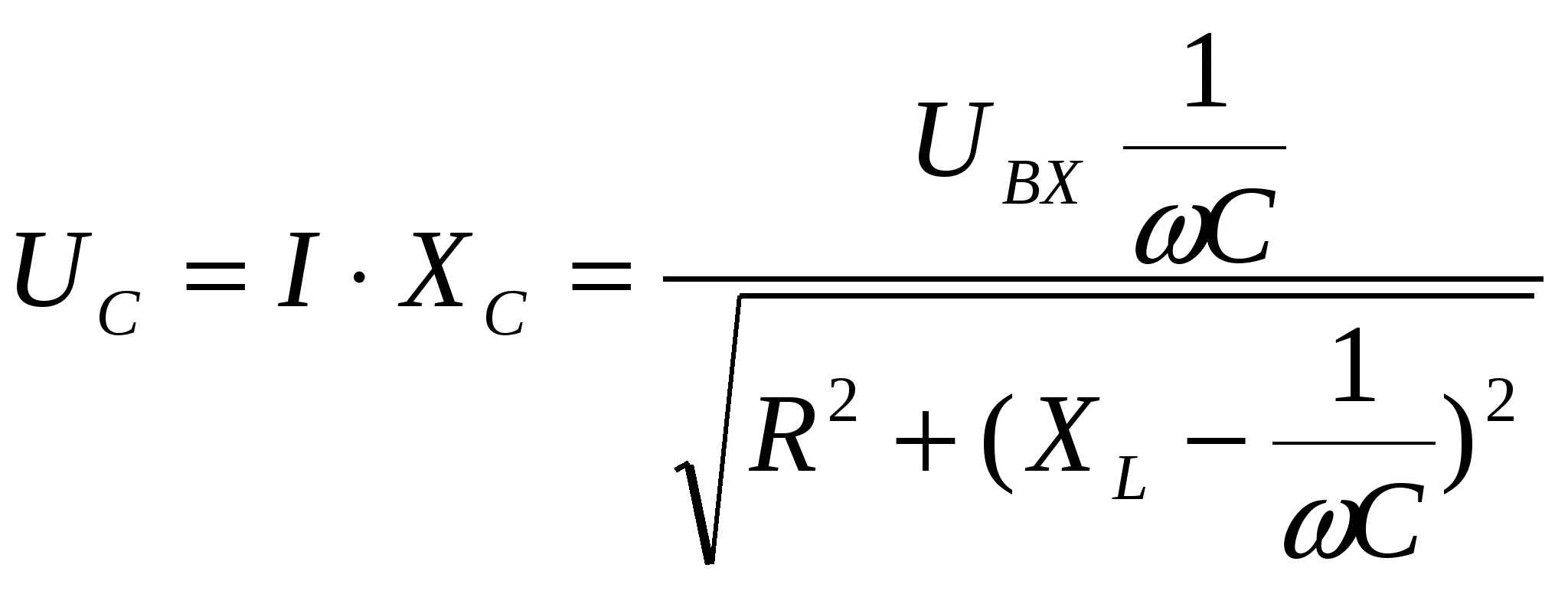 . Т.к . ток в цепи один , а величины сопротивлений ХL, XC при резонансе одинаковы, то и напряжения одинаковы UL =UС. При этом Uвх = UR. При резонансе =  . Следовательно показания вольтметров PVК и PVC будут разными. Очевидно, что UК > UC.Вывод 3: при резонансе показания вольтметра PVК больше показания вольтметра PVC . 4) Ваттметр PW измеряет активную мощность потребляемую цепью. Т.к. при резонансе ток максимальный, а активная мощность Р = I2·R, то и мощность P будет максимальной. Вывод 4: Ваттметр покажет максимальное значение Рмакс = I02·R= U2вх / R. Вопрос 6: Провести анализ построенных векторных диаграмм до и после резонанса напряжений и объяснить, в каком случае входное напряжение опережает ток, а в каком – отстает от тока. Ответ 6.1: Напряжение питающей сети, подведенное к цепи, равно векторной сумме напряжений, действующих на отдельных участках этой цепи и может быть записано по второму закону Кирхгофа в комплексной форме:  , или в виде  Векторная диаграмма строится на комплексной плоскости на основании этого уравнения. Ток I и напряжение UR = I ·R откладываем вдоль реальной оси. Напряжение ŪL = +j·I ·XL откладываем на положительной мнимой оси. Напряжение ŪС = - j·I ·XС откладываем на отрицательной мнимой оси Если сопротивление XL > XС, то UL>UC ( рис 6.а). Если сопротивление XL < XС, то UL 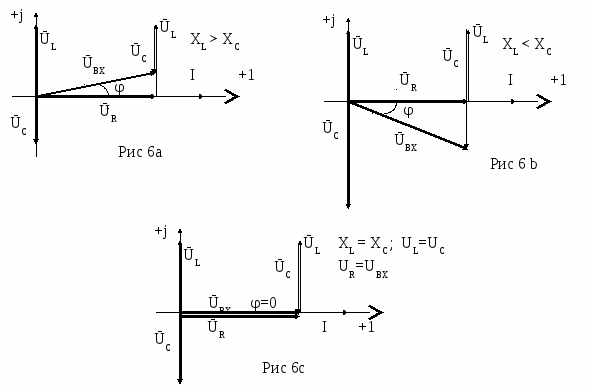 Вывод: Из векторной диаграммы ( рис 6а) видно: что если XL > XС, то входное напряжение Uвх опережает ток I. Если сопротивление XL < XС ( рис 6 b) , то ток I опережает Uвх. Вопрос7. По схеме замещения исследуемой цепи проанализируйте, к чему приведет изменение активного сопротивления электрической цепи при резонансе напряжений. Ответ 7. При резонансе напряжений I0=Uвх/R. Поэтому при увеличении(уменьшении) сопротивления Rк ток (показания амперметра РА) и активная мощность(показания ваттметра РW) будет уменьшаться (увеличиваться). Показания вольтметров РVК и РVС будут вести себя аналогичным образом: UC=I0·XC= Uвх/R·XC , UL=I0·XL= Uвх/R·XL. Вопрос8. Сохраняется ли резонанс напряжений, если изменить только напряжение питающей сети? Ответ 8. При резонансе напряжений XC =XL. Сопротивления XC и XL не зависят от напряжения питающей сети. Вывод: резонанс напряжений сохранится. ***) На самом деле индуктивность катушки с железным сердечником может зависеть от протекающего через катушку тока, если сердечник не насыщен или сердечник изготовлен из не магнитно-мягкого материала. В магнитно-мягком материале магнитная проницаемость не зависит от тока катушки. Вопрос9. Объяснить ход кривых полученных в этой работе. Ответ 9. Необходимо объяснить зависимости Z, Р, I, Uc, UL, cosφ = f (C). 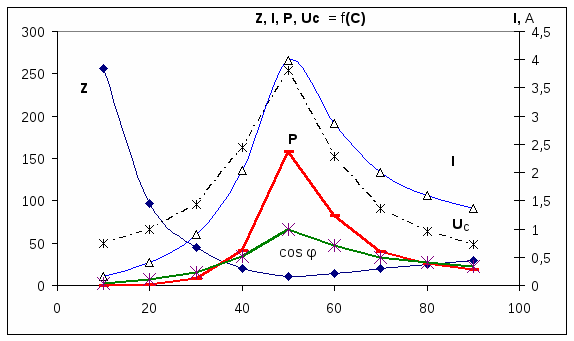 9.1 Сопротивление Z зависит от С согласно формуле:  В данной лабораторной работе XL и R неизменны, при этом начальное значение Xc >>XL >>R , поэтому Z определяется в основном величиной Xc. Из анализа формулы следует , что при увеличении емкости С, сопротивление Xc=1/ωС уменьшается и Z также уменьшается. При резонансе Z минимально и (С = С рез (50мкф)) XC=XL= 63Ом , R =14 Ом). При дальнейшем увеличении емкости Xc становится меньше XL и Z незначительно возрастает. 9.2 Ток I зависит от С согласно формуле: I=U/Z. Т.к. U=const, поэтому зависимость тока I от емкости С обратная зависимости Z от С. С увеличением емкости С, ток I будет возрастать, при резонансе пройдет через максимум ( I0= U/R=40/14=2,85A),а затем будет уменьшаться. 9.2 Мощность Р=I2R . Поэтому Р пропорциональна зависимости квадрата тока I2 от С. График зависимости Р от С –график зависимости квадрата тока от емкости С. С увеличением тока, мощность Р возрастает, проходит через максимум (Рмакс= U2/ R=402/14=114,5Вт) , затем уменьшается. 9.3 Напряжение UL = I·XL. Т.к. XL=const, то график зависимости UL от С подобен графику зависимости I от С. Он отличается только масштабом (множителем XL).
В начале опыта сопротивление ХС значительно больше ХL и R, а ток в цепи мал ( в пределе при С=0 →ХС= ∞→ I=0 ), поэтому падение напряжения на катушке UК мало и напряжение UC близко к напряжению на входе UВХ (UВХ =40В). При резонансе напряжение UC максимальное и равно UC =I0 ·XC =40 /14 ·63=180B. При дальнейшем увеличении емкости сопротивление XC уменьшается, в пределе при С= ∞, XC=0, а ток в цепи будет конечным и равен: 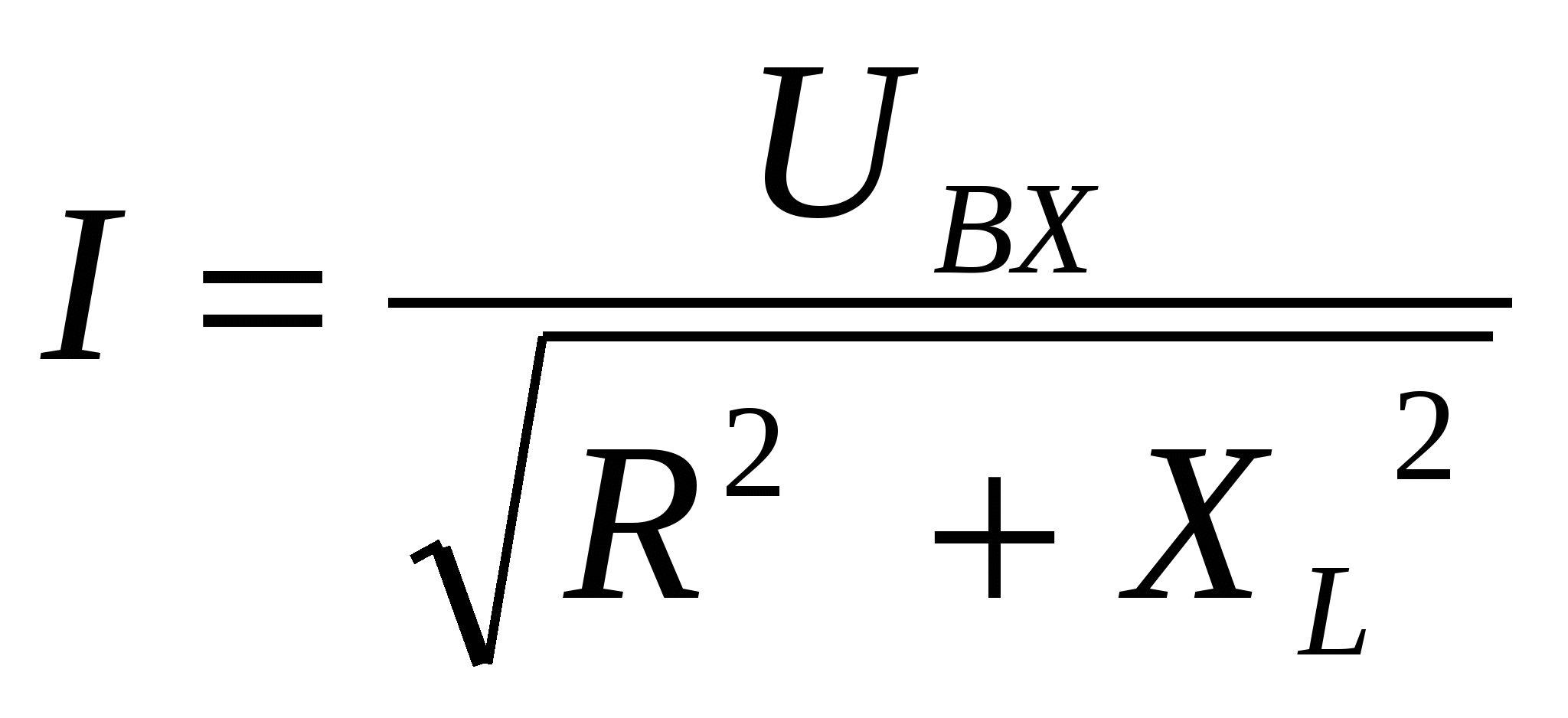 , соответственно падение напряжения: UC=I·XC →0.
 . Умножим и поделим cosφ на U. → сosφ = U/Z · R/U= I·R/U= b · I, где b= R/U=const.Поэтому график зависимости cosφ от С будет подобен графику зависимости I от С. С увеличением емкости С, cosφ будет возрастать, при резонансе (XL=XC → Z=R ) он будет максимальным (cosφ0 = R/R =1) и затем будет уменьшаться. Вопрос10. Какую опасность для электрических устройств представляет резонанс напряжений? Где используется резонанс напряжений? Ответ10. При резонансе напряжения на емкости и на индуктивности равны  и могут значительно превышать подводимое напряжение U, если и значительно превышают R:, .Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробоя изоляции. В тоже время, резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике, в различных приборах и устройствах, основанных на резонансных явлениях. Радиоприемники настраиваются на волну( частоту) радиостанции путем изменения емкости. При резонансе, частота передающей станции и частота контура LC совпадают, что приводит к значительному усилению только этого сигнала на входе приемника. Отношение XC /R может достигать 104 и поэтому напряжение на емкости UC будет больше входного сигнала антенны U во столько же раз. Тема №3. ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ ФАЗ НАГРУЗКИ «ЗВЕЗДОЙ» Цель работы: 1) ознакомиться с трехфазной цепью переменного тока и ее основными режимами работы при соединении фаз приемника «звездой» 2) по опытным данным выяснить влияние нейтрального провода на работу трехфазной цепи; 3) усвоить методику построения векторных диаграмм для основных режимов работы; 4) изучить способы измерения напряжений, токов и активной мощности цепи. Приборы и оборудование Исследование трехфазной цепи проводится на универсальном стенде (см. рис.16), где имеется нагрузка в виде трех ламповых реостатов (активная нагрузка). Для измерения величины токов и напряжений используются амперметр PA1 и вольтметр PV1с вилками. При включении амперметра PA1 в гнезда соответствующей фазы, тумблер, замыкающий эти гнезда, на время измерения ставится в положение «отключено» (SA3 для фазы a, SA5 для фазы b и SA7 для фазы c). С помощью двухэлементного ваттметра PW1 и PW2 измеряется активная мощность при трехпроводной системе включения приемников. Контрольные вопросы Вопрос1. Как обозначаются зажимы трехфазного источника и приемника? Ответ1. Большими буквами А,В,С и X,Y,Z обозначают начала и концы обмоток генератора. Концы и начала сопротивлений нагрузки обозначают малыми буквами a,b,с и x,y,z соответственно. Вопрос2. Как соединяются электроприемники «звездой»? Ответ2. Существуют 2 варианта соединения приемника и генератора по схеме звезда: а) трехпроводная и б) 4-х проводная или схема соединения с нейтральным проводом. Для соединения фаз приемника «звездой» без нейтрального провода, концы сопротивлений фаз приемника (x, y, z) соединяют в одну общую точку n, называемую нулевой, или нейтральной точкой приемника (рис.2а), начала фаз приемника (a, b, c) присоединяют к проводам, идущим к соответствующим фазам генератора (A, B, C). Эти провода называются линейными. Для соединения фаз приемника «звездой» с нейтральном проводом, к предыдущей схеме добавляют провод, соединяющий нейтральную точку нагрузки n и нейтральную точку генератора N. (рис.2б).Этот провод называют нейтральным или нулевым. 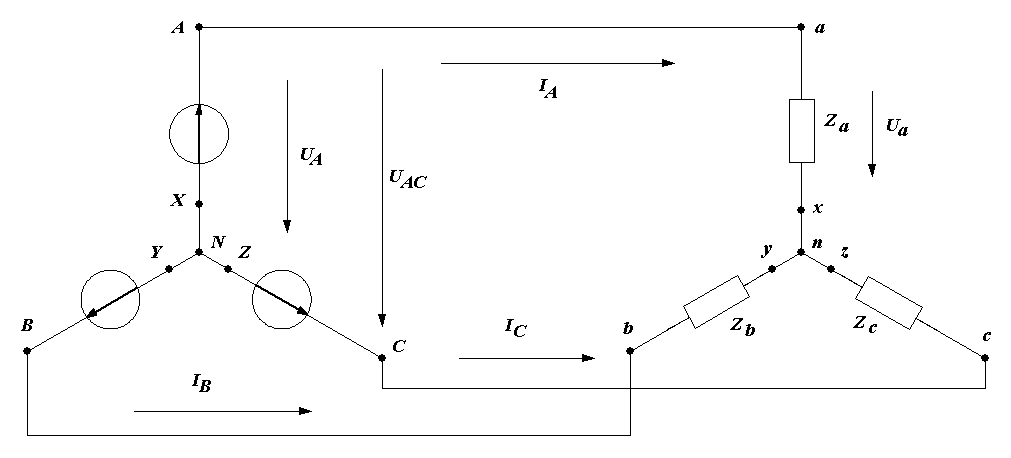 рис 2 а 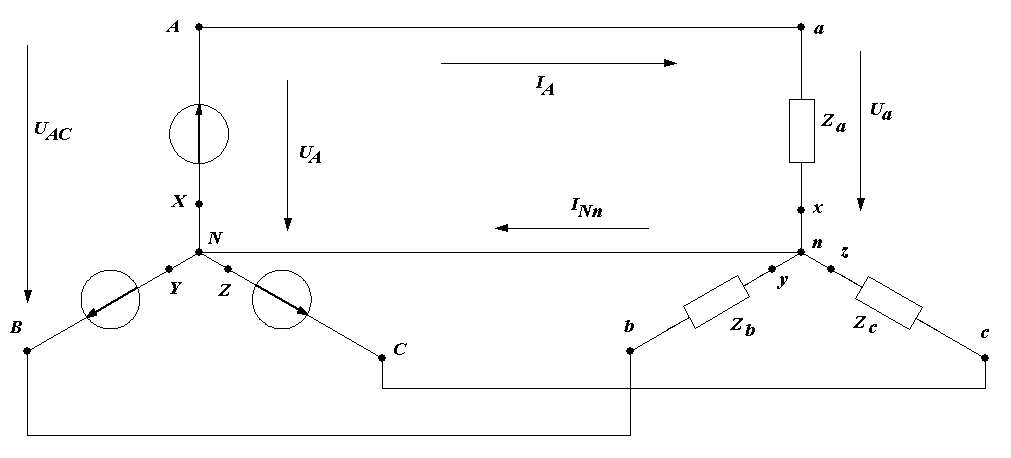 рис 2 б Вопрос3. Какими уравнениями выражаются мгновенные значения фазных напряжений и токов при симметричной нагрузке? Ответ3. Закон изменения и соответствующие графики мгновенных значений ЭДС на клеммах генераторов можно представить в виде уравнений (3-1а,б,в) и рис.3.1 соответственно : u(t)A= UmSinωt (3.1а) u(t)B= UmSin(ωt+2π/3) (3.1б) u(t)C= UmSin(ωt+4 π/3) (3.1в) 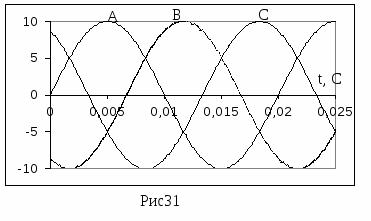 Случай 4-х проводной схемы соединений. При наличии нейтрального провода фазные напряжения приемника становятся равными фазным напряжениям источника ŮA=Ů а ; ŮВ =Ůb; ŮC =Ůc . Закон изменения мгновенных значений падений напряжений на клеммах фаз приемника в случае 4-х проводной схемы соединения совпадает с законом изменения фазных напряжений на клеммах генератора, при этом в случае если внутреннее сопротивление генератора Zвн=0, то закон совпадает с законом изменения ЭДС генератора. Уравнения (3-2 а,б,в) соответственно : u(t)A= u(t)а= UmSinωt (3.2а) u(t)B =u(t)b= UmSin(ωt+2π/3)= UmSin(360/T. t+120°) (3.2б) u(t)C =u(t)c= UmSin(ωt+4 π/3)= UmSin(360/T. t+240°) (3.2в) Закон изменения мгновенных значений токов в нагрузке при несимметричной нагрузке следует из закона Ома. Уравнения (3-3 а,б,в) соответственно : i(t)а= UmSinωt/ Zа = Um/Zа· Sin[ωt- φа] (3.3а) i(t)b= UmSin(ωt+120°)/ Zb = Um/Zb· Sin[ωt +120°- φb] (3.3б) i(t)C= UmSin(ωt+240°)/ Zc = Um/Zc · Sin[ωt+ 240°- φc] (3.3в) где: φа= arctg(JmŻа/ReŻа); φb= arctg(JmŻb/ReŻb); φc= arctg(JmŻc/ReŻc). При симметричной нагрузке Zа= Zb =Zc соответственно : φа= φа= φа = arctg(JmZа/ReZа). i(t)а= UmSinωt/ Zа = Um/Zа· Sin[ωt - φа] (3.4а) i(t)b= UmSinωt/ Zа = Um/Zа· Sin[ωt+120°- φа] (3.4б) i(t)c= UmSinωt/ Zа = Um/Zа· Sin[ωt+240°- φа] (3.4в) Ток в нейтральном проводеравен сумме мгновенных значений фазных токов: i(t)Nn =i(t)а+ i(t)b +i(t)b (3.4г) При симметричной нагрузке ток в нейтральном проводе i(t)Nn =0 (3.4д) Вывод: 1.При симметричной нагрузке Zа=Zb=Zc, соответственно: φа=φа=φа= arctg(JmZа/ReZа). 2. Ток в нейтральном проводе равен нулю !!! Случай 3-х проводной схемы соединений. При симметричной нагрузке закон изменения мгновенных значений падений напряжения на клеммах фаз приемника совпадает с законом изменения фазных напряжений на клеммах генератора, при этом в случае, если внутреннее сопротивление генератора Zвн=0, то закон совпадает с законом изменения ЭДС генератора. Уравнения (3-2 а,б,в) соответственно. Мгновенные значения токов в нагрузке при симметричной нагрузке ( по закону Ома). соответственно равны: i(t)а= UmSinωt/ Zа = Um/Zа· Sin[ωt- φа] (3.3а) i(t)b= UmSin(ωt+2π/3)/ Zb = Um/Zа· Sin[ωt +120°- φb] (3.3б) i(t)C= UmSin(ωt+4π/3)/ Zc = Um/Zа · Sin[ωt+ 240°- φc] (3.3в) где:φа,b,c= arctg(JmŻа/ReZа,b,c). Вопрос4. В каком соотношении находятся линейные и фазные напряжения при симметричной нагрузке? Ответ4. При симметричной нагрузке в случае 3-х и 4-х проводной схем соединений  . ***)При соединении фаз нагрузки «звездой» линейные токи одновременно являются и фазными, поэтому  .Вопрос5. Какой режим работы трехфазной цепи называют несимметричным? Ответ5. При несимметричной нагрузке комплексы сопротивлений фаз нагрузки не равны Zа≠Zb≠Zc, Вопрос6. Для чего используется нейтральный провод? Ответ6. Нейтральный провод используется для выравнивания фазных напряжений на клеммах нагрузки . ŮA=Ů а ; ŮВ =Ůb; ŮC =Ůc. В этом случае, падения напряжения на нагрузке остаются равными фазным напряжениям генератора. В случае, если внутреннее сопротивление генератора пренебрежимо мало ( равно нулю ), напряжения на нагрузке остаются равными фазным напряжениям генератора, постоянными и не зависят от величины нагрузки. (Ток будет изменяться, а напряжение на нагрузке не изменится). Вопрос7. Какими уравнениями описывается электрическое состояние цепи при несимметричной нагрузке? Ответ7. При несимметричной нагрузке фаз и отсутствии нейтрального провода фазные комплексы напряжения на нагрузке  ,  ,  связаны с соответствующими комплексами напряжений источника ŮA ,ŮВ , ŮС уравнениями Кирхгофа : ;  ;  ;где  -комплексное напряжение между нейтральными точками нагрузки и источника (сети). называют напряжением смещения нейтрали.Напряжение смещения нейтрали рассчитывается методом 2-х узлов:  где : Ė– комплексные ЭДС, ġ- комплексы проводимости фаз нагрузки. Токи фаз нагрузки находят по закону Ома: İa=Ůa/Za = (ŮA - )/Za; İb=Ůb/Zb = (ŮB - )/Zb;İa =Ůc/Zc = (ŮC - )/Zc. Вопрос8. Как построить совмещенные векторные диаграммы напряжений и токов для исследованных режимов трехфазной цепи? Ответ8. Построение векторных диаграмм начинаем с векторов линейных напряжений, задаваемых сетью и от условий опыта не зависящих. Это равносторонний треугольник образованный векторами линейных напряжений. Длина вектора соответствует линейному напряжению, а углы между векторами соответствуют сдвигу фаз между векторами напряжений. 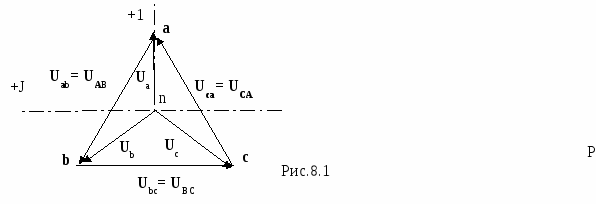 Построение векторной диаграммы для случая равномерной нагрузки.( симметричный режим). 1.Выбираем комплексную плоскость (+1,j). Реальную ось +1 направляем вертикально вверх, мнимую- вдоль оси -Х. ( поворот на угол +90°). 2. Выбираем масштаб напряжений, например 1см→20В. Вектор Ua (в масштабе) откладываем вдоль реальной оси +1.Конец вектора обозначаем малой буквой а. 3.Вектора Ub и Uc (в масштабе) рисуем под углами +120° и –120° соответственно. Концы векторов обозначаем малыми буквами b и c соответственно. 4. Точку, соответствующую, началу координат, обозначим малой буквой n. Это точка нейтрали приемника. 5.Строим вектора линейных напряжений. Для этого соединяем концы фазных векторов. Получим вектора Uab= UAB , Ubc= UBC, Ucа= UCА. Отметим, что линейные напряжения приемника равны линейным напряжениям генератора. Точка N на векторной диаграмме, соответствующая нейтральной точке генератора, находится в центре треугольника линейных напряжений. В данном случае нейтраль генератора N совпадает с нетралью приемника n. В общем случае точку n, соответствующую нейтральной точке нагрузки, находят методом засечек. Векторы токов откладывают по отношению к соответствующим векторам фазных напряжений с учетом сдвига фаз между ними. Ниже приведены векторные диаграммы для различных режимов работы. Режим1. Равномерная нагрузка без нейтрального провода ( Рис 8.1.1). 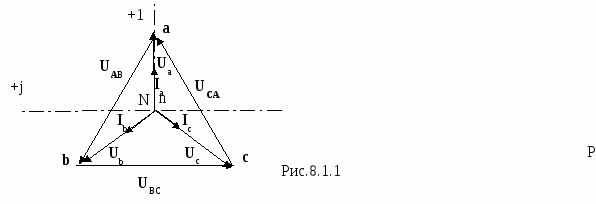 Режим 2. Обрыв фазы А( Рис 8.1.2): При обрыве фазы А и одинаковой нагрузке двух других фаз, нейтральная точка приемника n переместится на середину линейного напряжения ŮBC .Сопротивления Zb и Zc окажутся соединенными последовательно и включенными на линейное напряжение ŮBC. Падение напряжения между точками А и n увеличится, а фазные напряжения Ůb и Ůc станут равными половине линейного ŮBC. 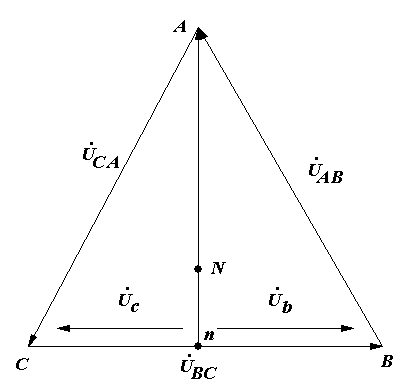 Рис 8.1.2 обрыв фазы Режим 3. Короткое замыкание фазы А( Рис 8.1.3). При замыкании фазы А и одинаковой нагрузке двух других фаз (то есть при соединении начала нагрузки фазы А с нулевой точкой нагрузки) точка n перемещается в точку А. Фазное напряжение Ůа становится равным нулю, ток İa увеличивается, а фазные напряжения Ůb и Ůc становятся равными линейным. 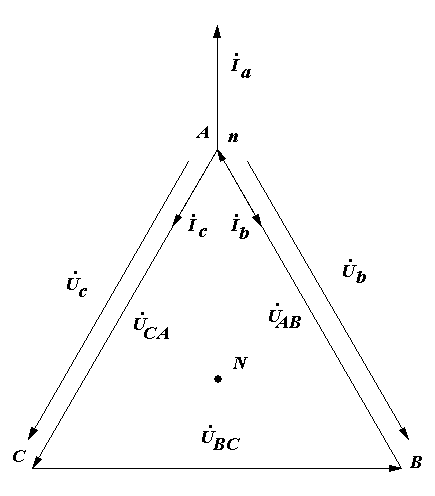 Рис 8.1.3 короткое замыкание Режим 4. Неравномерная нагрузка без нейтрального провода( Рис 8.1.4). Сопротивления, Zа≠Zb≠Zc, фазные напряжения приемника Ůа ≠Ůb ≠Ůc, между точками N и n появляется напряжение смещения нейтрали. 4.1Вначале строим треугольник линейных напряжений. 4.2. Методом засечек( циркулем или линейкой) из каждой вершины откладываем соответствующие вектора фазных напряжений приемника. Точка пересечения дуг даст точку нейтрали приемника n. Точку нейтрали генератора N оставляем на прежнем месте. 4.3 Соединяем точку n и N . Это вектор напряжения смещения нейтрали UnN ( в масштабе). 4.4 Строим вектора фазных токов нагрузки. В случае, если нагрузкой являются лампочки, которые можно представить как активные сопротивления , то сдвига фаз между фазным напряжением и фазным током нагрузки не будет. Поэтому вектора токов откладываем ( в масштабе) вдоль соответствующих векторов фазных напряжений. ***) В общем случае надо определить сдвиги фаз между током и соответствующим фазным напряжением по закону Ома в комплексной форме и строить вектор тока с помощью транспортира. 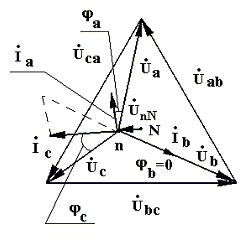 Рис 8.1.4 Неравномерная нагрузка Режим 5. Неравномерная нагрузка с нейтральным проводом(Рис 8.1.5). При наличии нейтрального провода фазные напряжения приемника становятся равными фазным напряжениям источника ŮA=Ů а ; ŮВ =Ůb; ŮC =Ůc : 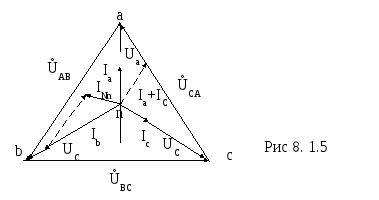 Вопрос9.. К чему приведет обрыв нейтрального провода при несимметричной нагрузке? Ответ9. Обрыв нейтрального провода при несимметричной нагрузке приведет а) к появлению напряжения смещения нейтрали, б) к неравенству фазных напряжений приемника ( и токов в фазах нагрузки). ŮA≠Ů а ; ŮВ ≠Ůb; ŮC ≠Ůc Ů а ≠Ůb ≠Ůc; İa≠ İb≠İc. Вопрос10. Как изменяется напряжение при обрыве одной фазы в четырехпроводной и трехпроводной сетях? Ответ10 а) При обрыве одной фазы ( например,обрыв фазы «а» в четырехпроводной сети, фазные напряжения Ůа,Ůb,ŮC останутся прежними, а ток в нейтральном проводе изменится: İNn= İb + İc, (Ia=0) б) При обрыве одной фазы ( например обрыв фазы «а» в трехпроводной сети, фазные токи и напряжения изменятся, при этом независимо от предыдущего состояния цепи токи будут равны : 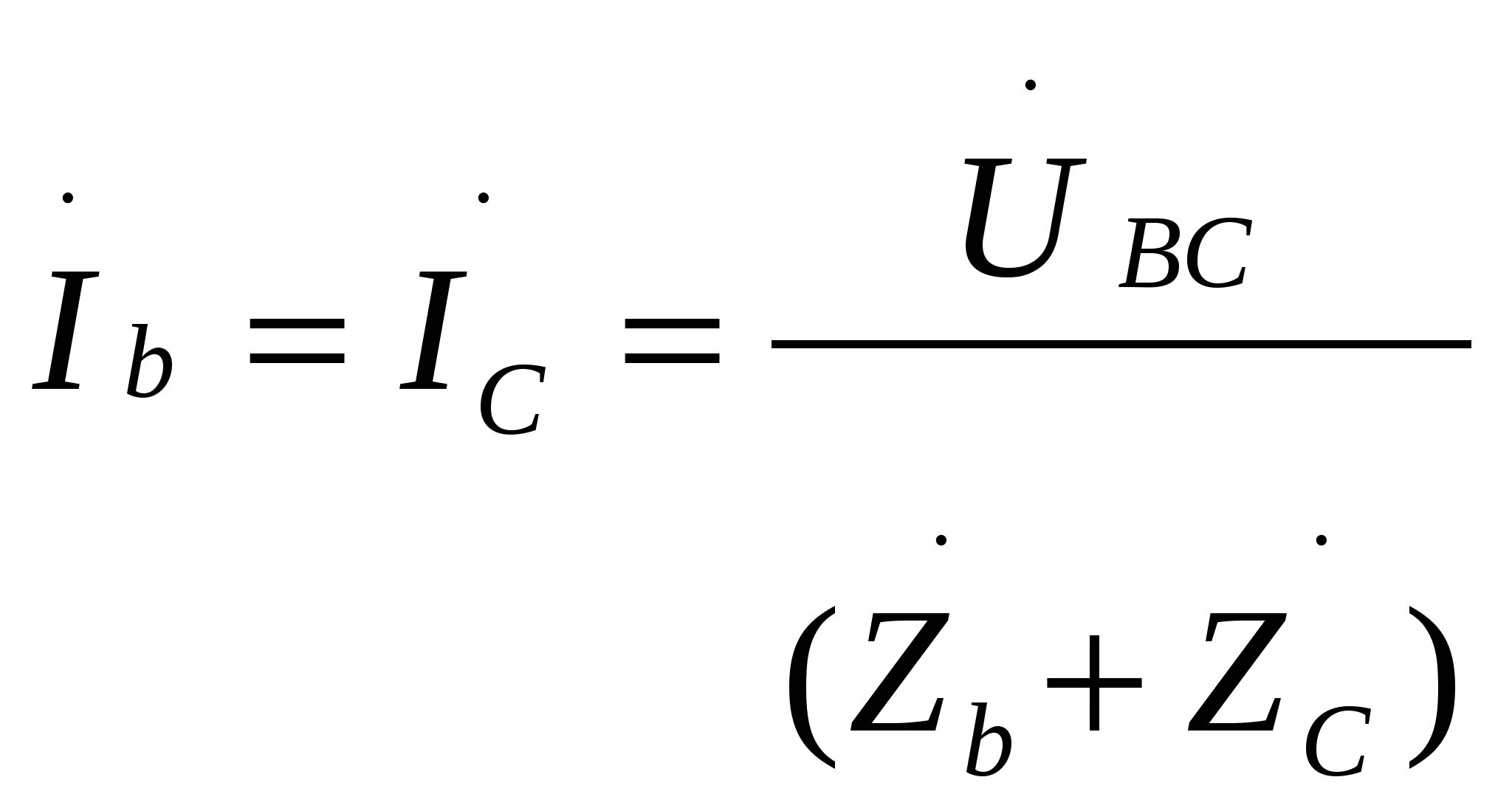 напряжения будут равны : Ůb= İb·Żb ; Ůc= İb·Żc , Ůа= ŮА- ŮNn В случае если Żb= Żc, то: Ůb= Ůc= ŮBC/2, Uа= √3/2 ·UBC=3/2 ·UФ Вопрос11. а) Как изменяется напряжение при коротком замыкании фазы в трехпроводной сети? б)К чему приведет короткое замыкание фазы в четырехпроводной сети? Ответ11 1. .Короткое замыкание фазы( например фазы «а») в трехпроводной сети приведет к: 1). Фазное напряжения Uа =0. 2)При замыкании фазы «а» и одинаковой нагрузке двух других фаз (то есть, при соединении начала нагрузки фазы А с нулевой точкой нагрузки) точка А перемещается в точку n.( рис 11.1) Фазное напряжение Ůа становится равным нулю, ток İa увеличивается, а фазные напряжения Ůb и Ůc становятся равными линейным. При этом вектора UC и UCА будут параллельны, а вектора Ub и UAB будут направлены встречно, Ub = ─ UAB , UC = UCА Рис 11.1 Ответ11 2. Короткое замыкание фазы( например фазы «b») в четырехпроводной сети приведет: 1) К замыканию генератора фазы «b», при этом ток короткого замыкания будет ограничен только внутренним сопротивлением генератора фазы «В» Zint.  и сопротивлением линейного и нейтрального проводов.2) Фазное напряжения Ub станет равным 0. 3) Фазные напряжения Uа и Uc нагрузок не изменятся. Вопрос12. К чему приводит обрыв линейного провода в трехфазной установке а)четырехпроводной и б)трехпроводной систем? Ответ12 а) В четырехпроводной системе – к изменению тока в нейтральном проводе. Напряжения не изменяются. б) В трехпроводной системе при обрыве фазы А сопротивление Zb и Zc окажутся соединенными последовательно и включенными на линейное напряжение ŮBC. Разность потенциалов между А и n увеличится, а фазные напряжения Ůb и Ůc станут равными половине линейного ŮBC. Вопрос13. Как измеряют мощность трехфазной несимметричной нагрузки в четырехпроводной системе? Ответ13. В этом случае применяют три однофазных ваттметра, каждый из которых подключается на соответствующее фазное напряжение и соответствующий фазный ток. Активная мощность системы равна алгебраической сумме показаний трех ваттметров. 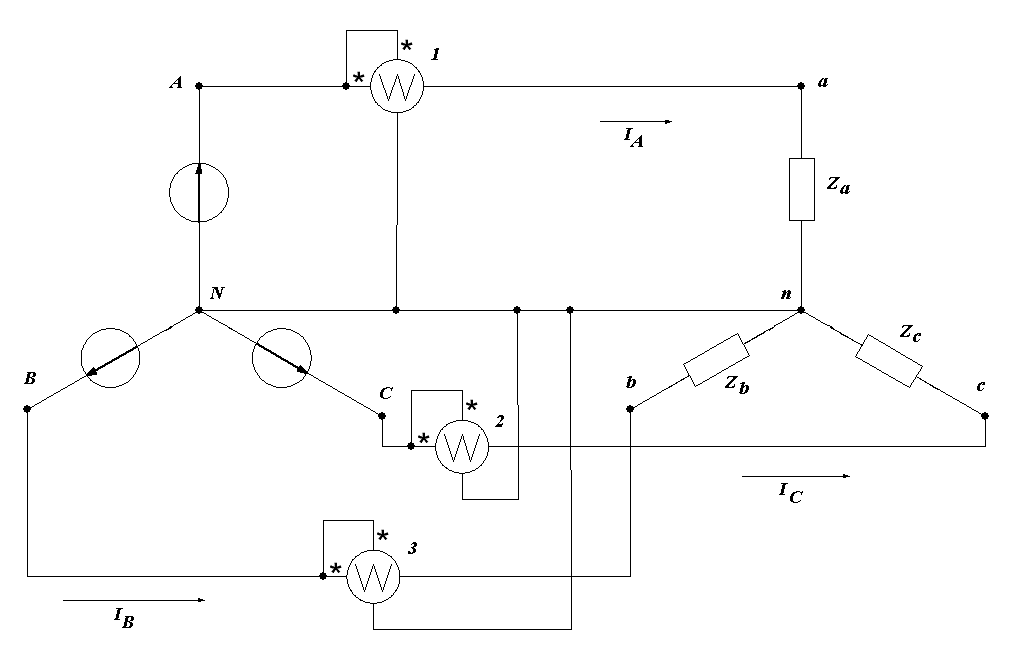 Рис Вопрос14. В каких случаях используется метод измерения мощности двумя ваттметрами? Ответ14. Этот метод применяют при несимметричной нагрузке без нейтрального провода. Сумма ( алгебраическая) показаний двух ваттметров при этом определяет активную мощность всей системы независимо от того, в звезду или треугольник соединена нагрузка. ***)треугольник нагрузки всегда может быть преобразован в эквивалентную звезду. 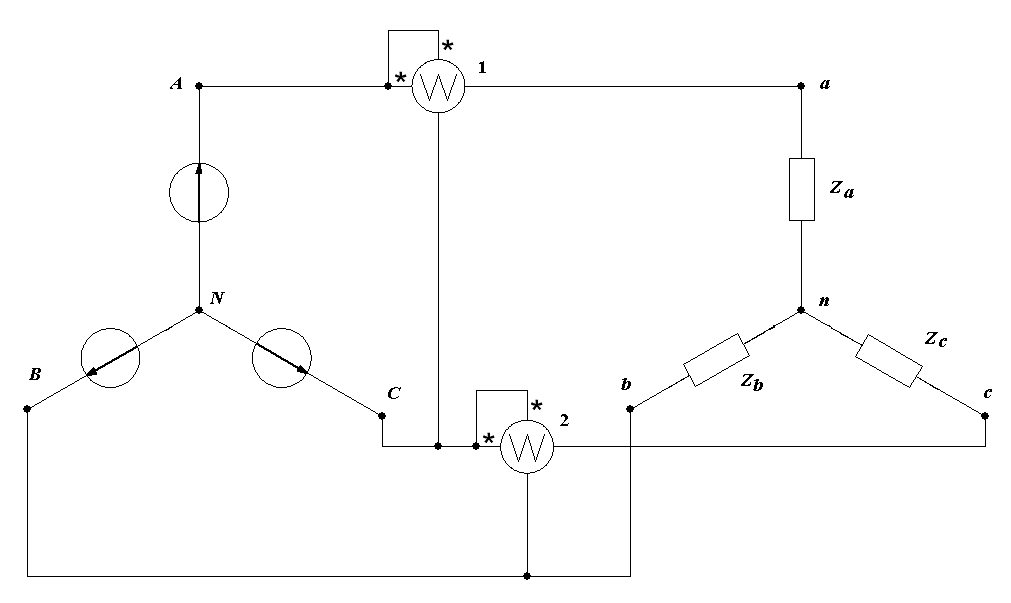 Рис 14. Вопрос15. Написать уравнения для активной, реактивной и полной мощностей при симметричной и несимметричной нагрузках. Ответ15. |
.