Методические указания для студентов очной и заочной форм обучения по специальности 120700 Землеустройство и кадастры
 Скачать 0.53 Mb.
|
|
Министерство сельского хозяйства Российской Федерации Департамент научно-технологической политики и образования ФГБОУ ВПО «Красноярский государственный аграрный университет» ОБРАБОТКА МАТЕРИАЛОВ ТЕОДОЛИТНОЙ СЪЕМКИ Методические указания для студентов очной и заочной форм обучения по специальности 120700 «Землеустройство и кадастры» Красноярск, 2012 Рецензент Попов В.П. канд. с.-х. наук, профессор кафедры землеустройства Института землеустройства, кадастров и природообустройства Красноярского государственного аграрного университета Самошина, Т.Ю. ОБРАБОТКА МАТЕРИАЛОВ ТЕОДОЛИТНОЙ СЪЕМКИ: Метод. указания / Т.Ю. Самошина, Краснояр. гос. аграр. ун–т. – Красноярск, 2012. – 23 с. Методические указания предназначены для лабораторных занятий студентам очной формы обучения и выполнения контрольной работы студентам заочной формы обучения специальности 120700 «Землеустройство и кадастры» и соответствуют типовой программе курса «Геодезия» для высших учебных заведений. Печатается по решению редакционно-издательского совета Красноярского государственного аграрного университета © Самошина Т.Ю. Красноярский государственный аграрный университет, 2012 ОБЩИЕ СВЕДЕНИЯМетодические указания подготовлены в соответствии с рабочей программой и соответствуют типовой программе по курсу «Геодезия» для студентов очной и заочной формы обучения по специальности 120700 «Землеустройство и кадастры». В методическом указании описана поэтапная обработка материалов теодолитной съемки и построение плана. Исходные данные: - общая схема теодолитных ходов (рис. 1), на которой даны измеренные правые по ходу углы и горизонтальные проложения линий; - абрис со всеми данными (рис. 3а, 3б);
Таблица 1 – Исходные данные
где N – последние две цифры номера зачетной книжки 1. Камеральная обработка замкнутого хода (полигона) 1) Определение угловой невязки. В первую графу таблицы 2 записывают по порядку номера всех вершин замкнутой фигуры, а во вторую графу со схемы (рис. 1) размеры этих углов (измеренные). Напротив точки I записывают примычные в право по ходу лежащие углы, соединяющие исходную сторону с последующей. Все измеренные величины внутренних углов складывают и получают и их сумму (  ) которую подписывают внизу второй графы под общей чертой. Полученную сумму сравнить с теоретической суммой ( ), определенной по формуле , (1)где n - число углов полигона; 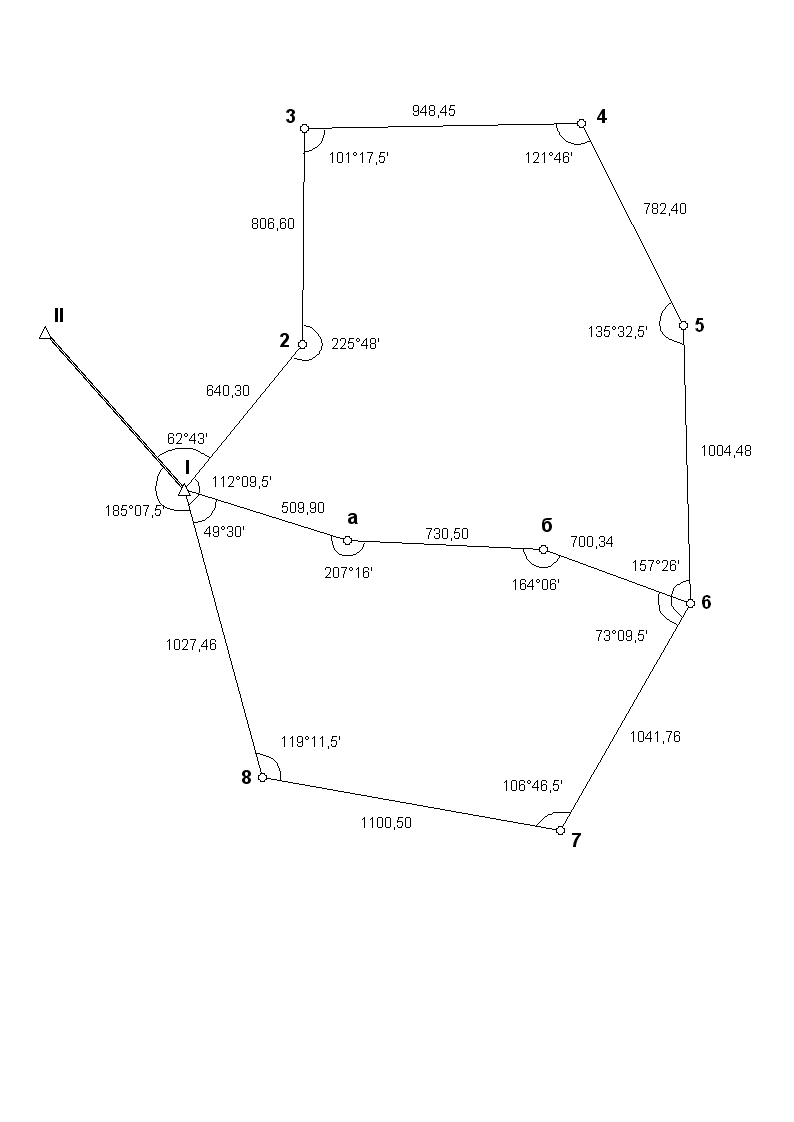 Рисунок 1 – Схема теодолитных ходовТак в рассматриваемом примере для восьмиугольника теоретическая сумма внутренних углов должна быть равна:  а сумма углов, полученных в результате измерения, оказалась равной 1079°57',5 т. е. получилось расхождение или угловая невязка. Для определения абсолютного значения невязки и ее знака используем следующую формулу:  (2)Полученное значение также заносится в ведомость. Полученная угловая невязка не должна превышать допустимой величины, определяемой по формуле:  (3)Из формулы ясно, что допустимая угловая невязка для восьмиугольного полигона не должна превышать значения  В нашем примере угловая невязка равна -2'.5, следовательно, она допустима, а поэтому должна быть распределена по отдельным углам. Следующим шагом является распределение угловой невязки. Для этого она по частям вводится в виде поправок в измеренные углы: либо поровну во все измеренные углы, либо в углы с дробными долями минут, чтобы округлить их до целых минут, либо в углы, ограниченные более короткими сторонами. Знак этой поправки берется обратным знаку полученной невязки. В нашем примере знак поправки должен быть плюс, потому что сумма измеренных углов меньше теоретической. Поправки с их знаками выписываются над значениями соответствующих измеренных углов. Сумма поправок должна равняться невязке с обратным знаком. А сумма исправленных углов должна равняться сумме углов теоретической. 2) Вычисление дирекционных углов По исходному дирекционному углу (αI-II) соответствующего варианта и исправленным углам вычисляются дирекционные углы всех других сторон основного хода по формуле  (4)Если в процессе вычислений дирекционный угол какой-либо стороны окажется больше 360°, то от полученного значения нужно вычесть 360°, а при получении отрицательного значения – прибавить 360°. Таблица 2 – Ведомость вычисления координат замкнутого полигона
В результате последовательного вычисления дирекционных углов сторон полигона должен получиться обратный дирекционный угол исходной стороны полигона (αI-II). Прямой дирекционный угол отличается от обратного на 180°. 3) Перевод дирекционных углов в румбы Вычисленные дирекционные углы переводят в румбы. Для этого необходимо воспользоваться зависимостью дирекционных углов и румбов из таблицы 3. Таблица 3 – Зависимость дирекционных углов и румбов
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
αII-I
ƒх2 + ƒу2 =