Методические указания_Начертательная геометрия. Методические указания и контрольные задания для студентов заочников строительных специальностей вузов
 Скачать 8.53 Mb. Скачать 8.53 Mb.
|
|
Задача 1. Дано: плоскость треугольника (А, В, С) и точка D. Требуется определить расстояние от точки D до плоскости, заданной треугольником (А, В, С). Определить видимость перпендикуляра, проходящего через точку D, и плоскости треугольника(А, В, С). Данные для выполнения задачи взять из та6л. 3, в соответствии с вариантом. Указания к задаче 1. Задачу выполняют в такой последовательности: 1) из точки D опустить перпендикуляр, используя горизонталь h и фронталь f плоскости. При этом горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали h1, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали f2; 2) определить точку пересечения перпендикуляра с плоскостью (А, В, С), для чего перпендикуляр (прямую) заключают во вспомогательную, обычно проецирующую, плоскость (γ), находят линию пересечения плоскости (А, В, С) и вспомогательной и отмечают точку К, в которой эта линия пересекается с перпендикуляром; 3) определяют натуральную величину (Н.В.) расстояния от точки D до плоскости (А, В, С), применяя способ прямоугольного треугольника; 4) видимость проекции перпендикуляра определяют методом конкурирующих точек. Таблица 4
Задача 2. Дано: плоскость треугольника (А, В, С). Требуется: построить плоскость, параллельную заданной и отстоящую от нее на 45...50 мм. Данные для выполнения задачи взять в табл. З. Указания к задаче 2. Задачу выполняют в такой последовательности: 1) в заданной плоскости (А, В, С) выбирают произвольную точку (в том числе вершину, на рис. 8 взята точка С) и из неё восстанавливают перпендикуляр к плоскости (А, В, С), аналогично действию в первой задаче. В связи с тем, что задачи 1 и 2 совмещены на одном чертеже и направление перпендикуляра к плоскости (А, В, С) уже выявлено - прямая b(D, К), то перпендикуляр через произвольно выбранную точку можно провести как прямую, параллельную перпендикуляру b(D, К). На эпюре одноименные проекции параллельных прямых параллельны; 2) определяют методом прямоугольного треугольника натуральную величину произвольного отрезка перпендикуляра, который ограничивают произвольной точкой Р; 3) на натуральной величине произвольного отрезка перпендикуляра находят точку Т, расположенную на заданном расстоянии 4...5 мм от плоскости, и строят проекции этой точки на проекциях перпендикуляра; 4) через точку Т строят искомую плоскость, соблюдая условие параллельности плоскостей: если плоскости параллельны, то две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На эпюре одноименные проекции пересекающихся прямых параллельны. Задача 3. Дано: плоскость треугольника (А, В, С) и прямая а (D, Е). Требуется: через прямую а (D, Е) провести плоскость, перпендикулярную плоскости треугольника (А, В, С), построить линию пересечения этих двух плоскостей, определить видимость. Данные для выполнения задачи взять из табл. 3. Указания к выполнению задачи 3. Задача содержит следующие действия: 1) строят плоскость, перпендикулярную плоскости (А, В, С). Плоскость, перпендикулярная другой плоскости, должна проходить через перпендикуляр к этой плоскости. Искомая плоскость, перпендикулярная плоскости (А, В, С), должна содержать в себе заданную прямую а (D, Е) и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость (А, С, В); (например, из точки В); 2) строят линию пересечения двух плоскостей: заданной плоскостью треугольника (А, В, С) и построенной, перпендикулярной ей. Задачу на определение линии пересечения двух плоскостей можно решить двумя способами: первый - построить точки, пересечения двух прямых одной плоскости с другой плоскостью, т. е. использовать два раза схему нахождения точки пересечения прямой с плоскостью; второй - ввести две вспомогательные секущие плоскости частного положения, которые одновременно пересекали бы плоскость (А, В, С) и плоскость, перпендикулярную ей, построить на линии пересечения с заданными плоскостями. Две собственные точки пересечения этих линий определяют линию пересечения данных плоскостей. В примере выполнения листа 4 (рис. 8) в задаче 3 применен первый способ. Точки пересечения прямой а (В, Е) и перпендикуляра b (D, К) определяют линию пересечения плоскостей (А, В, С) и искомой перпендикулярной к ней; 3) определяют видимость пересекающихся заданных плоскостей. Видимость плоскостей устанавливают с помощью конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям. При решении задач 1, 2, 3 нужно помнить следующие положения ортогональных проекций, 1. Две проекции точки определяют ее положение в пространстве (относительно плоскостей проекций), так как по двум проекциям можно установить расстояние от точки до всех трех основных плоскостей проекций. 2. Ортогональные проекции одной и той же точки располагаются на перпендикуляре к оси проекции, который называется линией связи. 3. Если одна проекция прямой параллельна оси проекции, то такая прямая параллельна одной из плоскостей проекций, Принадлежащий ей отрезок проецируется на одну плоскость в натуральную величину (горизонтальная, фронтальная, профильная прямые). Если обе проекции прямой параллельны одной из осей проекций, то такая прямая занимает проецирующее положение, Одна из ее проекций вырождается в точку. 4. Проекция отрезка прямой общего положения всегда меньше отрезка в натуре. 5. Одноименные проекции параллельных прямых взаимно параллельны. 6. Точки пересечения одноименных проекций пересекающихся прямых расположены на одной и той же линии связи. Точки пересечения одноименных проекций скрещивающихся прямых не расположены на одной и той же линии связи. 7. Прямой угол проецируется на плоскость также в прямой угол, если одна его сторона параллельна этой плоскости. 8. Горизонталь, фронталь и линии наклона плоскости являются главными линиями плоскости. Фронтальная проекция горизонтали параллельна оси Х, горизонтальная проекция параллельна горизонтальному следу плоскости. Горизонтальная проекция фронтали параллельна оси Х, фронтальная проекция - фронтальному следу плоскости. Линии наклона плоскости перпендикулярны фронталям, горизонталям или профильным прямым плоскости. Угол их наклона к соответствующей плоскости проекций определяет угол наклона плоскости к той же плоскости проекций. 9. Линия пересечения любой плоскости с горизонтальной плоскостью является горизонталью, с фронтальной - фронталью. Лист 5 Формат АЗ. Основная надпись по форме 4а. Выполнить две задачи на способы преобразования проекций. Пример выполнения листа представлен на рис. 9. Задача 1. Дано: треугольник АВС. Требуется: способом вращения вокруг осей, перпендикулярных плоскостям проекций, определить величину треугольника АВС. данные для выполнения задачи берут из табл. 5. 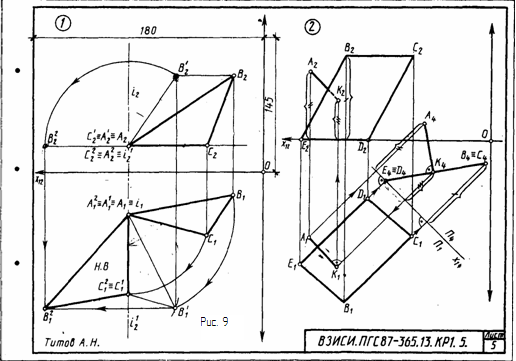 Указания к задаче 1. Соблюдая правила вращения геометрических фигур вокруг оси, перпендикулярной плоскости проекций, необходимо выполнить два действия: 1) привести треугольник АВС в положение проецирующей плоскости, т. е. перпендикулярной плоскости проекций. Признаком перпендикулярности заданной плоскости плоскостям проекций на эпюре является вырождение одной из проекций плоскости треугольника (А, В, С) в прямую линию, для получения фронтально-проецирующей плоскости необходимо горизонталь плоскости (А, В, С) вместе с системой всех точек треугольника АВС поставить в положение, перпендикулярное фронтальной плоскости проекций, а для получения горизонтально-проецирующей плоскости необходимо фронталь плоскости (А, В, С) со всеми точками плоскости перевести в положение прямой, перпендикулярной горизонтальной плоскости проекций; 2) полученную проецирующую плоскость преобразовать в плоскость уровня, т. е. параллельную либо горизонтальной, либо фронтальной плоскости проекций, в зависимости от ее положения на первом этапе преобразования. Для этого выродившуюся в прямую линию проекцию треугольника АВС изобразить в положении, параллельном оси Х. Проекция треугольника АВС на одной из плоскостей проекций и будет являться натуральной величиной треугольника АВС. При вращении фигур вокруг осей, перпендикулярных плоскостям проекций, необходимо учитывать следующее: 1. Линия перемещения точки (траектория) представляет собой окружность. Так как плоскость траектории параллельна плоскости проекций, то проекции точки перемещаются: одна - по окружности, другая по прямой, параллельной оси проекций, 2. Проекция фигуры на ту плоскость проекций, на которой ось вращения проецируется в точку, не изменяется ни по величине, ни по форме, изменяется только е положение относительно оси проекций. З. Ось проекций не участвует в решении задач (как это имеет место при замене плоскостей проекций), поэтому на чертеж она может быть не проведена. Таблица 5
Задача 2. Дано: четырехугольник ЕВСD и точка А. Требуется: способом замены плоскостей проекций определит расстояние от точки А до плоскости ( Е, В, С, D), построить проекции этого расстояния на исходном эпюре и описать последовательность выполнений графических процедур решения задачи способом, показанным на листе З (см. рис. 7). Точки Е, В, С, D для всех вариантов имеют одинаковые координаты: Е(90, 60, 10), В(60, 90, 80), С(10, 60, 80), D(40, 30, 10). Координаты точки А берут из табл. 6. Таблица 6
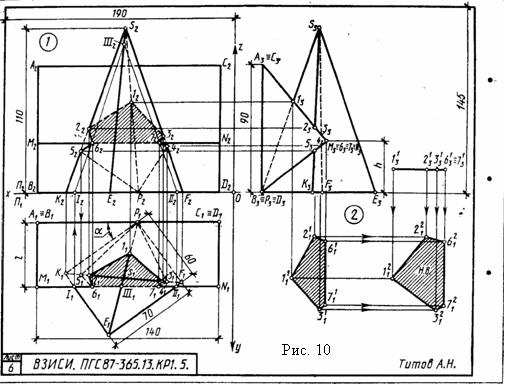
Указания к задаче 2. Соблюдая правила построения геометрических фигур на знаменных плоскостях проекций, необходимо 1) преобразовать плоскость общего положения (Е, В, С, D) в плоскость фронтально-проецирующую и построить проекцию точки А. Положение новой плоскости определяет новая ось проекций Х14, Она должна располагаться перпендикулярно горизонтальной проекции горизонтали плоскости (Е, В, С, D), 2) определить расстояние от точки А до заданной плоскости. Оно равно отрезку перпендикуляра АК, опущенного из точки А на плоскость (Е, В, С, D), выродившуюся на новой фронтальной плоскости проекций в прямую линию; 3) получив основание перпендикуляра (К4), построить его проекции на исходном чертеже задачи. Так как проекция отрезка А4К4 перпендикуляра b - натуральная величина отрезка, то, следовательно, его проекция на плоскость П1 будет параллельна оси Х14. Координату Z для плоскости П2 следует снять с плоскости проекций П4; 4) описание последовательности графических процедур при решении задачи выполнять по аналогии с примером, приведенным на рис. 7. При изучении способа замены плоскостей нужно иметь в виду, что фигура не меняет своего положения в пространстве, плоскость же проекций П1 или П2 заменяют плоскостью, соответственно П5 или П4. Такую замену проводят последовательно, сначала заменяют одну плоскость, затем другую. При построения проекции фигуры на новой плоскости проекций необходимо помнить, что происходит переход от одного эпюра к другому, на котором соответственные проекции точек также расположены на линиях связи. Координата точки на но плоскости проекций равна координате точки на заменяемой плоскости проекций. Лист 6 Формат АЗ. Основная надпись по форме 4б. Выполнить две задачи на пересечение многогранных поверхностей и определение натуральной величины сечения многогранника плоскостью. Пример выполнения листа на рис. 10. Задача 1. Дано: прямая четырехгранная пирамида и трехгранная горизонтальная призма. Требуется: вычертить три проекции пирамиды и призмы, построить линию пересечения этих многогранников и определить ее видимость, для всех вариантов стороны основания пирамиды Р1F1 = К1Е1 = 60 мм; К1Р1=Е1F1=70 мм; высота пирамиды 110 мм; высота вертикальной грани призмы 90 мм; длина всех ребер призмы 140 мм (рис. 10). Величины l, h, <, а также значения координат точек Р и D берут из табл. 7 в соответствии с номером варианта. Таблица 7
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
