Методические указания_Начертательная геометрия. Методические указания и контрольные задания для студентов заочников строительных специальностей вузов

• Название: Методические указания и контрольные задания для студентов заочников строительных специальностей вузов
• Анкор: Методические указания_Начертательная геометрия.doc
• Дата: 28.11.2017
• Размер: 8.53 Mb.
• Имя файла: Методические указания_Начертательная геометрия.doc
• Тип: Методические указания; #10505
• страница: 4 из 9

Указания к задаче 1. Вычерчивание пирамиды нужно начинать с точки Р, а призмы - с точки D. Основание пирамиды расположено в плоскости П₁, ее ребра прямые общего положения. Одна из граней призмы - фронтальная плоскость (параллельная П₂). Две других - профильнопроецирующие, поэтому ребра этих граней на плоскости П₃ проецируются в точки.

Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линий пересечения граней многогранников. Соединяя каждые пары точек одних и тех же граней отрезками прямых, получаем линии пересечения многогранников. Видимыми линиями пересечения многогранников будут те, которые принадлежат их видимым граням. Линия пересечения многогранников строится только с использованием фронтальных и горизонтальных проекций фигур. Профильные проекции фигур применить для проверки правильности определения точек пересечения ребер с гранями и их последовательного соединения.
Задача 2. Дано: прямая четырехгранная пирамида и одна грань призмы. Требуется: способом плоскопараллельного перемещения определить натуральную величину сечения пирамиды с гранью призмы. Исходные данные берут из табл. 7.

Указания к задаче 2. Для выполнения данной задачи используют результат решения задачи 1, выделяя из него часть линии пересечения, которая относится к указанной для варианта грани по табл. 7. Профильную проекцию пирамиды с заданной секущей гранью призмы принимают за фронтальную проекцию и к ней достраивают горизонтальную проекцию сечения пирамиды гранью по уже имеющейся горизонтальной проекции в задаче 1, но соответственно развернув его в проекционной связи (см. рис. 10). Так как секущая грань занимает положение проецирующей плоскости то, чтобы получить натуральную величину сечения, достаточно произвести одно перемещение. Способом плоскопараллельного перемещения проецирующую плоскость грани ставим в положение плоскости уровня (параллельное горизонтальной плоскости проекций).

При способе плоскопараллельного перемещения все точки фигуры перемещаются в плоскостях, параллельных какой-либо одной плоскости проекций. Поэтому проекция траекторий точек на вторую плоскость проекций представляют собой прямые линии, параллельные оси проекций. Как и про вращении вокруг осей, перпендикулярных плоскостям проекций, при плоскопараллельном перемещении одна проекция фигуры не меняется ни по величине, ни по форме.
КОНТРОЛЬНАЯ РАБОТА 2

(Листы 7...12. Листы 8, 10, 12 соответственно выполняются на обороте листов 5, 7, 9, 11)
Лист 7

Формат АЗ. Основная надпись по форме 4а. Выполнить три задачи на пересечение поверхности плоскостью и прямой. Пример выполнения листа на рис. 11. Задачи 1 и 2 выполняют в левой части листа, одна под другой, а задачу 3 в правой части листа.

Задача 1. Дано: пирамида и прямая l. Требуется: определить точки пересечения прямой l с поверхностью трехгранной пирамиды. Все варианты задач имеют два одинаковых параметра: высоту пирамиды 70 мм и диаметр вспомогательной окружности 60 мм, в которую вписывается треугольное основание произвольного расположения (по усмотрению студента). Положение прямой общего положения, которая пересекает пирамиду, также устанавливается студентом самостоятельно.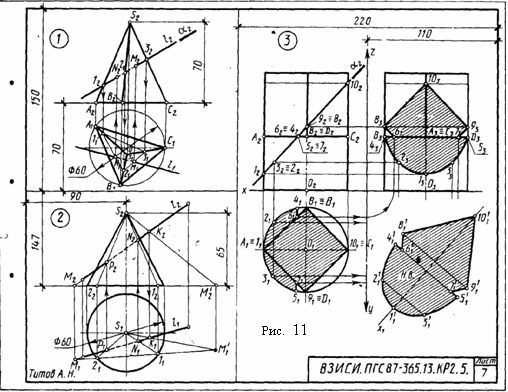



Указания к задаче 1. Чтобы решить задачу, необходимо: 1) заключить прямую во вспомогательную плоскость частного положения (фронтально - проецирующую или горизонтально - проецирующую); 2) построить линию пересечения пирамиды с этой вспомогательной плоскостью; 3) отметить точки пересечения проекций прямой с проекциями линии пересечения: 4) определить видимость

Так как плоскость, в которую заключается прямая, частного положения, то одна из проекций фигуры сечения пирамиды совпадает с проекцией секущей плоскости, выродившейся в линию. Вторую проекцию сечения достраивают по точкам фигуры сечения, которые лежат непосредственно на ребрах. Задача может иметь одно из трех решений: прямая пересекает пирамиду в двух точках, в одной точке (касается) и не пересекает поверхность.

Задача 2. Дано: основание конуса - окружность диаметра 60 мм, высота конуса 70 мм и прямая l. Требуется: определить точки пересечения прямой l с поверхностью прямого кругового конуса. Положение прямой студент выбирает самостоятельно, учитывая характеристику прямой, указанную в табл. 8.

Указания к задаче 2. Чтобы решить задачу, необходимо выполнить действия, аналогичные перечисленным в указаниях к задаче 1. При этом следует напомнить, что выбирать нужно такие вспомогательные секущие плоскости, которые дают наипростейший контур сечения конуса: окружность и треугольник. Так, например, для задачи 2, помещенной на рис. 11, вспомогательная секущая плоскость является плоскостью общего положения, которая проходит через вершину конуса и задана двумя пересекающимися прямыми (заданной прямой и произвольной прямой, проходящей через вершину конуса и точку К данной прямой). Такая плоскость дает сечение в виде треугольника. Если через горизонтальную прямую провести горизонтальную плоскость, сечение будет иметь форму окружности. После определения точек пересечения прямой с конусом не забудьте установить видимые отрезки прямой.

Таблица 8

№ варианта	Характеристика прямой l
1 2 3 4 5 6 7 8 9 0	Нисходящая общего положения Фронтальная под углом к П1 45° Горизонтально-проецирующая Горизонтальная под углом к II2 30° Фронтально-проецирующая Восходящая общего положения Горизонтальная под углом к П2 45° Фронтально-проецирующая Фронтальная под углом к П1 30° Горизонтально-проецирующая

Задача 3. Построить три проекции линии пересечения сложной поверхности с фронтально - проецирующей плоскостью и способом совмещения (вращения вокруг линии уровня) определить натуральную величину этого сечения. Данные для вычерчивания комбинированной поверхности берут и табл. 9. Таблица 9



Указания к задаче 3. Задачу размещают на правой стороне листа (см. рис. 11). Высота всей комбинированной поверхности равна 100 мм, нижняя ее часть - 35 мм. Размеры диаметров оснований поверхностей и вспомогательных окружностей, а также стороны многоугольников приведены в табл. 9. Положение секущей плоскости для своего варианта студент назначает самостоятельно. Задачу решают в два этапа: 1) строят проекции сечения; 2) определяю натуральную величин сечения указанным способом.

Так как в данном задании для пересечения предложена плоскость частного положения фронтально - проецирующая, то решение задачи сводится к построению проекций ряда точек фигуры сечения заданной поверхности как точек, расположенных на образующих или направляющих линиях этой поверхности. Первоначально крайние и промежуточные точки сечения назначаются на следу секущей плоскости. Натуральную величину сечения определяют по тем же точкам, которые были установлены на первом этапе. За ось вращения плоскости сечения выбирают фронталь плоскости сечения, совпадающую с его осью симметрии. Для того чтобы избежать наложения изображений, фронталь следует размещать на свободном поле чертежа параллельно следу секущей плоскости. Каждая точка сечения будет вращаться вокруг оси в плоскости, перпендикулярной ей. Радиус вращения отображен в натуральную величину на горизонтальной плоскости проекций и соответствует расстоянию от точки до продольной оси симметрии (оси вращения).
Лист 8

Формат АЗ. Основная надпись по форме 4 б. Выполнить две задачи на пересечение многогранных и кривых поверхностей и построение разверток поверхностей. Пример выполнения листа на рис. 12.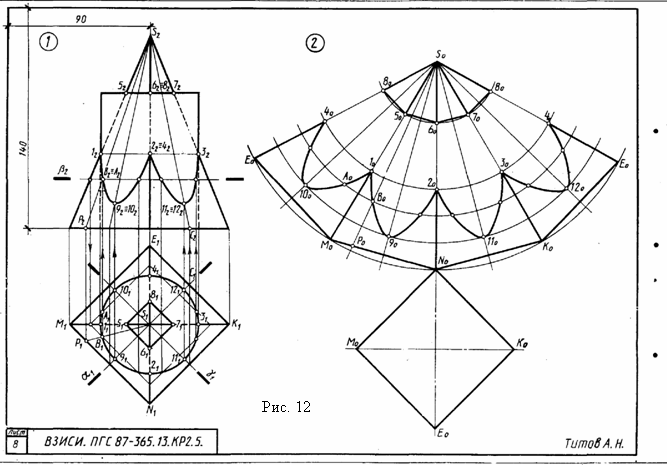



Задача 1. Дано: многогранник и кривая поверхность. Требуется: способом вспомогательных секущих плоскостей построить линию пересечения многогранной и кривой поверхностей, выделив ее видимые и не видимые участки. Данные для задачи берут из табл. 10.

Указания к задаче 1. Задачу выполняют на левой половине листа в такой последовательности: 1) намечают расположение вспомогательных секущих плоскостей частного положения (уровня) или проецирующих; 2) с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей; 3) полученные точки соединяют плавными кривыми или прямыми линиями, установив предварительно последовательность расположения точек на линии пересечения поверхностей. Видимую часть линий контура, в том числе и линии пересечения, обводят сплошной основной, а невидимую - штриховой линиями. При решении задач на взаимное пересечение поверхностей следует помнить следующие положения.

1. Чтобы построить точку, принадлежащую линии пересечения поверхностей, нужно обе поверхности рассечь вспомогательной плоскостью (иногда вспомогательной поверхностью) и, найдя линии пересечения вспомогательной плоскости с заданными поверхностями, отметить общие для них точки. Плоскость следует выбирать так, чтобы линии ее пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые). Использование нескольких вспомогательных плоскостей позволяет определить ряд точек линий пересечения. Соединять можно только те точки, которые расположены в одной грани многогранника.

2. Когда боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующее положение (образующие поверхности перпендикулярны этой плоскости проекций), то одна проекция линии пересечения поверхностей становится известной без дополнительных построений - она совпадает с проекцией поверхности.

З. Если линия, принадлежащая поверхности, видна не полностью, то точки перехода от видимой части линии пересечения к невидимой располагаются на очерке поверхности. Видимая часть линии пересечении поверхностей должна быть видимой как на одной поверхности, отдельно взятой, так и на другой.

4. Чтобы найти верхнюю или нижнюю точку линии пересечения, соответствующей грани с конусом, нужно взять такую вспомогательную плоскость, которая должна проходить через вершину конуса перпендикулярно этой грани призмы. (Для прямой призмы перпендикулярно ребрам основания)

Задача 2. Дано: две пересекающиеся поверхности - многогранник и кривая поверхность и линия их пересечения. Требуется: построить полную развертку одной из пересекающихся поверхностей и нанести на ней линию их пересечения. Поверхность для построения развертки студент выбирает сам из двух поверхностей задачи 1 в соответствии со своим вариантом.

Таблица 10


Линия пересечения поверхностей наносится по результату решения задачи 1.

Указания к задаче 2. Задачу выполняют на правой половине листа в такой последовательности; 1) в кривую поверхность вписывают многогранник; 2) определяют натуральные величины всех ребер вписанного многогранника; 3) на плоскости чертежа строят одну из граней поверхности по натуральным величинам ребер и к ней последовательно пристраивают остальные грани, пользуясь смежными ребрами; 4) соответствующие вершины граней соединяют плавными кривыми линиями.

При развертывании многогранной поверхности выполняют только вторую и третью операции. Линия пересечения поверхностей наносится на развертку с помощью ее характерных точек. Для каждой такой точки в ортогональных проекциях определяют положение образующей и направляющей линий поверхности, на пересечении которых расположена взятая точка. Строят эти линии (образующую и направляющую) на развертке и в их пересечении отмечают искомую точку линии пересечения поверхностей (рис. 12).

Лист 9

Формат АЗ. Основная надпись по форме 4 а. Выполнить две задачи на построение линии пересечения п

верхностей различными способами. Пример выполнения листа представлен на рис. 13.

о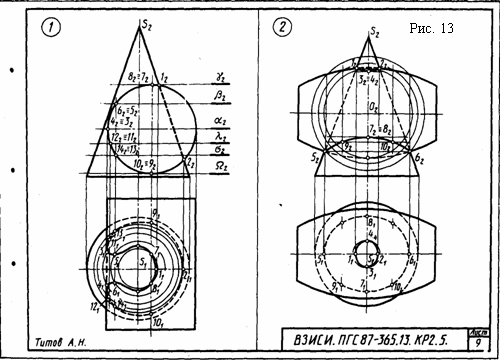

Задача 1. Дано: две пересекающиеся кривые поверхности. Требуется: способом вспомогательных секущих плоскостей построить линию их пересечения, выделив видимые и невидимые участки. Данные варианта задачи берут из табл. 11. Таблица 11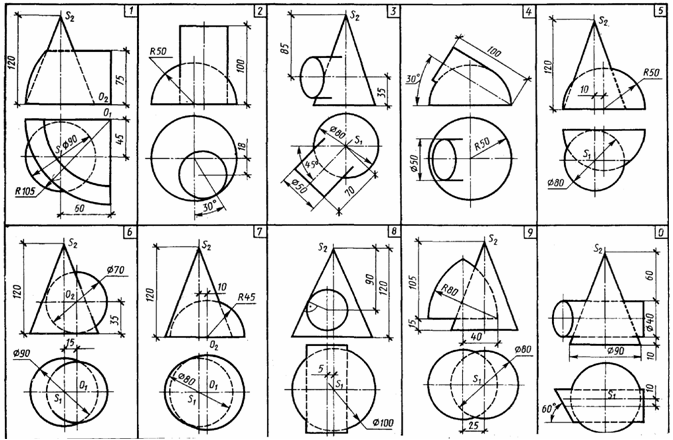



Указания к задаче 1. Задачу выполняют с левой стороны листа в такой последовательности: 1) определяют точки пересечения очерковых образующих одной поверхности с другой, а затем второй поверхности с первой; 2) определяют наивысшие и наинизшие точки линии; 3) определяют промежуточные точки линии пересечения; 4) все найденные точки пересечения последовательно соединяют кривой линией, учитывая видимость.

При выборе вспомогательных секущих плоскостей необходимо помнить, что они должны пересечь одновременно обе поверхности и дать наипростейшие фигуры сечения. Для всех вариантов заданий вспомогательно - секущими плоскостями могут быть выбраны плоскости уровня; для одних - горизонтальные, для других - вертикальные или те и другие. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательно - секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линии пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения самой секущей плоскости.

Задача 2. Дано: две пересекающиеся поверхности вращении. Требуется: способом секущих концентрических сфер построить линию их пересечения и определить ее видимость. Данные варианта задачи берут из табл. 12. Таблица 12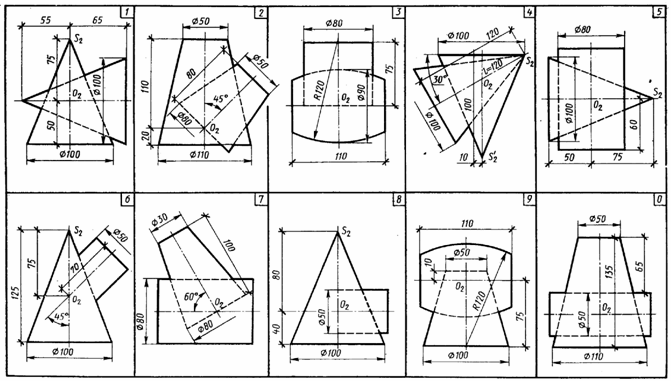



У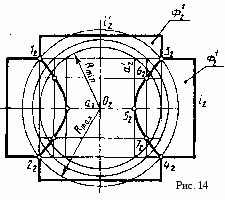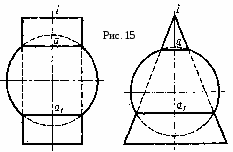казания к задаче 2. Задачу выполняют на правой половине листа в следующем порядке: 1) определяют центр концентрических сфер - точку пересечения осей поверхностей вращения - и проводят ряд концентрических окружностей - сфер различного радиуса. Диапазон радиусов сфер определяется минимальным и максимальным радиусами. Минимальный радиус секущей сферы назначается из условия касания сферы одной и пересечения другой пересекающейся поверхностей. Максимальным радиусом является отрезок прямой от центра сферы до наиболее удаленной точки пересечения очерков пересекающихся поверхностей (Ф¹ и Ф² на рис. 14); 2) строят линии пересечения выбранных сфер с заданными пересекающимися поверхностями. Каждая из сфер, будучи соосной с заданными поверхностями, пересечет их по окружностям, которые в данной задаче на плоскости П₂ представляют собой прямые линии - хорды окружности, называемые параллелями (рис. 15). Точки пересечения проекций полученных параллелей являются проекциями искомых точек линии пересечения поверхностей; 3) найденные точки пересечения поверхностей соединяют плавной кривой линией; 4)достраивают горизонтальную проекцию линии пересечения по имеющимся точкам.
Лист 10

Формат АЗ. Основная надпись по форме 4 б. Выполнить четыре задачи на построение аксонометрических проекций плоских и пространственных фигур. Пример исполнения листа приведен на рис. 16. Расположение элементов задач с их построением и обозначением выполнить в соответствии с примером. Разбивку поля чертежа для отдельных задач выдержать согласно размерам рис. 16, но линии границ не наносить.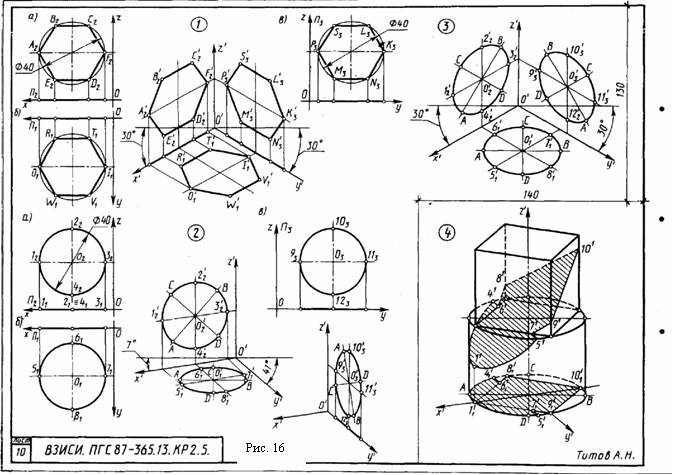



Задача 1. Дано: ортогональные проекции трех правильных шестиугольников, принадлежащих плоскостям проекций П₁, П₂, П₃ (рис. 16, задача 1, изображения а, б, в). Требуется: построить их аксонометрические проекции в прямоугольной изометрии. Описанные окружности для построения правильных шестиугольников имеют диаметр 40 мм.

У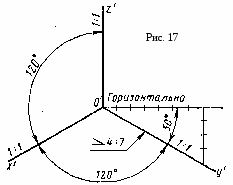казания к задаче 1. Задачу выполняют в такой последовательности: 1) строят проекции трех правильных шестиугольников, которые расположены в плоскостях проекций П₁, П₂, П₃ (рис. 16, задача 1, изображения а, б, в): 2) наносят оси координат, соответствующие прямоугольной изометрической проекции, и, используя приведенные коэффициенты искажения, намечают вершины шестиугольников по соответствующим аксонометрическим осям координат, которые затем соединяют линиями. При выполнении данной задачи следует помнить, что в прямоугольной изометрии угол между проецирующим лучом и плоскостью аксонометрических проекций равен 90°, аксонометрические оси координат располагают под углом 120° (рис. 17), действительные коэффициенты искажения по всем осям равны 0,82, но для практических построений применяют приведенные коэффициенты искажения, равные 1. При приведенных коэффициентах прямоугольная изометрия увеличивается а 1,22 раза (1 : 0,82 = 1,22), а прямоугольная диметрия - в 1,06 раза (1 : 0,94 = 1,06).

Задача 2. Дано: ортогональные проекции трех окружностей, соответственно принадлежащих плоскостям проекций П₁, П₂, П₃ (см. рис. 16, задача 2, изображения а, б, в). Требуется: построить их аксонометрические проекции в прямоугольной диметрии. Диаметр окружностей равен 40 мм.

Указания к задаче 2. Задачу выполняют в нижней левой части листа в следующем порядке: 1) строят ортогональные проекции окружностей и намечают на них характерные точки, соответственно расположенные в плоскостях проекций П₁, П₂, П₃ (см. рис. 16, задача 2, изображения а, б, в); 2) наносят акс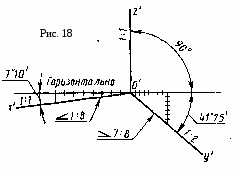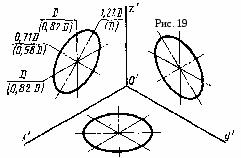онометрические оси координат, соответствующие прямоугольной диметрической проекции, и, используя приведенные коэффициенты искажения, строят выбранные характерные точки окружностей, а также большую ось эллипса АВ и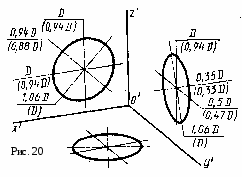 малую ось эллипса СD. Схема расположения осей и приведенные коэффициенты искажений изображены на рис. 17, 18. Тут же на схеме указаны уклоны аксонометрических осей для их построения. Окружности в аксонометрии проецируются в виде эллипсов, причем при использовании действительных коэффициентов искажения большая ось эллипса равна диаметру окружности (рис. 19, 20). Так как приведенные коэффициенты аксонометрического изображения увеличивают, то, следовательно, большая в малая оси тоже увеличиваются. В табл. 13 приведены значения осей эллипсов для различных положений окружностей и видов аксонометрий. При построении аксонометрической окружности нужно помнить, что во всех трех плоскостях прямоугольной изометрической и диметрической проекций большая ось эллипса должна быть направлена перпендикулярно оси, которая отсутствует в этой плоскости, а малая ось сохраняет направление отсутствующей этой плоскости оси. Таблица 13

Оси эллипса

Прямоугольная изометрия

Прямоугольная диметрия

К= 0,82

К= 1

К= 0,94

К= 1

x101y1

x101z1

y101z1

x101y1

x101z1

y101z1

x101y1

x101z1

y101z1

x101y1

x101z1

y101z1

Большая ось

D

D

D

1,22D

1,22D

1,22D

D

D

D

1,06D

1,06D

1,06D

Малая ось

0,58

0,58

0,58

0,71

0,71

0,71

0,33

0,88

0,33

0,35

0,94

0,35

Задача З. Дано: ортогональные проекции трех окружностей, соответственно принадлежащих плоскостям проекций П₁, П₂, П₃ (См. рис. 16, задача 2, изображения а, б, в). Требуется: построить их аксонометрические проекции в прямоугольной изометрии. Диаметр окружностей равен 40 мм.

Указания к задаче З. Для решения задачи используют ортогональные проекции окружностей, которые присутствуют в условии задачи 2 Листа 10. Последовательность выполнения задачи 3 полностью соответствует порядку решения задачи 2 этого же листа. Коэффициент искажения по оси указан на рис. 17, большие и малые оси в табл. 13, а их изображение приведено на рис. 19.

Задача 4. Дано: ортогональные проекции комбинированной поверхности и сечение этой поверхности фронтально - проецирующей плоскость. Требуется: построить прямоугольную изометрию или прямоугольную диметрию комбинированной поверхности вместе с контуром сечения этой поверхности плоскостью. За исходные данные для построения аксонометрии комбинированной поверхности берут ортогональные проекции задачи 3 листа 7 (см. рис. 11) и найденное на них сечение от фронтально - проецирующей плоскости. Вид аксонометрии студент определяет сам.

Указания к задаче 4. Задачу выполняют в нижней правой части листа в такой последовательности: 1) на ортогональном чертеже наносят оси прямоугольной системы координат, к которой относят заданную поверхность; 2) выбирают вид аксонометрии с таким расчетом, чтобы обеспечить наилучшую наглядность поверхности, и наносят аксонометрические оси координат; 3) в системе координат Х¹0¹У¹ строят вторичные проекции оснований поверхностей и сечения; 4) каждую точку вторичной проекции поднимают на высоту ее положения, которое она занимает в натуре, и по этим точкам строят аксонометрическое изображение.

В процессе выполнения любой аксонометрии следует запомнить, что выполнение аксонометрии нужно начинать со вторичной проекции, т. е. с построения аксонометрии плоской фигуры, являющейся видом данного предмета сверху или спереди. Поэтому для выполнения листа 10 первые три задачи были на построение плоских фигур.

Лист 11

Формат АЗ. Основная надпись по форме 4а. Выполнить четыре позиционные и метрические задачи в проекциях с числовыми отметками. Пример выполнения чертежа приведен на рис. 21.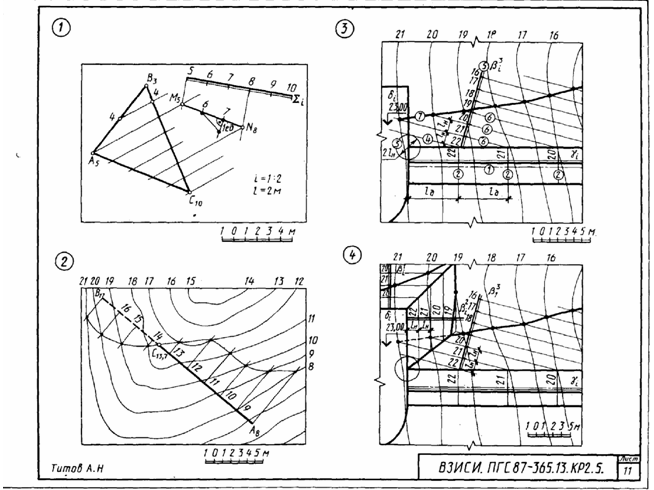



Рис. 21

Задача 1. Дано: плоскость, заданная треугольником  (А, В, С), и плоскость, заданная масштабом уклонов. Требуется: построить линию пересечения этих плоскостей и определить уклон и интервал линии пересечения плоскостей. Исходные данные студент задает сам в соответствии с условием задачи, не забывая приводить масштаб чертежа.

У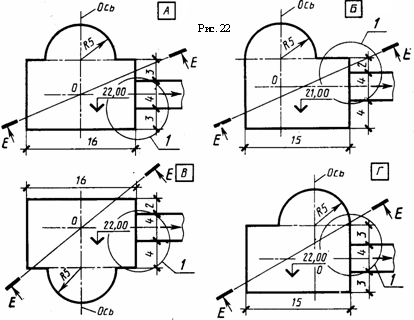казания к задаче 1. Задачу выполняют в верхней левой части листа в следующем порядке: 1) по описанию задачи задается графическое условие; 2) строят горизонтали заданных плоскостей: для треугольника АВС - посредством градуировання сторон, а для плоскости Σ направление горизонталей перпендикулярно масштабу уклонов (см. рис. 21); 3) отмечают точки пересечения двух одноименных пар горизонталей, обозначают и проставляют числовые отметки; 4) определяют интервал и уклон линии пересечения.

Интервал - величина заложения на единицу превышения прямой. Для его получения градуируют линию пересечения, по масштабу определяют величину интервала между соседними точками прямой, разность отметок которых равна единице.

Уклон - превышение прямой на единицу заложения, Поэтому на отрезке интервала строят прямоугольный треугольник, второй катет которого равен единице масштаба, Из соотношения катета противолежащего к прилежащему устанавливают уклон прямой линии пересечения. На рис. 21 (задача 1) установлено, что интервал равен 2 м, а уклон i = 1 : 2.

Задача 2. Дано: топографическая поверхность, заданная горизонталями, и прямая, заданная двумя точками отрезка. Требуется: построить точку пересечения прямой с топографической поверхностью и определить ее отметку. Графическое условие задачи студент задает самостоятельно исходя из ее описания.

Указания к задаче 2. Для решения задачи выполняют следующее: 1) по описанию задачи вычерчивают ее графическое условие и масштаб чертежа; 2) заданную прямую градуируют и через нее проводят плоскость общего положения, задав ее произвольными горизонталями; 3) определяют линию пересечения вспомогательной плоскости с заданной поверхностью через точки пересечения одноименных горизонталей; 4) отмечают точку пересечения проекции прямой с проекцией линии пересечения вспомогательной секущей плоскости с заданной поверхностью и устанавливают ее отметку как точки, лежащей на прямой.

З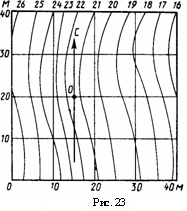адача 3. Для узла 1 (рис. 22) задать плоскость полотна дороги в проекциях с числовыми отметками и определить линию пересечения плоскостей откоса дороги рельефом местности. На изображение нанести мнемонические знаки, раскрывающие последовательность выполнения элементарных графических процедур.

Указания к задаче 3. Предварительно по своему варианту студент должен вычертить графическое условие для листа 12; план земельного участка с горизонталями и земляное сооружение на нем, используя для этого рис. 22, 23 и указания к листу 12. Затем построить масштабы уклонов с горизонталями для плоскостей и полотна дороги. Далее необходимо аккуратно перечертить на прозрачную бумагу и перенести на лист 11 фрагмент узла 1 (см. рис. 22) плана сооружения с дорогой и горизонталями в качестве исходных данных к заданной задаче.

Задача 4. Для узла 1 (см. рис. 22) построить линию пересечения плоскостей насыпи (выемки) сооружения и дороги, а также линии пересечения плоскостей насыпи (выемки) с рельефом местности.

Указания к задаче 4. Исходные графические данные аналогичны предыдущей задаче.
Лист 12

Формат АЗ. Основная надпись по форме 4б. Выполнить две задачи, связанные с определением границ земляных работ при строительстве земляного сооружения и профиля земляного сооружения. Пример выполнения листа см. на рис. 24.
Задача 1. Дано: топографическая поверхность, заданная горизонталями, и земляное сооружение с указанными уклонами откосов (см. рис. 22 и 23). Откосы выемок имеют уклон 1 : 1, откосы насыпей 1 : 1.5 и уклон дороги 1 : 6. Требуется; построить линии пересечения откосов выемок и насыпей земляного сооружения (площадки и дороги) между собой и с топографической поверхностью. Форму и размеры земляного сооружения (см. рис. 22) выбирают по данным варианта табл. 14.

Указания к задаче 1. Для выполнения задания необходимо проделать следующее: 1) начертить в масштабе 1 : 200 план земельного участка, рельеф которого задан горизонталями (см. рис. 23), и нанести на него в том же масштабе план земляного сооружения так, чтобы центр сооружения О совпал с центром участка О и ось сооружения была наклонена к меридиану под заданным углом. Горизонтали топографической поверхности обвести цветной тушью (лучше жженой сиеной) или цветной пастой шариковой ручки, что облегчает последующие построения карандашом, толщина линий обводки 0,1...0,2 мм. Контур земляного сооружения и линии пересечения откосов с топографической поверхностью и между собой обводят карандашом линиями толщиной 0,4...0,6 мм; штриховку откосов выемок и насыпей выполняют линиями толщиной 0,1. . .0,2 мм перпендикулярно проектным горизонталям при расстоянии между штрихами 1.5. .2.5 мм; линии построения (в том числе проектные горизонтали) должны иметь толщину 0,1...0.2 мм; 2) проанализировать и обозначить все плоскости и поверхности земляного сооружения при помощи масштабов уклонов, как это показано на рис. 24. Построить горизонтали всех откосов земляного сооружения и дороги с учетом заданных уклонов для них. Для построения горизонталей необходимо при помощи графика масштаба уклонов определить величину интервалов для откосов насыпей, выемок и дороги в масштабе чертежа (1 : 200), затем нанести эти интервалы на масштабах уклонов всех откосов и провести горизонтали перпендикулярно масштабам уклонов; 3) используя точки пересечения одноименных горизонталей, построить линию пересечения откосов между собой и с топографической поверхностью.

Задача 2. Дано: топографическая поверхность и земляное сооружение на ней. Требуется: построить профиль сооружения - сечение от вертикальной плоскости Е-Е. Задача выполняется по результатам решения задачи 1. Положение секущей плоскости указано на рис. 22. Пример выполнения задачи приведен на рис. 24.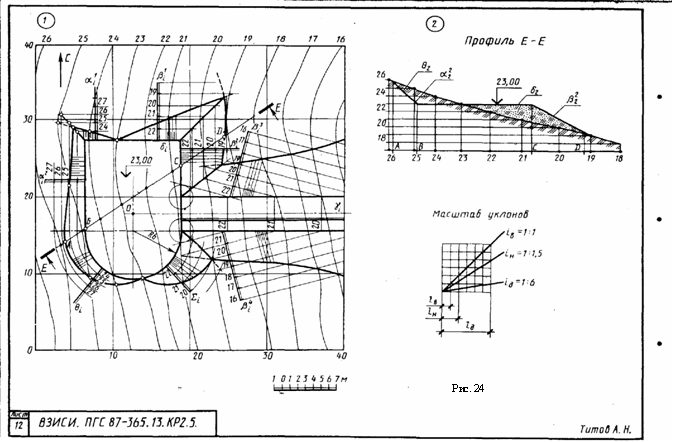



Указания к задаче 2. Задачу выполняют в такой последовательности: 1) в масштабе 1 : 200 на расстоянии 1 м по высоте изображают горизонтали рельефа в пределах отметок той части сооружения, которая пересекается плоскостью Е-Е; 2) строят профиль земли; для этого измеряют и откладывают на чертеже горизонталей точки пересечения горизонталей топографической поверхности и следа секущей плоскости. Из полученных точек восстанавливают вертикальные линии до горизонталей, отметки которых определяются отметками этих точек на топографической поверхности. Пересечения одноименных горизонталей и вертикальных линий соответствуют точкам профиля земли, соединяя которые плавной линией получают искомый профиль; 3) строят профиль земляного сооружения аналогично построению профиля земли. При выполнении листа 12 следует помнить следующие положения:.

1. Точка в проекциях с числовыми отметками задается своей горизонтальной проекцией и числом при ней (отметкой), выражающим высоту этой точки над горизонтальной плоскостью, принятой за нулевую.

2. Прямая линия задается проекциями двух точек и их отметками или отметкой одной точки и уклоном. Во втором случае должно быть указано направление, в котором прямая опускается (стрелкой).

3. Плоскость может быть задана проекциями трех точек, не лежащих на одной прямой, и их отметками, двумя параллельными или пересекающимися прямыми (прямые задаются в соответствии с п. 2), точкой и непроходящей через нее прямой (см. п. 1 и 2). Кроме того, ее можно задать масштабом уклонов (градуированной линией наибольшего ската плоскости) или одной горизонталью и уклоном. В последнем случае указывают направление спуска плоскости.

4. Если прямые параллельны, то параллельны их проекции, одинаковы уклоны и их направления.

5. Линия пересечения плоскостей определяется точками пересечения двух пар однозначных горизонталей этих плоскостей.

6. Линия пересечения плоскости и поверхности или двух поверхностей определяется точками пересечения однозначных горизонталей обеих поверхностей (или плоскости и поверхности).

7. Для построения линии пересечения прямой с плоскостью или поверхностью нужно через прямую провести плоскость общего положения, задав ее произвольно выбранными горизонталями. Определив линию пересечения вспомогательной плоскости с заданной плоскостью или поверхностью, отмечают на ней точку, в которой эта линия пересекается с заданной прямой.

8. Так как топографическая поверхность в проекциях с числовыми отметками изображается большей частью с помощью горизонталей, то линию пересечения поверхности земляного сооружения (откосов) с топографической поверхностью можно построить, соединив точки пересечения однозначных горизонталей откосов и поверхности земли (см. п. 6).
ВОПРОСЫ ДЛЯ КОНТРОЛЯ ЗНАНИЯ
Ко всем ответам на вопросы необходимо привести соответствующие чертежи (эпюры). К ответам, номера вопросов которых отмечены надстрочной звездочкой, необходимо построить алгоритмы в блок- схемной форме и чертежи (эпюры) с использованием мнемонических знаков, указывающих последовательность выполнения элементарных графических процедур, и отметить минимальное число этих процедур.

К т е м е 1. Введение. Центральные и параллельные проекции. 1. Какое изображение называют рисунком? чертежом? 2. Какие основные методы проецирования геометрических форм на плоскости Вам известны? 3. Какие виды параллельных проекций Вы знаете? 4. Перечислите основные свойства параллельных проекций. 5. Перечислите основные требования, предъявляемые к проекционному чертежу. 6. Что называют обратимостью чертежа? 7. Сформулируйте и покажите на чертежах особенности ортогональных и аксонометрических проекций и проекций с числовыми отметками.

К т е м е 2. Точка, прямая, плоскость в ортогональных проекциях. 1. Что называют ортогональной проекцией точки? 2. Каких образом пространственная фигура из трех взаимно перпендикулярных плоскостей преобразуется в плоскую модель? 3. Как образуются проекции точки на плоскостях П₁, П₂, П₃? 4. Что называют координатами точки пространства в декартовой системе координат и какие координаты на эпюре определяют ее горизонтальную, фронтальную проекции? 5. Какую прямую называют прямой общего положения? 6. Перечислите прямые частного положения, дайте определение каждой из них и укажите особенности их проекций. 7. Что называют следом прямой? 8. Как построить горизонтальный и профильный следы прямой? 9. Как задаются на комплексном чертеже параллельные, пересекающиеся и скрещивающиеся прямые? 10. Как найти натуральную величину отрезка прямой методом прямоугольного треугольника? Как определить углы наклона отрезка прямой к плоскостям проекций П₁ и П₂? 11. В каком случае прямой угол проецируется в виде прямого? 12. Перечислите и изобразите графические способы задания плоскости на комплексном чертеже. 13. Что понимают под следом плоскости? 14. Какую плоскость называют проецирующей и каковы ее графические признаки на чертеже? 15. Дайте графические и физические характеристики плоскостям: горизонтально - проецирующей, фронтально - проецирующей, профильно-проецирующей? 16. Какую плоскость называют плоскостью уровня? 17. Какую плоскость называют горизонтальной? фронтальной? профильной? Изобразите их на эпюре.

К т е м е 3. Позиционные и метрические задачи. 1. Когда прямая принадлежит плоскости? 2. Когда точка принадлежит плоскости? 3. Перечислите и изобразите главные линии плоскости. 4. При помощи каких главных линий плоскости можно определять углы наклона плоскости к плоскостям проекций? 5. В каком случае прямая параллельна плоскости? 6. Как по чертежу установить параллельность прямой и плоскости? двух плоскостей? 7. В каком случае точка пересечения прямой с плоскостью видна непосредственно на заданном чертеже? 8. Покажите на чертеже, как можно прямую заключить в плоскость. 9. Перечислите этапы построения точки пересечения прямой с плоскостью общего положения 10. Сформулируйте теорему о перпендикуляре к плоскости. 11. В каком случае одна из проекций линии пересечения двух плоскостей непосредственно присутствует на заданном чертеже? 12. Изложите общий случай построения линии пересечения двух плоскостей. 13. Сформулируйте условие перпендикулярности двух плоскостей.

К те м е 4. Способы преобразования проекций. 1. В чем сущность преобразования проекций способом замены плоскостей проекций? 2. Назовите задачи, для решения которых достаточно заменить только одну плоскость проекций. 3. Назовите задачи, которые решаются заменой двух плоскостей проекций. 4. В чем сущность преобразования проекций способом вращения вокруг оси, перпендикулярной плоскости? 5. Назовите пять элементов вращения точки вокруг оси. 6. Чем отличается способ плоскопараллельного перемещения от способа вращения вокруг оси, перпендикулярной плоскости проекций? 7. Перечислите задачи, которые выполняют одним вращением и двумя.

К т е м е 5. Многогранники. 1. Какие поверхности называют многогранниками? 2. Какие многогранники называют правильными? 3. Какими элементами задаются многогранники на чертеже? 4. Изложите построения сечения многогранника плоскостью: а) частного положения, б) общего положения. 5. Изложите алгоритм построения точек пересечения прямой линии с многогранником 6. Изложите сущность двух способов построения линии взаимного пересечения многогранников. 7. Как доказать, что точка лежит на поверхности многогранника?

К т е м а м 6 и 7. Кривые линии. Поверхности. 1. Какие кривые линии называют алгебраическими и какие - трансцендентными? 2. Какие точки кривой относят к характерным? 3. Что называют порядком алгебраической кривой? 4. Что называют кривизной плоской кривой и как ее определяют графически? 5. Какие пространственные кривые называют гелисами и как их задают на чертеже? 6. Укажите основные способы задания поверхностей. 7. Что называют каркасом поверхности? 8. Что называют определителем поверхности? 9. Как образуются и задаются на чертеже поверхности переноса прямолинейного направления, поверхности вращения, винтовые поверхности? 10. Укажите основные свойства поверхностей вращения. 11. Какие винтовые поверхности называют геликоидами? Укажите их виды. 12. Какие кривые поверхности называют линейчатыми поверхностями с направляющей плоскостью? 13. Какую поверхность называют цилиндроидом? коноидом? Как они задаются на чертеже? 14. Назовите поверхности вращения с прямолинейной образующей. 15. Назовите наиболее распространенные поверхности вращения с криволинейной образующей. 16. Назовите линейчатые развертывающиеся поверхности. 17. Как построить точку и линию принадлежавшие поверхности?

К т е м е 8. Пересечение поверхностей плоскостью и прямой линией. 1. Укажите общую схему определения точек линии пересечения поверхности проецирующими плоскостями. 2. Укажите общую схему определения точек линии пересечения поверхности плоскостью общего положения. 3. Какие точки линии пересечения поверхности плоскостью называют опорными (характерными)? 4. Укажите условия, про которых в сечении конуса вращения плоскостью получаются окружность, эллипс, гипербола, парабола, пересекающиеся прямые, точка. 5. Как построить высшую и низшую точки конического сечения?

К т е м е 9. Взаимное пересечение поверхностей. 1. Объясните на графическом примере общую схему построения линий пересечения поверхностей. 2. Назовите основные способы построения линий пересечения поверхностей. 3* Опишите способы секущих плоскостей и сферических посредников при определении линии пересечения поверхностей. 4. Изложите общие принципы выбора вспомогательно - секущих плоскостей и сфер при построении линии пересечения поверхностей 5. В каком случае поверхности вращения пересекаются по окружностям? 6. Какое пересечение поверхностей называют полным и неполным? 7. В какой последовательности соединяются точки искомой линии пересечения поверхностей и как определяется видимость линии? 8*. Изобразите общую схему построения точек пересечения прямой с поверхностью. 9. Укажите, какие могут быть случаи пересечения прямой с поверхностью.

К т е м е 10. Плоскости, касательные к поверхности. 1. Какую плоскость называют касательной к поверхности в данной точке? 2. Что называют нормалью поверхности в данной точке?

К т е м е 11. Развертки поверхностей. 1. Что называют разверткой поверхностей? 2. Какие поверхности называют развертывающимися и какие неразвертывающимися? 3. Укажите основные свойства разверток. 4. Укажите последовательность графических построений разверток поверхностей конуса и цилиндра. 5. Что называют аппроксимацией поверхности? б. Какие способы разверток многогранников Вы знаете?

К т е м е 12. Аксонометрия. 1. Какие проекции называют аксонометрическими? 2. Назовите виды аксонометрических проекций. 3. Что называют коэффициентом искажения? 4. Сформулируйте основную теорему аксонометрии - теорему Польке. 5. Назовите коэффициенты искажений по направлениям осей в прямоугольной изометрии и диметрии. б. Укажите направления и величины осей эллипсов как изометрических и диметрических проекций окружностей при условии использования проведенных коэффициентов искажения.

К т е м е 13. Проекции с числовыми отметками. Точка. Прямая. Плоскость. 1. В чем сущность метода проекций с числовыми отметками? 2*. Что называют уклоном и интервалом прямой? 3* Что такое градирование прямой? 4*, Что понимают под масштабом уклона плоскости? 5. Как расположены горизонтали плоскости к масштабу уклонов? 6. Какой угол называют углом падения плоскости? 7. Какой угол называют углом простирания 8*. Как строится линия пересечения двух плоскостей в проекциях с числовыми отметками? 9* Как определить точку пересечения прямой с плоскостью?

К т е м е 14. Проекции с числовыми отметками. Поверхности. 1. Изобразите на чертеже коническую, цилиндрическую и топографическую поверхности. 2. Что понимают под горизонталями поверхности? 3* Приведите схему построения точек пересечений прямой с поверхностью. 4*, Как строится линия пересечения плоскости с топографической поверхностью? 5*, Объясните построение горизонталей поверхностей одинакового ската. 6. Какое изображение называют профилем топографической поверхности? 7*, Приведите пример построения профиля.
ЗАДАЧИ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

К задачам, номер которых отмечены надстрочной звездочкой, необходимо построить алгоритмы в блок-схемной форме и чертежи (эпюры) с использованием мнемонических знаков, указывающих последовательность выполнения элементарных графических процедур, и отметить минимальное число этих процедур.

Задачи (см. текст и чертежи к ним) предназначены для самостоятельного решения студентами в процессе изучения ими курса перед выполнением контрольных работ и для подготовки к экзаменам.

Все построения выполняются карандашом с применением чертежных инструментов. Линии построения, необходимые для решения каждой задачи, следует сохранить на чертеже. Допускается применение цветных карандашей. В задачах, в которых есть текстовое условие, но нет графического сопровождения, чертеж выполнить самостоятельно (придумать). Заданное графическое условие увеличивайте в 1,5. . .2 раза для лучшего понимания чертежей обозначайте характерные точки. Решать задачи легче я тетради в клеточку.

К т е м а м 2 и 3. Точка, прямая, плоскость, позиционные и метрические задачи.

1. Построить проекции точек А, В и С по координатам: А (2, 1, 3), В (3, 3, 4), С (5, 4, 2). Первой дана координата Х, второй - У, третьей - Z. Таблица I



2*. Определить длину отрезка прямой а(А, В) и построить фронтальный и горизонтальный следы прямой а (А. В).

3. Построить фронтальный и горизонтальный следы плоскости , заданной точками А, В и С, не лежащими на одной прямой.

4. Построить горизонтальную проекцию треугольника АВС, принадлежащего плоскости , и определить углы и наклона плоскости  соответственно к плоскостям проекций П₁ и П₂.

5* Определить точку пересечения прямой а с плоскостью  (А, В, С) (А, В, С).

6. Построить линию пересечения плоскости  (А, В, С) с плоскостью β (а II b).

7* Через точку А провести плоскость, параллельную плоскости β (а II b), задав ее пересекающимися прямыми.

8*. Определить расстояние от точки А до плоскости  (А, В, С) (без преобразования проекций).

9. Провести через точку С плоскость , перпендикулярную прямой а. Задать плоскость пересекающимися прямыми.

К т е м е 4. Способы преобразования проекций.

10. Способом вращения вокруг осей, перпендикулярных плоскостям проекций, определить величину треугольника АВС.

11. Способом замены плоскостей проекций определить расстояние между параллельными плоскостями  и β.

12. Способом совмещения плоскости с одной из плоскостей проекций построить проекции равностороннего треугольника АВС,. принадлежащего плоскости , по его стороне АВ.

стороне АВ.

13*. Способом плоскопараллельного перемещения определить расстояние от точки С до прямой а (А, В).

14* Способом замены плоскостей проекций определить расстояние от точки А до плоскости  (А, В, С).

15. Повернуть точку К вокруг оси i до совмещения с плоскостью  (А, В, С).

К т е м е 5. Многогранники.

16, 17, 8, 19. Построить линию пересечения поверхности плоскостью.

20, 21. Построить точки пересечения прямой с многогранником.

К т е м е 6. Кривые линии.

22. Достроить фронтальную проекцию плоской кривой линии, принадлежащей плоскости  (А, В, С). Таблица II



23. Построить винтовую линию, расположенную на боковой поверхности цилиндра, у которого диаметр 30 мм, а высота - 60 мм.

К т е м е 7. Поверхности.

24. Постройте две проекции произвольного коноида, если его одна направляющая горизонтальная линия, вторая - произвольная кривая.

25. Постройте две проекции произвольного прямого винтового геликоида.

26. Постройте три проекции сферы с вертикальным трехгранным отверстием, расположенным произвольно.

27. Построить три проекции прямого кругового конуса с произвольным горизонтальным цилиндрическим отверстием.

К т е м е 8. Пересечение поверхности плоскостью и прямой.

28’. Построить проекции линии пересечения поверхности конуса с плоскостями  и β, найти натуральную величину сечений. Назвать, какая линия ограничивает каждое сечение,

29. Построить линию пересечения сферы и плоскости . Определить натуральную величину сечения.

30* Построить точки пересечения прямой а с поверхностью цилиндра

31* Построить, точки пересечения прямой а с поверхностью конуса.

32* Построить, точки пересечения прямой а с полусферой. Таблица III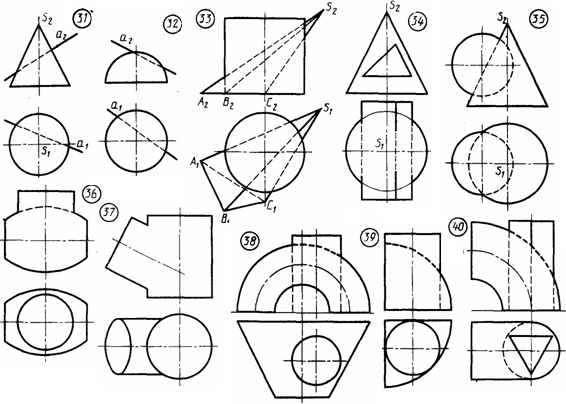



К 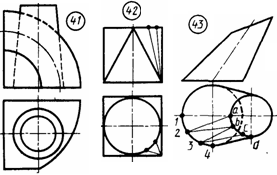т е м е 9. Взаимное пересечение поверхностей.

33. Построить линию пересечения поверхностей пирамиды АВСS и прямого кругового цилиндра.

34. Построить линию пересечения поверхностей конуса и призмы.

35. Построить линию пересечения сферы к поверхности конуса.

36. Используя способ вспомогательных секущих сфер, построить линию пересечения поверхностей двух цилиндров.

37. Используя способ вспомогательных секущих сфер, построить линию пересечения тора и поверхности цилиндра.

38. Построить линию пересечения усеченной половины конуса с прямым цилиндром.

39. Построить линию пересечения четверти сферы с цилиндром.

40. Построить линию пересечения четверти тора с вертикальной призмой.

41. Построить линию пересечения усеченной четверти сферы с усеченным конусом.

К т е м е 10. Развертки поверхностей.

42. Выполнить развертку перехода от квадрата к кругу.

43. Выполнить развертку перехода от круга одного диаметра к кругу другого. Диаметры кругов разные и расположены в непараллельных плоскостях.

К т е м е 12. Аксонометрия.

44. Построить прямоугольную диметрию куба, длина ребра которого равна 30 мм. Три ребра куба лежат соответственно на осях Х, У и Z.

45. Построить прямоугольную изометрию цилиндра, диаметр основания которого равен 30 мм, а высота - 40 мм. Центр нижнего основания цилиндра расположен в точке А, а ось вертикальна.

К т е м е 13. Проекции с числовыми отметками. Точка. Прямая. Плоскость.

46. Определить расстояние между прямыми а (В, Е) и b (А, D), если известны их уклоны и отметки точек В и А.

47. Определить угол наклона и интервал прямой а(А₄, В₇), если заложение этой прямой равно 9 единицам.

48. Построить точку пересечения прямой а(А₇, В₂) с плоскостью, заданной горизонталью «3» и уклоном 2:1.

49. В плоскости (А₂, В₈, С₃) провести прямую с уклоном 1: 5.

К т е м е 15. Тени в ортогональных и аксонометрических проекциях.

50. Построить тень, падающую от треугольника АВС на плоскости проекций, и тень, падающую от отрезка прямой а(А, Е) на плоскость треугольника.

51. Построить тень, падающую на плоскость II₂ от окружности и описанного вокруг нее квадрата и его диагоналей.

52. Построить собственные и падающие тени призмы и падающую тень треугольника АВС в ортогональных проекциях и аксонометрии. При построении тени от прямой а (А, В) на поверхность призмы следует воспользоваться способом обратного луча.

53. Построить собственную тень полуцилиндра и падающие тени от карниза на полуцилиндр и стену, а также от полуцилиндра на стену. Таблица IV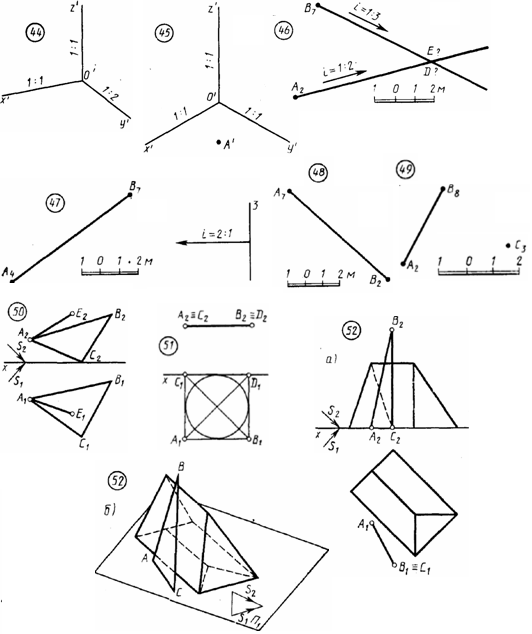



Таюлица V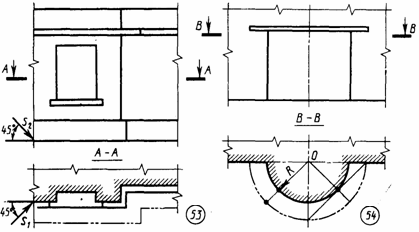




МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ЧЕРЧЕНИЯ

Задача курса состоит в том, чтобы научить студентов правильно читать и выполнять строительные и машиностроительные чертежи. Все чертежи выполняют в соответствии с государственными стандартами СПДС и ЕСКД. При изучении курса черчения студентами целесообразно придерживаться такой последовательности: ознакомиться с очередной темой рабочей программы и рабочим планом изучения черчения, приведенным на с. 14, изучить стандарты и рекомендуемую литературу по данной теме; законспектировать в рабочую тетрадь основные положения темы и зарисовать по ним отдельные чертежи; выполнить графическую работу по теме в порядке указанном в методических указаниях.