КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех. Методические указания и контрольные задания для студентовзаочников технических специальностей высших учебных заведений
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
|
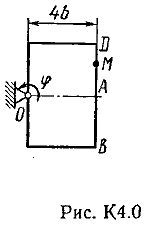
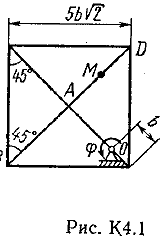
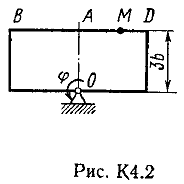
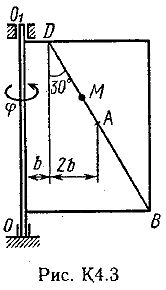
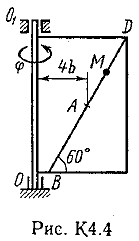
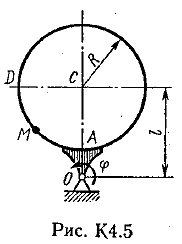
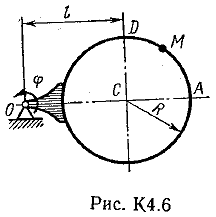
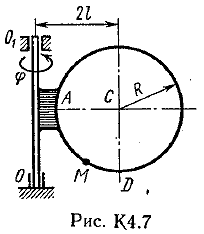
Ответ: υB=0,46 м/с; υE=0,46 м/с; ώ2=0,67 с-1; аB=0,72 м/с2; έ3=2,56 с-2. Задача К4 Прямоугольная пластина (рис. К 4.0К 4.4) или круглая пластина радиуса R=60 см (рис. К 4.5К 4.9) вращается вокруг неподвижной оси по закону =f1(t) заданному в табл. К 4. Положительное направление отсчета угла показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения ОО1лежит в плоскости пластины (пластина вращается в пространстве). По пластине вдоль прямой BD(рис. 04) или по окружности радиуса R(рис. 59) движется точка М; закон ее относительного движения, т. е. зависимость s=AM=f2(t)(sв сантиметрах, tв секундах), задан в таблице отдельно для рис. 0-4 и для рис. 5-9; там же даны размеры bи l. На рисунках точка М показана в положении, при котором s=AM>0 (при s<0 точка М находится по другую сторону от точки А). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1=1с. 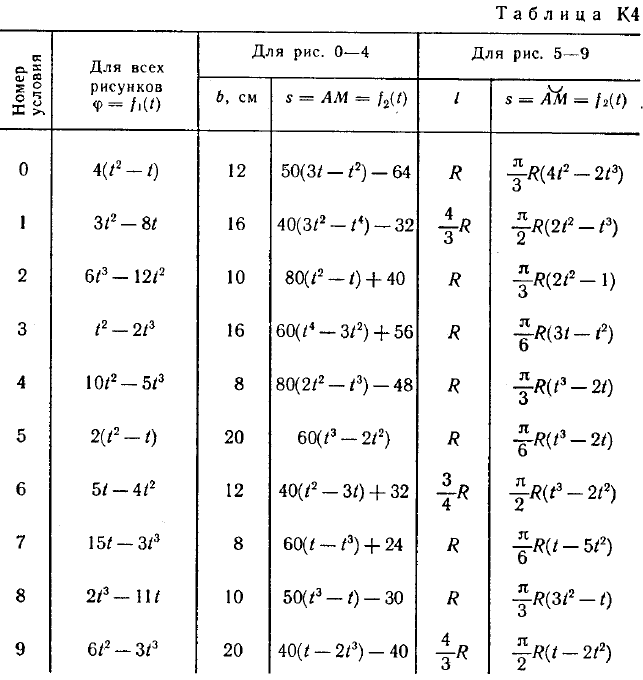
Пример К4а. Дано: R=0,5 м, =t2–0,5t3, s=πRcos(πt/3) ( – в радианах, s – в метрах, t – в секундах). 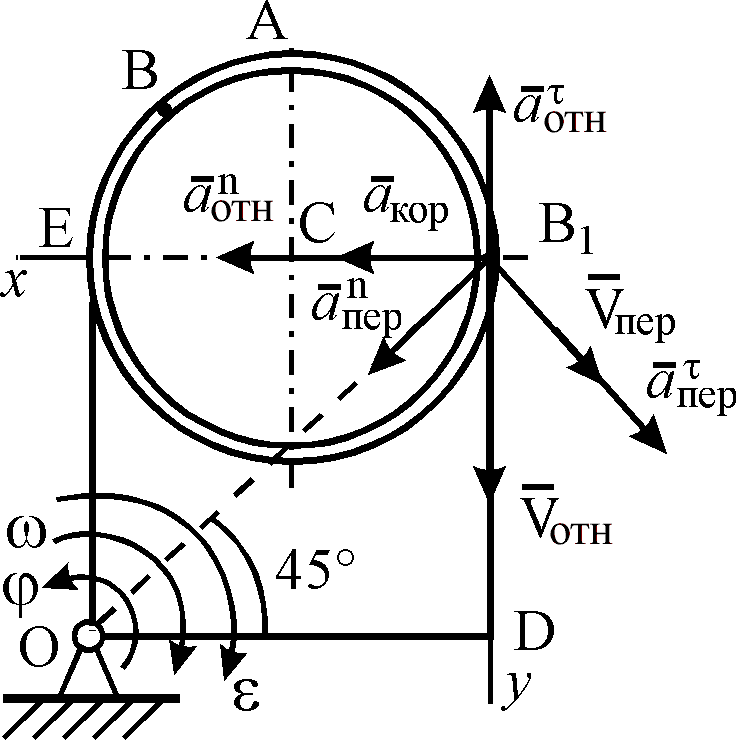 Определить: Vабс и аабс в момент времени t1=2 с. Решение. Рассмотрим движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины переносным движением. Тогда абсолютная скорость Vабс и абсолютное ускорение аабс точки найдутся по формулам: 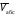 = = 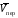 + + 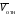 , , 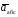 = = 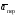 + + 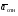 + + 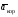 , ,где, в свою очередь, 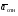 = = 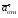 + + 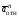 , , 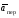 = = 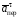 + + 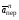 . . Рис. К4а Определим все, входящие в равенства, величины. Рассмотрим каждое движение в отдельности. 1. Относительное движение (мысленно остановить вращение пластины вокруг опоры О). Это движение происходит по закону 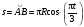 . .Положение точки В на дуге окружности в момент времени t1=2 с: 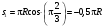 . .Знак минус свидетельствует о том, что точка В в момент t1=2 с находится справа от точки А. Изображаем ее на рис. К4а в этом положении (точка B1). Тогда 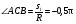 . .Теперь находим числовые значения Vотн, аотн, аnотн: 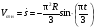 ; ;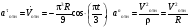 , ,где ρ – радиус кривизны относительной траектории, равный радиусу окружности R. Для момента t1=2 с, учитывая, что R=0,5 м, получим: 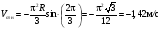 ; ;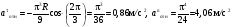 . .Знаки показывают, что вектор аотн направлен в сторону положительного отсчета расстояния s, а вектор Vотн-в противоположную сторону; вектор аnотн направлен к центру С окружности. Изображаем все эти векторы на рис. К4а. 2. Переносное движение (мысленно остановить движение точки по окружности). Это движение (вращение) происходит по закону =t2 – 0,5t3. Найдем угловую скорость и угловое ускорение ε переносного вращения при t1=2 с: 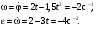 Знаки указывают, что в момент t1=2 с направления и ε противоположны направлению положительного отсчета угла ; отметим это на рис. К4а. Для определения Vпер и апер находим сначала расстояние h1=ОВ1точки B1 от оси вращения О. Из рисунка видно, что 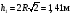 . Тогда в момент времени t1=2 с получим: . Тогда в момент времени t1=2 с получим: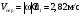 ; ;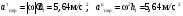 . .Изображаем на рис. К4а векторы Vпер и aперс учетом направлений и ε и вектор аnпер (направлен к оси вращения). 3. Ускорение Кориолиса. Модуль ускорения Кориолиса определяем по формуле: 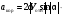 , ,где – угол между вектором Vотн и осью вращения (вектором ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор Vотн. Тогда в момент времени t1=2 с, учитывая, что в этот момент |Vотн|=1,42 м/с и ||=2 с-1, получим акор=5,68 м/с2. Направление акорнайдем по правилу Н. Е. Жуковского: так как вектор υотнлежит в плоскости, перпендикулярной оси вращения, то повернем его на 900 в направлении ώ, т. е. по ходу часовой стрелки. Изображаем акор на рис. К4а. [Иначе направление акор можно найти, учтя, что акор=2(ώ*υотн)]. Таким образом, значения всех входящих в правые части равенств (1) векторов найдены и для определения υабс и аабс остается только сложить эти векторы. Произведем это сложение аналитически. 4. Определение υа6с. Проведем координатные оси B1xy(см. рис. К4а) и спроектируем почленно обе части равенства υабс=υотн+υпер на эти оси. Получим для момента времени t1=2 с; 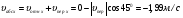 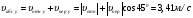 После этого находим 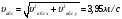 Учитывая, что в данном случае угол между υотн и υпер равен 45°, значение υабс можно еще определить по формуле 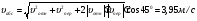 5. Определение аабс. По теореме о сложении ускорений 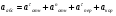 Для определения аабс спроектируем обе части равенства (7) на проведенные оси B1xy. Получим 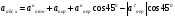 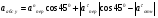 Подставив сюда значения, которые все величины имеют в момент времени t1=2 с, найдем, что в этот момент аабсх=9,74 м/с2; аавсу=7,15 м/с2 Тогда 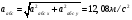 Ответ: υа6с=3,95 м/с, аабс=12,08 м/с2. Пример К4б. Треугольная пластина ADE вращается вокруг оси zпо закону = f1(t) (положительное направление отсчета угла показано на рис. К4б дуговой стрелкой). По гипотенузе AD движется точка Впо закону s = АВ = f2(t); положительное направление отсчета s – от А к D. 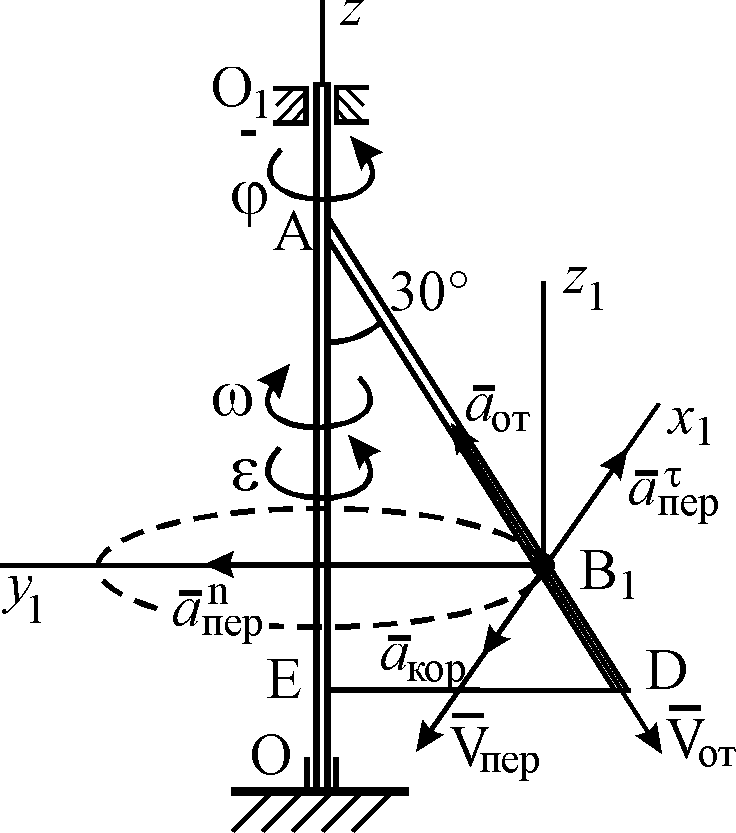 Дано: = 0,1 t3–2,2 t, s = АВ = 2 + 15 t – 3t2; ( – в радианах, s – в сантиметрах, t – в секундах). Определить: Vабс и аабс в момент времени t1 = 2 с. Рис. К4б Решение. Рассмотрим движение точки В, как сложное, считая ее движение по прямой AD относительным, а вращение пластины – переносным. Тогда абсолютная скорость 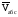 и абсолютное ускорение и абсолютное ускорение 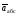 найдутся по формулам: найдутся по формулам: 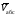 = = 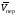 + + 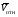 , , 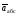 = = 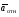 + + 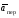 + + 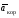 , ,где, в свою очередь, 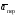 = = 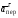 + + 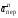 . .Определим все входящие в равенство величины. 1. Относительное движение это движение прямолинейное и происходит по закону s = AB = 2 + 15t 3t2, поэтому 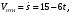 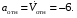 В момент времени t1 = 2 с имеем s1 = AB1 = 20 cм, Vотн = 3 см/с, аотн = 6 см/с2 Знаки показывают, что вектор 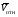 направлен в сторону положительного отсчета расстояния s, а вектор направлен в сторону положительного отсчета расстояния s, а вектор 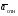 – в противоположную сторону. Изображаем эти векторы на рис. К4б. – в противоположную сторону. Изображаем эти векторы на рис. К4б.2. Переносное движение. Это движение (вращение) происходит по закону = 0,1t3 2,2t. Найдем угловую скорость и угловое ускорение переносного вращения: = 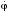 = 0,3t2 2,2; = = 0,3t2 2,2; =  = 0,6t и при t1 = 2 с, = 0,6t и при t1 = 2 с, = 1 c1, = 1,2 c2. Знаки указывают, что в момент t1 = 2 с направление совпадает с направлением положительного отсчета угла , а направление ему противоположно; отметим это на рис. К3б соответствующими дуговыми стрелками. Из рисунка находим расстояние h1 точки В1 от оси вращения z: h1 = AB1 sin 30° = 10 см. Тогда в момент t1 = 2 с, учитывая равенства (68), получаем: Vпер = ||h1 = 10 cм/с, 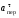 = ||h1 = 12 см/с2, = ||h1 = 12 см/с2, 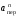 = 2h1 = 10 см/с2. = 2h1 = 10 см/с2.Изобразим на рис. К4б векторы 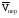 и и 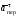 (с учетом знаков и )и (с учетом знаков и )и 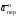 ; направлены векторы ; направлены векторы 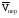 и и 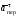 перпендикулярно плоскости ADE, а вектор перпендикулярно плоскости ADE, а вектор 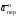 – по линии В1С к оси вращения. – по линии В1С к оси вращения.3. Кориолисово ускорение. Так как угол между вектором 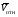 и осью вращения (вектором и осью вращения (вектором 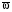 ) равен 30°, то численно в момент времени t1 = 2с ) равен 30°, то численно в момент времени t1 = 2с акор = 2|Vотн| || sin 30° = 3 см/с2. Направление 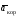 найдем по правилу Н. Е. Жуковского. Для этого вектор найдем по правилу Н. Е. Жуковского. Для этого вектор 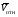 спроецируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору спроецируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору 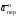 ) и затем эту проекцию повернем на 90° в сторону , т. е. по ходу часовой стрелки; получим направление вектора ) и затем эту проекцию повернем на 90° в сторону , т. е. по ходу часовой стрелки; получим направление вектора 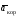 . Он направлен перпендикулярно плоскости пластины так же, как вектор . Он направлен перпендикулярно плоскости пластины так же, как вектор 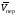 (см. рис. К3б). (см. рис. К3б).4. Определение Vабс. Так как 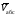 = = 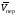 + + 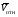 , а векторы , а векторы 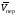 и и 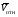 взаимно перпендикулярны, то взаимно перпендикулярны, то 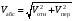 ; в момент времени t1 = 2 с Vабс = 10,44 см/с. ; в момент времени t1 = 2 с Vабс = 10,44 см/с.5. Определение аабс. По теореме о сложении ускорений 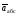 = = 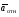 + + 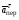 + + 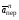 + + 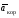 . .Для определения аабс проведем координатные оси В1хуz1 и вычислим проекции 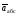 на эти оси. Учтем при этом, что векторы на эти оси. Учтем при этом, что векторы 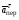 и и 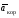 лежат на оси х1, а векторы лежат на оси х1, а векторы 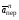 и и 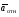 расположены в плоскости В1хуz1, т. е. в плоскости пластины. Тогда, проецируя обе части равенства (71) на оси В1хуz1 и учтя одновременно равенства (67), (69), (70), получаем для момента времени t1 = 2 с: расположены в плоскости В1хуz1, т. е. в плоскости пластины. Тогда, проецируя обе части равенства (71) на оси В1хуz1 и учтя одновременно равенства (67), (69), (70), получаем для момента времени t1 = 2 с:аабс х = | 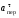 | – акор = 9 см/с2, | – акор = 9 см/с2,аабс у = 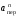 + |аотн|sin 30 ° = 13 см/с2, + |аотн|sin 30 ° = 13 см/с2,аабс z = |аотн|cos 30 ° = 5,20 см/с2. Отсюда находим значение аабс: 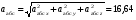 см/с2. см/с2.Ответ: Vабс = 10,44 см/с, аабс = 16,64 см/с2. Задача Д1. Груз D массой m, получив в точке А начальную скорость V0.движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 —Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления cреды R. зависящая от скорости V груза (направлена против движения); трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ=l или время t движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. х = x(t). где х = ВD. |