КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех. Методические указания и контрольные задания для студентовзаочников технических специальностей высших учебных заведений
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
|
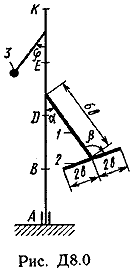
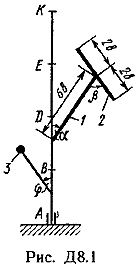
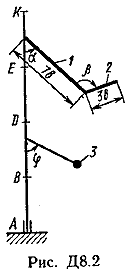
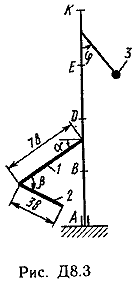
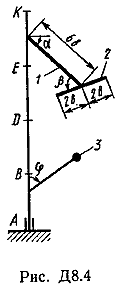
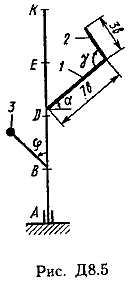
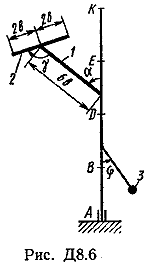
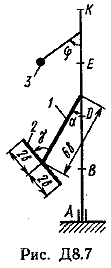
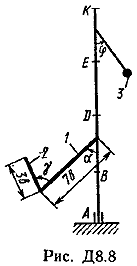
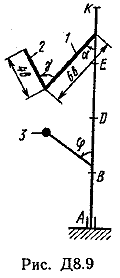
Ответ: ώ3=8,1 с-1. Задача Д8. Вертикальный вал АК (рис. Д8.0-Д8.9), вращающийся с постоянной угловой скоростью ώ=10 с-1 , закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ=BD=DE=ЕК=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой т=10 кг, состоящий из частей 1и 2(размеры частей стержня показаны на рисунках, где b=0,1 м, а их массы m1и m2 пропорциональны длинам), и невесомый стержень длиной l=4bсточечной массой т3=3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы , β, γ, даны в столбцах 5-8. Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а=0,6 м. 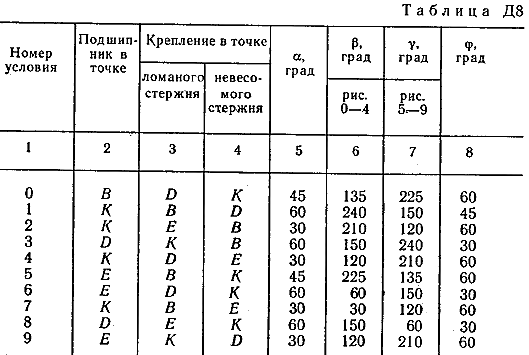
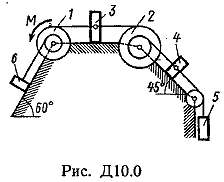
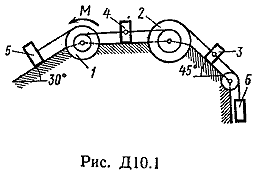
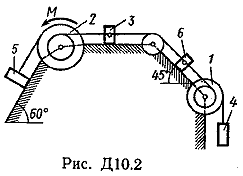
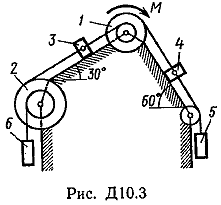
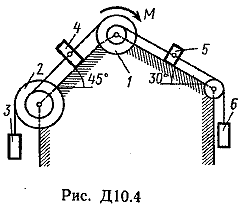
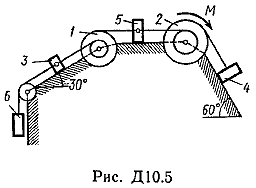
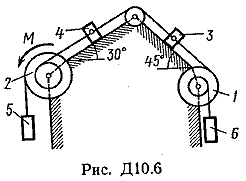
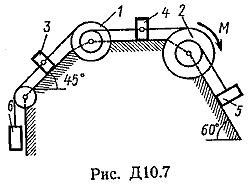
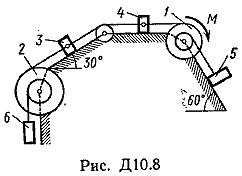
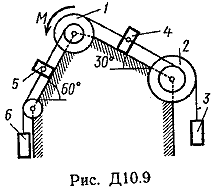
Пример Д8. Вертикальный вал длиной 3а (АВ=BD=DE=a), закрепленный подпятником А и подшипником D(рис. Д8,a), вращается с постоянной угловой скоростью ώ. К валу жестко прикреплен в точке Е ломаный однородный стержень массой m и длиной 10b, состоящий из двух частей 1 и 2, а в точке В прикреплен невесомый стержень длиной l=5bсточечной массой m3 на конце; оба стержня лежат в одной плоскости. 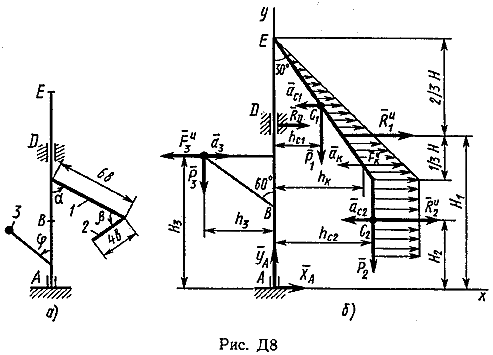 Дано: ώ=8 с-1, m=m1+m2=10 кг, m3=2 кг, =30°, β=150°, =60°, а=0,3 м, b=0,1 м. Определить: реакции подпятника А и подшипника D, пренебрегая весом вала. Решение. 1. Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках В и Е стержни (рис. Д8,б). Массы и веса частей 1 и 2ломаного стержня пропорциональны длинам этих частей и соответственно равны m1=0,6m; m2=0,4m; P1=0,6mg; P2=0,4mg; P3=m3g 2. Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси Ахутак, чтобы стержни лежали в плоскости ху, и изобразим действующие на систему силы: активные силы-силы тяжести Р1, Р2, Р3и реакции связей оставляющие реакции подпятника ХА, YАи реакцию цилиндрического подшипника несогласно принципу Даламбера, присоединим к этим силам силы инерции элементов однородного ломаного стержня и груза, считая его материальной точкой. Так как вал вращается равномерно, то элементы стержня имеют только нормальные ускорения аnk, направленные к оси вращения, а численно аnk=ώ2hk и, где hk-расстояния элементов от оси вращения. Тогда силы инерции Fик будут направлены от оси вращения, а численно 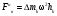 , где , где 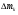 —масса элемента. Так как все Fикпропорциональны hk, то эпюры этих параллельных сил инерции стержня образуют для части 1треугольник, а для части 2-прямоугольник (рис. Д8,б). —масса элемента. Так как все Fикпропорциональны hk, то эпюры этих параллельных сил инерции стержня образуют для части 1треугольник, а для части 2-прямоугольник (рис. Д8,б).Каждую из полученных систем параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как модуль главного вектора сил инерции любого тела имеет значение Rи=тас, где т-масса тела, ас-ускорение его центра масс, то для частей стержня соответственно получим 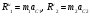 Сила инерции точечной массы 3должна быть направлена в сторону, противоположную ее ускорению и численно будет равна 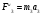 Ускорения центров масс частей 1 и 2стержня и груза 3равны: 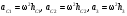 где hC1,hC2-расстояния центров масс частей стержня от оси вращения, а h3-соответствующее расстояние груза: 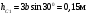 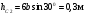 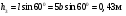 Подставив в (2) и (3) значения (4) и учтя (5), получим числовые значения Rи1 , Rи2 и Fи3 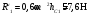 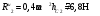 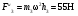 При этом линии действия равнодействующих Rи1и Rи2 пройдут через центры тяжестей соответствующих эпюр сил инерции. Так, линиядействия Rи1проходит на расстоянии 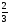 от вершины треугольника Е, где Н=6bcos30°. от вершины треугольника Е, где Н=6bcos30°.3. Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой плоской системы сил три уравнения равновесия. Получим 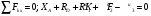 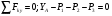 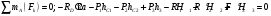 где H1, H2, Н3-плечи сил Rи1, Rи2,Fи3относительно точки А, равные (при подсчетах учтено, что Н=6bcos30°=0,52 м) 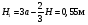 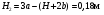 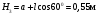 Подставив в уравнения (7) соответствующие величины из равенств (1), (5), (6), (8) и решив эту систему уравнений (7), найдем искомые реакции. Ответ: ХА=-33,7 Н; YA=117,7 Н; RD=-45,7. Н. Задача Д10. Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока (рис. Д10.0-Д10.9, табл. Д10). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: R1=0,2 м, r1=0,1 м, а шкива 2-R2=0,3 м, r2=0,15 м; их радиусы инерции относительно осей вращения равны соответственно ρ1=0,1 м и ρ2=0,2 м. Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса P1,…, Р6шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2изображать всегда как части системы). 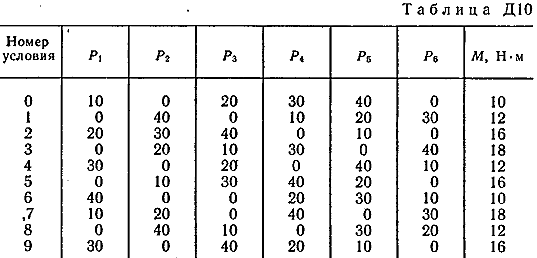
Пример Д10. Механическая система (рис. Д10) состоит из обмотанных нитями блока 1 радиуса R1и ступенчатого шкива 2(радиусы ступеней R2 и r2, радиус инерции относительно оси вращения ρ2), а также из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к блоку 1. Дано: P1=0, Р2=30 Н, Р3=40 Н, Р4=20 Н, М=16 Нм, R1=0,2 м, R2=0,3 м, r2=0,15 м, ρ2=0,2м. Определить: ускорение груза 3, пренебрегая трением. Решение. 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему - идеальные. Для определения а3 применим общее уравнение динамики: 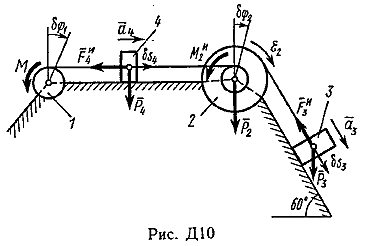 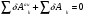 где 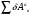 -сумма элементарных работ активных сил; -сумма элементарных работ активных сил; 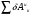 -сумма элементарных работ сил инерции. -сумма элементарных работ сил инерции.2. Изображаем на чертеже активные силы Р2,Р3, Р4 и пару сил с моментом М.Задавшись направлением ускорения а3,изображаем на чертеже силы инерции Fи3 , Fи4и пару сил инерции с моментом Ми2, величины которых равны: 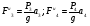 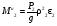 3. Сообщая системе возможное перемещение и составляя уравнение (1), получим 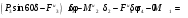 Выразим все перемещения через δ2: 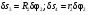 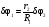 Подставив величины (2) и (4) в уравнение (3), приведем его к виду 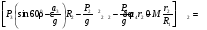 Входящие сюда величины έ2 и a4выразим через искомую величину а3: 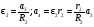 Затем, учтя, что δ2≠0, приравняем нулю выражение, стоящее в (5) в квадратных скобках. Из полученного в результате уравнения найдем 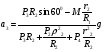 Вычисления дают следующий ответ: а3=-0,9 м/с2. Знак указывает, что ускорение груза 3и ускорения других тел направлены противоположно показанным на рис. Д10. |