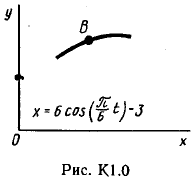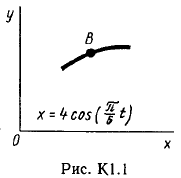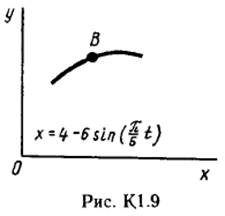КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех. Методические указания и контрольные задания для студентовзаочников технических специальностей высших учебных заведений
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
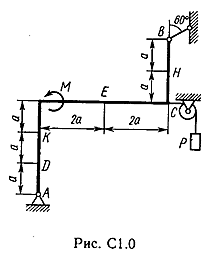
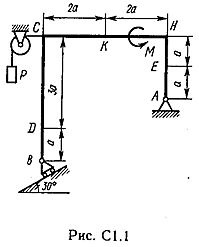
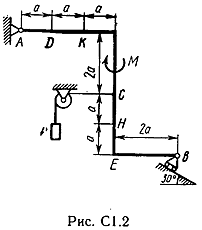
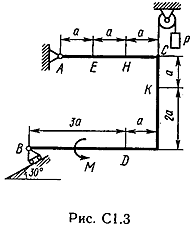
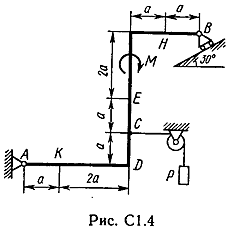
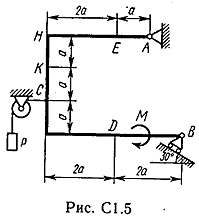
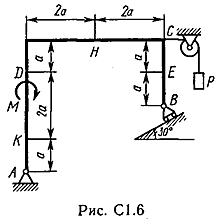
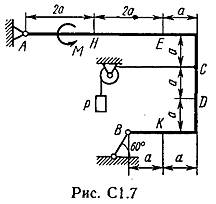
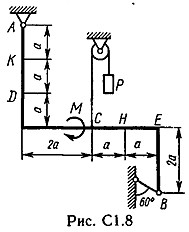
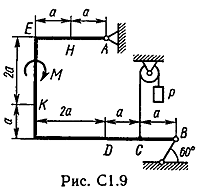
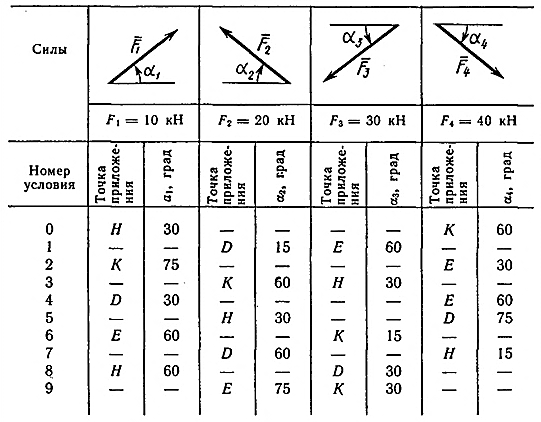
Задача С 1. Определение реакций связейЖесткая рама, расположенная в вертикальной плоскости (рис. С 1.0 – С 1.9, табл. С 1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действуют пара сил с моментом М = 100 кНм и две силы, значения, направления и точки приложения которых указаны в таблице. Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах, принять, а = 0,5 м.
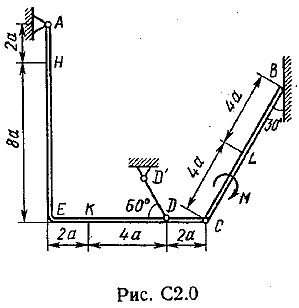
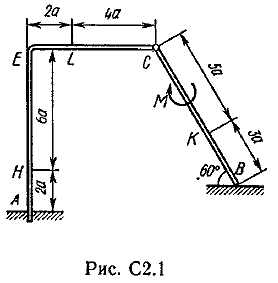
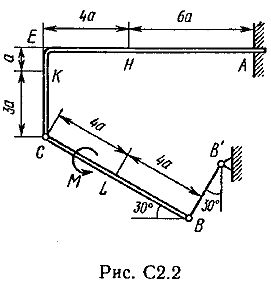
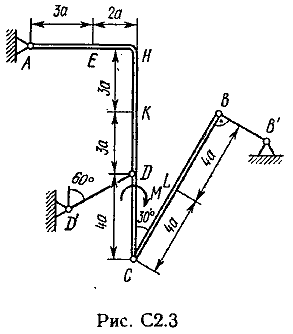
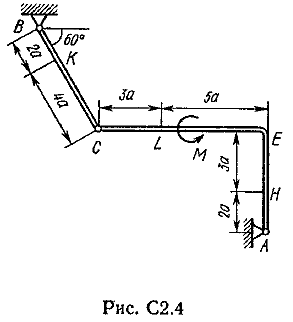
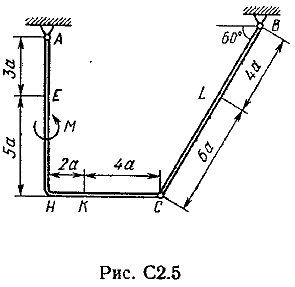
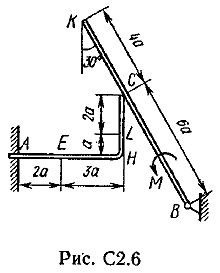
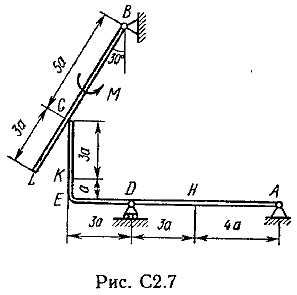
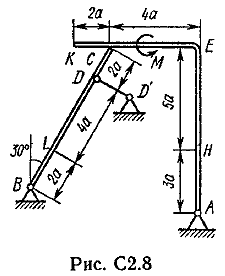
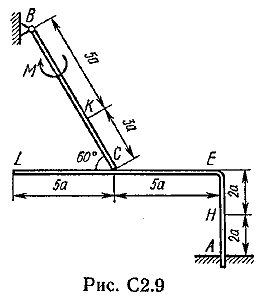
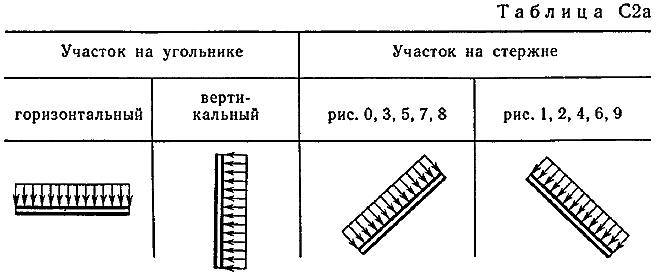
Пример C1. Жесткая пластина ABCD имеет в точке А неподвижную шарнирную опору, а в точке В подвижную шарнирную опору на катках. 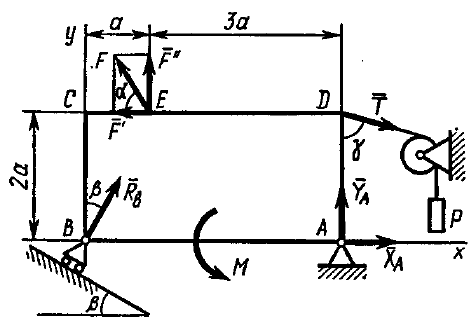 F = 25 кН, = 60°, Р = 18 кН, γ = 75°, М = 50 кН·м, β = 30°, а = 0,5 м. Определить: реакции в точках А и В. Решение. 1. Рассмотрим равновесие пластины. Заменим связи соответствующими реакциями: натяжение троса Т (по модулю Т = Р); шарнирно-неподвижную опору А двумя составляющими –ХА, YA, ; шарнирно-подвижную опору – RB. 2. Для плоской произвольной системы сил составим три уравнения равновесия. 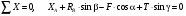 ; ;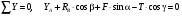 ; ;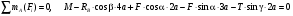 Подставив в составленные уравнения, числовые значения заданных величин и решив эти уравнения, определим искомые реакции: ХА= –8,5 кН; YА= –23,3 кН; RВ= 7,3 кН. Знаки указывают, что силы ХАи YА направлены противоположно показанным на рис. С 1. После нахождения реакций связей необходимо выполнить проверку с помощью другого уравнения равновесия. Например, определить сумму моментов всех сил относительно точки С. Если равенство окажется равным нулю, то значения найденных реакций, определены, верно. 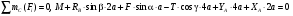 . .Задача С 2. Определение реакции связей составной конструкции Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно (рис. С 2.0 – С 2.5), или свободно опираются друг о друга (рис. С 2.6 – С 2.9). Внешними связями, наложенными на конструкцию, являются в точке А или шарнир, или жесткая заделка; в точке В или гладкая плоскость (рис. 0 и 1), или невесомый стержень ВВ' (рис. 2 и 3), или шарнир (рис. 4–9); в точке Dили невесомый стержень DD' (рис. 0, 3, 8), или шарнирная опора на катках (рис. 7). На каждую конструкцию действуют: пара сил с моментом М=60 кНм, равномерно распределенная нагрузка интенсивности q=20 кН/м и еще две силы, их направления и точки приложения указаны в табл. С 2; там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила F2 под углом 60° к горизонтальной оси, приложенная в точке L, сила F4под углом 30° к горизонтальной оси, приложенная в точке Е, и нагрузка, распределенная на участке СК). Определить реакции связей в точках А, В, С (для рис. 0, 3, 7, 8 еще и в точке D), вызванные заданными нагрузками. При окончательных расчётах, принять, а=0,2 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С 2а.
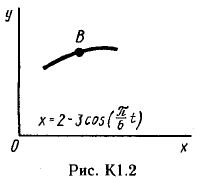
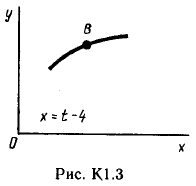
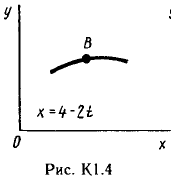
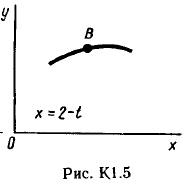
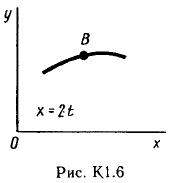
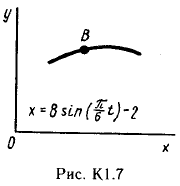
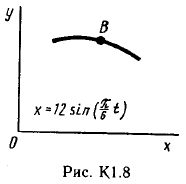
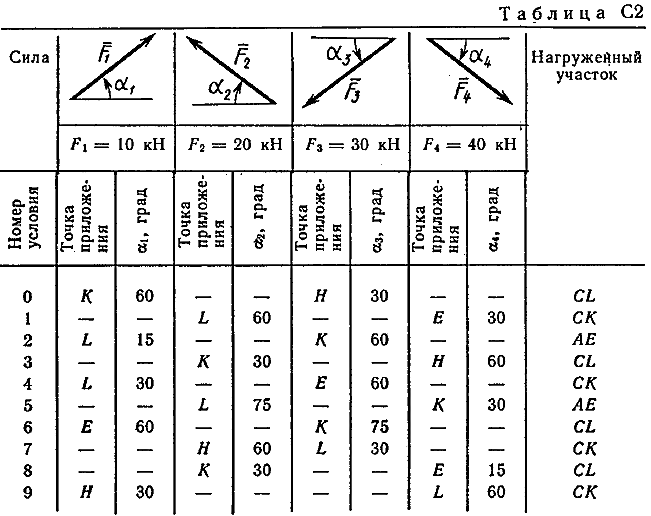 Пример С 2. На угольник ABC ( АВС=90°), конец А которого жестко заделан, в точке С опирается стержень DE(рис. С 2, а).Стержень имеет в точке Dнеподвижную шарнирную опору и к нему приложена сила F, а к угольнику – равномерно распределенная на участке KBнагрузка интенсивности qи пара с моментом М. 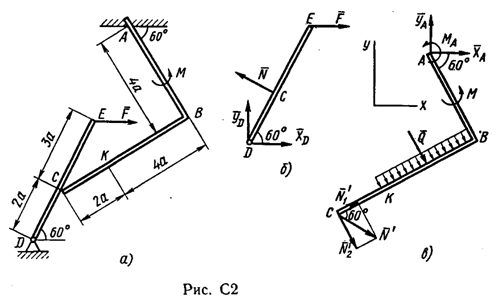 Дано: F=10 кН, М=5 кНм, q=20 кН/м, а=0,2 м. Определить: реакции в точках А, С, D, вызванные заданными нагрузками. Решение. 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE(рис. С 2, б). Проведем координатные оси ХYи изобразим действующие на стержень силы: силу F, реакцию N, направленную перпендикулярно стержню, и составляющие XDи YDреакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия: 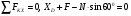 ; ;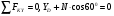 ; ;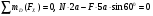 . .2. Рассмотрим равновесие угольника (рис. С 2, в).На него действуют сила давления стержня N', направленная противоположно реакции N, равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка KB(численно Q=q·4a=16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими ХА, YА, и пары с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия: 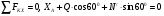 ; ;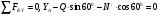 ; ;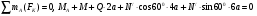 . .При вычислении момента силы N' разлагаем её на составляющие N/1и N/2и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений, найдем искомые реакции. При решении учитываем, что численно N'=N всилу равенства действия и противодействия. Ответ: N= 21,7 кН, YD= –10,8 кН; XD= 8,8 кН, ХА= –26,8 кН, YA= 24,7 кН, МА= 42,6 кНм. Знаки указывают, что силы YD, ХАи момент МАнаправлены противоположно показанным на рисунках. Задача К 1. Определение скорости и ускорения точки по заданным уравнениям движения. Задача К 1а. Точка В движется в плоскости ху (рис. К 1.0 – К 1.9, табл. К 1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х=f1(t), у=f2(t), где х и у выражены в сантиметрах, t – в секундах. Найти уравнение траектории точки; для момента времени t1=1 с, определить скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Зависимость х=f1(t) указана непосредственно на рисунках, а зависимость у=f2(t) дана в табл. К 1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задачах C 1С 4, номер рисунка выбирается по предпоследней цифре шифра; а номер условия в табл. К 1-по последней. Задача К 1б. Точка движется по дуге окружности радиуса R=2м по закону s=f(t), заданному в табл. К 1 в столбце 5 (s– в метрах, t – в секундах), где s=AM – расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1=1 с. Изобразить на рисунке векторы υ и , считая, что точка в этот момент находится в положении М, а положительное направление отсчета sот А к М. 
Пример К 1а. По заданным уравнениям движения точки М в координатной форме определить: траекторию её движения в заданный момент времени t=1c, найти скорость и ускорение. 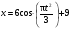 (см), (см),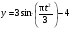 (см). (см).Решение: 1. Определим траекторию движущейся точки М. Для получения уравнения траектории движущейся точки исключим из заданных уравнений параметр времени t: 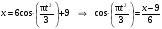 , ,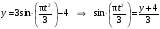 . .Полученные уравнения возведем в квадрат и суммируем: 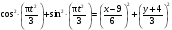 . .Таким образом, 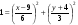 . .Данное выражение представляет собой траекторию движущейся точки М – уравнение эллипса с центром в точке с координатами (9; -4). Построим траекторию в координатных осях ху (рис.9). Укажем положение точки М на траектории в заданный момент времени, для этого подставим время t=1с, в уравнения: 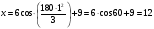 см, см,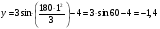 см. см.Тогда точка М с координаты (12; -1,4). Для указания положительного отсчета по траектории определим положение точки М в начальный момент времени при t=0 с. 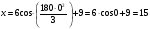 см, см,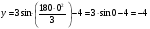 см. см.Тогда точка М0 имеет координаты (15; - 4). Точки М и М0 принадлежат траектории эллипса, следовательно, решение верно. Направление положительного отсчета по траектории идёт от точки М0 в момент времени t=0 c, к точке М, когда t=1 с (против движения часовой стрелки). 2. Определим скорость точки М в заданный момент времени t. Известно, что скорость можно разложить по проекциям на координатные оси: 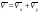 . .Определим проекцию скорости точки М на ось Ох: 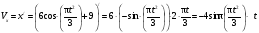 . .В заданный момент времени t=1 с, проекция скорости составит: 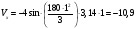 см/с. см/с.Так, как Vx= 10,9<0, то вектор скорости 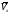 направлен из точки М параллельно оси Ох в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе скоростей, указанных на схеме. направлен из точки М параллельно оси Ох в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе скоростей, указанных на схеме. Определим проекцию скорости точки М на ось Оу: 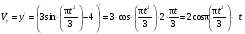 . .В заданный момент времени t=1 с, проекция скорости составит: 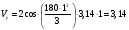 см/с. см/с.Так, какVy=3,14>0, то вектор скорости 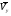 направлен из точки М параллельно оси Оу в сторону положительных значений у, данный вектор требуется отложить в том же масштабе, что и вектор направлен из точки М параллельно оси Оу в сторону положительных значений у, данный вектор требуется отложить в том же масштабе, что и вектор 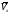 . .Геометрическая сумма векторов 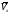 и и 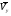 (по правилу параллелограмма) представляет собой вектор скорости (по правилу параллелограмма) представляет собой вектор скорости 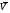 точки М в заданный момент времени, этот вектор должен быть направлен по касательной τ к траектории движения (рис.10). Численное значение скорости точки М в заданный момент времени, этот вектор должен быть направлен по касательной τ к траектории движения (рис.10). Численное значение скорости 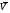 можно измерить, согласно указанному масштабу для векторов скоростей, либо определить по теореме Пифагора (так как вектора можно измерить, согласно указанному масштабу для векторов скоростей, либо определить по теореме Пифагора (так как вектора 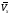 и и 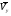 взаимно перпендикулярны): взаимно перпендикулярны):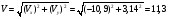 см/с. см/с.3. Определим ускорение точки М в заданный момент времениt. Известно, что ускорение можно разложить по проекциям на координатные оси: 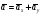 . .Определим проекцию ускорения точки М на ось Ох: 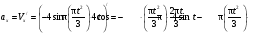 . .В заданный момент времени t=1с, проекция ускорения составит: 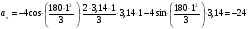 см/с2. см/с2.Так, как 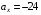 <0, то вектор ускорения <0, то вектор ускорения 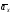 направлен из точки М параллельно оси Ох в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе ускорений, указанного на схеме. направлен из точки М параллельно оси Ох в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе ускорений, указанного на схеме.Определим ускорение скорости точки М на ось Оу: 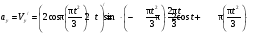 . .В заданный момент времени t= 1с, проекция ускорения составит: 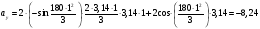 см/с2. см/с2.Так, как 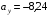 <0, то вектор ускорения <0, то вектор ускорения 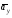 направлен из точки М параллельно оси Оу в сторону отрицательных значений у, данный вектор требуется отложить в том же масштабе, что и вектор направлен из точки М параллельно оси Оу в сторону отрицательных значений у, данный вектор требуется отложить в том же масштабе, что и вектор 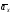 . .Геометрическая сумма векторов 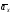 и и 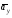 (по правилу параллелограмма) представляет собой вектор ускорения (по правилу параллелограмма) представляет собой вектор ускорения 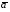 точки М в заданный момент времени: точки М в заданный момент времени: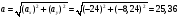 см/с2. см/с2.Определим касательное ускорение точки М в заданный момент времени t, зная проекции скорости и ускорения на оси координат: 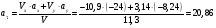 см/с2. см/с2.Так, как 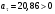 , то вектор ускорения , то вектор ускорения 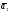 направлен из точки М по касательной к траектории движения в сторону направления вектора скорости направлен из точки М по касательной к траектории движения в сторону направления вектора скорости 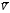 (движение точки будет ускоренным), данный вектор требуется отложить в масштабе ускорений. (движение точки будет ускоренным), данный вектор требуется отложить в масштабе ускорений.Определим нормальное ускорение точки М в заданный момент времени t, зная полное и касательное ускорения: 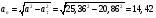 см/с2. см/с2.Вектор ускорения 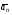 направлен из точки М по нормали п к траектории движения к центру кривизны траектории, данный вектор требуется отложить в масштабе ускорений. направлен из точки М по нормали п к траектории движения к центру кривизны траектории, данный вектор требуется отложить в масштабе ускорений. Так, как векторная сумма ускорений 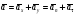 справедлива, то решение верно. справедлива, то решение верно.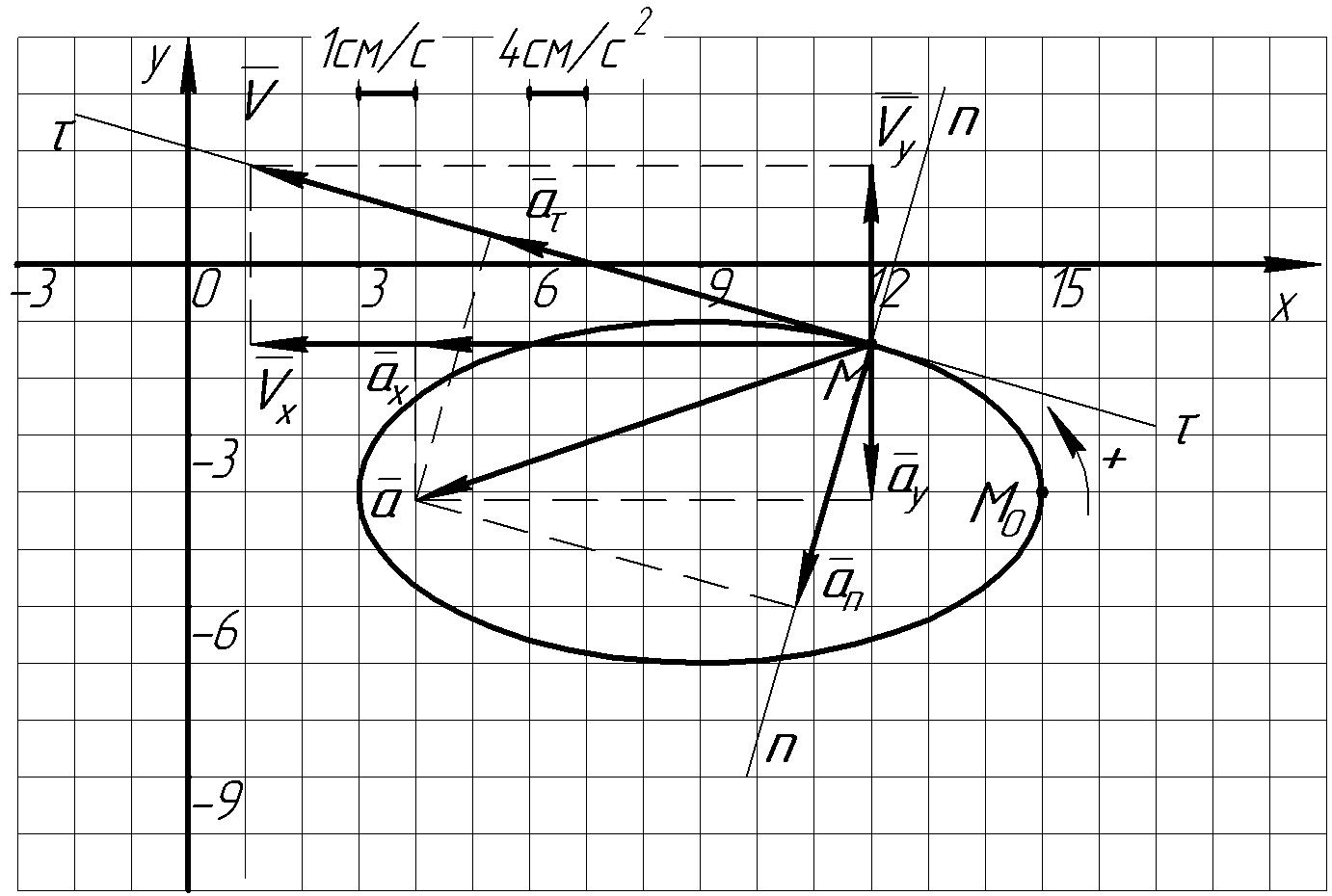 Определим радиус кривизны траектории 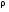 в заданный момент времени c учетом нормального (центростремительного) ускорения в заданный момент времени: в заданный момент времени c учетом нормального (центростремительного) ускорения в заданный момент времени: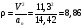 см. см. | ||||||||||||||||||||||||||||||||||||||||