КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех. Методические указания и контрольные задания для студентовзаочников технических специальностей высших учебных заведений
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
|
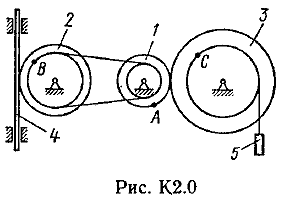
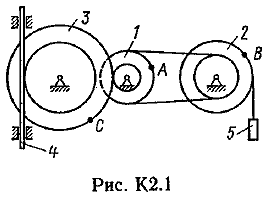
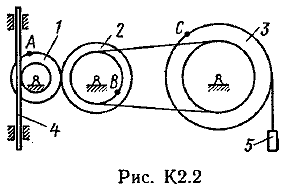
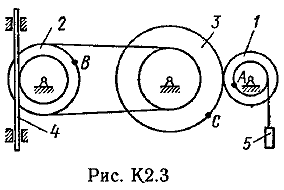
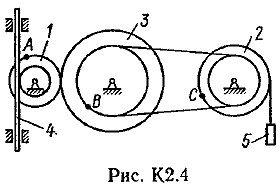
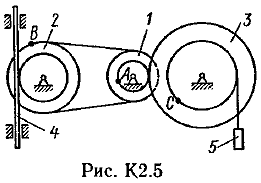
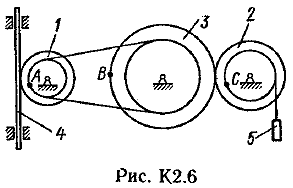
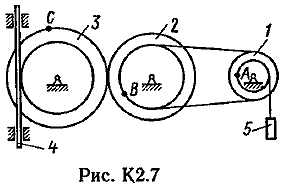
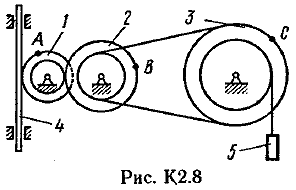
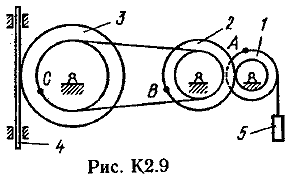
Пример К 1б. Точка движется по дуге окружности радиуса R=2 м по закону 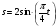 (s-в метрах, t-в секундах), где sAM(рис. К 1б). Определить скорость и ускорение точки в момент времени t1=1 с. (s-в метрах, t-в секундах), где sAM(рис. К 1б). Определить скорость и ускорение точки в момент времени t1=1 с.Решение. Определяем скорость точки: 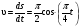 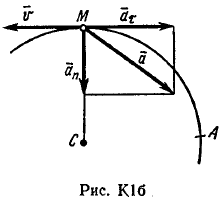 При t1=1 с, получи 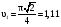 м/с. м/с.Ускорение находим по его касательной и нормальной составляющим: 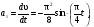 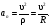 При t1=1 с, получим, учитывая, что R=2 м, 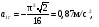 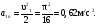 Тогда ускорение точки при t1=1 с, будет: 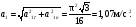 Изобразим на рис. К 1б векторы  и и  учитывая знаки υ1 и а1 и считая положительным направление от А к М. учитывая знаки υ1 и а1 и считая положительным направление от А к М.Задача К2. Механизм состоит из: ступенчатых колес 1–3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0-К2.9, табл. К2). Радиусы ступеней колес равны соответственно: у колеса 1 – r1=2 см, R1=4 см, у колеса 2 – r2=6 см, R2=8 см, у колеса 3 – r3=12 см, R3=16 см. На ободьях колес расположены точки А, В и С. В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где 1(t) – закон вращения колеса 1, s4(t) – закон движения рейки 4, 2(t) – закон изменения угловой скорости колеса 2, υ5(t) – закон изменения скорости груза 5 и т. д. (везде выражено в радианах, s – в сантиметрах, t – в секундах). Положительное направление для и против хода часовой стрелки, для s4, s5 и υ4,υ5 – вниз. Определить в момент времени t1=2с, указанные в таблице в столбцах «Найти» скорости (υ– линейные, – угловые) и ускорения (а – линейные, ε – угловые) соответствующих точек или тел (υ5 – скорость груза 5 и т. д.).
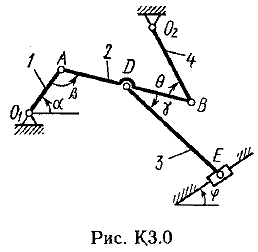
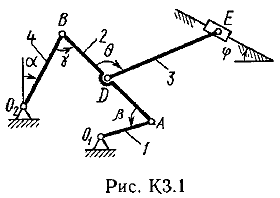
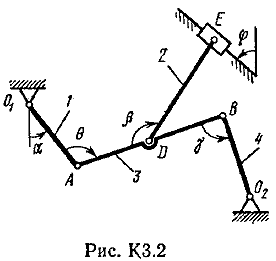
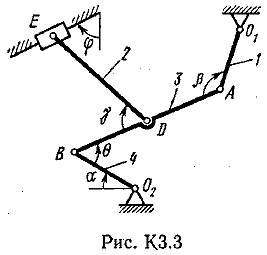
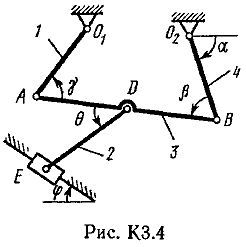
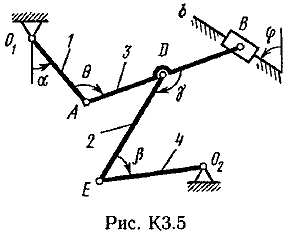
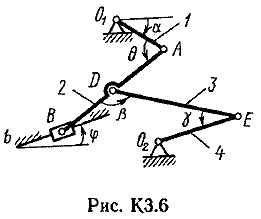
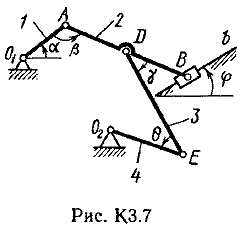
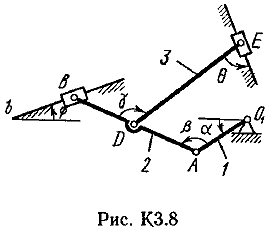
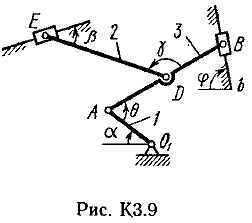
 Пример К2. Рейка 1, ступенчатое колесо 2с радиусами R2=6 см и r2=4 сми колесо 3радиуса R3=8 см, скрепленное с валом радиуса r3=3 см, находятся в зацеплении; на вал намотана нить с грузом 4на конце (рис. К2). Рейка движется по закону s1=3t3 см. Определить: 3, υ4,ε3, в момент времени t=t1=3 си ускорениеaA точки А обода колеса 3. 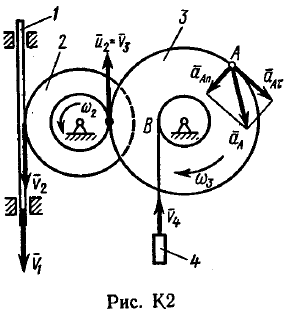 Решение. 1. Определить угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость: 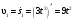 (1). (1).Так, как рейка и колесо 2находятся в зацеплении, то υ2=υ1или 2R2=υ1. Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, υ2=υ3или 2r2=3R3. Из этих равенств находим: 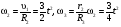 (2). (2).Тогда, для момента времени t1=3 с, получим 3=6,75 с-1. 2. Определить ε3. Учитывая второе из равенств (2), 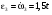 . Тогда при t1=3с: . Тогда при t1=3с:ε3=4,5 с-2. 3. Определить υ4. Так как υ4=υB=3r3,то при t1=3 с υ4=20,25 см/с. 4. Определить аА.Для точки А аА=аА+аАn,где численно аА=R3ε3, аАn=R332. Тогда, для момента времени t1=3 с: аА=36 см/с2 , аАn=364,5 см/с2, 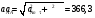 см/с2. см/с2.Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2. Ответ: 3=6,75 с-1; υ4=20,25 см/с; ε3=4,5 с-2; аА=366,3 см/с2. Задача К З. Плоский механизм состоит из стержней 1, 2, 3, 4иползуна В или Е (рис. К З.0К 3.7) или из стержней 1,2,3и ползунов В и Е (рис. К 3.8, К 3.9), соединенных друг с другом и с неподвижными опорами О1О2 шарнирами; точка Dнаходится в середине стержня АВ. Длины стержней равны соответственно: l1=0,4 м, l2=1,2 м, l3=1,4 м, l4=0,6 м. Положение механизма определяется углами , β, γ, , θ. Значения этих углов и других заданных величин, указаны в табл. К 3а (для рис. 0-4) или в табл. К 3б (для рис. 5-9); при этом в табл. К За 1 и 4величины постоянные. Определить величины, указанные в таблицах в столбцах «Найти». Дуговые стрелки, на рисунках, показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол γ на рис. 8 следует отложить от DBпо ходу часовой стрелки, а на рис. 9против хода часовой стрелки и т. д.). Построение чертежа начинать со стержня, направление которого определяется углом ; ползун с направляющими для большей наглядности изобразить так, как в примере К 3 (см. рис. К 3б). Заданные, угловую скорость и угловое ускорение, считать направленными против часовой стрелки, а заданные скорость υВ и ускорение аВ от точки В к b (на рис. 5-9). 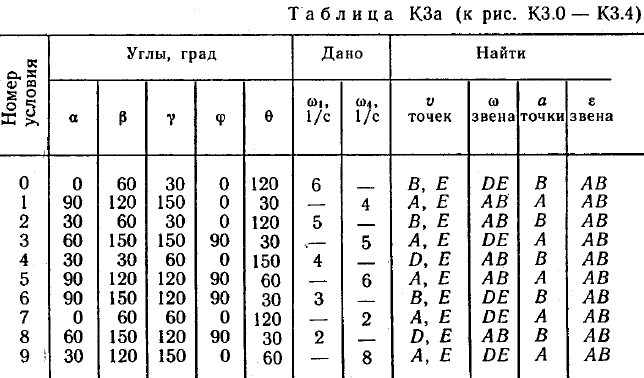 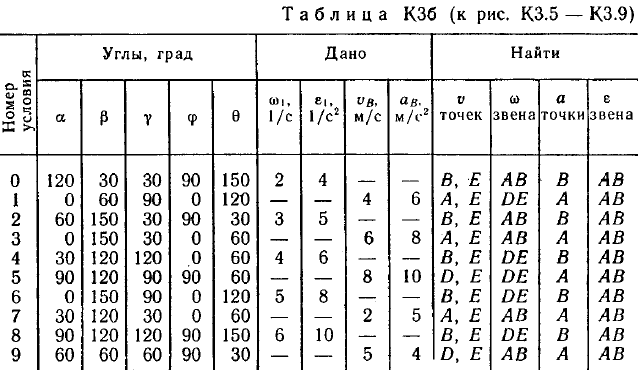
Пример КЗ. Механизм (рис. К 3а) состоит из стержней 1, 2, 3, 4и ползуна В, соединенных друг с другом и с неподвижными опорами О1и О2 шарнирами. 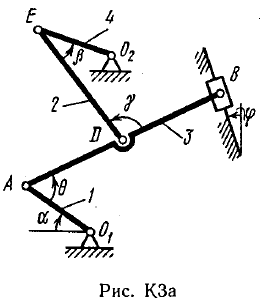 Дано: =60°, β=150°, γ=90°, =30°, θ=30°, AD=DB, l1=0,4м, l2=1,2 м, l3=1,4 м, ώ1=2 с-1, έ=7 с-2 (направления (ώ1 и έ1против хода часовой стрелки). Определить: υB, υE , ώ2, аB, έ3. Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К 3б; на этом рисунке изображаем все векторы скоростей). 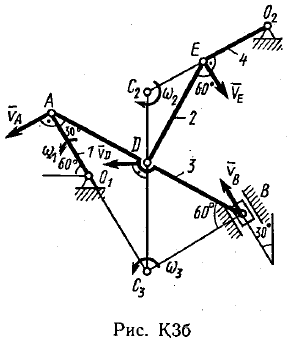 2. Определяем υB. Точка В принадлежит стержню АВ. Чтобы найти υB, надо знать скорость какой-нибудь другой точки этого стержня и направление υB. По данным задачи, учитывая направление ώ1, можем определить υА, численно: 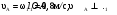 Направление υВнайдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная υАи направление υB, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор υB(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим: 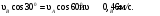 3. Определяем υЕ. Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить υЕ,надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная υA и υB, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С3, лежащая на пересечении перпендикуляров к υА и υB, восставленных из точек А и В (к υАперпендикулярен стержень 1). По направлению вектора υA определяем направление поворота стержня АВ вокруг МЦС С3. Вектор υD перпендикулярен отрезку C3D, соединяющему точки D и С3, и направлен в сторону поворота. Величину υD найдем из пропорции: 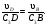 Чтобы вычислить С3D и С3В, заметим, что ∆AС3Впрямоугольный, так как острые углы в нем равны 30° и 60°, и что С3В=АBsin30°=0,5АВ=BD. Тогда ∆ВС3D является равносторонним и С3В=C3D. В результате равенство дает: 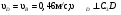 Так как точка Е принадлежит одновременно стержню О2Е, вращающемуся вокруг О2, то υЕ О2E. Тогда, расставляя из точек Е и Dперпендикуляры к скоростям υЕи υD,построим МЦС С2стержня DE. По направлению вектора υDопределяем направление поворота стержня DEвокруг центра С2. Вектор υEнаправлен в сторону поворота этого стержня. Из рис. К 3б видно, что C2ED=C2DE=30°, откуда С2Е=C2D. Составив теперь пропорцию, найдем, что: 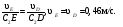 4. Определяем ώ2. Так, как МЦС стержня 2известен (точка С2)и 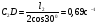 , то , то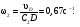 5. Определяем аВ(рис. К 3в, на котором изображаем все векторы ускорений). Точка В принадлежит стержню АВ. Чтобы найти аВ, надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить aА=aА+aАn, где численно: 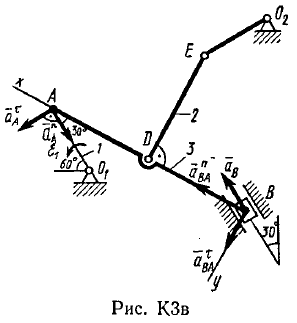 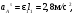 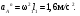 Вектор аАnнаправлен вдоль АО1,а аАперпендикулярно АО1изображаем эти векторы на чертеже (см. рис. К 3в). Так, как точка В одновременно принадлежит ползуну, то вектор аBпараллелен направляющим ползуна. Изображаем вектор аBна чертеже, полагая, что он направлен в ту же сторону, что и υB. Для определения аBвоспользуемся равенством: 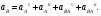 Изображаем на чертеже векторы аnВА(вдоль ВА от B к A) и аВА(в любую сторону перпендикулярно ВА); численно аnB=ώ23l.Найдя ώ3 с помощью построенного МЦС С3 стержня 3, получим: 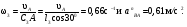 Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения аВи аВА,их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси. Чтобы определить аВ, спроектируем обе части равенства (8) на направление ВА (ось х),перпендикулярное неизвестному вектору аВА. Тогда получим: 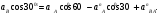 Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что: aB=0,72 м/с2. Так, как получилось aВ>0, то, следовательно, вектор аВнаправлен, как показано на рис. К Зв. 6. Определяем έ3. Чтобы найти έ3, сначала определим аВА. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим: 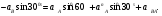 Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что аВА=3,58 м/с2. Знак указывает, что направление аВАпротивоположно показанному на рис. К 3в. Теперь из равенства аВА=έ3l3 получим: 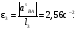 | ||||||||||||||||||||||||||||