КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех. Методические указания и контрольные задания для студентовзаочников технических специальностей высших учебных заведений

• Название: Методические указания и контрольные задания для студентовзаочников технических специальностей высших учебных заведений
• Анкор: КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех.docx
• Дата: 13.12.2017
• Размер: 2.5 Mb.
• Имя файла: КОНТРОЛЬНЫЕ ЗАДАНИЯ С ПРИМЕРАМИ _ТерМех.docx
• Тип: Методические указания; #11295
• страница: 6 из 7

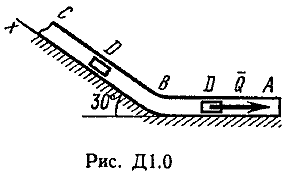
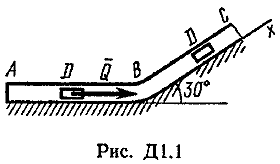
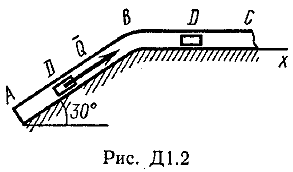
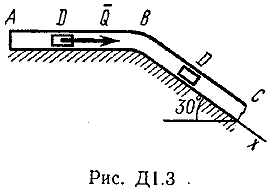
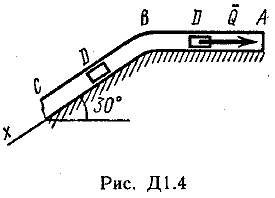
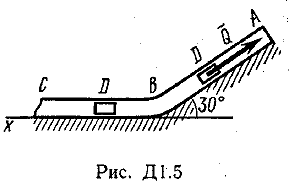
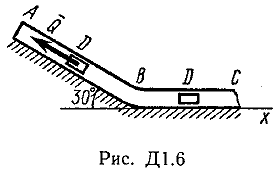
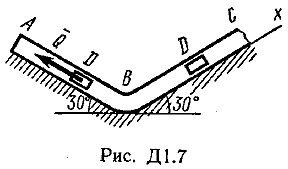
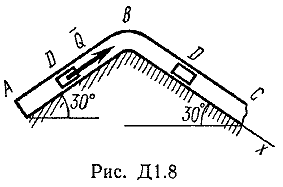
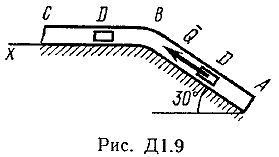
Указания.

Задача Д1 — на составление и интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить векторное уравнение движения точки (груза) на участке АВ, спроектировать это уравнение на координатную ось, направленную вдоль АВ, и проинтегрировать полученное дифференциальное уравнение методом разделения переменных, учитывая начальные условия (вторая задача динамики точки). Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС.

Посте этого нужно составить векторное уравнение движения точки на участке ВС и спроектировать это уравнение на 2 координатные оси, направленные вдоль ВС и перпендикулярно ВС. Затем проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t = 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти в уравнении от переменных V_x, t к переменным V_х, x, учитывая, что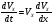



Груз D массой m, получив в точке А начальную скорость υ₀, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9, табл. Д1).

На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости υ груза (направлена против движения) ; трением груза о трубу на участке АВ пренебречь.

В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f=0,2) и переменная сила F, проекция которой F_x на ось х задана в таблице.

Считая груз материальной точкой и зная расстояние АВ=l или время t₁движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. х=f(t), где х=BD.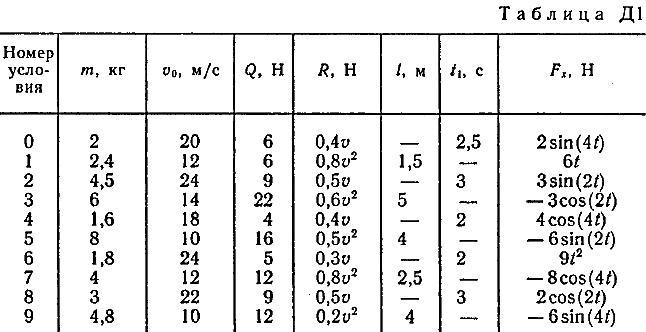



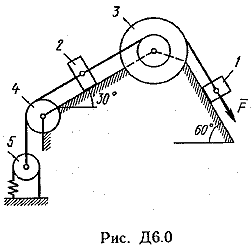
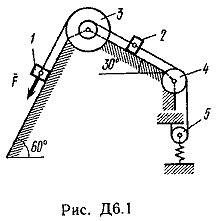
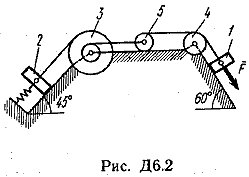
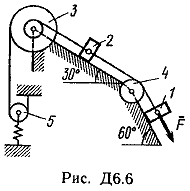
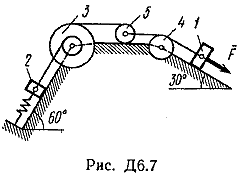
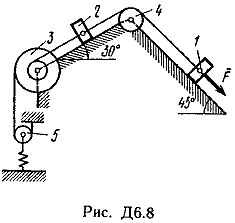
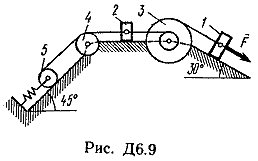
Пример Д1.

На вертикальном участке АВ трубы (рис. Д1) на груз Dмассой т действуют сила тяжести и сила сопротивления R; расстояние от точки А, где υ=υ₀, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F=F(t), заданная в ньютонах.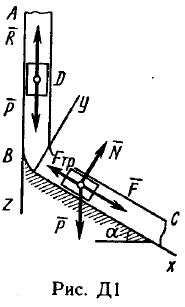

Дано: m=2 кг, R=υ²,где =0,4 кг/м, υ₀=5 м/с, l=2,5 м, Fx=16sin(4t).

Определить: х=f(t)-закон движения груза на участке ВС.

Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы Р=mgи R. Проводим ось Аzи составляем дифференциальное уравнение движения груза в проекции на эту ось: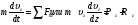



Далее находим Р_z=Р=mg, R_z=-R=-υ², подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что υ_z=υ, получим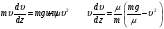



Введем для сокращения записей обозначения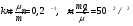



где при подсчете принято g=10 м/с². Тогда уравнение (2) можно представить в виде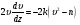



Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим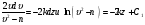



По начальным условиям при z=0 υ=υ₀, что дает С₁=ln(υ²₀-п) и из равенства (5) находим ln(υ²-п) =-2kz+ln(υ²₀-п) или 1n(υ²-п)-ln (υ²₀-n)=-2kz. Отсюда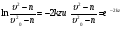



В результате находим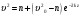



Полагая в равенстве (6) z=l= 2,5 м и заменяя kи п их значениями (3), определим скорость υ_Bгруза в точке В (υ_о=5 м/с, число е=2,7):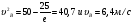



2. Рассмотрим теперь движение груза на участке ВС; найденная скорость υ_Вбудет для движения на этом участке начальной скоростью (υ₀=υ_В). Изображаем груз (в произвольном положении) и действующие на него силы Р=mg,N,F_три F. Проведем из точки В оси Вх и Byи составим дифференциальное уравнение движения груза в проекции на ось Вх: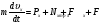



или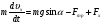



где F_тp=fN. Для определения N составим уравнение в проекции на ось B_y. Так как а_у=0, получим 0=N-mgcos, откуда N=mgcos. Следовательно, F_тр=fmgcos; кроме того, F_x=16sin(4t) и уравнение (8) примет вид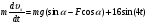



Разделив обе части равенства на т, вычислим g(sin-fcos)=g(sin30°-0,2cos30°)=3,2; 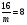и подставим эти значения в (9). Тогда получим



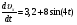Умножая обе части уравнения (10) на dtи интегрируя, найдем

υ_x=3,2t-2cos(4t)+C₂

Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 υ=υ₀=υ_B, где υ_Bдаётся равенством (7). Подставляя эти величины в (11), получим

C₂=υ_B+2cos0=6,4+2=8,4

При найденном значении С₂ уравнение (11) дает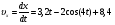



Умножая здесь обе части на dtи снова интегрируя, найдем

x=1,6t²+8,4t+C₃

Так как при t=0 х=0, то С₃=0 и окончательно искомый закон движения груза будет

x=1,6t²+8,4t+0,5sin(4t)

где х-в метрах, t-в секундах.

Задача Д2.

Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3с радиусами ступеней R₃=0,3 м, r₃=0,1 м и радиусом инерции относительно оси вращения ρ₃=0,2 м, блока 4радиуса R₄=0,2 м и катка (или подвижного блока) 5 (рис. Д6.0-Д6.9, табл. Д6); тело 5считать сплошным однородным цилиндром, а массу блока 4-равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f=0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3(или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.

Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).

Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s₁=0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ₁, υ₂, υ_C5-скорости грузов 1, 2 ицентра масс тела 5 соответственно, ώ₃ и ώ₄-угловые скорости тел 3и 4.

Все катки, включая и катки, обмотанные нитями (как, например, каток 5на рис. 2), катятся по плоскостям без скольжения.

На всех рисунках не изображать груз 2, если т₂=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.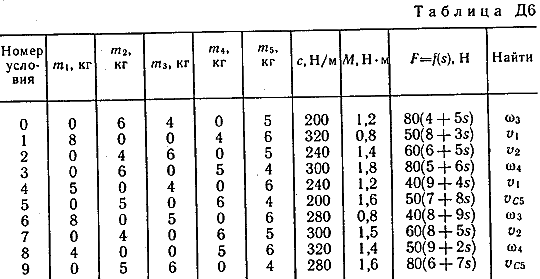



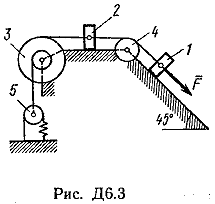
Пример Д6.

Механическая система (рис. Д6, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3с радиусами ступеней R₃ и r₃и радиусом инерции относительно оси вращения ρ₃, блока 4и груза 5 (коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю.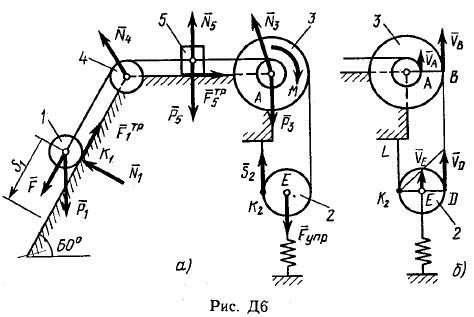

Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3при движении действует постоянный момент М сил сопротивления.

Дано: m₁=8 кг, т₂=0, т₃=4 кг, m₄=0, т₅=10 кг, R₃=0,3 м, r₃=0,1 м, ρ₃=0,2 м, f=0,1, с=240 Н/м, М=0,6 Нм, F=20(3+2s) Н, s₁=0,2 м.

Определить: ώ₃ в тот момент времени, когда s=s₁.

Решение.

1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 иневесомых тел 2, 4,соединенных нитями. Изобразим действующие на систему внешние силы: активные F, F_упр, Р₁, Р₃, Р₅, реакции N₁, N₃, N₄, N₅, натяжение нити S₂, силы трения F₁^тр, F₅^три момент М.

Для определения ώ₃ воспользуемся теоремой об изменении кинетической энергии: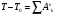



2. Определяем То и Т. Так как в начальный момент система находилась в покое, то Т₀=0. Величина Т равна сумме энергий всех тел системы: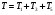



Учитывая, что тело 1 движется плоскопараллельно, тело 5-поступательно, а тело 3вращается вокруг неподвижной оси, получим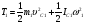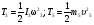





Все входящие сюда скорости надо выразить через искомую ώ₃. Для этого предварительно заметим, что υ_c1=υ₅=υ_А, где А-любая точка обода радиуса r₃шкива 3и что точка K₁-мгновенный центр скоростей катка 1, радиус которого обозначим r₁. Тогда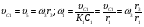



Кроме того, входящие в (3) моменты инерции имеют значения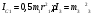



Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно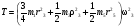



3. Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь s₁. Введя обозначения: s₅-перемещение груза 5 (s₅=s₁), ₃-угол поворота шкива 3, λ₀и λ₁-начальное и конечное удлинения пружины, получим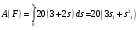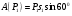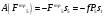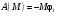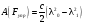











Работы остальных сил равны нулю, так как точки K₁и К₂, где приложены силы N₁F^тр₁и S₂-мгновенные центры скоростей; точки, где приложены силы Р₃,N₃и Р₄-неподвижны; а реакция N₅перпендикулярна перемещению груза.

По условиям задачи, λ₀=0. Тогда λ₁=s_Е, где s_Е-перемещение точки Е (конца пружины). Величины s_Eи ₃ надо выразить через заданное перемещение s₁; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда так как 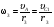(равенство υ_С1=υ_Aуже отмечалось), то и.

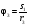Далее, из рис. Д6, б видно, что υ_D=υ_B=ώ₃R₃, а так как точка К₂является мгновенным центром скоростей для блока 2(он как бы «катится» по участку нити K₂L), то υ_E=0,5υ_D=0,5ώ₃R₃; следовательно, иλ₁=s_E=0,5₃R₃=0,5s₁R₃/r₃. При найденных значениях ₃ и λ₁для суммы вычисленных работ получим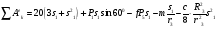



Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т₀=0, придем к равенству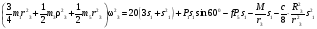



Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость ώ₃.