контрольная математика. Кр Э-1з (2). Методические указания и контрольные задания для студентов
 Скачать 65.61 Kb. Скачать 65.61 Kb.
|
|
ГОСУДАРСТВЕННОЕ бюджетное профессиональное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ “Себряковский технологический техникум” Математика методические указания и контрольные задания для студентов заочного отделения образовательного учреждения СПО по специальности 08.02.09 Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий Основная задача дисциплины «Математика» для средних специальных учебных заведений состоит в том, чтобы дать студентам комплекс математических знаний, умений, необходимых для изучения смежных и специальных дисциплин, для использования в практической деятельности для развития логического мышления. Общие методические указания Данное пособие ставит своей целью оказание помощи студентам заочной формы обучения в организации самостоятельной работы над учебным материалом. Она складывается из чтения учебников, лекций, решения задач, выполнения контрольной работы. Кроме того, студент может обращаться к преподавателю с письменными и устными вопросами. Рекомендуем придерживаться следующих советов: Внимательно изучите цель, поставленную в задаче; выявите, какие теоретические положения вам необходимы. Попытайтесь соотнести данную задачу к какому либо типу задач, способ решения которых вам известен. Решения задач и примеров следует записывать подробно, вычисления должны располагаться в строгом порядке. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если же чертежи требуют тщательного выполнения, то их нужно выполнять с использованием чертежных инструментов, соблюдая масштаб. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. Затем в полученную формулу представляют числовые значения (если таковы даны). Требование к выполнению и оформлению контрольной работы Контрольная работа выполняется в отдельной тетради школьного формата. На обложке тетради должен быть приклеен титульный лист утвержденного образца или аккуратно записаны все данные: шифр, фамилия, имя, отчество, предмет. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво. Решение задач располагать в порядке по нумерации, условия должны быть обязательно полностью переписаны, записан ответ. Решение задач должны сопровождаться кратким, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать. Вариант работы соответствует последней цифре шифра. Контрольные работы должны быть выполнены в срок. В период сессии работы на проверку не принимаются. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки. Студенты, не имеющие зачет по контрольной работе, к экзамену не допускаются. Тематический план Тема №1. Теория пределов Пределы, основные свойства пределов. Бесконечно малые и бесконечно большие величины и их свойства. Эквивалентные бесконечно малые. Первый и второй замечательные пределы. Примеры вычисления приделов Тема №2. Дифференциальное исчисление. Определение производной, геометрический смысл. Производная сложной функции. Основные правила дифференцирования. Уравнение касательной и нормали. Нахождение асимптот графика. Выпуклость и вогнутость графика функции. Решение систем уравнений методом Крамера. В результате изучения темы студент должен Знать: - определение предела функции в точке и бесконечности; - понятие бесконечно малых и бесконечно больших величин; - основные правила дифференцирования; - уравнение нормали и касательной; - достаточное условие выпуклости, вогнутости; Уметь: - вычислять пределы всеми способами; - применять основные правила дифференцирования; - уметь проводить исследования функции. Тема №3.неопределенный интеграл, его свойства. Первообразная. Неопределенный интеграл, его простейшие свойства. Таблица основных интегралов. Интегрирование табличным способом и способом подстановки. Приложение интеграла: В результате изучения темы студент должен:Знать:- определение неопределенного и определенного интегралов; - формулы интегрирования с помощью замены переменной и интегрирования по частям внеопределенных и определенных интегралов;- формулы интегрирования Уметь: вычислять интегралы, находить площадь кривой трапеции. КОМИТЕТ ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖНОЙ ПОЛИТИКИ ВОЛГОГРАДСКОЙ ОБЛАСТИ государственное бюджетное профессиональное образовательное учреждение "Себряковский технологический техникум" (ГБПОУ "СТТ") Специальность: 08.02.09 Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий Контрольная работа по дисциплине: Математика вариант 3
г. Михайловка 2022 Вариант 1 Задание №1. Вычислите следующие пределы, не пользуясь правилом Лопиталя: а) 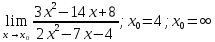 б) б)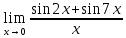 в) 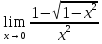 Задание №2. Решите систему по формулам Крамера : Задание №2. Решите систему по формулам Крамера :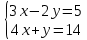 Задание №3. Найдите производные следующих функций: а) 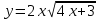 б) 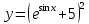 Задание №4.Решите задачу: Тело движется по прямой со скоростью 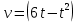 м/с. Вычислите путь, м/с. Вычислите путь,пройденный телом от начала движения до остановки. Задание №5. Даны комплексные числа: 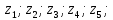 а) Вычислите: 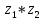 ; ;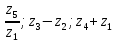 . .б) Представьте 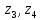 в тригонометрической форме. в тригонометрической форме.в) Запишите 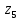 в показательной форме. в показательной форме. 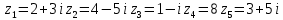 Задание №6. Найти математическое ожидание, дисперсию случайной величины X, если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. а) 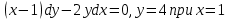 б) 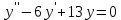 Вариант 2 Задание №1. Вычислите следующие пределы, не пользуясь правилом Лопиталя: a) 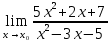 ; ;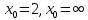 ; б) ; б) 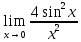 ; в) ; в) 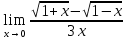 Задание N2.Решите систему по формулам Крамера : 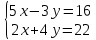 Задание №3. Найдите производные следующих функций: а) 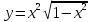 ; б) ; б)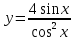 Задание №4. Решите задачу: Тело движется по прямой со скоростью 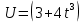 м/с. Вычислите путь, пройденный телом за 3-ю секунду. м/с. Вычислите путь, пройденный телом за 3-ю секунду. Задание №5. Даны комплексные числа: 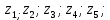 Вычислить: 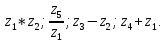 Представьте 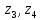 в тригонометрической форме. в тригонометрической форме. Запишите 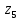 в показательной форме. в показательной форме.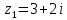 ; ; 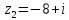 ; ;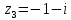 ; ; 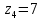 ; ; 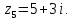 Задание №6. Найти математическое ожидание, дисперсию случайной величины. Х, если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частые решения, удовлетворяющие данным условиям. 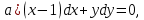 при y = 0 при x = 2. при y = 0 при x = 2. б) 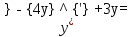 Вариант 3 Задание №1 Вычислите следующие пределы, не пользуясь правилом Лопиталя: а) 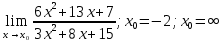 б) б)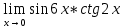 в) в)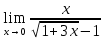 Задание №2.Решите систему по формулам Крамера : 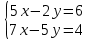 Задание №3 Найдите производные следующих функций: а) 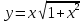 б) б)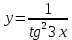 Задание №4Решите задачу: Тело движется прямолинейно со скоростью 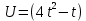 м/с. Вычислите путь, пройденный телом за 5 сек. м/с. Вычислите путь, пройденный телом за 5 сек.Задание №5 .Даны комплексные числа: 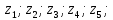 а) Вычислить: 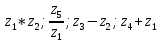 б) Представьте 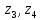 в тригонометрической форме. в тригонометрической форме.в) Запишите 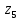 в показательной форме. в показательной форме.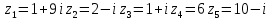 Задание №6 Найти математическое ожидание, дисперсию случайной величины X, если закон ее распределения задан таблицей.
Задание №7 Решите дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. а) 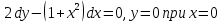 б) 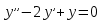 Вариант 4 Задание №1. Вычислите следующие пределы, не пользуясь правилом Лопиталя. 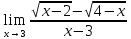 б) б)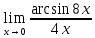 в) в)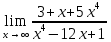 Задание №2.. Решите систему по формулам Крамера : 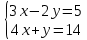 Задание №3.Найти производные следующих функций. 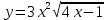 б) б)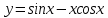 Задание №4. Решите задачу. Скорость точки задана уравнением 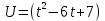 м/с. Найдитеуравнение движения, если к моменту начала отчета времени точка прошла путь S=4м м/с. Найдитеуравнение движения, если к моменту начала отчета времени точка прошла путь S=4мЗадание №5.Даны комплексные числа: 𝑧1; 𝑧2; 𝑧3; 𝑧4; 𝑧5; а) Вычислить: 𝑧1∗𝑧2; 𝑧5/𝑧1; 𝑧3−𝑧2; 𝑧4+𝑧1. б) Представьте 𝑧3, 𝑧4 в тригонометрической форме. в) Запишите 𝑧5 в показательной форме. 6) z1=1-9i 𝑧2=1-2i 𝑧3=1+i 𝑧4=5 𝑧5=1+10i Задание №6. Найти математическое ожидание, дисперсию случайной величины 𝑋, если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. 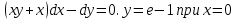 б) 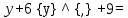 Вариант 5 Задание №1. а) 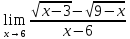 ;б) ;б) 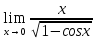 в) в)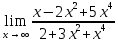 Задание №2.Решить систему уравнений по формулам Крамера: 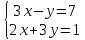 Задание №3.Найдите производные следующих функций. а) 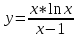 б) б) 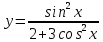 Задание №4.Скорость точки задана уравнением ʊ =4cost м/с.Найтиуравнение движения, если в момент t= 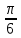 точка находиться на расстоянии S=8м от начала счета пути. точка находиться на расстоянии S=8м от начала счета пути.Задание №5.Даны комплексные числа: Z1;Z2;Z3;Z4;Z5; а)Вычислить: Z1+Z2; 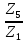 ;Z3-Z2; Z4+Z1 ;Z3-Z2; Z4+Z1б)Представьте Z3, Z4 в тригонометрической форме. в)Запишите Z5 в показательной форме. 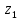 =3-2i =3-2i 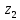 =1+8i =1+8i 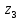 =-3+3i =-3+3i 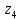 =4 =4 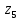 =2+2i =2+2iЗадание №6. Найти математическое ожидание, дисперсию случайной величины X, если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. 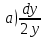 - dx = 0, y = 3 при x = 0 - dx = 0, y = 3 при x = 0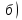 y'' + y'' + 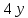 ' - 12y = 0 ' - 12y = 0Вариант 6 Задание №1. Вычислите следующие пределы, не пользуясь правилом Лопиталя: а) 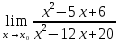 ; ;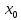 = 5, = 5, 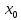 = = 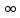 б) б) 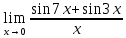 в) в)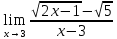 Задание №2. Решить систему уравнений по формулам Крамера: 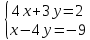 Задание №3Найдите производные следующих функций: а) 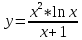 б) б) 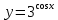 Задание 43.Решите задачу: Найти путь, пройденный телом от начала движения до остановки, если его скорость определяется по формуле 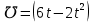 м/с. м/с.Задание №5.Даны комплексные числа: 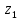 ; ; 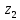 ; ; 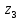 ; ; 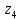 ; ; 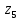 ; ;а) Вычислить: 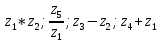 . .б) Представьте 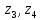 в тригонометрической форме. в тригонометрической форме.в) Запишите 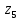 в показательной форме. в показательной форме.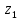 =9+i =9+i 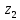 =-3-i =-3-i 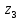 =3+3i =3+3i 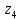 =3 =3 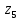 =2-2i =2-2iЗадание №6. Найти математическое ожидание, дисперсию случайной величины 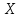 , если закон её распределения задан таблицей. , если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. 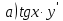 = = 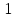 + + 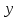 , , 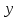 = = 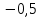 при при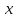 = = 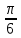 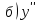 + + 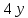 = 0 = 0Вариант 7 Задание №1.Вычислите следующие пределы, не пользуясь правилом Лопиталя: а) 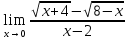 ;б) ;б) 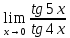 в) в)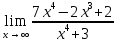 Задание №2..Решить систему уравнений по формулам Крамера: 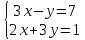 Задание №3.Найдите производные следующих функций. а) 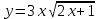 б) б) 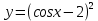 Задание №4. Скорость движение тела ʊ =(4t - 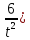 м/с. Определить его путь за 3 секунды м/с. Определить его путь за 3 секундыЗадание №5. Даны комплексные числа: Z1;Z2;Z3;Z4;Z5; а)Вычислить: Z1+Z2; 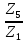 ;Z3-Z2; Z4+Z1 ;Z3-Z2; Z4+Z1б)Представьте Z3, Z4 в тригонометрической форме. в)Запишите Z5 в показательной форме. 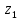 =7+2i =7+2i 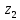 =3-i =3-i 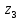 =-3-3i =-3-3i 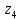 =2 =2 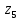 =-2+2i =-2+2iЗадание №6. Найти математическое ожидание, дисперсию случайной величины X, если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. 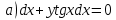 , y= 1 при x = 0 , y= 1 при x = 0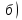 y'' - y'' - 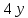 ' = 0 ' = 0Вариант 8 Задание №1.Вычислите следующие пределы, не пользуясь правилом Лопиталя: а) 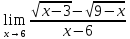 ;б) ;б) 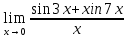 в) в)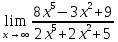 Задание №2.. Решите систему по формулам Крамера : 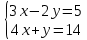 Задание №3.Найдите производные следующих функций. а) 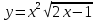 б) б) 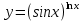 Задание №4. Скорость движения тела определяется по формуле ʊ = (3 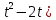 м/с. Какой путь тело пройдет за 5сек от начала движения. м/с. Какой путь тело пройдет за 5сек от начала движения.Задание №5. Даны комплексные числа: Z1;Z2;Z3;Z4;Z5; а)Вычислить: Z1+Z2; 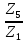 ;Z3-Z2; Z4+Z1 ;Z3-Z2; Z4+Z1б)Представьте Z3, Z4 в тригонометрической форме. в)Запишите Z5 в показательной форме. 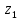 =6-4i =6-4i 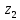 =-2+3i =-2+3i 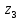 =3-3i =3-3i 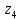 =1 =1 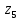 =-2-2i =-2-2iЗадание №6. Найти математическое ожидание, дисперсию случайной величины X, если закон её распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. 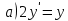 , y = 1 при x = 0 , y = 1 при x = 0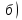 y'' + y'' + 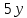 ' + 6y = 0 ' + 6y = 0Вариант №9. Задание №1. Вычислите следующие пределы, не пользуясь правилом Лопиталя: 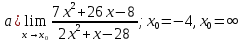 б) 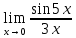 в) 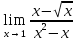 Задание №2.Решить систему уравнений по формулам Крамера: 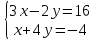 Задание №3. Найдите производные следующих функций: а) 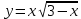 б) 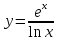 Задание №4. Решите задачу: Тело движется прямолинейно со скоростью U(t)=(4t+a) м/с. Найдите а, если известно, что путь, пройденный телом за 2 сек. от начала движения, равен 3м. Задание №5. Даны комплексные числа: 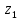 ; ;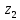 ; ;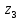 ; ;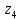 ; ;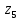 ; ;а)Вычислите 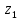 * *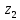 ; ;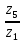 ; ;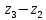 ; ;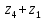 . .б)Представьте 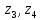 в тригонометрической форме. в тригонометрической форме.в)Запишите 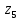 в показательной форме. в показательной форме.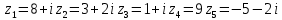 Задание №6.Найти математическое ожидание, дисперсию случайной величины X, если закон ее распределения задан таблицей.
Задание №7.Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. а) 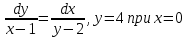 б) 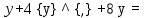 Вариант 10 Задание №1. Вычислите следующие пределы, не пользуясь правилом Лопиталя. 10) а) limx-x0 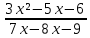 ; х0=3, х0=∞ б) limх-0 ; х0=3, х0=∞ б) limх-0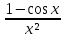 в)limх-7 в)limх-7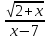 Задание №2. Решите систему по формулам Крамера : 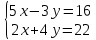 Задание №3.Найдите производные следующих функций: 10) а) у = х2 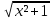 б) у = б) у = 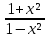 Задание №4. Решите задачу: 10) Тело движется прямолинейно со скоростью υ(t) = (2t3+1) м/с. Найдите путь, пройденный телом за промежуток времени от t=1c до t=3c. Задание №5. Даны комплексные числа: z1;z2;z3;z4;z5; а) Вычислить z1 - z2; 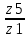 ; z3- z2; z4+ z1. ; z3- z2; z4+ z1.б) Представьте z3,z4 в тригонометрической форме. в) Запишите z5в показательной форме. 10) z1 = 2 - i z2 = 1+9i z3 = 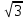 +i z4 = 5 z5 =12 – i +i z4 = 5 z5 =12 – iЗадание №6. Найдите математическое ожидание, дисперсию случайной величины Х, если закон ее распределения задан таблицей.
Задание №7. Решить дифференциальные уравнения и найти частные решения, удовлетворяющие данным условиям. 10) а) 4xydx = (x2+1)dy, y = 4 при х = 1 б) у″ + 6у′ + 9=0 |