Математика для заочной формы обучение. Методические указания и контрольные задания по дисциплине Математика и математическая статистика
 Скачать 104.25 Kb. Скачать 104.25 Kb.
|
|
Задание № 3 В задачах 31-40 вычислить неопределенные интегралы, результат проверить дифференцированием. 31. а)  ; б) ; б)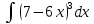 . .32. а)  ; б) ; б)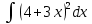 . .33. а) 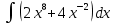 ; б) ; б)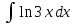 . .34. а) 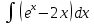 ; б) ; б)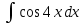 . .35. а) 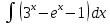 ; б) ; б)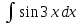 . .36. а) 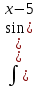 ; б) ; б)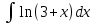 . .37. а) 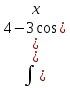 ; б) ; б)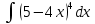 . .38. а) 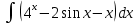 ; б) ; б)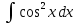 . .39. а) 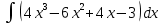 ; б) ; б)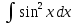 . .40. а) 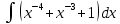 ; б) ; б)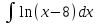 . .Решение типового примера 1) Найти неопределенные интегралы, результат проверить дифференцированием. 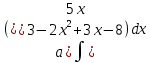 = = 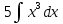 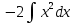 + + 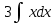  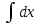 = = 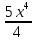 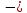 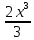 + + 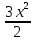 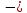 8x + C. 8x + C.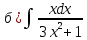 . .Сделаем замену переменной: x² = t. Тогда 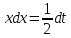 . Следовательно, . Следовательно,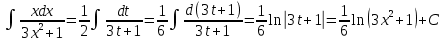 . .Задание № 5 В задачах 41-50 вычислить площадь фигуры, ограниченную заданными линиями: 41. у = х2, у = 49. 42. у = х3, у = 8. 43. у = х2+1, х = – 2, х = 2. 44. у = х2, у = 64. 45. у = х+2, х = 2, х = 4. 46. у = х3+1, у = 9. 47. у = х2+1, у = 9. 48. у = 2х, х = 1, х = 2. 49. у = х3+1, у = 28. 50. у = х2+2, у = 27 Решение типового примера. Вычислить площадь криволинейной трапеции, ограниченной линиями у = 4 - х² и у=0. 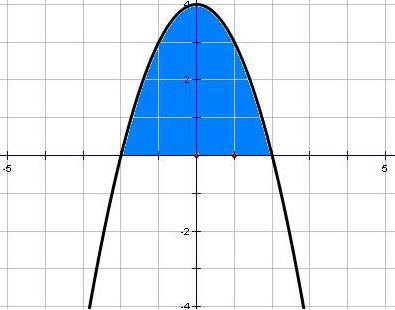 у = 4 – х²- квадратичная функция, график – парабола, ветви направлены вниз, вершина (0;4) у = 4 – х²- квадратичная функция, график – парабола, ветви направлены вниз, вершина (0;4) у= 0 - ось абсцисс. Найдём точки пересечения параболы с осью х: 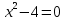 ; ; 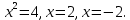 Найдем S = 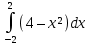 = =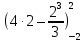 = – (4·(–2) – = – (4·(–2) – 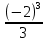 ) = ) =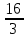 – (– – (–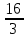 ) = ) = 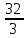 = =10 = =10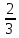 (кв.ед). (кв.ед). Ответ: 10 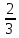 кв.ед. кв.ед. |
