Математика для заочной формы обучение. Методические указания и контрольные задания по дисциплине Математика и математическая статистика
 Скачать 104.25 Kb. Скачать 104.25 Kb.
|
|
Простейшие матричные уравнения и их решение. Пусть дана система уравнений  Рассмотрим матрицу, составленную из коэффициентов при неизвестных: А =  . .Свободные члены и неизвестные запишем в виде матриц-столбцов В = 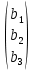 , X = , X =  . .Тогда матричным уравнением называется уравнение вида А·Х = В. План решения матричных уравнений: Найти обратную матрицу А–1 Найти произведение обратной матрицы А–1 на столбец свободных членов В, т.е. А–1·В Пользуясь определением равных матриц, записать ответ. Пример: Решить матричное уравнение 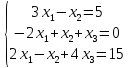 . .Составим матричное уравнение А·Х = В: А = 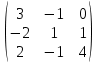 , X = , X =  , В = , В = 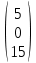 Найдем обратную матрицу А–1 Вычислим определитель D= 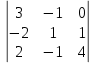 =3 =3  – (–1) – (–1) 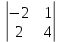 +0 +0 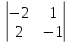 = 3·(4+1)+1·(– 8–2) =5 ≠0 = 3·(4+1)+1·(– 8–2) =5 ≠0Запишем все алгебраические дополнения: А11=(–1)1+1  = 5, А21=(–1)2+1 = 5, А21=(–1)2+1  = 4, А31=(–1)3+1 = 4, А31=(–1)3+1  = – 1, = – 1,А12=(–1)1+2 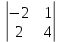 = 10, А22=(–1)2+2 = 10, А22=(–1)2+2 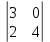 = 12, А32=(–1)3+2 = 12, А32=(–1)3+2 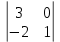 = – 3, = – 3,А13=(–1)1+3 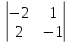 = 0, А23=(–1)2+3 = 0, А23=(–1)2+3 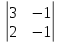 = 1, А33=(–1)3+3 = 1, А33=(–1)3+3 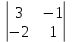 =5. =5.Запишем новую матрицу и транспонируем: А* = 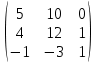 , АТ= , АТ= 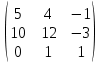 Запишем обратную матрицу: A-1 = 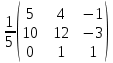 = = 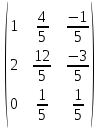 Х =  · ·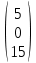 = = 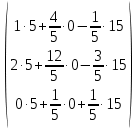 = = 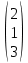 Итак, 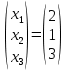 , т.е. х1=2, х2=1, х3=3. , т.е. х1=2, х2=1, х3=3.Решение систем линейных уравнений методом Крамера. Теорема: Система п уравнений с п неизвестными, определитель которой ≠ 0, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов. Пусть дана система линейных уравнений с неизвестными:  . .Из коэффициентов при неизвестных составим матрицу А, а из свободных членов – матрицу-столбец В, т.е. А =  , В = , В = 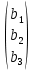 . .Если в определителе системы заменить столбцы коэффициентов при неизвестных на столбец свободных членов, то получим: Dх = 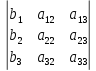 , Dу = , Dу = 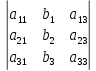 , Dz = , Dz = 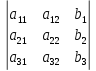 Тогда для решения системы запишется так: X= 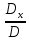 , У = , У = 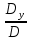 , Z = , Z = 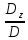 . .Пример: Решить систему уравнений 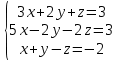 Составим матрицу из коэффициентов при неизвестных А =  и из свободных членов В = и из свободных членов В = 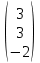 . .Вычислим определитель системы D= 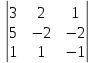 = 3 = 3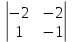 – 2 – 2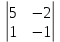 + 1 + 1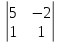 =25 ≠0 =25 ≠0Вычислим определители при неизвестных: Dх = 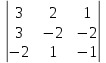 = 3 = 3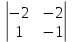 – 2 – 2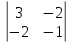 + 1 + 1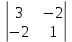 =25 =25Dу = 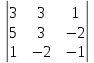 = 3 = 3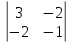 – 3 – 3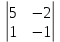 + 1 + 1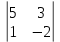 = – 25 = – 25Dz = 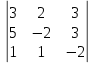 = 3 = 3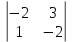 – 2 – 2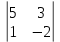 + 3 + 3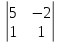 = 50 = 50Найдем значения X= 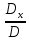 = = 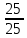 = 1, У = = 1, У = 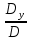 = =  = – 1, Z = = – 1, Z = 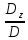 = =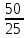 = 2. = 2.Ответ: (1; –1; 2) Решение систем линейных уравнений методом Гаусса. Суть метода - последовательное исключение неизвестных. С помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные. Пример 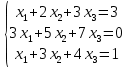 Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 3 × 4, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены. 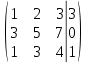 1. Проведём следующие действия: первую строку так и перепишем Из строки № 2 вычтем строку № 1 умноженную на 3 Из строки № 3 вычтем строку № 1. Получим:  2. Проведём следующие действия: Строку № 2 умножим на -1 Из строки № 3 вычтем строку № 2. Получим: 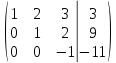 3. Проведѐм следующие действия: Строку № 3 умножим на -1 Из строки № 2 вычтем строку № 3 умноженную на 2 и запишем вторую строку Из строки № 1 вычтем строку № 3 умноженную на 3 и запишем первую строку. Получим: 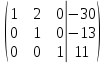 4. Проведѐм следующие действия: Из строки № 1 вычтем строку № 2 умноженную на 2. Получим: 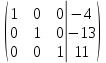 В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение: х1= –4, х2= –13, х3 = 11. Предел функции. Вычисление предела функции. Пусть f(x) и (x) – функции, для которых существуют пределы при x 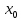 (x): (x): 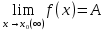 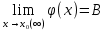 Сформулируем основные теоремы о пределах: Функция не может иметь более одного предела. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. 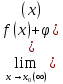 Предел произведения конечного числа функций равен произведению пределов этих функций, т.е. 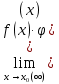 В частности, постоянный множитель можно выносить за знак предела, т.е. 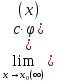 Предел частного двух функций равен частному пределов этих функций, т.е. 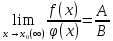 , , 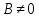 Правила раскрытия неопределенностей: 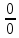 и и 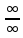 Правило раскрытия неопределенности 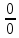 . Чтобы раскрыть неопределенность . Чтобы раскрыть неопределенность 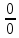 надо числитель и знаменатель дроби разложить на множители так, чтобы можно было сократить. надо числитель и знаменатель дроби разложить на множители так, чтобы можно было сократить.Правило раскрытия неопределенности 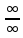 . Чтобы раскрыть . Чтобы раскрыть 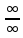 неопределенность надо числитель и знаменатель дроби сократить на самую большую степень х в знаменателе. неопределенность надо числитель и знаменатель дроби сократить на самую большую степень х в знаменателе.Определение производной функции Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение 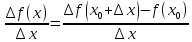 , при ∆х стремящемся к нулю. , при ∆х стремящемся к нулю.Основные правила дифференцирования (f + g) ' = f ' + g ' (f − g) ' = f ' − g ' (f · g) ' = f' ·g + g'·f 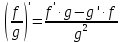 Формулы дифференцирования
Пример: Найти значение производной функции у = sin (4x – 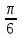 ) в точке х0 = ) в точке х0 = 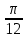 Найдем производную данной функции по правилу дифференцирования сложной функции: у′ = (sin (4x – 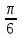 ))′ = (4x – ))′ = (4x – 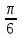 )′·cos(4x – )′·cos(4x – 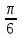 ) = 4 cos(4x – ) = 4 cos(4x – 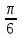 ) )у′ ( 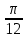 ) = 4 cos(4· ) = 4 cos(4·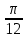 – – 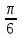 ) = 4 cos ) = 4 cos 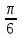 = 4· = 4·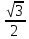 = 2 = 2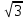 . Ответ: 2 . Ответ: 2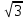 Пример: y = x3 – 3x2 + 5x + 2. Найти значение производной функции при y '(–1). Найдем производную данной функции: y ' = 3x2 – 6x+ 5. Следовательно, y'(–1) = 14. Ответ:14. Пример: Найти производную данной функцииy = ln x · cos x. Найдем производную данной функции по правилу дифференцирования: y ' = (ln x) ' cos x + ln x (cos x) ' =1/x∙cos x – ln x · sin x. Пример: Найти производную данной функцииy = 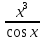 . .Найдем производную данной функции по правилу дифференцирования: y′ = 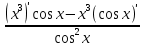 = = 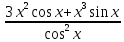 . . |

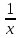 )'=
)'=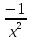
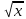 )'=
)'= 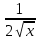
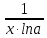
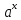 )'=
)'= 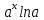
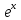 )'=
)'=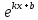 )'=
)'=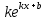
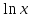 )'=
)'= 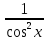

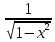
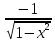
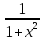
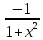
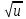 )'=
)'= 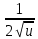 ·u′
·u′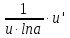
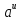 )'=
)'= 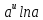 ·u′
·u′ )'=
)'=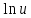 )'=
)'= 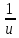 ·u′
·u′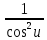 ·u′
·u′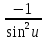 ·u′
·u′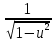 ·u′
·u′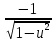 ·u′
·u′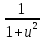 ·u′
·u′ ·u′
·u′