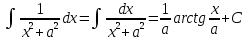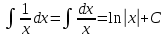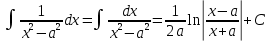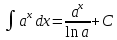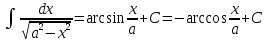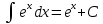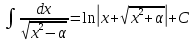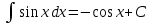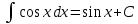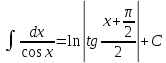Математика для заочной формы обучение. Методические указания и контрольные задания по дисциплине Математика и математическая статистика
 Скачать 104.25 Kb. Скачать 104.25 Kb.
|
|
Определение дифференциала функции С понятием производной тесно связано понятие дифференциала. Чтобы выяснить сущность этого понятия, рассмотрим функцию у =f(х), заданную в интервале (а, b) и имеющую в некоторой точке х этого интервала производную у' = f'΄(x). Придадим х приращение Δх, отличное от нуля, но не выводящее из интервала задания функции. Через Δy обозначим соответствующее приращение функции. Так как отношение 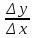 при стремлении Δх к нулю стремится к производной у', а разность между переменной, имеющей предел, и этим пределом есть величина бесконечно малая, то величина при стремлении Δх к нулю стремится к производной у', а разность между переменной, имеющей предел, и этим пределом есть величина бесконечно малая, то величина 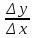 - у' стремится к нулю вместе с Δх. Предыдущее равенство можно записать в форме Δy= у' Δx+α Δx, где α – стремится к нулю вместе с Δх. - у' стремится к нулю вместе с Δх. Предыдущее равенство можно записать в форме Δy= у' Δx+α Δx, где α – стремится к нулю вместе с Δх.Обозначив αΔх = β , мы видим, что при бесконечно малом Δх переменная β также есть бесконечно малая величина и притом стремящаяся к нулю быстрее, чем Δх, так как 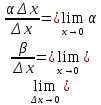 = 0. = 0.Таким образом, величина β есть бесконечно малая более высокого порядка, чем Δх. Это означает, что при весьма малых Δх величина β во много раз меньше, чем Δх. Доказательство этого факта имеется во многих руководствах по математическому анализу, но оно выходит за рамки нашей программы. Таким образом, при малых Δх величиной β = α Δх часто пренебрегают и довольствуются приближенной формулой Δy = f '(x) Δx. Определение. Дифференциалом или главной частью приращения функции у = f(х) в точке х, соответствующим приращению Δх, называется произведение производной f '(х), вычисленной в точке х, на Δх. Дифференциал функции у =f(х) обозначается через dy или df(x). Таким образом, dу = у 'Δх или df(x) =f '(х) Δх. Из определения дифференциала следует, что он является функцией двух независимых переменных – точки х и приращения Δх. Одним из основных свойств дифференциала, которое имеет широкое применение на практике – это то, что, пренебрегая бесконечно малыми более высокого порядка, можно приближенно заменять Δу – приращение функции ее дифференциалом dy. Определение первообразной функции Функция F(х) называется первообразной для функции f(х) на заданном промежутке, если для всех х из этого промежутка F/(х) = f(х). (Для краткости при нахождении первообразных промежуток на котором задана функция, обычно не указывается). Теорема: Если F(х) одна из первообразных для функции f(х) на заданном промежутке, то множество всех первообразных этой функции имеет вид: F(х) + С, где С – любое число. Для нахождения общего вида первообразной можно воспользоваться таблицей:
Примеры: Показать, что функция F(х) является первообразной функции f(х) на всей числовой прямой: а)F(х)= 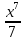 , f(х)=х6; б) F(х)=4х3-х+1, f(х)= 12х2-1. , f(х)=х6; б) F(х)=4х3-х+1, f(х)= 12х2-1.а) F’(х)= 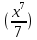 ’= ’=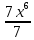 =х6=f(х). б) F’(х)= (4х3)’-х’+1’=12х2-1=f(х). =х6=f(х). б) F’(х)= (4х3)’-х’+1’=12х2-1=f(х).Найти одну из первообразных для функции f(х)= х12+3. Используя таблицу первообразных получим F(х)= 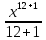 +3х+С= +3х+С= 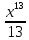 +3х+С. +3х+С.Для функции f(х)=х+5 найти такую первообразную, график которой проходит через точку А(2;5). Все первообразные функцииf(х)=х+5 находят по таблице F(х)= 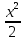 +5х+С. Найдем число С, такое, чтобы график функции проходил через точку А. Подставляя вместо х=2, F(х)=5, получаем 5= +5х+С. Найдем число С, такое, чтобы график функции проходил через точку А. Подставляя вместо х=2, F(х)=5, получаем 5= +5·2+С. Следовательно С= 5-14=-9. Значит F(х)= +5·2+С. Следовательно С= 5-14=-9. Значит F(х)=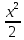 +5х-9. +5х-9.Определение неопределённого интеграла Пусть f(x) - функция, заданная на объединении интервалов вещественной оси. Набор всех первообразных для f(x) называется неопределённым интегралом от f(x) и обозначается ∫f(x)dx. Операция нахождения неопределённого интеграла по заданной функции f(x) называется интегрированием этой функции; найти неопределённый интеграл означает проинтегрировать данную функцию. Функцияf(x), записанная после знака интеграла (или, как часто говорят, под знаком интеграла), называется подынтегральной функцией. Согласно доказанным выше теоремам о виде первообразных, неопределённый интеграл от функции f(x) состоит из функций вида F(х)+С, где F(х) - какая-либо фиксированная первообразная для f(x), а С- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функцияf(x). Поэтому можно написать такую формулу: ∫f(x)dx=F(х)+С. Итак, для того чтобы доказать равенство ∫f(x)dx=F(х)+С, достаточно проверить, что F(х) - первообразная для f(x), то есть что F′(х)=f(x). Таблица неопределённых интегралов
Определение определённого интеграла Для вычисления определенных интегралов от непрерывных функций с конечными пределами необходимо, пользуясь известными методами интегрирования, получить первообразную от интегрируемой функции и, применяя формулу Ньютона-Лейбница  , найти разность значений первообразной при подстановке вместо переменной верхнего и нижнего пределов интегрирования. , найти разность значений первообразной при подстановке вместо переменной верхнего и нижнего пределов интегрирования.Задание № 1 Решение типовых примеров рассмотрено в теоретическом материале* В задачах 1-10 решить системы уравнений А) методом Крамера В) методом Гаусса Вариант 1 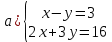 б) 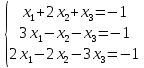 в) 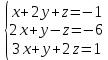 Вариант 2 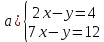 б) 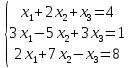 в) 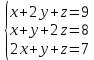 Вариант 3 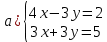 б) 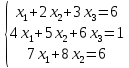 в)  Вариант 4 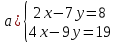 б) 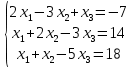 в) 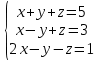 Вариант 5 a 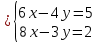 б) 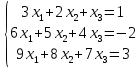 в) 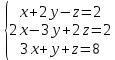 Вариант 6 a 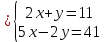 б) 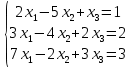 в)  Вариант 7 a 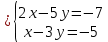 б) 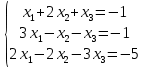 в) 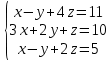 Вариант 8 a 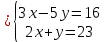 б) 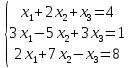 в) 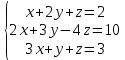 Вариант 9 a 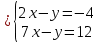 б) 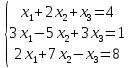 в) 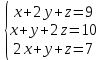 Вариант 10 a  б) 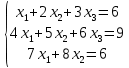 в)  Задание № 2 В задачах 11-20 вычислить пределы функции: 11. a) 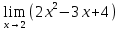 ; б) ; б) 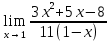 ; в) ; в) 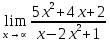 . .12. a) 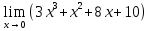 ; б) ; б) 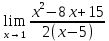 ; в) ; в) 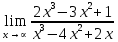 . .13. a) 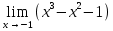 ; б) ; б) 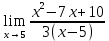 ; в) ; в) 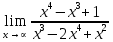 . .14. a) 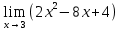 ; б) ; б) 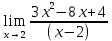 ; в) ; в) 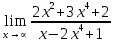 . .15. a) 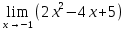 ; б) ; б) 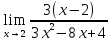 ; в) ; в) 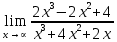 . .16. a) 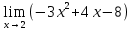 ; б) ; б) 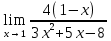 ; в) ; в) 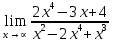 . .17. a) 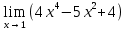 ; б) ; б) 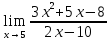 ; в) ; в) 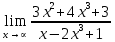 . .18. a) 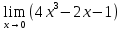 ; б) ; б) 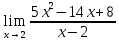 ; в) ; в) 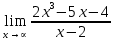 . .19. a) 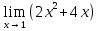 ; б) ; б) 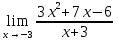 ; в) ; в) 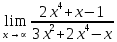 . .20. a) 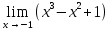 ; б) ; б) 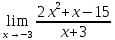 ; в) ; в) 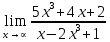 . .Решение типовых примеров Вычислить пределы: № 1. 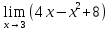 Для нахождения предела данной функции заменим аргумент х его предельным значением (выполним непосредственную подстановку): 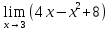 =4·3 – 32+8=12 – 9 + 8=11 =4·3 – 32+8=12 – 9 + 8=11№2. 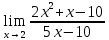 = = 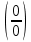 . .Непосредственная подстановка приводит к неопределенности типа 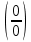 . .Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и до перехода к пределу сократим дробь на множитель х-2. Числитель – квадратный трехчлен разложим на множители: 2х2 + х – 10 = 0 D = (1)2 – 4·2· (– 10) = 1+80=81 (Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка) 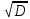 = = 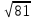 = 9 = 9x1 = 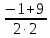 = = 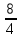 = 2. х2 = = 2. х2 = 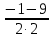 = = 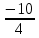 = = 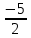 2х2 + х – 10 =2 (х-2)(х+ 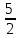 ) )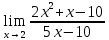 = = 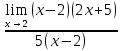 = =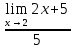 = = 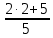 = = 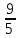 . Ответ: . Ответ: 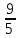 . .№2. 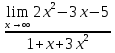 Сначала мы смотрим на числитель и находим х в старшей степени. Старшая степень в числителе равна двум. Теперь смотрим на знаменатель и тоже находим х в старшей степени. Старшая степень знаменателя равна двум. Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке. Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 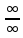 необходимо разделить числитель и знаменатель на хв старшей степени. необходимо разделить числитель и знаменатель на хв старшей степени.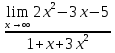 = = 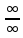 = (Разделим числитель и знаменатель на х2) = = (Разделим числитель и знаменатель на х2) = 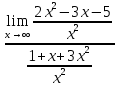 = = 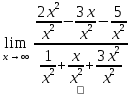 = = 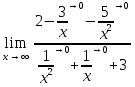 = = 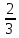 . Ответ: . Ответ: 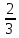 . . |

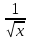
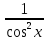
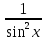
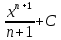
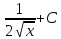

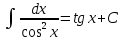
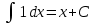
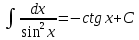
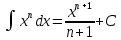 ,
, 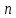 ≠ – 1
≠ – 1