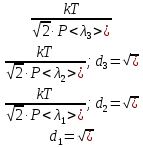Вопросы для самопроверки
Каковы условия возникновения внутреннего трения?
Что называется коэффициентом вязкости? Из формулы (2) вывести единицу измерения.
Что такое длина свободного пробега?
Как известно, воздух состоит из смеси газов. Что следует понимать под λ?
ЛАБОРАТОРНАЯ РАБОТА 5
Цель работы: опытным путем оценить порядок средней длины пробега молекул газа.
Приборы и принадлежности: установка на штативе для определения средней длины свободного пробега, мерная мензурка, стакан для слива воды, секундомер, термометр, барометр.
Теоретическое обоснование
Молекулярно-кинетическая теория позволила получить формулы, связывающие макропараметры газа (давление, объем, температура) с его микроскопическими параметрами (размеры и масса молекулы, скорость ее движения, средняя длина свободного пробега).
Пользуясь этими формулами, можно на основании измеренных макропараметров газа найти его микроскопические параметры. Для нахождения средней длины свободного пробега молекул газа 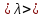 используют формулу, выражающую зависимость коэффициента внутреннего трения (вязкости) ηот используют формулу, выражающую зависимость коэффициента внутреннего трения (вязкости) ηот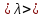 и и 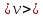 , ,
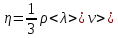 (1) (1)
где 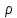 - плотность газа, - плотность газа, 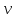 - средняя арифметическая скорость молекул газа. - средняя арифметическая скорость молекул газа.
Средняя арифметическая скорость по молекулярно-кинетической теории равна
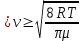 (2) (2)
где R- универсальная газовая постоянная, Т - абсолютная температура, 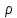 - масса одного моля газа. - масса одного моля газа.
Величины скоростей молекул в газах достаточно велики. Они достигают сотен метров в секунду. Но процесс переноса импульса происходит медленно. Причина этого в том, что в явлении переноса важную роль играют не только скорости молекул, но и столкновения между ними, которые препятствуют свободному движению молекул, заставляя их двигаться не прямолинейно, а зигзагообразно. Силы взаимодействия молекул становятся заметными при малых расстояниях между ними. Поэтому можно считать, что в газах на пути свободного пробега молекулы движутся прямолинейно и равномерно. Отклонение молекул от прямолинейных траекторий происходит только при достаточном сближении молекул. То минимальное расстояние между центрами двух молекул, на котором под действием сил отталкивания происходит явление, подобное удару, называется эффективным диаметром молекулы d. Расстояние, которое проходит молекула между двумя последовательными столкновениями, называют длиной свободного пробега молекул λ.
В связи с тем, что длины свободного пробега молекул несколько отличаются друг от друга, в расчетах используют среднюю длину свободного пробега молекул 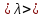 : :
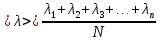
Зависимость между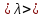 и dтакая: и dтакая:
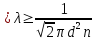 (3) (3)
где п - число молекул в единице объема газа.
Плотность газа 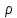 найдем из уравнения Менделеева-Клапейрона: найдем из уравнения Менделеева-Клапейрона:
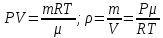 (4) (4)
где 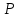 - давление газа. - давление газа.
Подставляя в выражение для коэффициента внутреннего трения (1) значения 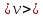 и и 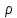 из формул (2) и (4), получим: из формул (2) и (4), получим:
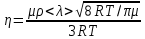 (5) (5)
В данной работе используется зависимость коэффициента вязкости 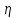 от параметров трубки С (рис. 7), через которую проходит газ, и разности давлений от параметров трубки С (рис. 7), через которую проходит газ, и разности давлений 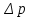 , возникающей на концах этой трубки. Эту зависимость выражают формулой Пуазейля: , возникающей на концах этой трубки. Эту зависимость выражают формулой Пуазейля:
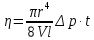 (6) (6)
где 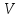 - объем газа (в данном случае воздуха, проходящего через трубку С длиной - объем газа (в данном случае воздуха, проходящего через трубку С длиной 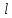 и радиусом и радиусом 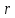 за время за время 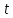 ; ; 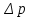 - разность давлений на концах трубки С. - разность давлений на концах трубки С.
Из формул (5) и (6) определяется средняя длина свободного пробега молекул газа:
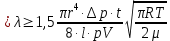 (7) (7)
В данной работе эта формула является расчетной для определения средней длины свободного пробега.
Эффективный диаметр молекул dможно вычислить по формуле (3), использовав для нахождения числа молекул в единице объема n основное уравнение молекулярно-кинетической теории газа в форме 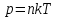 . .
Откуда
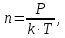 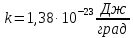 (8) (8)
Здесь 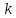 - постоянная Больцмана. Применив формулы (3) и (8), получаем выражение для эффективного диаметра молекул газа (9): - постоянная Больцмана. Применив формулы (3) и (8), получаем выражение для эффективного диаметра молекул газа (9):
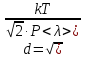 (9) (9)
где:
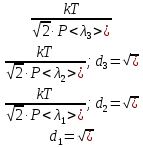
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.
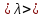 используют формулу, выражающую зависимость коэффициента внутреннего трения (вязкости) ηот
используют формулу, выражающую зависимость коэффициента внутреннего трения (вязкости) ηот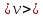 ,
,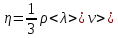 (1)
(1)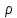 - плотность газа,
- плотность газа, 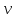 - средняя арифметическая скорость молекул газа.
- средняя арифметическая скорость молекул газа.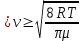 (2)
(2)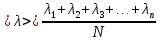
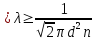 (3)
(3)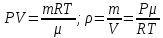 (4)
(4)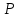 - давление газа.
- давление газа.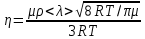 (5)
(5)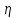 от параметров трубки С (рис. 7), через которую проходит газ, и разности давлений
от параметров трубки С (рис. 7), через которую проходит газ, и разности давлений 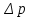 , возникающей на концах этой трубки. Эту зависимость выражают формулой Пуазейля:
, возникающей на концах этой трубки. Эту зависимость выражают формулой Пуазейля: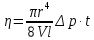 (6)
(6)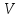 - объем газа (в данном случае воздуха, проходящего через трубку С длиной
- объем газа (в данном случае воздуха, проходящего через трубку С длиной 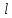 и радиусом
и радиусом 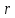 за время
за время 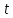 ;
; 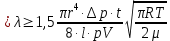 (7)
(7)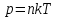 .
.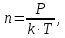
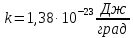 (8)
(8)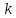 - постоянная Больцмана. Применив формулы (3) и (8), получаем выражение для эффективного диаметра молекул газа (9):
- постоянная Больцмана. Применив формулы (3) и (8), получаем выражение для эффективного диаметра молекул газа (9):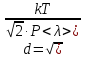 (9)
(9)