|
|
Физика молекулярная. Методические указания к лабораторным работам для студентов инженерных специальностей
Вопросы для самопроверки
Как формулируется первое начало термодинамики?
В чем состоит недостаточность первого начала термодинамики?
Сформулируйте физический смысл энтропии системы. Чему она равна и от чего зависит?
Установите связь между энтропией и вероятностью и выясните, как изменяется энтропия при обратимых процессах.
Какие процессы называют обратимыми и какие - необратимыми?
Как формулируется второе начало термодинамики?
ЛАБОРАТОРНАЯ РАБОТА 3 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА
ПО МЕТОДУ КЛЕМАНА-ДЕЗОРМА
Целью работы является ознакомление методом определения отношения теплоемкостей 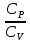 и определение отношения удельных теплоемкостей воздуха. и определение отношения удельных теплоемкостей воздуха.
Оборудование: прибор Клемана-Дезорма, насос Комовского. манометр.
Теоретическое введение
Тепловые свойства вещества характеризуются понятием теплоемкость. Теплоемкость как физическая величина определяется отношением количества теплоты, необходимой для нагрева, к величине изменения температуры вещества при нагреве: 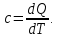
Величина теплоемкости газов зависит от условий их нагревания. Найдем эту зависимость, воспользовавшись уравнением состояния пологая для идеального газа 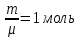 . .
Тогда уравнения Клайперона-Менделеева принимает вид:
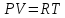 , (1) , (1)
Первое начало термодинамики запишем в виде:
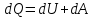
где 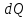 - количество тепла подводимого к термодинамической системе и затрачиваемое на увеличение ее внутренней энергии, - количество тепла подводимого к термодинамической системе и затрачиваемое на увеличение ее внутренней энергии, 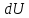 и на работу и на работу 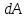 . совершаемую системой против внешних сил. . совершаемую системой против внешних сил.
По определению теплоемкости:
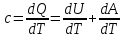 (2) (2)
Элементарная работа равна:
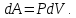
Рассмотрим два случая.
1. Газ нагревается при неизменном объеме. В этом случае 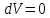 , и работа внешних сил равна нулю: , и работа внешних сил равна нулю:
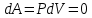
Все сообщаемое газу извне тепло идет на увеличение его внутренней энергии 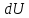 . Тогда из уравнения (2) следует, что удельная теплоемкость при постоянном объеме равна: . Тогда из уравнения (2) следует, что удельная теплоемкость при постоянном объеме равна:
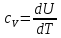 (3) (3)
2. Газ нагревается при постоянном давлении 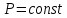 . В этом случае получаемое газом извне тепло идет не только на увеличение его внутренней энергии . В этом случае получаемое газом извне тепло идет не только на увеличение его внутренней энергии 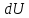 , но и на совершение газом работы , но и на совершение газом работы 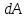 против внешней силы давления. Тогда удельная теплоемкость при постоянном давлении равна: против внешней силы давления. Тогда удельная теплоемкость при постоянном давлении равна:
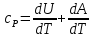 (4) (4)
Следовательно, для нагревания единицы массы газа на один градус при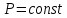 потребуется большое тепло, которое равно работе, совершаемой системой против внешней силы давления. Воспользовавшись уравнением состояния идеального газа (1) и взяв частную производную от параметров состояния потребуется большое тепло, которое равно работе, совершаемой системой против внешней силы давления. Воспользовавшись уравнением состояния идеального газа (1) и взяв частную производную от параметров состояния 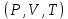 , получим: , получим:
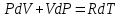 , (5) , (5)
но так как 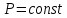 , то , то 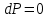 , и тогда: , и тогда:
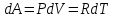
Подставляя эго выражение в (4) или заменяя через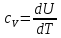 , получим: , получим:
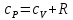 (6) (6)
Таким образом, теплоемкость 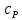 больше теплоемкости больше теплоемкости 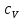 на величинутой работы на величинутой работы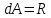 . которую совершает единица массы газа при расширении, происходящем при постоянном давлении в результате повышения его температуры на 1°. . которую совершает единица массы газа при расширении, происходящем при постоянном давлении в результате повышения его температуры на 1°.
Из двух удельных теплоемкостей можно непосредственно определить только 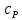 . Величина . Величина 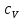 определяется косвенно. определяется косвенно.
Однако существуют способы непосредственного определения отношения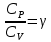 , которое зависит только от числа степеней свободы молекул газа. Это отношение входит в выражение закона Пуассона. , которое зависит только от числа степеней свободы молекул газа. Это отношение входит в выражение закона Пуассона.
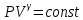 (7) описывающего адиабатический процесс в газах. (7) описывающего адиабатический процесс в газах.
Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой. Такой процесс будет происходить в системе, окруженной совершенно нетеплопроводными стенками. Так как совершенно нетеплопроводные стенки создать нельзя, то в действительности всякий процесс может лишь приближаться к адиабатическому. Если процесс протекает достаточно быстро, т.е. так, что система не успевает вступить в теплообмен с окружающей средой, то его можно считать адиабатическим и при отсутствии тепловой изоляции (например, при быстром сжатии и расширении газа).
Первое начало термодинамики для адиабатического процесса принимает вид:
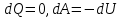 , ,
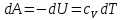 (8) (8)
Работа сжатия газа в адиабатическом процессе 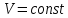 происходит только за счет изменения запаса его внутренней энергии. Поэтому адиабатическое расширение сопровождается понижением температуры, адиабатическое сжатие - ее повышением. происходит только за счет изменения запаса его внутренней энергии. Поэтому адиабатическое расширение сопровождается понижением температуры, адиабатическое сжатие - ее повышением.
|
|
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.
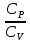 и определение отношения удельных теплоемкостей воздуха.
и определение отношения удельных теплоемкостей воздуха.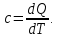
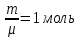 .
.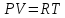 , (1)
, (1)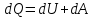
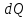 - количество тепла подводимого к термодинамической системе и затрачиваемое на увеличение ее внутренней энергии,
- количество тепла подводимого к термодинамической системе и затрачиваемое на увеличение ее внутренней энергии, 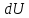 и на работу
и на работу 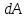 . совершаемую системой против внешних сил.
. совершаемую системой против внешних сил.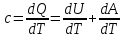 (2)
(2)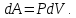
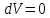 , и работа внешних сил равна нулю:
, и работа внешних сил равна нулю: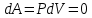
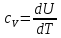 (3)
(3)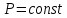 . В этом случае получаемое газом извне тепло идет не только на увеличение его внутренней энергии
. В этом случае получаемое газом извне тепло идет не только на увеличение его внутренней энергии 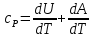 (4)
(4)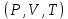 , получим:
, получим: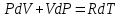 , (5)
, (5)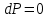 , и тогда:
, и тогда: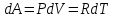
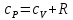 (6)
(6)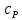 больше теплоемкости
больше теплоемкости 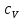 на величинутой работы
на величинутой работы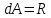 . которую совершает единица массы газа при расширении, происходящем при постоянном давлении в результате повышения его температуры на 1°.
. которую совершает единица массы газа при расширении, происходящем при постоянном давлении в результате повышения его температуры на 1°.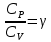 , которое зависит только от числа степеней свободы молекул газа. Это отношение входит в выражение закона Пуассона.
, которое зависит только от числа степеней свободы молекул газа. Это отношение входит в выражение закона Пуассона.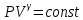 (7) описывающего адиабатический процесс в газах.
(7) описывающего адиабатический процесс в газах.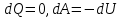 ,
,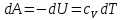 (8)
(8)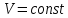 происходит только за счет изменения запаса его внутренней энергии. Поэтому адиабатическое расширение сопровождается понижением температуры, адиабатическое сжатие - ее повышением.
происходит только за счет изменения запаса его внутренней энергии. Поэтому адиабатическое расширение сопровождается понижением температуры, адиабатическое сжатие - ее повышением.