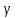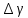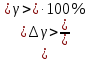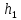Физика молекулярная. Методические указания к лабораторным работам для студентов инженерных специальностей
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Вопросы для самопроверкиПочему теплоемкость газа зависит от способов и условий нагревания? Что такое 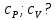 Почему Почему 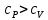 ? ?Какой процесс называется адиабатическим? Напишите уравнение Пуассона. Почему быстропротекающие процессы можно считать адиабатическими, и в какой мере справедливо? Таблица 3 - Значения показателя адиабаты
ЛАБОРАТОРНАЯ РАБОТА 4ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ И СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХАЦель работы: экспериментальное определение коэффициента внутреннего трения и длины свободного пробега молекул. Следует научиться применению закона Пуазейля для расчета коэффициента кинематической вязкости воздуха. Оборудование: аспиратор с водой, капилляр, осушительный фильтр с 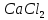 , манометр. , манометр.Теоретическое введениеЯвление внутреннего трения (вязкости) связано с возникновением сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по величине скоростями. Со стороны слоя, движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила. Наоборот, медленно перемещающийся слой тормозит быстро движущийся слой газа. Силы трения, которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев. С точки зрения кинетической теории газов причиной внутреннего трения является наложение упорядоченного движения слоев газа с различными скоростями 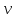 на хаотическое тепловое движение молекул, интенсивность которого зависит от температуры. Благодаря тепловому движению молекулы переходят из слоя В, движущегося со скоростью на хаотическое тепловое движение молекул, интенсивность которого зависит от температуры. Благодаря тепловому движению молекулы переходят из слоя В, движущегося со скоростью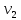 в слой А, движущийся со скоростью в слой А, движущийся со скоростью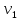 (рис.5.). (рис.5.).При этом молекулы из слоя В «переносят» в слой А импульсы 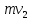 , своего упорядоченного движения. Если , своего упорядоченного движения. Если 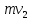 , то такие молекулы при столкновении с частицами слоя А ускоряют свое упорядоченное движение, а молекулы слоя А - замедляют. Наоборот, при переходе из быстро движущегося слоя А в слой В молекулы переносят импульсы , то такие молекулы при столкновении с частицами слоя А ускоряют свое упорядоченное движение, а молекулы слоя А - замедляют. Наоборот, при переходе из быстро движущегося слоя А в слой В молекулы переносят импульсы 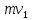 , и соударения между молекулами слоя В приводят к замедлению упорядоченного движения молекул слоя В. , и соударения между молекулами слоя В приводят к замедлению упорядоченного движения молекул слоя В.  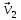 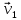 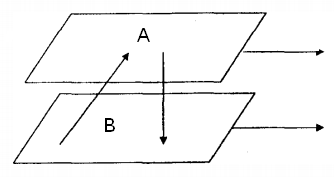 Рис. 5. Иллюстрация слоев жидкости Для явления внутреннего трения справедлив закон Ньютона: 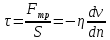 (1) (1)где 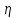 - коэффициент внутреннего трения, т.е. физическая величина, численно равная силе внутреннего трения, действующей на единицу площади поверхности слоя; - коэффициент внутреннего трения, т.е. физическая величина, численно равная силе внутреннего трения, действующей на единицу площади поверхности слоя; 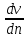 - изменение скорости движения слоев на единицу длины в направлении внутренней нормали к поверхности слоя - изменение скорости движения слоев на единицу длины в направлении внутренней нормали к поверхности слояЗнак «минус» в формуле (1) показывает, что сила внутреннего трения, действующая на рассматриваемую поверхность слоя, прямо противоположна по направлению производной вектора скорости движения 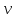 газа относительно нормали газа относительно нормали 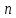 . .Величину 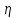 называют коэффициентом внутреннего трения, который численно равен силе трения к единице поверхности называют коэффициентом внутреннего трения, который численно равен силе трения к единице поверхности 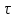 =1 напряжению трения при единичном градиенте скорости, т.е, =1 напряжению трения при единичном градиенте скорости, т.е, 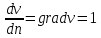 В международной системе единиц (СИ) 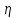 измеряется в измеряется в 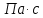 . Для определения . Для определения 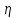 используется закон Пуазейля для ламинарного течения жидкости по капиллярам: используется закон Пуазейля для ламинарного течения жидкости по капиллярам: 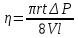 (2) (2)где 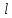 - длина капилляра, - длина капилляра, 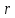 - радиус капилляра: - радиус капилляра: 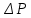 - разность давлений на концах трубки или капилляра; - разность давлений на концах трубки или капилляра; 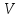 - объем газа или жидкости, прошедших за время t через капилляр. - объем газа или жидкости, прошедших за время t через капилляр.Коэффициент внутреннего трения согласно молекулярно-кинетической теории связан со средней длиной 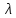 (это расстояние между двумя столкновениями молекулы свободного пробега молекул) соотношением: (это расстояние между двумя столкновениями молекулы свободного пробега молекул) соотношением: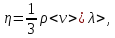 (3) (3)где 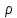 - плотность жидкости (газа) при данной температуре; - плотность жидкости (газа) при данной температуре;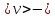 средняя арифметическая скорость молекул; средняя арифметическая скорость молекул; 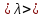 - средняя длина свободного пробега молекул. Известно, что: - средняя длина свободного пробега молекул. Известно, что: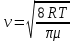 (4) (4)Согласно уравнению Клапейрона-Менделеева 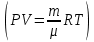 плотность газа равна: плотность газа равна: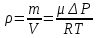 (5) (5)где 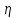 - молекулярный вес газа; - молекулярный вес газа; 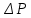 - разность давлений газа на концах трубкии капилляра, - разность давлений газа на концах трубкии капилляра, 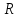 - универсальная газовая постоянная, - универсальная газовая постоянная, 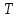 - абсолютная температура. - абсолютная температура.Из выражений (3), (4), (5) следует, что: 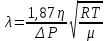 (6) (6) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||