|
|
Физика молекулярная. Методические указания к лабораторным работам для студентов инженерных специальностей
Вопросы для самопроверки
Сформулировать основные положения молекулярно-кинетической теории газов.
Что такое средняя длина свободного пробега молекул 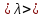 ? ?
Приведите вывод расчетной формулы для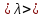 , используемой в данной работе. , используемой в данной работе.
Что такое эффективный диаметр молекул и как его вычисляют в данной работе?
Как выражается коэффициент вязкости через среднюю длину свободного пробега 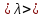 , и среднюю скорость молекул , и среднюю скорость молекул 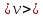 ? ?
ЛАБОРАТОРНАЯ РАБОТА 6 ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ЖИДКОСТИ
ПО МЕТОДУ ПАДАЮЩЕГО ШАРИКА
Целью работы является ознакомление с одним из методов определения коэффициента динамической вязкости жидкости - методом падающего шарика. В работе измеряется динамическая вязкость глицерина, а также изучаются причины возникновения силы внутреннего трения жидкости и методы ее вычисления.
Оборудование: стеклянный цилиндр с глицерином, металлические или свинцовые шарики, секундомер, линейка, микрометр.
Теоретическое введение
Всякая реальная жидкость обладает вязкостью, т.е. свойством оказывать сопротивление при перемещении одного слоя жидкости относительно другого.
При низких температурах (вблизи точки плавления) под действием приложенной внешней силы молекулы могут лишь немного смещаться относительно положения равновесия, испытывая действие упруговязких сил. Никакого скольжения слоев жидкости в этом случае не возникает.
Перемещение одного слоя жидкости относительно другого может происходить лишь тогда, когда молекулы получают возможность систематически изменять свое положение относительно других молекул. Таким образом, упруговязкие силы характеризуют сопротивление перемещению слоев жидкости под действием внешних сил.
При повышении температуры возрастает среднее расстояние между молекулами, увеличивается запас энергии молекул, жидкость становится как бы пористой, и при подходящих условиях молекулы проскакивают между раздвинувшимися соседними молекулами, то есть скачками переходят из одних

Рис. 8. Изображение движения молекул
временных положений равновесия в другие, выходя из окружения своих соседей - других молекул (рис. 8).
Обычно такие скачки происходят беспорядочным образом, однако, под действием разности давлений эти перескоки молекул принимают более направленный характер; молекулы чаще начинают перемещаться в сторону более низкого давления, начинается скольжение одного слоя по другому. Так как время между последовательными скачками молекул мало, то такое прерывное движение воспринимается как непрерывное скольжение.
Чем реже молекулы изменяют свои положения равновесия, тем менее текуча и более вязка жидкость.
Силы, действующие между скользящими друг относительно друга слоями жидкости, называются силами внутреннего трения, или силами вязкости. Эти силы направлены по касательной к поверхности слоев.
Рассмотрим однородную жидкость, заключенную между двумя параллельными поверхностями, скользящими друг относительно друга (рис. 9).
 
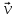
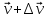
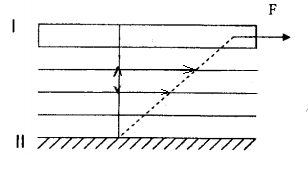
Рис. 9. Изменение скорости молекул слоев жидкости
Под действием внешней силы F поверхность I движется равномерно со скоростью 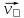 относительно неподвижной поверхности II. относительно неподвижной поверхности II.
Частицы жидкости, прилегающие непосредственно к поверхности I, прилипают к ней, образуя связанную с поверхностью тонкую пленку. Эта пленка полностью принимает участие в движении поверхности I со скоростью 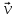 , но слой жидкости, прилегающий к этой пленке, отстает от последней, иточно так же каждый следующий слой жидкости, более отдаленный от поверхности I, отстает от слоев, более близких к поверхности I. Слои при этом скользят друг относительно друга, не перемешиваясь. Такое течение жидкости называется ламинарным (слоистым). , но слой жидкости, прилегающий к этой пленке, отстает от последней, иточно так же каждый следующий слой жидкости, более отдаленный от поверхности I, отстает от слоев, более близких к поверхности I. Слои при этом скользят друг относительно друга, не перемешиваясь. Такое течение жидкости называется ламинарным (слоистым).
Пусть два соседних слоя жидкости, расстояния между которыми dy, движутся со скоростями 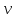 и и 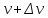 . Отношение . Отношение 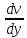 будет характеризовать изменение скорости в направлении оси у. Это отношение называется градиентом скорости. будет характеризовать изменение скорости в направлении оси у. Это отношение называется градиентом скорости.
Ньютоном было установлено, что сила внутреннего трения 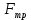 пропорциональна поверхности соприкасающихся слоев жидкости и градиенту скорости по направлению, перпендикулярному к направлению движения потока: пропорциональна поверхности соприкасающихся слоев жидкости и градиенту скорости по направлению, перпендикулярному к направлению движения потока:
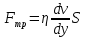 (1) (1)
Коэффициент пропорциональности 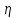 в формуле (1), характеризующий свойство данной жидкости, называется динамической вязкостью. Из формулы (1) имеем: в формуле (1), характеризующий свойство данной жидкости, называется динамической вязкостью. Из формулы (1) имеем:
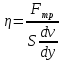 (2) (2)
Динамическая вязкость на основании формулы (2) численно равна силе внутреннего трения, действующей на единицу поверхности соприкасающихся слоев жидкости при градиенте скорости, равном единице. В системе СИ динамическая вязкость 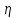 измеряется в измеряется в 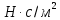 . .
Динамическая вязкость равна 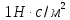 , если при градиенте скорости , если при градиенте скорости 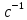 между двумя слоями жидкостями площадью 1 м2 действует сила внутреннего трения 1 Н. между двумя слоями жидкостями площадью 1 м2 действует сила внутреннего трения 1 Н.
В зависимости от рода жидкости и температуры динамическая вязкость 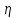 меняется в широких границах. меняется в широких границах.
Величина коэффициента динамической вязкости имеет большое значение при определении качества смазочных материалов, при расчете движения нефти и нефтепродуктов по трубопроводам, при расчете подачи топлива в двигателях внутреннего сгорания и в ряде других случаев.
В данной работе динамическая вязкость 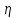 определяется по формуле Стокса: определяется по формуле Стокса:
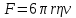 (3) (3)
Эта формула, полученная путем сложных преобразований из формулы (1), определяет величину силы внутреннего трения 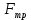 , действующую на шарик радиуса , действующую на шарик радиуса 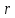 , движущийся с небольшой скоростью и в вязкой среде. , движущийся с небольшой скоростью и в вязкой среде.
Формула (3) справедлива при следующих условиях:
1) при малых скоростях движения;
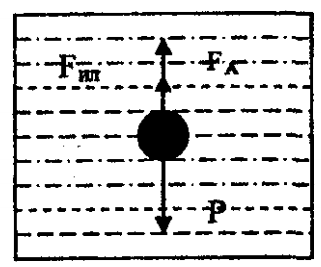
Рис. 10. Эпюра сил, действующих на тело, погруженное в жидкость
2) если среда, в которой движется шарик, практически безгранична, т.е. стенки сосуда находятся далеко от шарика.
Если считать, что сосуд, в котором движется шарик, имеет конечные размеры, то для случая, когда шарик падает вдоль оси цилиндрического сосуда радиусом R, сила внутреннего трения 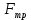 будет равна: будет равна:
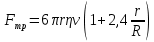 (4) (4)
Определим скорость, с которой движется шарик в вязкой среде, при условии, что сила вязкости определяется формулой Стокса (3). На шарик радиусом 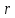 и плотностью и плотностью 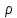 движущийся в вязкой среде, будут действовать следующие силы (рис. 10.). движущийся в вязкой среде, будут действовать следующие силы (рис. 10.).
сила тяжести:
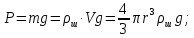 (5) (5)
сила вязкости:
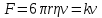 (6) (6)
где через 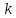 обозначен коэффициент при обозначен коэффициент при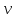 в формуле Стокса (3) в формуле Стокса (3)
выталкивающая сила, определяемая по закону Архимеда:
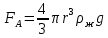 (7) (7)
где 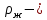 плотность жидкости, в которой движется шарик. плотность жидкости, в которой движется шарик.
Скорость движения шарика 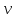 определим, интегрируя уравнение движения: определим, интегрируя уравнение движения:
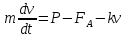 (8) (8)
Разделяя переменные, имеем:
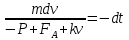
Интегрируя это уравнение, получаем:
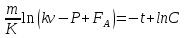
После потенционирования имеем:
k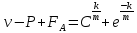
Произвольную постоянную интегрирования определяем из начальных условий:
при 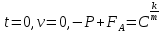
Отсюда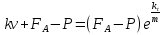 , тогда получим: , тогда получим:
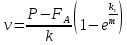 (9) (9)
Таким образом, скорость возрастает со временем по экспоненциальному закону, стремясь 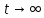 к некоторому предельному значению, которое мы обозначим через к некоторому предельному значению, которое мы обозначим через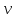 (установившаяся скорость). (установившаяся скорость).
Из формулы (9) следует, что:
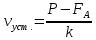 (10) (10)
Формулу (9) можно записать в виде:
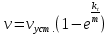 (11) (11)
График зависимости скорости от времени представлен на рис. 11
  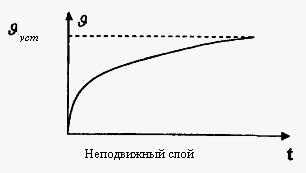
Рис. 11. Изменение скорости слоев жидкости относительно неподвижной поверхности
Таким образом, из формулы (11) следует, что чем больше вязкость и чем меньше радиус шарика, тем быстрее будет достигнуто предельное значение скорости 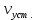 и движение шарика станет равномерным. и движение шарика станет равномерным.
Установившуюся скорость найдем, подставляя значения 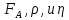 , из формул (5), (6), (7) в формулу (10): , из формул (5), (6), (7) в формулу (10):
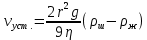 (12) (12)
Измеряя на опыте 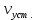 , ,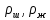 и подставляя измеренные значения в формулу (12), можно определить и подставляя измеренные значения в формулу (12), можно определить 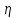 . .
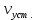 определяют по времени определяют по времени 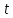 прохождения шарика между двумя метками, нанесенными на цилиндре, в котором он движется. Расстояние между метками прохождения шарика между двумя метками, нанесенными на цилиндре, в котором он движется. Расстояние между метками 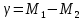 равно равно 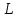 : :
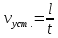 (13) (13)
Подставляя 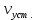 , в формулу (12) и заменяя в ней радиус шарика , в формулу (12) и заменяя в ней радиус шарика 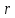 его диаметром его диаметром 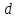 , получим расчетную формулу для определения , получим расчетную формулу для определения 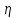 : :
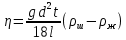 (14) (14)
которая и используется в данной работе.
|
|
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.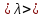 ?
?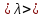 , используемой в данной работе.
, используемой в данной работе.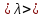 , и среднюю скорость молекул
, и среднюю скорость молекул 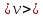 ?
?


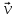
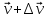

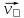 относительно неподвижной поверхности II.
относительно неподвижной поверхности II.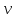 и
и 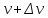 . Отношение
. Отношение 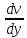 будет характеризовать изменение скорости в направлении оси у. Это отношение называется градиентом скорости.
будет характеризовать изменение скорости в направлении оси у. Это отношение называется градиентом скорости.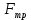 пропорциональна поверхности соприкасающихся слоев жидкости и градиенту скорости по направлению, перпендикулярному к направлению движения потока:
пропорциональна поверхности соприкасающихся слоев жидкости и градиенту скорости по направлению, перпендикулярному к направлению движения потока: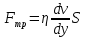 (1)
(1)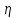 в формуле (1), характеризующий свойство данной жидкости, называется динамической вязкостью. Из формулы (1) имеем:
в формуле (1), характеризующий свойство данной жидкости, называется динамической вязкостью. Из формулы (1) имеем: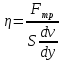 (2)
(2)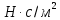 .
.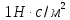 , если при градиенте скорости
, если при градиенте скорости 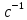 между двумя слоями жидкостями площадью 1 м2 действует сила внутреннего трения 1 Н.
между двумя слоями жидкостями площадью 1 м2 действует сила внутреннего трения 1 Н.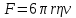 (3)
(3)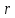 , движущийся с небольшой скоростью и в вязкой среде.
, движущийся с небольшой скоростью и в вязкой среде.
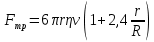 (4)
(4)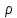 движущийся в вязкой среде, будут действовать следующие силы (рис. 10.).
движущийся в вязкой среде, будут действовать следующие силы (рис. 10.).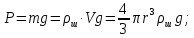 (5)
(5)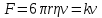 (6)
(6)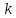 обозначен коэффициент при
обозначен коэффициент при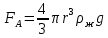 (7)
(7)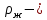 плотность жидкости, в которой движется шарик.
плотность жидкости, в которой движется шарик.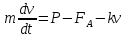 (8)
(8)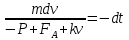
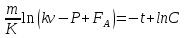
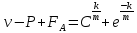
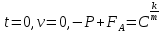
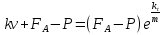 , тогда получим:
, тогда получим: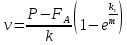 (9)
(9)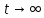 к некоторому предельному значению, которое мы обозначим через
к некоторому предельному значению, которое мы обозначим через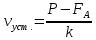 (10)
(10)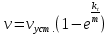 (11)
(11)


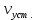 и движение шарика станет равномерным.
и движение шарика станет равномерным.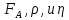 , из формул (5), (6), (7) в формулу (10):
, из формул (5), (6), (7) в формулу (10):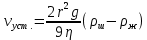 (12)
(12)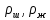 и подставляя измеренные значения в формулу (12), можно определить
и подставляя измеренные значения в формулу (12), можно определить 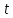 прохождения шарика между двумя метками, нанесенными на цилиндре, в котором он движется. Расстояние между метками
прохождения шарика между двумя метками, нанесенными на цилиндре, в котором он движется. Расстояние между метками 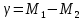 равно
равно 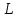 :
: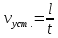 (13)
(13)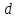 , получим расчетную формулу для определения
, получим расчетную формулу для определения 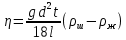 (14)
(14)