Методические указания к практическим работам по дисциплине б 16 Инженерная геодезия для направления 08. 03. 01 Строительство
 Скачать 385.78 Kb. Скачать 385.78 Kb.
|
1.2. Основные формулы оценки точности равноточных измерений1. Вероятнейшее значение измеряемой величины – арифметическая средина: хо = 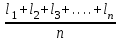 = [ l ] / n , = [ l ] / n ,где l – результат измерения; n – количество изерений. 2. Средняя истинная погрешность: θ = 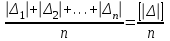 , ,где Δ = li – X – случайная истинная погрешность данного ряда измерений, li – результат измерения; X – истинная величина измерения. 3. Средняя квадратическая погрешность (СКП): - при наличии случайных истинных погрешностей (формула Гаусса) m² = 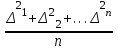 или m = или m = 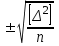 ; ;- при наличии случайных вероятнейших погрешностей (формула Бесселя) m = 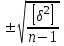 , , где δi = li – хо - вероятнейшая погрешность данного ряда измерений, хо – арифметическая средина, li – результат измерения. - по разностям двойных измерений m = 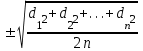 = = 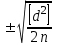 , ,где di = li – li’ - разность между первым и вторым результатами измерений одной и той же величины при отсутствии в ней систематической погрешности; m = 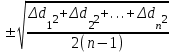 = = 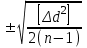 , ,где Δdi = di – d0 - разность между первым и вторым результатами измерений одной и той же величины и исключенной из нее систематической погрешности , которая вычисляется по формуле среднего арифметического: d0 = [d] / n. 4. Предельная погрешность : Δlпр = ±3m или Δlпр = ±2 m (при повышенных требованиях к точности измерений). 5. Средняя квадратическая погрешность арифметической средины: 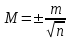 при n измерениях, при n измерениях, 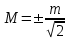 при двойных измерениях. при двойных измерениях.6. Средняя квадратическая погрешность функций: Вид фунции СКП а) Z = 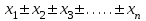 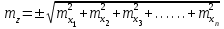 б) z = 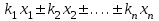 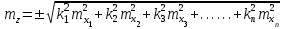 в) z = f (x1,x2, …xn) -функция 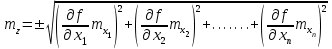 общего вида 1.3. Основные формулы оценки точности неравноточных измерений1. Вероятнейшее значение измеряемой величины – общая арифметическая средина: х0 = 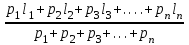 = [pl ] / [p] , = [pl ] / [p] ,где l – результат измерения; p – вес соответствующего результата измерения. 2. Средняя квадратическая погрешность результата измерения с весом, равным единице: а) 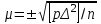 , где Δ – истинная погрешность измерения, р – вес данного измерения, n – количество измерений; , где Δ – истинная погрешность измерения, р – вес данного измерения, n – количество измерений;б) 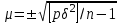 , где δ – вероятнейшая погрешность измерения; , где δ – вероятнейшая погрешность измерения;в) 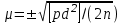 , где d - разность двойных измерений при отсутствии систематических погрешностей; , где d - разность двойных измерений при отсутствии систематических погрешностей;г) μ = 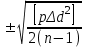 , где Δd – разность двойных измерений при исключении из нее систематической погрешности. , где Δd – разность двойных измерений при исключении из нее систематической погрешности.3. Средняя квадратическая погрешность общей арифметической средины: 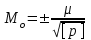 , , где [p] – сумма весов данного ряда измерений. 4. Средняя квадратическая погрешность результата измерений с весом p: 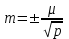 5. Веса функций измеренных величин: Вид фунции Вес функции а) Z = 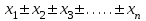 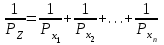 б) z = 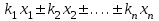 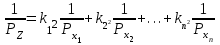 в) z = f (x1,x2, …xn) -функция 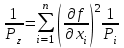 общего вида |
