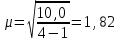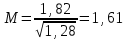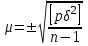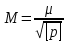Методические указания к практическим работам по дисциплине б 16 Инженерная геодезия для направления 08. 03. 01 Строительство
 Скачать 385.78 Kb. Скачать 385.78 Kb.
|
1.4. ЗаданияЗадание 1. Действия с приближенными числами Задания выполнить в соответствии с исходными данными по варианту и правилами действий с приближенными числами (см. Приложения).
1.1. Округлить число N до n значащих цифр и число N1 до n1 знаков после запятой: N = , N1 = 1.2. Определить сумму чисел N и N1 : N + N1 = 1.3. Вычислить произведение чисел N2 и N3, частное от деления этих чисел: N2 * N3 = N2 / N3 = 1.4. Возвести в n3 степень число N4 и извлечь корень квадратный из числа N5: 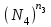 = = 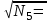 Задание 2. Оценка погрешности одного двойного измерения Определить абсолютную погрешность ΔD (расхождение значений), среднее значение Dср, относительную погрешность fотн двойного измерения линии (в прямом и обратном направлениях). Относительную погрешность записать в виде аликвотной дроби, то есть в виде 1/n , где n - натуральное число. Ответить на вопрос: «Допустимо ли полученное расхождение между двумя измерениями?». Допустимая относительная погрешность не должна превышать для: местности 1 категории (благоприятные условия измерений) - 1/2000; местности 2 категории (средние условия) - 1/1500 местности 3 категории (неблагоприятные условия измерений) - 1/1000. Исходные данные по варианту: Категория местности - Dпр = Dобр = Dср = ΔD= fотн = Задание 3. Обработка ряда истинных погрешностей измерений Истинная погрешность измерений может включать в себя не только случайную погрешность, но и систематическую, либо ряд систематических погрешностей. Если систематическая погрешность постоянно или односторонне действует на результаты многократных измерений, она исключается введением соответствующих поправок. На практике это не всегда удается сделать, поскольку на результат измерений могут влиять одновременно несколько систематических погрешностей, значение которых определить невозможно. В этом случае оценивается их совместное влияние как среднее арифметическое для ряда истинных погрешностей: θ 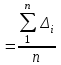 , где n - число измерений (погрешностей), , где n - число измерений (погрешностей), Δi– истинная погрешность измерения i . При значении θ («тета»),близком к нулю (сопоставимом с точностью измерений) делается вывод о незначительном влиянии систематической составляющей или ее отсутствии. В противном случае необходимо исключить систематическую погрешность вычитанием величины θ из величин истинных погрешностей Δi. После исключения систематической части остается случайная составляющая погрешности η (читается «эта»). ηi = Δi - θ. 2.1. Вычислить систематическую часть погрешности измерений θ, исключить ее из приведенных в таблице значений Δ. В заданном ряде из 24 измерений использовать по варианту значения истинных погрешностей для измерений №№ 7,8,15,16,23,24, которые даны в приложении. θ = 2.2. Определить среднюю квадратическую погрешность измерений mпосле исключения систематической составляющей, применив формулу Гаусса (см. методические указания). В формуле Гаусса нужно заменить величину Δ случайной составляющей η. Результат округлить до двух десятичных знаков. Ниже записать формулу Гаусса и вычисленное значение средней квадратической погрешности m: m = Результаты вычислений оформить в табличной форме:
В геодезических расчетах знак суммы часто обозначают квадратными скобками [ ]. Задание 4. Обработка ряда равноточных измерений с применением формулы Бесселя В соответствии с вариантом в приложении обработать результаты равноточных измерений угла наклона (число измерений n = 5): 3.1. Вычислить вероятнейшее значение измеренной величины (среднее арифметическое) - хo . Для упрощения вычислений использовать способ «ложного нуля». Для этого наименьшее значение принимают за начало отсчета и вычисляют отклонения от наименьшего значения ε = хi - хmin. Затем определяют вероятнейшее значение: хo = хmin + [ε] / n , где [ε] - сумма отклонений от наименьшего. 3.2. Вычислить среднюю квадратическую погрешность измерения - m ; В таблице буквой δ обозначена вероятнейшая погрешность хi - хo (за истинное значение принято среднее арифметическое значение измеренной величины). Записать и использовать формулу Бесселя: m = 3.3. Оценить точность определения среднего арифметического значения вычислением его средней квадратической погрешности М.
xmin= [ε]= [ε]/n= [δ]= [δ2]= xo= Задание 5. Оценка точности двойных равноточных измерений С применением нивелира измерено шесть превышений по черным ( h ) и красным ( h' ) сторонам реек. Результаты измерений в виде статисти-ческого ряда двойных равноточных измерений сведены в таблицу. По этим данным вычислить среднеквадратическую погрешность mh измерения превышения на станции по односторонним отсчетам, то есть каждого превышения.
[d] = [d2] = mh = Задание 6. Определение среднеквадратической погрешности функции измеренных величин Задание 6.1. Вычислить площадь S прямоугольного участка на местности со сторонами а = 30,15 м и b = 40,09 м, а также и ее СКП, если размеры участка получены рулеткой с относительной погрешностью 1/1500. S = ab = Записать выражение в общем виде для СКП:  ms = ± √(dS/da)2*(ma)2+(dS/db)2*(mb)2 ms = ± √(dS/da)2*(ma)2+(dS/db)2*(mb)2 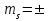 Вычислить частные производные по аргументу а и аргументу b: 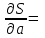 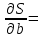 Вычислить СКП аргумента а и СКП аргумента b , используя понятие относительной погрешности: 1/N = 1/1500=ma / a; 1/N= 1/1500 = mb / b . ma= mb = Подставить числовые данные в выражение для ms – средней квадратической погрешности измеренной площади прямоугольника: ms = ± √ Записать результат вычислений в виде: S = a*b ± ms = Задание 6.2 При определении высоты объекта Н теодолитом были измерены углы наклона на верхнюю и нижнюю точку сооружения υв = +25о и υн = -5о10' cо средней квадратической погрешностью ± 0,2’, а также измерено расстояние до сооружения d = 70м с относительной погрешностью 1/5000. Определить высоту объекта и ее СКП.  h1 H υв d υн h2 При вычислениях нужно использовать формулы тригонометрического нивелирования: Н = h1+ h2 = d tg υв + d tg υн. Для первого и второго слагаемого в формуле Н получено выражение квадрата погрешности, которое следует поочередно применить к расчету: 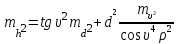 , где , где ρ´ = 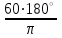 = ; mυ = , md = = ; mυ = , md = mh = mh1 + mh2 = Задание 7. Обработка неравноточных измерений Обработать результаты определения высоты точки, полученной по четырем ходам. Для определении весов отметок разных нивелирных ходов принимают вес каждого из результатов обратно пропорционально количеству превышений (штативов, станций) либо обратно пропорционально длине хода. В данной задаче для каждого хода рекомендуется принять вес рi = 1 / ni , где ni – число превышений в ходе. По примеру обработанной ведомости в соответствии с вариантом, дающим числа превышений в ходе, выполнить соответствующие вычисления. Использовать формулы, приведенные в приложении. При расчете среднего весового использовать «ложный нуль». Пример обработки:
=………………- средняя квадратическая погрешность весового среднего (мм) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||