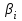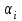Методические указания к практическим работам по дисциплине б 16 Инженерная геодезия для направления 08. 03. 01 Строительство
 Скачать 385.78 Kb. Скачать 385.78 Kb.
|
|
Бланки таблиц 1 и 2, а также бланк ведомости к вычислению координат для заполнения рекомендуется распечатать из заданий в ИОС. Путь в ИОСе: Учебные материалы – Контрольные материалы – Задания. Задание 3. Вычисление координат точек теодолитного хода Обработку теодолитного хода производят в специальной ведомости (таблица 5), в которую записывают значения измеренных углов (βизм), гори-зонтальные проложения линий (d), дирекционный угол одной из сторон полигона ( I-II) и координаты исходной точки (ХI и УI). Значения исходного дирекционного угла I-II и координат первой точки полигона ХI и УI студент выбирает по варианту из таблицы 4. Номер варианта соответствует последней цифре номера зачетки для исходных координат (для варианта №10 последняя цифра - 0). Исходный дирекционный угол принимается по последней цифре номера зачетки и по начальной букве фамилии студента. В таблице 3 приведен пример заполнения ведомости. Последовательность вычислений Увязка (уравнивание) угловых измерений Значения углов из графы 2 (табл. 3) суммируются: Σβизм. Вычисляется теоретическая сумма углов: Σβтеор = 180° ∙ (n - 2) , где n – количество измеренных углов. Определяется фактическая угловая невязка fβ = Σβизм - Σβтеор и невязка допустимая по формуле f βдоп = 2t 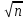 , где t – погрешность угловых измерений. В данной работе значение t = 0,5´. Если ошибка не превышает допустимую, то выполняют увязку углов. , где t – погрешность угловых измерений. В данной работе значение t = 0,5´. Если ошибка не превышает допустимую, то выполняют увязку углов.Увязка углов состоит в определении поправок в исходные данные и получении исправленных значений, сумма которых должна быть равна теоретической сумме углов. Считая, что каждый угол измерялся с одинаковой погрешностью, угловая невязка распределяется поровну на все углы с обратным знаком. Если теодолитный ход короткий, допустимо поправки вводить с таким расчетом, чтобы исправленные углы были округлены до целых минут. Сумма поправок должна равняться угловой невязке с обратным знаком. Пример: Σβизм = 540°1,1 Σβ теор = 180° ∙ (5 - 2) = 540° f β = 540°1,1' - 540° = 1,1' f β доп = 1' ∙ 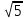 = 2,23' = 2,23' Так как угловая невязка (fβ) не превышает допустимую, можно приступить к увязке углов.Угловая невязка (f β) распределяется поровну на все углы с обратным знаком: 1,1'/5 = 0,22'. Так как запись углов в примере производится с точностью до 0,1', округляем поправки до 0,2' и 0,3', чтобы их сумма равнялась 1,1'. Записываем поправки с обратным знаком в графу 3. Поправки суммируются с учетом знака с соответствующими измерен-ными углами (βизм). Исправленные углы (βиспр) записываются в графу 4. Вычисление дирекционных углов сторон полигона и соответствующих румбов Дирекционные углы всех сторон полигона вычисляют по исходному значению I-II и исправленным значениям внутренних углов полигона. Значение дирекционного угла исходного направления I-II выбирается из таблицы 4 в зависимости от номера варианта и начальной буквы фамилии студента. Все последующие дирекционные углы вычисляют по правилу: дирекционный угол последующей стороны хода равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный горизонтальный угол β, лежащий справа по ходу: посл = пред + 180° - βисп Контролируются вычисления условием: вычисленный в конце расчета I- II должен быть равен исходному значению. Пример вычисления дирекционных углов: II- III = I-II + 180° - β2 = 112°00' + 180° - 89°08' = 202°52' III- IV = II- III + 180° - β3 = 202°52' + 180° - 156°22,4' = 226°29,6' IV- V = III- IV + 180°- β4 = 226°29,6' + 180° - 72°09,4' = 334°20,2' V- I = IV- V + 180° - β5 = 334°20,2' + 180° - 137°27,7' = 16°52,5' I- II = V- I + 180° - β1 = 16°52,5' + 180° - 84°52,5' = 112°00'. Вычисленные значения записываем в графу 5 (табл.3). В целях упрощения вычислений от дирекционных углов переходят к румбам по формулам: в I четверти (СВ) r = ; во II четверти (ЮВ) r = 180°- ; в III четверти (ЮЗ) r = - 180°; в IV четверти r = 360°- . Румбы записывают в графе 6 таблицы 3. Пример: Для I-II = 112°00' во II четверти r I-II = 180° - I-II = 180° - 112°00' = ЮВ: 68°00' ; для II-III = 202°52' в III четверти r II-III = II-III - 180° = 202°52' - 180° = ЮЗ: 22°52' для III-IV = 226°29,6' в III четверти r III-IV = III-IV - 180° = 226°29,6' - 180° = ЮЗ: 46°29,6' для IV-V = 334°20,2' в IV четверти r IV-V = 360° - IV-V = 360° - 334°20,2' = СЗ: 25°39,8' для V-I = 16°52,5' в I четверти r V-I = V-I = СВ: 16°52,5' Вычисление приращений координат Приращения координат находят по формулам прямой геодезической задачи с использованием микрокалькуляторов или четырехзначных математических таблиц тригонометрических функций: ∆x = ± d∙cos r, ∆y = ± d∙ sin r. Знак приращения координат зависит от знака косинуса или синуса дирекционного угла направления или от названия четверти прямоугольной системы координат (если для вычислений используются румбы).
Приращения координат можно вычислять не через румбы, а непосредственно через дирекционные углы (при этом знаки приращений координат появляются автоматически на дисплее калькулятора или компьютера): ∆x = d∙cos α, ∆y = d∙ sin α. В этом случае румбы не вычисляются, и в ведомости координат нет соответствующей графы. Контроль: теоретически алгебраическая сумма приращений в замкнутом полигоне (Σ∆x и Σ∆y) должна равняться нулю. Практически эти суммы отличаются от нуля, поэтому и возникают линейные невязки (f∆x и f∆y). Общая абсолютная погрешность (невязка) (fs) вычисляется по формуле: fs= 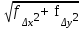 Относительная погрешность (fотн) вычисляется по формуле: fотн = 1/(Р : fs), где Р – периметр полигона. Относительную погрешность (fотн) сравнивают с допустимой (fдоп), которая равной 1/1000, 1/1500 или 1/2000 в зависимости от условий измерений. Если относительная погрешность не превышает допустимую (fдоп ≥ fотн), то выполняют увязку вычисленных приращений координат. Далее вычисляются приращения координат, которые записывают в графы 8 и 9 (табл.3). Пример: ∆x I- II = d I ∙ cos r = 113,70 ∙ cos 68°00' = 42,59 м ; ∆y I- II = d I ∙ sin r = 113,70 ∙ sin 68°00' = 105,42м Сумма положительных приращений ∆x составляет Σ+=202,38, а отрицательных Σ- =202,83. Их алгебраическая сумма дает линейную невязку f∆x = - 0,45 м. Сумма положительных приращений всех ∆y составляет Σ+= 140,37, отрицательных равна Σ- = 140,55. Их сумма дает линейную невязку f∆y = - 0,18 м Вычисляем абсолютную невязку (fs) и относительную невязку (fотн): fs = 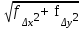 = =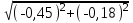 = = 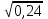 = 0,49м.; = 0,49м.; fотн = 1/(Р : fs) = 1/(522,78: 0,49) ≈ 1 / 1067 В данном примере относительная невязка не превышает допустимую невязку, то есть 1/1067 < 1/1000, поэтому можно увязывать вычисленные приращения координат. Увязка приращений координат Поправки в вычисленные приращения координат определяют по формулам: Х = 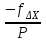 d , У = d , У =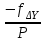 d. Вычисленная поправка округляется до 0,01 м. d. Вычисленная поправка округляется до 0,01 м. Контроль этого этапа работы: сумма поправок должна быть равна невязке с обратным знаком. Пример: Х I = 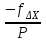  ∙ d I = - ∙ d I = - 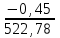 ∙ 113,7 = + 0,10м ; ∙ 113,7 = + 0,10м ; YI = 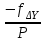 ∙ d I = - ∙ d I = -  ∙ 113,7 = + 0,04м ∙ 113,7 = + 0,04мВычисленные поправки записывают в графы 8 и 9 над приращениями координат (табл. 3). Поправки Х и У суммируются с соответствующими приращениями ∆x и ∆y, учитывая знаки приращений и поправок. Полученные значения записываются в графы 10 и 11. Суммируем исправленные значения приращений ∆x и ∆y. Контроль вычислений: линейные невязки f∆x и f∆y после увязки приращений координат должны равняться нулю. 5). Вычисление координат точек полигона Координаты точек полигона вычисляются по формулам: Хпосл. = Хпред.+ ∆xиспр.; Упосл. = Упред.+ ∆уиспр. Контролем служит вычисление координат первой точки, которые должны быть равны заданным Х I и У I. Пример расчета координаты Х: Для рассматриваемого примера формулы расчета координаты Х имеют вид: Х II = Х I + ∆x I- II = 200,00 + (- 42,49) = 157,51 Х III = Х II + ∆x II- III = 157,51 + (-110,92) = 46,59 Х IV = Х III + ∆x III- IV = 46,59 + (- 49,15) = - 2,56 Х V = Х4 + ∆x IV - V = (- 2,56) + 87,24 = 84,68 Контрольные вычисления координат первой точки и исходные координаты первой точки совпадают: Х I = Х V + ∆Х V- I = 84,68 + 115,32 = 200,00 Координаты точек записываются в графы 12 и 13 таблицы 3. В тетради для практических работ должны быть все промежуточные расчеты в соответствии с этапами вычислений и все заполненные таблицы. ВЫЧИСЛЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ Таблица 3
Σβ теор = 180° (n-2) = 180° ∙ (5-2) = 540° , где n– число углов fs = 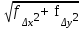 = 0,49 = 0,49 f β = Σβизм - Σβ теор = 1,1' fотн = 1/(Р: fs) = 1/(522,78: 0,48) ≈1 / 1067 f β доп = 2 t 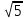 = 1'∙ = 1'∙ 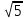 = 2,23' fдоп =1/1000 = 2,23' fдоп =1/1000ИСХОДНЫЕ ДАННЫЕ К ВЫЧИСЛЕНИЮ КООРДИНАТ Таблица 4
Таблица 5 Ведомость вычисления координат точек теодолитного хода
f факт=изм - теор = fx= Xпр - Xтеор = fy = Yпр - Yтеор = теор= 180(n-2) = 540 fабс = 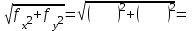 fдоп 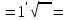 fотн = fотн = 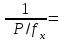 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||