Методические указания к практическим занятиям по металлургической теплотехнике. Метод_указ_Прак_Мет_теплотех. Методические указания к практическим занятиям по дисциплине Металлургическая теплотехника
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
Часть сообщенной теплоты 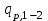 равная равная 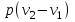 , переходит в работу расширения, а другая часть идет на увеличение внутренней энергии тела. , переходит в работу расширения, а другая часть идет на увеличение внутренней энергии тела.Изменение энтропии 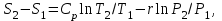 при 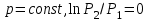 поэтому поэтому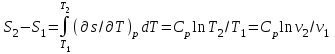 Изотермный процесс Процесс, протекающий при постоянной температуре, называют изотермным ( 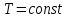 или или 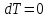 ). Кривая процесса называется изотермой . Для изотермного процесса идеального газа ). Кривая процесса называется изотермой . Для изотермного процесса идеального газа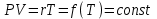 или или 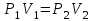 или или 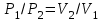 При постоянной температуре объем газа изменяется обратно пропорционально его давлению (закон Бойля-Мариотта). Количество подведенной к рабочему телу теплоты численно равно работе изменения объема. Удельная работа изменения объема равна 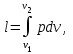 но из уравнения изотермы имеем 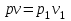 или или 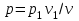 , поэтому , поэтому 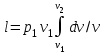 . .Интегрируя последнее уравнение, получаем 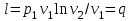 Теплоемкость в изотермическом процессе 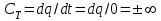 Теплота, участвующая в изотермном процессе, равна произведению изменения энтропии 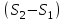 на абсолютную температуру T: на абсолютную температуру T: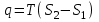 Адиабатный процесс Процесс, протекающий без подвода и отвода теплоты, т. е. при отсутствии теплообмена рабочего тела с окружающей средой, называют адиабатным, а кривая этого процесса называется адиабатой. Для получения адиабатного процесса необходимым и обязательным, условием является dq = 0 и q = 0. Обратимый адиабатный процесс можно, осуществить в цилиндре с абсолютно нетеплопроводными стенками при бесконечно медленном перемещении поршня. Уравнение адиабаты: откуда уравнение адиабаты 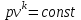 При адиабатном процессе произведение давления на объем газа в степени k есть величина постоянная. Величину k называют показателем адиабаты. Дифференциальное уравнение изоэнтропного процесса: 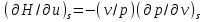 . .В этом уравнении 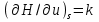 . .Теплоемкость в адиабатном процессе из выражения 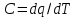 при при 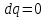 также равна нулю. также равна нулю.При обратимом адиабатном процессе идеального газа располагаемая внешняя работа будет в 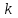 раз больше удельной работы изменения объема и обратна ей по знаку: раз больше удельной работы изменения объема и обратна ей по знаку: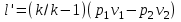 и и 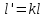 Политропные процессы Условились всякий процесс идеального газа, в котором удельная теплоемкость является постоянной величиной, называть политропным процессом, а линию процесса - политропой. Из определения политропного процесса следует, что основные термодинамические процессы - изохорный, изобарный, изотермический и адиабатный, - если они протекают при постоянной удельной теплоемкости, являются частными случаями политропного процесса. Теплоемкость политропного процесса Сп может принимать самые разнообразные положительные и отрицательные значения от + ∞ до — ∞. Количество теплоты, участвующее в политропном процессе, может быть выражено произведением теплоемкости процесса Сп на разность температур 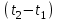 в конечном и начальном состояниях; в конечном и начальном состояниях;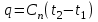 и и 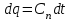 Уравнение политропного процесса 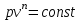 Показатель политропы n принимает для каждого процесса определенное числовое значение. Для основных процессов: изохорных n = ±∞, изобарных n=0, изотермных n = 1 и адиабатных n = k. Поскольку уравнение политропы отличается от уравнения адиабаты только величиной показателя n, то, очевидно, все соотношения между основными параметрами могут быть представлены аналогичными формулами: 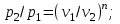 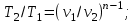 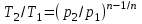 Теплоемкость политропного процесса определяем из формулы: 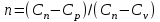 , откуда , откуда 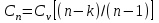 Если в уравнение подставить значения 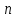 для частных случаев, то получаем теплоемкости рассмотренных процессов: для частных случаев, то получаем теплоемкости рассмотренных процессов:изохорного процесса 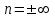 , , 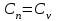 ; ;изобарного процесса 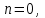 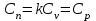 ; ;изотермного процесса 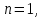 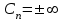 ; ;адиабатного процесса 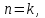 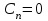 Уравнение работы изменения объема, при политропном процессе 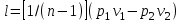 или 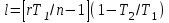 Изменение внутренней энергии газа и теплота в политропном процессе определяется по формулам: 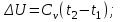 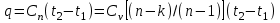 Располагаемая внешняя работа в политропном процессе равна 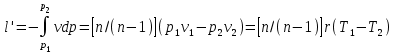 Изменение энтальпии в политропном процессе 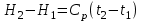 5.2 Примеры решения задач Задача № 1. В резервуаре емкостью 1 м3 находится воздух при давлении 0,5 МПа и температуре 20ºC. Как изменится температура и давление воздуха, если к нему подвести 175 кДж теплоты? Решение: Масса воздуха 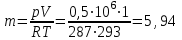 кг. кг.Если не учитывать зависимость теплоемкости от температуры, то 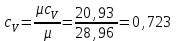 кДж/(кг·К). кДж/(кг·К).Повышение температуры при подводе теплоты в изохорном процессе 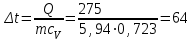 ºC. ºC.Следовательно, t2 = t1 + Δt = 20 + 64 = 84ºC = 357 К. Давление воздуха в конце изохорного нагревания 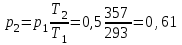 МПа. МПа.Задача № 2. В цилиндре двигателя внутреннего сгорания в конце сжатия абсолютное давление 1,6 МПа и температура 370ºC. Сгорание горючей смеси происходит при постоянном объеме с выделением 400 кДж теплоты на 1 кг смеси. Определить р, V, T в цилиндре в конце сгорания без учета зависимости теплоемкости от температуры. Считать, что продукты сгорания обладают свойствами воздуха. Решение: Удельный объем продуктов сгорания 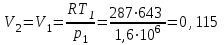 м3/кг. м3/кг.Температура после сгорания горючей смеси 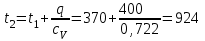 ºC. ºC.Конечное давление в цилиндре 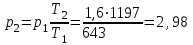 МПа. МПа. Какую мощность должен иметь электрический калорифер, чтобы нагревать при постоянном давлении рб = 750 мм рт. ст. поток воздуха от t1 = -20ºC до t2 = 20ºC, если производительность вентилятора на холодном воздухе V = 0,5 м3/с? Зависимость теплоемкости от температуры не учитывать. Решение: Массовая производительность вентилятора 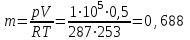 кг/с. кг/с.Мощность калорифера 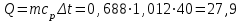 кВт. кВт.Задача № 3. Воздух, нагнетаемый первой ступенью двухступенчатого компрессора производительностью 0,1 м3/с, перед поступлением во вторую ступень сжатия охлаждается от t1 = 160 ºC до t2 = 40 ºC при постоянном давлении. Определить количество отводимой теплоты и работу уменьшения объема в результате охлаждения. Параметры окружающей среды: рб = 750 мм рт. ст.; t = 20 ºC. Решение: Массовая производительность компрессора 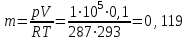 кг/с. кг/с.Отводимая теплота Q = mсрΔТ = 0,119·1,012·120 = 14,4 кДж/с. Работа уменьшения объема L = mRΔТ = 0,119·287·10-3·120 = 4,1 кДж/с. Задача № 4. При температуре t1 = 20 ºC 1 кг углекислоты сжимается изотермически до десятикратного уменьшения объема. Определить конечное давление, работу сжатия и отводимую теплоту, если начальное давление 0,1 МПа. Решение: Конечное давление для изотермического процесса определяется в соответствии с таблицей 1.4 по соотношению р2V2 = р1V1; 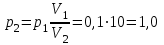 МПа. МПа.Так как в изотермическом процессе нет изменения внутренней энергии, то работа газа равна теплоте 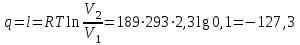 кДж/кг. кДж/кг.Задача № 5. Адиабатно расширяется 1 кг воздуха с температурой t1 = 20 ºC и давлением р1 = 0,8 МПа до давления р2 = 0,2 МПа. Определить параметры состояния в конце процесса расширения, работу процесса и изменение внутренней энергии газа. Решение: Температура в конце адиабатного расширения 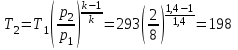 К = -75ºC. К = -75ºC.Удельный объем воздуха в конце расширения 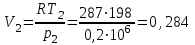 м3/кг. м3/кг.Работа адиабатного процесса 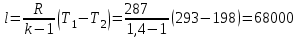 Дж. Дж.Изменение внутренней энергии 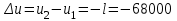 Дж. Дж.5.3 Задания для самостоятельного решения Задание №1. Баллон емкостью 60 л заполнен кислородом. Абсолютное давление кислорода р1 = 10 МПа при температуре t1 = 15ºC. Определить давление в баллоне и количество подведенной к кислороду теплоты, если температура в баллоне повысится до t2 = 40ºC. Ответ: Q = 131 кДж и р2 = 10,87 МПа. Задание №2. Колба электрической лампочки накаливания заполнена инертным газом. При работе лампочки средняя температура газа в колбе 150 ºC и давление 760 мм рт. ст. Определить разрежение в лампочке при температуре 20ºC и барометрическом давлении 745 мм рт. ст. Ответ: 218,6 мм рт. ст. Задание №3. Двигатель внутреннего сгорания работает с подводом теплоты при V = const. Параметры горючей смеси перед сгоранием р1 = 1,2 МПа; Т1 = 673 К. Определить расход теплоты на 1 кг горючей смеси и давление в конце сгорания, если Т2 = 2250 К. Продукты сгорания считать обладающими свойствами воздуха. Учесть зависимость теплоемкости продуктов сгорания от температуры. Ответ: q = 1547 кДж/кг; р2 = 4,012 МПа. Задание №4. В воздухоподогревателе котельной установки воздух нагревается от 20ºC до 250ºC при постоянном абсолютном давлении 0,1 МПа. Определить удельную работу расширения воздуха и расход теплоты на нагревание 1 кг воздуха, учитывая зависимость теплоемкости от температуры. Ответ: q = 234,6 кДж/кг; l = 66,0 кДж/кг. Задание №5. Воздух, подаваемый для вентиляции помещения, проходит электрокалорифер и нагревается от t1 = -20ºC до t2 = 15ºC при постоянном давлении 750 мм рт. ст. Определить производительность вентилятора, если мощность нагревателя калорифера 10 кВт. Теплоемкость воздуха принять постоянной. Ответ: 0,282 кг/с. Задание №6. Изотермическим сжатием 1 кг воздуха давление повышается от 0,1 МПа до 0,5 МПа. Определить уменьшение объема при 10ºC и при 100ºC. Ответ: ΔVt=10º = 0,649 м3; ΔVt=100º = 0,856 м3. Задание №7. Адиабатно сжимается 1 м3 воздуха до трехкратного уменьшения объема. Определить работу сжатия, а также давление и температуру в конце процесса сжатия, если р1 = 0,1 МПа и t1 = 10ºC. Ответ: Т2 = 440 К = 167ºC; р2 = 0,465 МПа; L = 139 кДж/м3. Контрольные вопросы: 1. Дать определения основным термодинамическим процессам. 2.Объяснить увеличение температуры при расширении газа в изобарном процессе. 3. Приведите уравнение политропного процесса. 4. Что такое показатель адиабаты. 5. Изобарный процесс. 6. Изохорный процесс. 7. Адиабатный процесс. Практическое занятие № 6 Передача тепла теплопроводностью 6.1 Краткие теоретические сведения Теплопроводность – это процесс распространения теплоты между соприкасающимися телами или частями одного тела с различной температурой. Для осуществления теплопроводности необходимы два условия: контакт и разница температур. Перенос теплоты теплопроводностью зависит от распределения температуры по объему тела. В общем виде температура зависит: t = f(x, y, z, ) , где x, y, z – координаты точки; - время Совокупность значений температуры во всех точках тела в данный момент времени называется температурным полем. Поверхность, во всех точках которой температура одинакова, называется изотермической. Быстрее всего температура изменяется при движении в направлении, перпендикулярном изотермической поверхности. Градиент температуры – это векторная величина, направленная по нормали к изотермической поверхности в сторону увеличения температуры и численно равная производной от температуры по этому направлению: Количество теплоты (Q), проходящее в единицу времени через изотермическую поверхность (F), называют тепловым потоком, обозначают Q*, единицы измерения – ватт. Тепловой поток, приходящийся на 1м2 поверхности, называют удельным тепловым потоком (плотностью теплового потока или тепловой нагрузкой поверхности нагрева), обозначают q, Вт/м2: Основной закон теплопроводности формулируется следующим образом: плотность теплового потока пропорциональна градиенту температуры (закон Фурье): q = - grad t , где - коэффициент пропорциональности, Вт/(м·К). Коэффициент пропорциональности называют коэффициентом теплопроводности. Он характеризует способность материала проводить тепло. Значения коэффициентов приводятся в справочниках теплофизических свойств веществ. Величина коэффициента теплопроводности зависит от температуры, для большинства материалов эта зависимость линейная: t = 0 (1 + b t) , где 0, t – значение коэффициента теплопроводности соответственно при 0 оС и при данной температуре t, Вт/(м·К); b – константа, определяемая экспериментально. Зависимость изменения температуры тела от свойств тела и координат точки описывает дифференциальное уравнение Фурье: 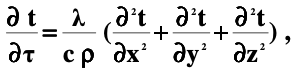 где - коэффициент теплопроводности, Вт/(м·К); - плотность материала, кг/м3; с- теплоемкость материала, Дж/(кг·К). Процесс теплоотдачи между поверхностью тела и окружающей средой описывается уравнением Ньютона-Рихмана: |
