Методические указания к практическим занятиям по металлургической теплотехнике. Метод_указ_Прак_Мет_теплотех. Методические указания к практическим занятиям по дисциплине Металлургическая теплотехника
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
7.2 Примеры решения задач Задача №1.Гладкая плита шириной b = 1 м и длиной L = 1,2 м обдувается воздухом со скоростью ω0 = 8 м/с. Определить средний коэффициент теплоотдачи 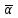 и полный тепловой поток Q, если температура стенки tc = 60 oC и температура воздуха tж = 20 oC. и полный тепловой поток Q, если температура стенки tc = 60 oC и температура воздуха tж = 20 oC.Решение: При tж = 20 oC имеем: λж = 0,0259 Вт/(м∙оС) и νж = 15,06∙10–6 м2/с. Критерий Рейнольдса определим по формуле: 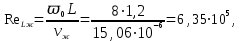 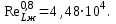 Подставляя эти значения для критерия Нуссельта при турбулентном режиме, получаем: 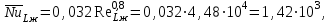 откуда откуда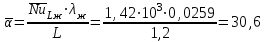 Вт/(м2 ∙ 0С). Вт/(м2 ∙ 0С).Тогда согласно закону Ньютона-Рихмана тепловой поток будет равен: 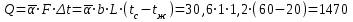 Вт = 1,47 кВт. Вт = 1,47 кВт.Задача №2.По трубопроводу диаметром d = 500 мм движется воздух со скоростью ω = 16 м/с. Температура воздуха 300 oC. Определить характеризующие процесс критерии Re, Pr, Pe. Решение: Re = ωd/ν Из справочных таблиц при 300 oC ν = 48,2*10-6 м2/с и критерий Pr = 0,72 для воздуха. Re = 16*0,5/48,2*10-6 = 160000. Pe = Re*Pr = 160000*0,72 = 115000. Движение турбулентное. Задача №3.Определить коэффициент теплоотдачи от воды к внутренней стенке трубы диаметром 17 мм, если температура стенки tс = 30 оС, а температура воды в трубе tж = 60 оС. Скорость воды в трубе ω = 0,5 м/с. Решение: При теплообмене в трубах определяющим критерием, характеризующим режим течения, является критерий Рейнольдса Re = ωd/ν = 0,5*0,017/0,478*10-6 = 17800. Так как режим движения турбулентный, то расчет теплообмена производится по формуле Nu = 0,021 Reж 0,8Prж 0,43(Prж /Prс)0,25 При температуре жидкости tж = 60 0С критерий Прандтля Prж = 2,98. При температуре стенки tс = 30 0С - Prс=5,42 (из справочника): Nu = 0,021 *17800 0,8 *2,980,43(2,98 /5,42)0,25 = 72,6 Так как Nu = αd/λж, то при λж = 65,9*10-2 (из справочника) α = 72,6*0,659/0,017 = 2810 Вт/ м2 ∙ К Задача №4.Температура поверхности вертикальной стенки высотой 3 м равна 10 оС.Температура воздуха в помещении 20 оС.Определить коэффициент теплоотдачи от воздуха к стенке. Решение: Теплообмен осуществляется при свободной конвекции. Определим значение критериев Grж и Prж. Grж = gβΔtl3/ν2ж = 9,81*10*33/293(15,06*10-6) 2 = 3,98*1010 Prж = 0,701; Grж * Prж =2,79*1010 Определяем коэффициент теплоотдачи Nuж = 0,15 (Grж * Prж)0,33(Prж /Prс)0,25 = 0,15(2,79*1010)0,33*1 = 423 α = Nuж λж/h = 423*0,02593/3 = 3,66 Вт/ м2 ∙ К. Задача №5.По трубе d 60 мм протекает воздух со скоростью w 5 м/с. Определить значение среднего коэффициента теплоотдачи, если средняя температура воздуха Tf 100 оC. Решение: За определяющую температуру принимаем T0 Tf 100 оC. При определяющей температуре воздух имеет свойства (по справочнику): 0,0321 Вт/(моС); 23,1310-6 м2 /с. За определяющей размер принимаем диаметр трубы R0 d 0,06 м. Критерий Рейнольдса так как Re 104, то режим течения турбулентный. Критерий Нуссельта Nu 0,018Rе0,8 0,0181955 35,2. 7.3 Задания для самостоятельного решения Задание № 1. Рассчитать потерю теплоты конвекцией в единицу времени с 1м2 поверхности горизонтального теплообменника, корпус которого имеет цилиндрическую форму и охлаждается свободным потоком воздуха. Наружный диаметр корпуса теплообменника d 400 мм, температура поверхности Tw 160 оC , температура воздуха в помещении Tf 20 оC. Ответ: 7,3 Вт/(м К); q 1025 Вт/м2. Задание № 2. По условию задания 1 в целях уменьшения тепловых потерь корпус теплообменника покрыт слоем тепловой изоляции. Найти тепловые потери q, Вт/м2 с поверхности теплообменника, если после наложения слоя тепловой изоляции толщиной 50 мм температура на внешней поверхности изоляции Tw стала равна 40 оС, а температура в помещении Tf осталась прежней + 20 оC. Ответ: q 86 Вт/м . Задание № 3. Определить коэффициент теплоотдачи от вертикальной плиты высотой H 1,5 м к окружающему воздуху, если известно, что температура поверхности плиты Tw 80 оC , температура окружающего воздуха вдали от поверхности Tf 20 оC . Ответ: 6 Вт/(м2 К). Задание № 4. Как изменится коэффициент теплоотдачи от вертикальной плиты к окружающему воздуху в условиях задачи 3, если высоту плиты увеличить в 4 раза, а все другие условия оставить без изменения? Ответ: 1 /2 1. Задание № 5. Водяной калориметр, имеющий форму трубки, с наружным диаметром d 16 мм помещён в поперечный поток воздуха. Воздух движется со скоростью w 3 м/с под углом 90о к оси калориметра и имеет среднюю температуру Tf 20 оC. При стационарном тепловом режиме на внешней поверхности калориметра устанавливается постоянная средняя температура T w 80 оC . Вычислить коэффициент теплоотдачи от трубки к воздуху и тепловой поток на единицу длины калориметра. Ответ: 46,9 Вт/(м2К); q 141,37 Вт/м. Контрольные вопросы: По величине какого критерия можно судить о характере конвективного режима? Как связаны между собой величина теплового потока при конвективном теплообмене и коэффициент теплопередачи? Для чего необходимо определять величину критерия Нуссельта? В каких случаях используют критерий Рейнольдса? Что характеризует критерий Прандтля? Что подразумевают под критериями подобия? Практическое занятие № 8 Теплообмен излучением 8.1 Краткие теоретические сведения Тепловое излучение (радиационный теплообмен) – способ переноса теплоты в пространстве, осуществляемый в результате распространения электромагнитных волн, энергия которых при взаимодействии с веществом переходит в тепло. Радиационный теплообмен связан с двойным преобразованием энергии: первоначально внутренняя энергия тела превращается в энергию электромагнитного излучения, а затем, после переноса энергии в пространстве электромагнитными волнами, происходит второй переход лучистой энергии во внутреннюю энергию другого тела. Тепловое излучение вещества зависит от температуры тела (степени нагретости вещества). Энергия теплового излучения, падающего на тело, может поглощаться, отражаться телом или проходить через него. Тело, поглощающее всю падающую на него лучистую энергию, называют абсолютно черным телом (АЧТ). Отметим, что при данной температуре АЧТ и по- глощает, и излучает максимально возможное количество энергии. Плотность потока собственного излучения тела называют его лучеиспускательной способностью. Этот параметр излучения в пределах элементарного участка длин волн d называют спектральной плотностью потока собственного излучения или спектральной лучеиспускательной способностью тела. Лучеиспускательная способность АЧТ в зависимости от температуры подчиняется закону Стефана-Больцмана: 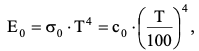 где 0 = 5,6710-8 Вт/(м2К4) – постоянная Стефана-Больцмана; c0 = 5,67 Вт/(м2К4) – коэффициент излучения абсолютно черного тела; Т – температура поверхности абсолютно черного тела, К. Абсолютно черных тел в природе не существует. Тело, у которого спектр излучения подобен спектру излучения абсолютно черного тела и спектральная плотность потока излучения (Е) составляет одну и ту же долю от спектральной плотности потока излучения абсолютно черного тела (Е0,λ), называют серым телом. 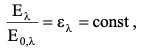 где – спектральная степень черноты. После интегрирования последнего выражения по всему спектру излучения ( 0 ) получим где Е – лучеиспускательная способность серого тела; Е0 – лучеиспускательная способность АЧТ; – интегральная степень черноты серого тела или степень черноты. Степень черноты – экспериментально определяемая величина в зависимости от физических свойств тела, его температуры и шероховатости поверхности приведена в справочнике. Выражение для расчета плотности потока собственного излучения (лучеиспускательной способности) серого тела: 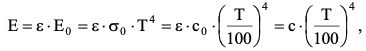 где c c0 – коэффициент излучения серого тела, Вт/(м2К4); Т – температура тела, К. Теоретические положения по расчету радиационного теплообмена в замкнутой системе, состоящей из серых поверхностей, разделенных лучепрозрачной средой, подробно изложены в научной литературе. Поток результирующего излучения в замкнутой системе, состоящей из двух серых поверхностей, разделенных диатермичной средой, рассчитывают по формуле или 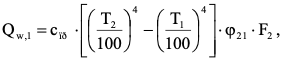 где Т – абсолютная температура поверхности теплообмена, К; F – площадь поверхности теплообмена; 12 и 21 – угловые коэффициенты излучения соответственно с первого тела на второе и со второго тела на первое ; пр – приведенная степень черноты в системе двух тел; cпр 0 пр – приведенный коэффициент излучения в системе двух тел. Приведенная степень черноты и приведенный коэффициент излучения в замкнутой системе радиационного теплообмена, состоящей из двух серых тел, рассчитывают по формулам: 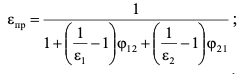 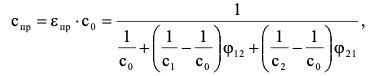 Угловые коэффициенты излучения в системе, состоящей из двух поверхностей, удобно рассчитывать, используя свойства угловых коэффициентов: а) свойство замкнутости б) свойство взаимности в) свойство невогнутости (для плоских и выпуклых поверхностей) ii 0. Для замкнутой системы радиационного теплообмена, состоящей из двух тел, справедливо равенство Qw,2 Qw,1. 8.2 Примеры решения задач Задача №1. Определить приведенную степень черноты системы, состоящей из двух труб, если одна труба с наружным диаметром d1 = 80 мм находится внутри другой с внутренним диаметром d2 = 200 мм. Степень черноты труб одинакова и равна 0,65. Решение: Наружную поверхность внутренней трубы обозначим через F1, а внутреннюю поверхность наружной трубы F2. Приведенную степень черноты определяем по формуле 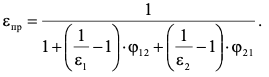 Для внутренней трубы угловой коэффициент 12 1. Для наружной трубы угловой коэффициент излучения 21 рассчитываем по формуле: 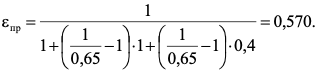 Задача №2. Определить плотность результирующего теплового потока при теплообмене излучением двух плоских поверхностей, если температура одной поверхности 800 оС, ее степень черноты 0,8 и температура другой поверхности 600 оС, а её степень черноты 0,4. Решение: Плотность результирующего теплового потока излучением определяется по формуле Приведенная степень черноты 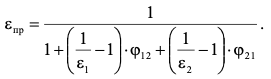 Для плоских поверхностей 21 12 1. 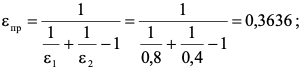 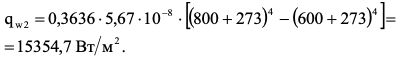 Задача №3. Сколько теплоты теряет в час 1 м2 вертикальной поверхности обмуровки котла, если температура стенки 100 оС, а температура воздуха 30 оС. При этом коэффициент конвективной теплоотдачи равен 4,5 Вт/(м2 ·К). Степень черноты обмуровки котла 0,78. Решение: Плотность теплового потока излучением Используем свойство угловых коэффициентов излучения: 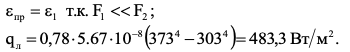 Плотность теплового потока конвекцией Суммарная плотность теплового потока конвекцией и излучением 1 м2 поверхности обмуровки за час теряет теплоты: Задача №4. Определить собственную излучательную способность стен- ки летательного аппарата с коэффициентом излучения 4,53 Вт/(м2 *К4), если температура поверхности стенки 1027 оС. Определить также степень черноты стенки и длину волны, отвечающей максимуму интенсивности излучения. Решение: Излучательную способность стенки летательного аппарата определяем по формуле: Степень черноты определяем из равенства ε CS = C , Откуда Длину волны, отвечающую максимуму интенсивности излучения, определяем из закона Вина: |
