Методические указания к практическим занятиям по металлургической теплотехнике. Метод_указ_Прак_Мет_теплотех. Методические указания к практическим занятиям по дисциплине Металлургическая теплотехника
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН Казахский национальный исследовательский технический университет имени К.И. Сатпаева Горно-металлургический институт им. О.А. Байконурова Кафедра металлургических процессов, теплотехники и технологии специальных материалов Г.А. Усольцева, Т.А. Чепуштанова, А.Ж. Алтмышбаева Металлургическая теплотехника Методические указания к практическим занятиям по дисциплине «Металлургическая теплотехника» (для студентов специальности «6В07203 – Металлургия и обогащение полезных ископаемых») Алматы 2021 ВВЕДЕНИЕ Методические указания являются руководством по практическим занятиям для студентов, изучающих курс «Металлургическая теплотехника» по специальности «6В07203 – Металлургия и обогащение полезных ископаемых», а также могут быть полезны студентам других специальностей, изучающим теплотехнические дисциплины. Методические указания охватывают основные разделы теоретического курса. В методических указаниях приведено краткое описание теоретических положений и основные расчетные формулы, даны примеры решения типовых задач по представленным тематикам. Перечень практических занятий определяется преподавателем в соответствии с силлабусом дисциплины и содержит разделы технической термодинамики и металлургической теплотехники. Теплотехника – наука, изучающая способы получения теплоты, преобразования, передачи и использования ее, а также тепловую работу печей, теплообменных аппаратов, нагревательных устройств. Теплотехника – область науки и техники, охватывающая процессы и оборудование, служащие для использования тепловых явлений в промышленных, сельско-хозяйственных, бытовых или иных целях. Основа теплотехники – теория теплообмена и техническая термодинамика. Теплообмен – самопроизвольный необратимый процесс переноса теплоты, обусловленный градиентом температуры, процесс переноса теплоты от более нагретых тел к менее нагретым. Учение о теплообмене – это учение о процессах распространения тепла. Отличительной их особенностью является универсальность, так как они имеют весьма большое значение почти во всех отраслях техники. Процесс теплообмена – сложный процесс, состоящий из трех элементарных видов теплообмена – теплопроводности, конвекции и теплового излучения (лучеиспускания). Практическое занятие № 1 Рабочее тело и его основные параметры 1.1 Краткие теоретические сведения Физическое состояние рабочего тела определяется тремя параметрами состояния: температурой, давлением и удельным объемом. Температура характеризует тепловое состояние тела и измеряется в градусах. Численное значение температуры зависит от принятой температурой шкалы. Используются температурные шкалы: абсолютная или термодинамическая – Т, К; Цельсия или стоградусная (называемая также международной практической шкалой) - t, оС; шкала Фаренгейта – t, °F и др. Абсолютная температура тела Т, К= t, °С + 273,15. По шкале Фаренгейта, принимаемой в Англии и США, температура плавления льда 32 °F и температура кипения воды 212 °F, следовательно, t, °C = 5/9 (t, °F - 32). Давление – это сила, действующая по нормали на единицу поверхности. Единицей давления в системе СИ является паскаль, представляющий давление силы в 1 ньютон на площадь в 1м², т.е. 1Н/м². Давление измеряется манометрами, если оно больше атмосферного, или вакуумметрами, если меньше. Абсолютное давление рабс, если оно больше атмосферного (барометрического) рб, определяется как сумма рабс = рб + рм, где рм – показание манометра, измеряющего избыточное давление. Если рабс рб, то рабс = рб + рв, где рв – показание вакуумметра, измеряющего разрежение. Удельный объем, или объем единицы массы 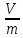 , ,где V и m – соответственно объем тела и его масса. Нормальные физические условия соответствуют: tн = 0 °C и pн = 1 атм =101 325 Па = 101 325 Н/м² = 760 мм рт. ст. Связь между единицами измерения давления представлена в таблице 1. Таблица 1 - Связь между единицами измерения давления*
*https://ru.wikipedia.org/wiki/Паскаль_(единица_измерения) Перевод внесистемной единицы «кгс/см2» в паскали: 1,0197*10-6 кгс/см2 = 1 Па. 1.2 Примеры решения задач Задача №1. Определить абсолютное давление газа в резервуаре, если ртутный манометр показывает избыточное давление 300 Па, а барометр 750 Па. Решение: Абсолютное давление в резервуаре pабс больше барометрического, поэтому равно сумме избыточного манометрического рм и барометрического рб давлений рабс = рм + рб = 1050 мм рт. ст. = 0,143 МПа. Задача №2. При барометрическом давлении 760 мм рт. ст. манометр, установленный на баллоне с газом, показывает 0,2 кгс/см2. Как изменится показание манометра, если барометрическое давление упадет до 730 мм рт. ст.? Решение: При изменении барометрического (атмосферного) давления абсолютное давление в резервуаре не изменится, но избыточное давление, представляющее разность между абсолютным и барометрическим, увеличится на р = 760 - 730 = 30 мм рт. ст. = 4 кПа. Следовательно, рм2 = рм1 + р = 20 + 4 = 24 кПа. Задача №3. Чему равно абсолютное давление в резервуаре, если при температуре 30 С ртутный манометр показывает 1200 мм, а ртутный барометр – 750 мм? Температурное расширение ртути учитывать по формуле h0 = h (1-0,000172t). Решение: Без учета поправки на температурное расширение ртути рабс = рм + рб = 1200 + 750 = 1950 мм рт. ст. = 0,265 МПа. С учетом поправки рабс = 0,265 (1 - 0,000172·30) = 0,261 МПа. Задача № 4. В сосуде объемом 0,9 м3 находится 1,5 кг оксида углерода (II) - СО. Определить удельный объем и плотность оксида углерода (II). Решение: Удельный объем оксида углерода (II): 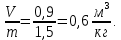 Плотность оксида углерода (II): 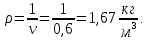 1.3 Задания для самостоятельного решения Задание №1. Определить показание ртутного вакуумметра, присоединенного к конденсатору паровой турбины при барометрическом давлении 750 мм рт. ст., если абсолютное давление в конденсаторе 3,6 кПа и температура в месте установки вакуумметра 25°С. Ответ: рв = 726 мм рт. ст. Задание №2. В тягомере, присоединенном к газоходу котла, длина столба воды в трубке, наклоненной под углом 30 к горизонту, 136 мм. Определить абсолютное давление рабс в газоходе котла при барометрическом давлении 740 мм рт. ст. Ответ:рабс = 98 кПа. Задание №3. Давление в паровом котле Р = 0,4 бар при барометрическом давлении 725 мм рт. ст. Чему будет равно избыточное давление в котле, если показание барометра повысится до 785 мм рт. ст., а состояние пара в котле останется прежним? Барометрическое давление приведено к 0 °С. Ответ: Ризб = 136642 – 785 * 133,3 = 32000 Па. Задание №4. Найти абсолютное давление пара в котле, если манометр показывает рм = 0,13 МПа. Атмосферное давление по показаниям ртутного барометра составляет рв = 730 мм рт. ст. при t = 25 0С. Ответ: рабс =0,227 МПа. Контрольные вопросы: Какими параметрами определяется физическое состояние рабочего тела? Что подразумевают под термином «температура»? Как определяют абсолютное давление? Дайте определение удельному объему тела. В чем разница между манометрическим, барометрическим и абсолютным давлением? Назовите параметры нормальных физических условий. Температурные шкалы и связь между ними Практическое занятие № 2 Законы идеальных газов 2.1 Краткие теоретические сведения Идеальный газ - математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией; суммарный объём молекул газа пренебрежимо мал; между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц. В рамках термодинамики идеальным называется газ, подчиняющийся термическому уравнению состояния Клапейрона-Менделеева. Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми-Дирака или Бозе-Эйнштейна). Закон Бо́йля-Марио́тта - один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Описывает поведение газа в изотермическом процессе. Закон гласит, что при постоянных температуре и массе газа произведение давления газа на его объём постоянно: PV = const или P1V1 = P2V2, где P - давление газа; V - объём газа, const - постоянная в оговоренных условиях величина. В общем случае ее значение определяется химической природой, массой и температурой газа. А связь начального и конечного состояний газа, участвовавшего в изотермическом процессе, можно выразить в виде: P1 / P2 = V2 / V1 Закон Гей-Люссака - закон пропорциональной зависимости объёма газа от абсолютной температуры при постоянном давлении, названный в честь французского физика и химика Жозефа Луи Гей-Люссака. Гей-Люссак опубликовал его в 1802 г. и первым продемонстрировал, что закон применим ко всем газам, а также к парам летучих жидкостей при температуре выше точки кипения. Математически он выразил своё открытие так: где V100 - объём данного количества газа при температуре 100 °C; V0 - объём того же газа при 0 °C; k - константа, одинаковая для всех газов при одинаковом давлении. Гей-Люссак дал для константы k значение 1/266,66, что достаточно близко к современному значению, равному 1/273,15. Изобарический закон, открытый Гей-Люссаком в 1802 году утверждает, что при постоянном давлении, объём постоянной массы газа пропорционален абсолютной температуре:  Зако́н Ша́рля или второй закон Гей-Люссака - один из основных газовых законов, описывающий соотношение давления и температуры для идеального газа. Экспериментальным путем зависимость давления газа от температуры при постоянном объёме установлена в 1787 году Шарлем и уточнена Гей-Люссаком в 1802 году. Формулировка закона Шарля следующая: давление газа фиксированной массы и фиксированного объёма прямо пропорционально абсолютной температуре газа. Проще говоря, если температура газа увеличивается, то и его давление тоже увеличивается, если при этом масса и объём газа остаются неизменными: где P - давление газа, T - температура газа (в градусах Кельвина), k - константа. Закон Авога́дро - одно из важных основных положений химии, гласящее, что «в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул», было сформулировано ещё в 1811 году Амедео Авогадро (1776-1856), профессором физики в Турине. Первое следствие из закона Авогадро: один моль любого газа при одинаковых условиях занимает одинаковый объём. В частности, при нормальных условиях, т. е. при 0 °C (273 К) и 101,3 кПа, объём 1 моля газа равен 22,4 л. Этот объём называют молярным объёмом газа Vm. Второе следствие из закона Авогадро: молярная масса первого газа равна произведению молярной массы второго газа на относительную плотность первого газа ко второму. При постоянных температуре и давлениях, справедливо:  Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева-Клапейрона) - формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: где p - давление, VM- молярный объём, R - универсальная газовая постоянная T - абсолютная температура, К. Так как где ν - количество вещества, где m - масса, M - молярная масса, уравнение состояния можно записать: рV = mRT/M или PV = nRT (n – число молей вещества) Эта форма записи носит имя уравнения (закона) Менделеева-Клапейрона. Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную r, значение которой необходимо было измерять для каждого газа: рV = rT. Менделеев же обнаружил, что r прямо пропорциональна ν, коэффициент пропорциональности R он назвал универсальной газовой постоянной. Уравнение состояния тела устанавливает зависимость между параметрами состояния. Для идеального газа уравнение состояния выражается законом Клайперона: а) для 1 кг газа p = RT, где R - газовая постоянная; б) для m кг газа pV mRT. Для моля идеального газа уравнение состояния предложено Менделеевым PV RT, где V - объем моля газа; - молекулярная масса. При нормальных физических условиях V = 22,4 м³/кмоль. Универсальная газовая постоянная R = 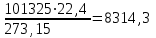 Дж/(кмоль К) Дж/(кмоль К)Газовая постоянная R =  . .Таблица 2.1 - Значения и R для некоторых газов
Объем газа V, находящегося при произвольных физических условиях (р и Т), может быть приведен к нормальным физическим условиям (рН и ТН) по формуле VH = 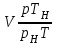 . .2.2 Примеры решения задач Задача № 1. Аэрозонд заполнен водородом, имеющим параметры окружающей среды р1 = 0,1 МПа, t1 = 30°С. Определить подъемную силу, приходящуюся на каждый кубический метр объема аэрозонда. Как изменится подъемная сила в зимних условиях при t = -30°С? Решение: Подъемная сила, приходящаяся на 1 м3 объема аэрозонда, зависит от разности плотностей в и н. Плотности определяются по уравнению состояния. Тогда подъемная сила = 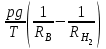 . .Для летних условий 1 = 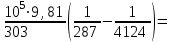 10,5 Н/м3. 10,5 Н/м3.Для зимних условий 2 = 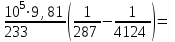 13,08 Н/м3. 13,08 Н/м3.Задача № 2. Два кислородных баллона одинакового объема соединены трубопроводом. Определить давление, которое установится в баллонах при температуре t = 25С, если до соединения параметры газа в первом баллоне были р1 = 8,0 МПа и t1 = 30°С, а во втором – р2 = 6,0 МПа и t2 = 20°С. Решение: Масса кислорода в баллонах m = m1 + m2 = 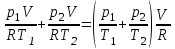 . .Давление в баллонах после их соединения 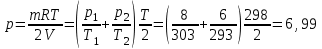 МПа. МПа.Задача № 3. Определить расход метана в газопроводе диаметром d = 800 мм, если скорость газа v = 15 м/с, абсолютное давление рабс = 5 МПа и температура 20°С. Решение: Площадь поперечного сечения газопровода Плотность метана Массовый расход метана m = Fv = 0,502·32,9·15 = 247,5 кг/с. Задача № 4. Во сколько раз объем определенной массы газа при -20 °С меньше, чем при +20°C, если давление в обоих случаях одинаковое? Решение: При постоянном давлении объем газа изменяется по уравнению: 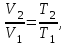 следовательно следовательно  Задача № 5. Какова будет плотность окиси углерода при 20 °С и 710 мм рт. ст., если при 0 °С и 760 мм рт. ст. она равна 1,251 кг/м3? Решение: Согласно уравнению 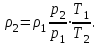 Следовательно, 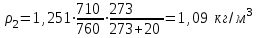 2.3 Задания для самостоятельного решения Задание №1. Сосуд емкостью 10 м3 заполнен 25 кг углекислого газа. Определить абсолютное давление в сосуде, если температура в нем 27 °С. Ответ: Р = 141700 Па Задание №2. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 15 °С. После расходования части кислорода давление понизилось до 7,6 МПа, а температура упала до 10 °С. Определить массу израсходованного кислорода. Ответ: расход кислорода составит m = 0,606 кг. Задание №3. Во сколько раз объем определенной массы газа при -20 °С меньше, чем при +20°C, если давление в обоих случаях одинаковое? Ответ: V1/V2 = 1,6. Задание №4. Какое количество воздуха должно быть подано компрессором в баллон емкостью 20 л, чтобы при температуре 18°С и барометрическом давлении 750 мм рт. ст. давление в нем повысилось с 1 МПа до 2 МПа? Ответ: m = 0,24 кг. Контрольные вопросы: 1. Универсальная газовая постоянная. 2. Уравнение состояния идеальных газов. 3. Закон Бойля-Мариотта. 4. Закон Гей-Люссака для идеальных газов. 5. Закон Шарля. 6. Закон Авогадро. Практическое занятие № 3 Первый и второй законы термодинамики 3.1 Краткие теоретические сведения Первый закон термодинамики является частным случаем общего закона сохранения и превращения энергии применительно к процессам взаимного превращения теплоты и работы. Закон утверждает, что сумма всех видов энергии изолированной системы при любых происходящих в системе процессов остается постоянной W = const; dW = 0. При осуществлении термодинамического процесса подводимая к телу теплота Q идет на изменение его внутренней энергии и совершение механической работы Q = ΔU + L. Для 1 кг рабочего тела q = Δu + l. Второй закон термодинамики устанавливает направление протекания самопроизвольных тепловых процессов в природе и определяет условия превращения теплоты в работу. Закон утверждает, что теплота в природе самопроизвольно переходит только от тел более нагретых к менее нагретым. В соответствии со вторым законом термодинамики для превращения теплоты в работу в любом тепловом двигателе необходимо иметь два тела с различными температурами. Более нагретое тело будет источником теплоты для получения работы, менее нагретое – теплоприемником. При этом КПД теплового двигателя всегда будет меньше единицы. Термический КПД теплового двигателя  , ,где Q1 и Q2 – соответственно теплота, подведенная в цикле и отведенная теплоприемнику. Для идеального цикла теплового двигателя, т.е. для прямого обратимого цикла Карно, 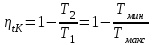 , ,где Т1 = Тмакс – температура горячего источника теплоты; Т2 = Тмин – температура холодного источника теплоты или теплоприемника. Термический КПД любого реального цикла теплового двигателя всегда меньше термического КПД цикла Карно для того же интервала температур. Важнейшим параметром состояния вещества является энтропия S. Изменение энтропии в обратимом термодинамическом процессе определяется уравнением, являющимся аналитическим выражением второго закона термодинамики 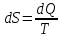 . .Для 1 кг вещества 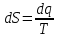 , ,где dq – бесконечно малое количество теплоты, подводимой или отводимой в элементарном процессе при температуре Т, кДж/кг. Энтропия является функцией состояния, поэтому ее изменение в термодинамическом процессе определяется только начальными и конечными значениями параметров состояния. Изменение энтропии в основных термодинамических процессах в изохорном 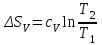 ; ;в изобарном  ; ;в изотермическом 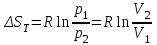 ; ;в адиабатном 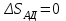 ; ;в политропном 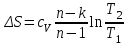 . .3.2 Примеры решения задач Первый закон термодинамики Задача № 1. В процессе расширения с подводом 120 кДж теплоты 1 кг воздуха совершает работу, равную 90 кДж. Определить изменение температуры воздуха в процессе, пренебрегая зависимостью теплоемкости от температуры. Решение: В соответствии с первым законом термодинамики теплота, подводимая к телу, идет на совершение работы и изменение внутренней энергии тела q = Δu + l. Так как Δu = сVΔt, где 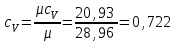 кДж/(кг·К), то кДж/(кг·К), то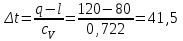 ºC. ºC.Задача № 2. Определить расход воздуха в системе охлаждения дизеля мощностью N = 38 кВт, если отводимая теплота составляет 75% полезной мощности двигателя, а температура охлаждающего воздуха повышается на 15ºC. Решение: Теплота, отводимая в системе охлаждения: Q = 0,75·38 = 28,5 кДж/с. Из уравнения теплового баланса воздуха, охлаждающего двигатель, находим:  кг/с. кг/с.Второй закон термодинамики Задача № 3. При постоянном давлении (равном 760 мм рт. ст.) к 1 кг азота, имеющему температуру 25ºC, подводится 100 кДж теплоты. Определить начальное значение энтропии и ее изменение в процессе. Решение: Изменение температуры в изобарном процессе 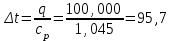 ºC. ºC.Изменение энтропии в изобарном процессе 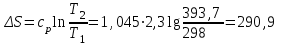 Дж/(кг·К). Дж/(кг·К).Начальное значение энтропии определяется по формуле изменения энтропии в процессе. За уровень отсчета принимаются нормальные физические условия, т.е. Sнфу = S0 = 0; ΔS0-1 = S1 - S0 = S1;  Дж/(кг·К). Дж/(кг·К).Задача № 4. При температуре 10ºC 3 кг воды смешиваются с 2 кг воды при температуре 80ºC. Определить возрастание энтропии из-за необратимости процесса смешения, при котором теплота переходит самопроизвольно от более нагретого тела к менее нагретому. Решение: Температура воды после смешения определяется из теплового баланса 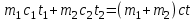 . .Теплоемкость воды в рассматриваемом интервале изменения температуры можно принять постоянной. Следовательно, 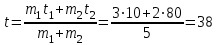 ºC. ºC.Тогда изменение энтропии отдельных масс воды 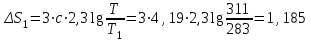 кДж/К; кДж/К;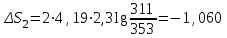 кДж/К. кДж/К.Общее изменение энтропии 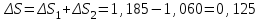 кДж/К. кДж/К.Задача № 5. В цикле Карно подвод теплоты происходит при максимальной температуре Т1 = 1200ºC. Полезная работа, получаемая в цикле, 265 кДж. Определить термический КПД. Подводимую и отводимую теплоту, а также минимальную температуру Т2, если рабочее тело – 1 кг воздуха, а относительное изменение объема в изотермических процессах равно 3. Решение: Для процесса изотермического расширения с подводом теплоты 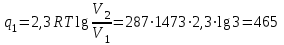 кДж/кг. кДж/кг.Термический КПД 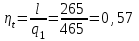 . .Отводимая теплота 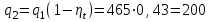 кДж/кг. кДж/кг.Низшая температура в цикле 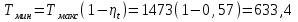 К. К.3.3 Задания для самостоятельного решения По первому закону термодинамики Задание № 1. Теплота сгорания дизельного топлива 42 000 кДж/кг. Определить работу, которую можно получить при использовании его в тепловом двигателе с КПД 45%. Ответ: L = 5,25 кВт·ч. Задание № 2. При расщеплении 1 кг урана в реакторе атомной электростанции количество выделяемой теплоты оценивается величиной 22,9·106 кВт·ч/кг. Определить, какое количество угля с теплотой сгорания 29300 кДж/кг потребуется для получения такого же количества теплоты. Ответ: 2813 т. Задание № 3. При испытании двигатель внутреннего сгорания мощностью 100 л. с. нагружается тормозом с водяным охлаждением. Определить расход охлаждающей воды, если температура ее при прохождении через тормоз повышается на 40ºC, а 15% теплоты от тормоза отводится воздухом в окружающую среду. Ответ: 0,373 кг/с. По второму закону термодинамики Задание № 4. Для цикла Карно, совершающегося в интервале температур 900ºС и 50ºC и давлений 1,0 МПа и 0,1 МПа, определить термический КПД, подводимую и отводимую теплоту на 1 кг рабочего тела, в качестве которого принят азот. Ответ: q1 = 510,4 кДж/кг; q2 = 140,6 кДж/кг; ηt = 0,725. Задание № 5. Цикл Карно совершается с 1 кг воздуха в пределах температур 927ºC и 27ºC. Подводимая в цикле теплота 30 кДж. Определить максимальное давление в цикле, термический КПД и полезную работу, если минимальное давление в цикле 0,1 МПа. Ответ: рмакс = 12,8 МПа; ηt = 0,75; l = 22,5 кДж/кг. Задание № 6. Термический КПД цикла теплового двигателя ηt = 0,4 и отводимая теплота Q2 = 120 кДж. Определить подводимую в цикле теплоту и полезную работу. Ответ: Q1 = 200 кДж; L = 80 кДж. Контрольные вопросы: Сформулируйте первое начало термодинамики. Перечислите известные Вам термодинамические процессы. Сформулируйте второе начало термодинамики. Дайте понятие энтропии. Цикл Карно. Практическое занятие № 4 Теплоемкость и ее роль в тепловых процессах 4.1 Краткие теоретические сведения Теплоемкостью тела называется количество теплоты, необходимое для повышения его температуры на 1 градус. Теплоемкость единицы количества вещества называется удельной теплоемкостью. Различают удельные теплоемкости массовую – с, кДж/(кг·К); объемную – С, кДж/(м3·К); мольную – μс, кДж/(моль·К): 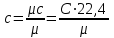 . .В теплотехнике принято удельную теплоемкость называть просто теплоемкостью. Теплоемкость зависит от природы рабочего тела, его температуры и характера процесса, в котором происходит подвод или отвод теплоты. Теплоемкость газов с повышением температуры увеличивается. Если 1 кг газа нагревается от t1 ºС до t2 ºС с подводом теплоты q, кДж, то средняя теплоемкость с| 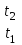 газа в рассматриваемом интервале температур t1 - t2 определяется по формуле газа в рассматриваемом интервале температур t1 - t2 определяется по формулес| 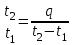 . .Теплоемкость тела, соответствующая определенной температуре, называется истинной теплоемкостью. Зависимость истинной теплоемкости газа от температуры имеет вид 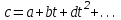 , ,где a, b, d – постоянные для каждого газа коэффициенты. Средняя теплоемкость в интервале температур t1 - t2: с| 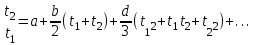 Для интервала температур 0 – t: с| 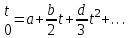 Если известны табличные значения средней теплоемкости с| 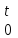 , то средняя теплоемкость в интервале t1 - t2: , то средняя теплоемкость в интервале t1 - t2: с|  . .Особое значение в термодинамике имеют теплоемкости газа при постоянном давлении, т.е. в изобарном процессе – сРи при постоянном объеме, т.е. в изохорном процессе – сV. Эти теплоемкости связываются формулой Майера 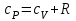 . .Отношение теплоемкостей 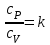 , ,где k – показатель адиабаты. Теплоемкость смеси идеальных газов а) массовая теплоемкость смеси 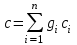 ; ;б) объемная теплоемкость смеси 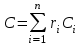 . .Теплоемкость рабочего тела в политропном процессе 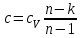 , ,где n – показатель политропы. Теплота нагревания газа 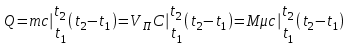 , ,где М – число молей газа. Если не учитывать зависимость теплоемкости газов от температуры, то можно пользоваться таблицей 4.1. Таблица 4.1- Мольные теплоемкости газов
Интерполяционные формулы для расчета истинных и средних мольных теплоемкостей газов приведены в таблице 4.2. Таблица 4.2 - Интерполяционные формулы для расчета истинных и средних мольных теплоемкостей газов в интервале температур 0 – 1000 ºС
4.2 Примеры решения задач Задача № 1. Сравните истинную при 1000ºС и среднюю в интервале 100 - 1000ºС массовую изобарную теплоемкость воздуха, принимая зависимость теплоемкости от температуры линейной (таблица 4.2). Решение: Молекулярная масса воздуха μВ = 28,96. Мольная истинная теплоемкость воздуха при постоянном давлении 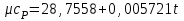 . .При t = 100 ºС 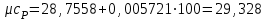 кДж/(кмоль·К); кДж/(кмоль·К);сР = 1,012 кДж/(кг·К). При линейной зависимости теплоемкости от температуры средняя мольная теплоемкость определяется по формуле 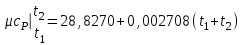 . .В интервале 100 – 1000 ºС 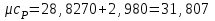 кДж/(кмоль·К) и кДж/(кмоль·К) и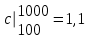 кДж/(кг·К). кДж/(кг·К).Задача № 2. Определить массовую теплоемкость сР генераторного газа при температуре 0 ºС, если его объемный состав 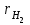 = 18%; = 18%; 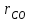 = 24%; = 24%; 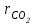 = 6%; = 6%; 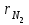 = 52%. Зависимость теплоемкости от температуры не учитывать. = 52%. Зависимость теплоемкости от температуры не учитывать.Решение: Определяем массовый состав генераторного газа 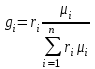 ; ;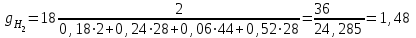 %; %;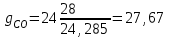 %; %; 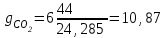 %; %; 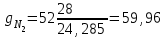 %. %.Массовая теплоемкость отдельных компонентов смеси 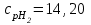 кДж/(кг·К); кДж/(кг·К);  кДж/(кг·К); кДж/(кг·К);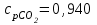 кДж/(кг·К); кДж/(кг·К); 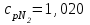 кДж/(кг·К). кДж/(кг·К).Задача № 3. Какое количество теплоты отводится от 1 кг дымовых газов в газоходе котла, если при постоянном давлении температура их понижается от 600 до 200ºС? Объемный состав дымовых газов: СО2 = 11%; О2 = 7% и N2 = 82%. Решение: Определяем массовый состав дымовых газов  %; %;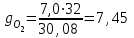 %; %; 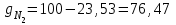 %. %.Средняя массовая теплоемкость отдельных газов в интервале 300-500 ºС определяется по формулам таблицы 4.2: 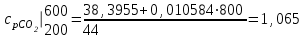 кДж/(кг·К); кДж/(кг·К);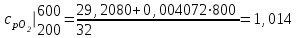 кДж/(кг·К); кДж/(кг·К);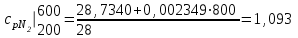 кДж/(кг·К). кДж/(кг·К).Средняя теплоемкость смеси газов в интервале температур 300-500 ºС: 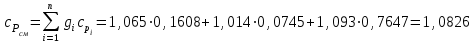 кДж/(кг·К). кДж/(кг·К).Отводимая теплота 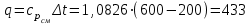 кДж/кг. кДж/кг.Задача № 4. Истинную мольную теплоемкость μcр воздуха при постоянном давлении можно определять по формуле μср = 28,7558 + 0,0057208 t. Получить формулу для определения средней объемной теплоемкости при постоянном объеме 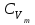 . .Решение: Истинная объемная теплоемкость Ср воздуха определяется по соотношению 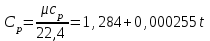 . .Средняя объемная теплоемкость при постоянном давлении 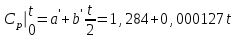 . .Средняя объемная теплоемкость при постоянном объеме 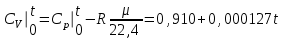 , ,так как для воздуха R = 287 Дж/(кг·К) и μ = 28,96. 4.3 Задания для самостоятельного решения Задание № 1. Определить массовую и объемную теплоемкости воздуха при постоянном давлении и постоянном объеме, считая ее независящей от температуры. Ответ: сV = 0,722 кДж/(кг·К); сP = 1,012 кДж/(кг·К); сV = 0,935 кДж/(м3·К); сР = 1,308 кДж/(м3·К). Задание № 2. Определить массовую теплоемкость кислорода при постоянном объеме и постоянном давлении, пренебрегая зависимостью от температуры. Ответ:сV = 0,655 кДж/(кг·К); сР = 0,916 кДж/(кг·К). Задание № 3. Определить массовую теплоемкость сР при температуре 1000 ºС продуктов сгорания топлива, имеющих объемный состав СО2 = 12,2%; О2 = 7,1%; СО = 0,4% и N2 = 80,3%. Ответ:сР = 1,213 кДж/(кг·К). Задание № 4. Вычислить истинную изобарную теплоемкость воздуха при 800 ºС, принимая линейную зависимость от температуры. Сравнить ее с теплоемкостью, определяемой без учета зависимости от температуры. Какова относительная погрешность определения сР во втором случае? Ответ:1) сР = 1,150 кДж/(кг·К); 2) сР = 1,012 кДж/(кг·К); относительная погрешность σ = 12%. Задание № 5. Определить относительное увеличение изобарной теплоемкости воздуха при нагревании его от t1 = 0ºС до t2 = 1000ºС, принимая зависимость теплоемкости от температуры линейной. Ответ:20 %. Контрольные вопросы: Теплоемкость. Удельная теплоемкость. Истинная теплоемкость. Изобарная теплоемкость. Массовая теплоемкость газовой смеси. Объемная теплоемкость газовой смеси. Практическое занятие № 5 Термодинамические процессы 1.1 Краткие теоретические сведения Изменение состояния тела при взаимодействии его с окружающей средой называется термодинамическим процессом. В общем случае в термодинамическом процессе могут изменяться все три параметра состояния. В технической термодинамике рассматриваются следующие основные термодинамические процессы: изохорный – при постоянном объеме (V = const); изобарный – при постоянном давлении (p = const); изотермический – при постоянной температуре (T = const); адиабатный – без внешнего теплообмена (q = 0); политропный процесс, происходящий при постоянной теплоемкости рабочего тела. Изменение внутренней энергии в термодинамических процессах с идеальным газом Δu = cV (T2 - T1), энтальпия i = u + pV. Изменение энтальпии в любом термодинамическом процессе с идеальным газом Δi = cР (T2 - T1). Изохорный процесс Процесс, протекающий при постоянном объеме, называют изохорным (dv = 0, или v = const). Кривая процесса называется изохорой. При постоянном объеме давление газа изменяется прямо пропорционально абсолютным температурам:  Внешняя работа газа при v = const равна нулю, так как dv = 0. Количество теплоты, участвующее в процессе при постоянной теплоемкости, равно 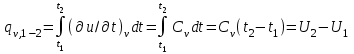 Вся внешняя теплота расходуется только на изменение внутренней энергии тела. При переменной теплоемкости в процессе 1-2 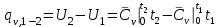 Если процесс 1-2 осуществляется с увеличением давления, то удельное количество теплоты в нем подводится, при этом увеличиваются внутренняя энергия и температура газа. Если давление в процессе понижается, то удельное количество теплоты отводится, уменьшаются внутренняя энергия и температура газа. Изменение энтропии в обратимом изохорном процессе: 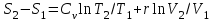 , так как при v = const , так как при v = const  , получим , получим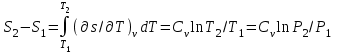 Изобарный процесс Процесс, протекающий при постоянном давлении (dр = 0, или р = соnst), называют изобарным. Кривая процесса называется изобарой. Из уравнения состояния идеального газа при р = соnst находим 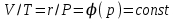 Для процесса 1-2 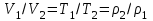 В изобарном процессе объемы одного и того же количества газа изменяются прямо пропорционально абсолютным температурам. При расширении раза его температура возрастает, при сжатии - уменьшается. Удельная работа изменения объема при этом выражается следующим уравнением 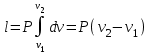 или 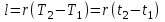 Удельное количество теплоты, сообщенное телу в изобарном процессе, при постоянной теплоемкости равно 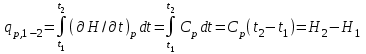 при переменной теплоемкости 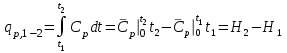 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
