ДЗФКХ07. Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005

Название	Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005
Анкор	ДЗФКХ07.doc
Дата	25.05.2018
Размер	0.71 Mb.
Формат файла
Имя файла	ДЗФКХ07.doc
Тип	Методические указания #19623
страница	5 из 5

1 2 3 4 5

167. Для реакции изомеризации А  В при 25 ⁰С концентрации исходного вещества А в разные моменты времени даны в таблице. Равновесная концентрация вещества А составила С _A_ = 0,078 моль / л. Найти константы скоростей прямой k ₁ и обратной реакций k₂ . Начальная концентрация С _В0 = 0.

t, ч	С _At , моль / л
0	0,366
71,8	0,277
215,8	0,174
333,3	0,130

168. Константа равновесия обратимой реакции А  В равна 10, а константа скорости прямой реакции равна 0,2 с ^{– 1}. Начальные концентрации веществ А и В равны 0,3 моль/л и 0 моль/л соответственно. Определить время, за которое прореагирует 10 % вещества А.

169. Для обратимого процесса А  В известно, что k ₁ + k _{- 1} = 5,13 ^. 10 ^{- 5} c ^{– 1}, а k ₁/ k _{- 1} = 0,575. Начальная концентрация вещества А равна 0,32 моль/л, а вещества В в начальный момент времени нет. Определить концентрации веществ через 100 мин после начала реакции.

170. Для обратимой реакции А  В начальные концентрации составляют С _А0 = 18,23 моль/л и С _{В 0} = 0 моль/л, k ₁ = 0,027 с ^{– 1} . Равновесная концентрация вещества А равна 4,95 моль/л. Определить значение k _{- 1} .

171. Константа скорости прямой реакции А  В при некоторой температуре равна 10, а константа скорости прямой реакции равна 5 ^. 10 ^{- 4}с ^{– 1}. Константа равновесия равна 1,6. В начальный момент присутствует только вещество А. Определить время, за которое прореагирует 30 % вещества А.

172. Константа равновесия обратимой реакции А  В равна 1,4, а константа скорости прямой реакции равна 6 ^. 10 ^{– 5}с ^{– 1}. Определите, какая доля начального количества вещества прореагирует за 40 мин, если в начальный момент в системе содержалось только вещество А.

173. В параллельных реакциях первого порядка: 1. А  В; (k ₁) , 2. А  D. (k ₂) выход вещества В равен 53 %, а время превращения вещества А на 1 / 3 равно 40 с. Найти k ₁ и k ₂.

174. Параллельные элементарные реакции: 1. А  В , 2. 2 А  С характеризуются следующими данными: скорости обеих реакций равны при концентрации вещества А, равной 0,2 моль / л, а при концентрации вещества А равной 0,4 моль / л скорость превращения А составляет 0,24 моль / (л ^. с). Определить значения констант скоростей k₁и k ₂.

175. Параллельные элементарные реакции: 1. А  В, 2. А  С характеризуются следующими данными: выход вещества В равен 63 %, а время полупревращения вещества А по приведенной схеме составляет 19 мин. Рассчитать значения констант скоростей k ₁и k ₂.

176. Определить, сколько азота и оксида азота (I) образуется через 0,1 с при нагревании

4 моль/ л окиси азота при 1300 К, если константы скорости параллельных бимолекулярных реакций равны k ₁= 25,7 и k₂= 18,2 л/(моль ^. с).

 N₂ + O₂ (k ₁)

2 NO

 N₂O + 0,5 O₂ . (k ₂)

177. Реакция разложения вещества А может протекать параллельно по трем направлениям:

1. А  В, 2. А  D, 3. А  F. Концентрации продуктов в смеси через 5 мин после начала реакции были равны: С _B = 2 моль / л, C _D = 1,5 моль / л, C _F = 3 моль / л. Определить константы скорости k₁, k₂, k₃, если период полураспада вещества А равен t _½ = 8 мин.

178. Для некоторой системы, в которой протекают конкурирующие необратимые реакции:

1. А + В ® D ; 2. А + С ® F ; при 25 ⁰ С соотношение продуктов составило C _D : C _F = 1 : 5. При 60 ⁰ С соотношение продуктов составило C _D : C _F = 1 : 3. Определить энергию активации реакции 2, если для первой реакции она составляет 30 кДж / моль.

179. Последовательная реакция А  В  С характеризуется следующими данными: при достижении максимума концентрации вещества В отношение концентраций С _А / С _В = 4 : 5, а время превращения вещества А на 25 % составляет 85 с. Определить значения констант скоростей k ₁и k ₂.

180 . В системе осуществляется последовательная реакция

Максимальная концентрация вещества В равно 0,77 [A] ₀ и достигается через 170 мин после начала реакции. Рассчитать k ₁и k ₂ .

181. Распад радиоактивного изотопа Zn ³⁰ по схеме: Zn ³⁰  Ga ³¹ Ge ³²

характеризуется тем, что максимальное содержание радиоактивного изотопа галлия в образце достигается через 30,3 суток. Причем отношение числа атомов изотопа цинка к числу атомов изотопа галлия в это время оказывается равным 3,48. Определить периоды полураспада изотопов цинка и галлия.

182. Последовательная реакция первого порядка протекает по схеме:

.

При 298 К k₁ = 0,1 мин ^{- 1}; k₂ = 0,05 мин ^{- 1}; начальная концентрация исходного вещества С_A₀= 0,5 моль / л. Вычислить: 1. координаты максимума кривой С _B = f (t); 2. Время достижения концентрации С _A = 0,001 моль / л (продолжительность реакции А  B); 3. концентрации С _B и С _D в момент окончания реакции А  B.

183. Образец радиоактивного урана массой 200 г распадается по схеме:

(над стрелками указаны периоды полураспада). Рассчитать массы нептуния и плутония через 10 мин. После начала распада. Определить максимальную массу нептуния, которая может быть получена из данного образца урана.

184. Образец радиоактивного урана массой 200 г распадается по схеме:

,

где значения констант составляют k₁ = 4,7 ^. 10 ^{– 18} с ^{– 1} и k₂ = 1,381 ^. 10 ^{– 11} с ^{– 1} . Определить периоды полураспада урана и радия и максимальную массу, которая может быть получена из данного образца урана.

185. Был предложен следующий механизм термического разложения озона:

О₃ ® O ₂+ O (k ₁)

O + O₂® O₃(k _{– 1})

O + O₃® 2O₂ (k ₂)

С помощью метода квазистационарных концентраций получить выражение для скорости распада, включающее константы k₁, k _{- 1}, k₂ и концентрации О₂ и О₃.

186. Для реакции NO₂Cl  NO₂ + 0,5 Cl₂ предложен следующий двухстадийный механизм:

1. NO₂Cl  NO₂ + Cl ^. (k ₁ );

2. NO ₂ Cl + Cl ^.  NO ₂ + Cl ₂. (k ₂ )

Используя метод квазистационарных концентраций, вывести уравнение для скорости разложения NO₂Cl.

187. В одной из теорий мономолекулярных реакций был предложен следующий механизм активации молекул (схема Линдемана): 1. А + А  А* + А, (k ₁ ) (активация)

2. А + А*  А + А, (k _{- 1}) (дезактивация)

3. А*  В + D. (k₂) (распад)

Используя метод квазистационарных концентраций, вывести уравнение для скорости мономолекулярной реакции и определить порядок реакции при больших и малых концентрациях А.

188. Предложен следующий механизм для гомогенного пиролиза метана (М - инертная молекула): 1. CH₄ + М® CH₃^. + H ^. + М; (k ₁)

2. CH₄+ CH₃^. ® C₂H₆+ H ^. ; (k ₂)

3. CH₄+ H ^. ® CH₃^. + H₂ ; (k ₃)

4. H ^. + CH₃^. + M ® CH₄+ M. (k ₄)

Вывести уравнение для скорости образования C₂H₆ на основе приведенного механизма, используя метод стационарных концентраций. Концентрации СН₃^ и Н ^ очень малы, поэтому стационарны и не должны входить в уравнение.

189. Химическая реакция N₂O  N₂ + 0,5 O₂ протекает по следующему механизму (М – инертная частица): 1. N₂O + М  N₂О* + М; (k ₁)

2. N₂O *  N₂ + O ^. ; (k ₂)

3. N₂O * + М  N₂О + М; (k ₃)

4. N₂O + О  N₂ + O₂ ; (k ₄)

Считая концентрации N₂O * и О ^. стационарными, найти выражение для скорости распада N₂O.

190. Дана схема цепной реакции: АН  А ^. + Н ^. , (k ₁)

А ^.  В ^. + С, (k ₂)

АН + В ^.  А ^. + D, (k ₃)

А ^. + В ^.  Р . (k ₄)

Используя метод квазистационарных концентраций, вывести уравнение для скорости образования продукта Р.

191. Вывести уравнение для скорости разложения оксида азота (V) по суммарному уравнению 2 N₂O _{5 ( г)}  4 NO_{2 ( г)} + O_{2 ( г)} при следующем механизме реакции (активные промежуточные частицы NO₃ и NO):

1. N₂O₅  NO₂ + NO₃; (k ₁)

2. NO ₂ + NO ₃  N ₂ O ₅ ; (k _{- 1})

3. NO ₂ + NO ₃  N O₂ + O ₂+ NO; (k ₂)

4. NO + N ₂ O ₅  3 NO ₂. (k ₃)

192. При изучении кинетики реакции SiH _{4 (г)}  Si _(т) + 2 H _{2 (г)} был установлен следующий механизм: 1. SiH₄  SiH₂ + 2 H₂; (k ₁)

2. SiH₂  Si + H₂; (k ₂)

3. SiH₂ + H ₂ SiH₄; (k ₃)

Используя метод квазистационарных концентраций, вывести уравнение для скорости разложения SiH₄.

193. Для реакции нитрит - иона с кислородом предложен следующий механизм:

1. NO₂^- + O₂® NO₃^-+ O; (k ₁)

2. NO₂^-+ O ® NO₃^-; (k ₂)

3. O + O ® O₂; (k ₃)

Вывести уравнение для скорости образования иона NO₃^-, используя метод квазистационарных концентраций. Упростить полученное выражение, предполагая, что реакция (3) гораздо медленнее реакции (2).

194. Предложен следующий механизм разложения азотной кислоты:

1. HNO₃® HO + NO₂;

2. HO+NO₂® HNO₃;

3. HO+HNO₃® H₂O + NO₃.

Предположив, что концентрация НО стационарна, вывести выражение для скорости разложения азотной кислоты. Как изменится приведенное выше уравнение, если предположить, что исчезновение NO₂ происходит быстро?

195. Предполагают, что реакция разложения бромметана 2 CH₃Br  C₂H₆ + Br₂ может протекать по следующему механизму: 1. CH₃Br  CH ₃ ^. + Br ^.; (k ₁)

2. СН ₃ ^. + CH₃Br  C₂H₆ + Br ^. ; (k ₂)

3. Br ^. + CH₃Br  СН ₃ ^. + Br₂ ; (k ₃)

4. 2 СН ₃ ^.  C₂H₆ . (k ₄)

Используя метод квазистационарных концентраций, вывести уравнение для скорости образования этана.

196. Термическое разложение углеводорода R ₂ протекает последующему механизму:
1. R ₂  2 R ^.; (k ₁)

2. R ^. + R ₂  P _B + R ^. ; (k ₂)

3. R ^.  P _A + R ^. ; (k ₃)

4. 2 R ^.  P _A + P _B . (k ₄)

Здесь R ₂, P_A , P_B - устойчивые углеводороды, R ^. и R ^. – радикалы. Найти зависимость скорости разложения R ₂ от концентрации R ₂.

197. Дана следующая схема разложения ацетальдегида:

1. СН₃СНО  СН ₃ ^. + СНО ^.; (k ₁)

2. СН₃ ^. + СН ₃ СНО  СН ₄ + СН ₂ СНО ^. ; (k ₂)

3. СН₂СНО ^.  СН ₃ ^. + СО; (k ₃)

4. СН₃ ^. + СН₃ ^.  С₂Н₆ ; (k ₄)

Используя приближение квазистационарных концентраций, вывести выражение для скорости образования метана и скорости расходования ацетальдегида.

198. Предполагают, что реакция образования фосгена СО + Cl₂  СОCl₂ может протекать по следующему механизму: 1. Cl₂ 2 Cl ^. ; (k ₁)

2. 2 Cl ^.  Cl ₂ ; (k ₂)

3. СО + Cl ^.  СОCl ^. ; (k ₃)

4. СОCl ^.  СО + Cl ^. ; (k ₄)

5. СОCl ^.+ Cl ₂  СОCl₂ + Cl ^. . (k ₅)

Используя приближение стационарных концентраций, вывести выражение для скорости образования фосгена.

199. Предполагают, что распад вещества А ₂в растворителе RH протекает по следующему механизму: 1. А ₂ 2 А ^. ;

2. А ^.  Р + В ^. ;

3. В ^. + RH  BH + R ^. ;

4. R ^. + R ^.  R – R.

Используя приближение квазистационарных концентраций, вывести выражение для скорости образования продукта Р.

200. Для реакции синтеза иодоводорода из простых веществ H_{2 (г)}+ I_{2 (г)} ®2HI _(г) предложен следующий механизм: 1. I₂® 2 I^ ; (k ₁)

2. 2I^ ® I₂; (k ₂)

3. 2I^ + H₂® 2HI. (k ₃)

Используя квазиравновесное приближение, вывести уравнение для скорости образования HI.

201. Для реакции 2 NO + O ₂  2 NO₂ предложен следующий механизм:

1. 2 NO  (NO) ₂ ; ( k ₁, k _{– 1})

2. (NO)₂ + O ₂  2 NO₂. (k ₂)

Вывести уравнение для скорости образования NO₂ , предполагая, что первая стадия – быстрая, а вторая – медленная.
7. Поверхностные явления. Адсорбция

Адсорбцией называют самопроизвольное концентрирование веществ на поверхности раздела фаз. Вещество, которое адсорбирует другое вещество, называют адсорбентом. Для обозначения адсорбируемого вещества используют термин адсорбат.

Адсорбция описывается уравнением Гиббса

, (23)

где C – равновесная концентрация адсорбата в объеме,  - поверхностное натяжение. Это уравнение справедливо для всех видов адсорбции.

В случае адсорбции газов уравнение Гиббса (23) приобретает следующий вид:

,

где p – равновесное парциальное давление адсорбата в газовой среде.

Для описания процесса адсорбции применяют также ряд других уравнений. Мономолекулярная адсорбция на однородной поверхности описывается уравнением Ленгмюра

, (24)

где K – константа адсорбционного равновесия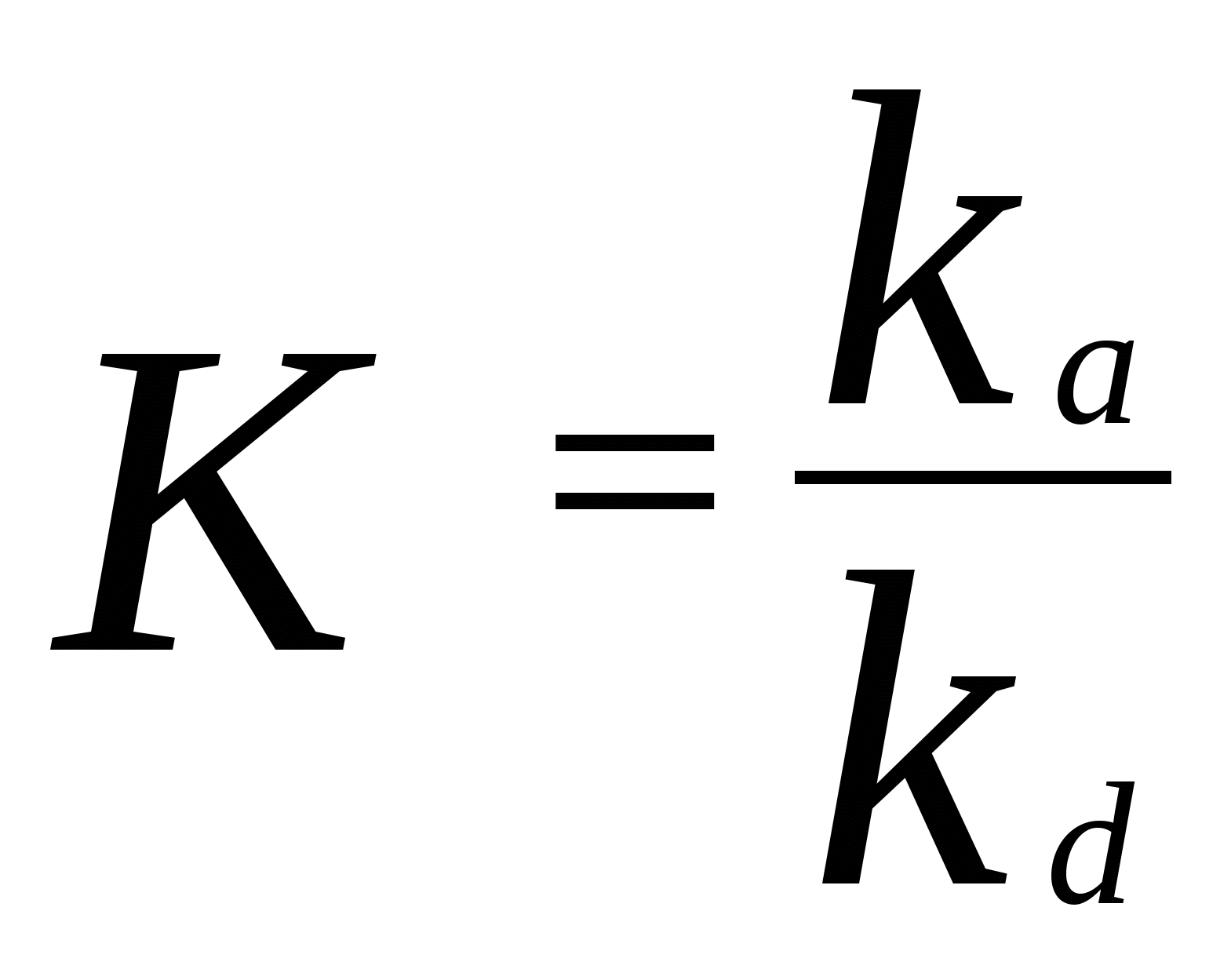

k _a и k _d – константы скоростей адсорбции и десорбции.

Для мономолекулярной адсорбции газов уравнение Ленгмюра (24) имеет вид:

.

Предполагая возможность идеального покрытия поверхности адсорбента мономолекулярным слоем адсорбата, по значениям площади сечения молекул адсорбата S ₀ можно рассчитать предельную адсорбцию a _ :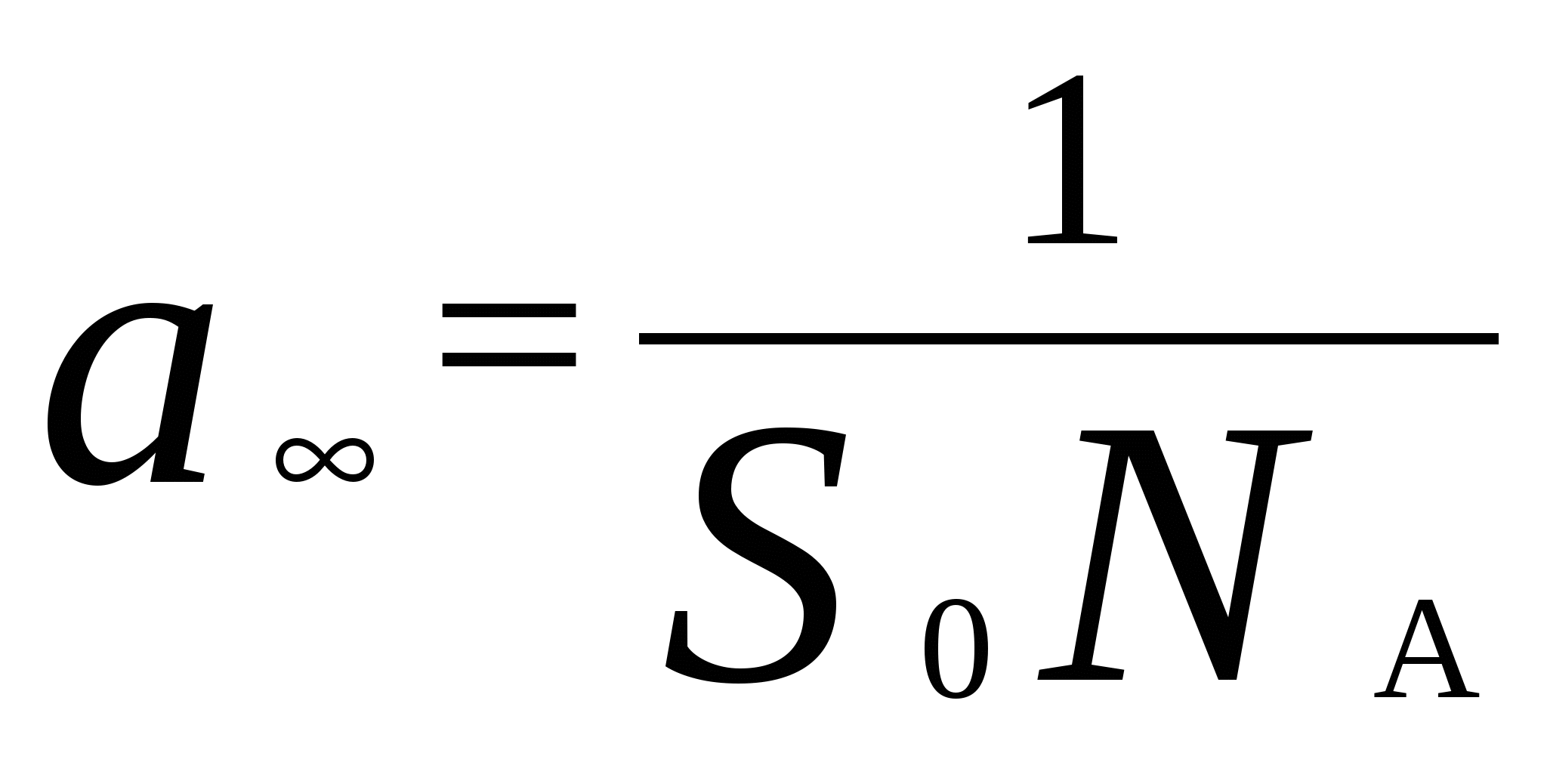

,

где N _A – число Авогадро.

Предельную адсорбцию a_ можно определить по графику зависимости (С / Г) = f(C), полученной преобразованием уравнения изотермы адсорбции Ленгмюра: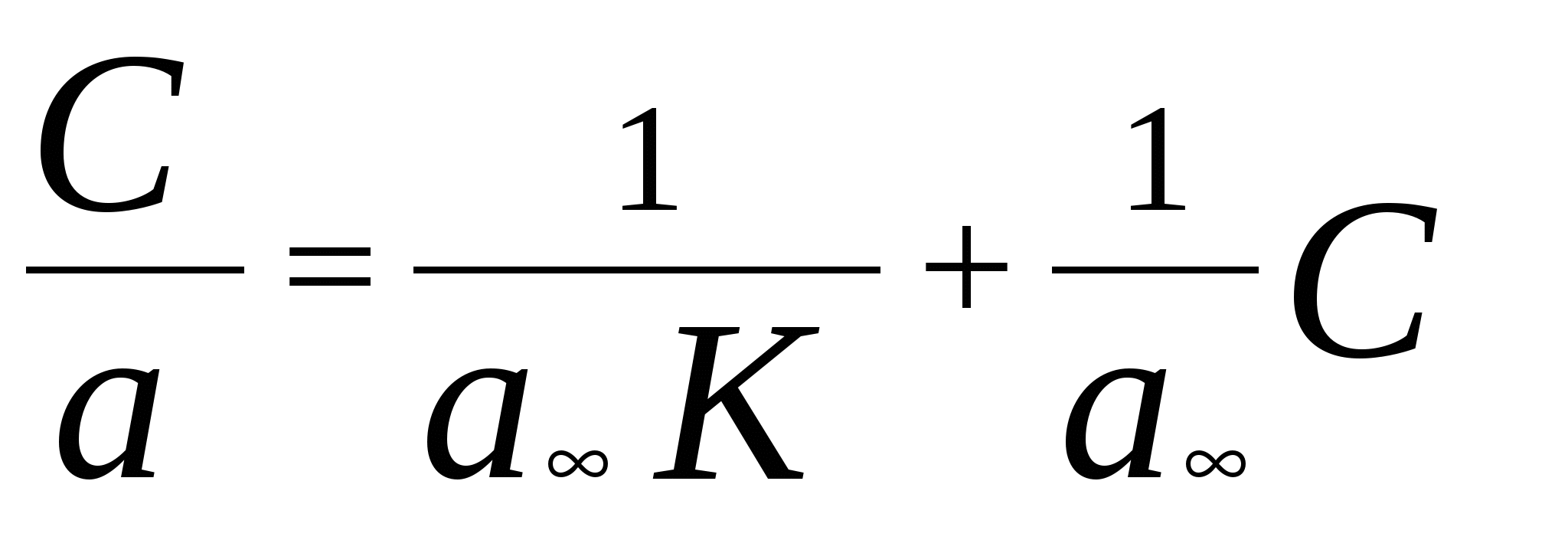

.

Зависимость адсорбции от концентрации адсорбата можно определить с помощью эмпирического уравнения Фрейндлиха

, (25)

где k, n – коэффициенты, определяемые экспериментально. Для этого прологарифмируем уравнение (25):

.

Зависимость lg a - lg C характеризуется прямой линией, тангенс угла которой равен (1 / n), а отрезок, отсекаемый на оси ординат, равен lg k. Для адсорбции газов также справедливо уравнение Фрейндлиха, имеющее вид:

.

Адсорбция на границе жидкость – газ

Адсорбция приводит к изменению поверхностного натяжения жидкости . Вещества, снижающие в результате адсорбции поверхностное натяжение жидкости, называются поверхностно – активными (ПАВ). Вещества, поверхностное натяжение растворов которых по отношению к растворителю увеличивается, называются поверхностно – инактивными (ПИВ).

Способность вещества при адсорбции на границе раздела фаз снижать поверхностное межфазовое натяжение в зависимости от его концентрации в объеме называют поверхностной активностью. Поверхностная активность равна: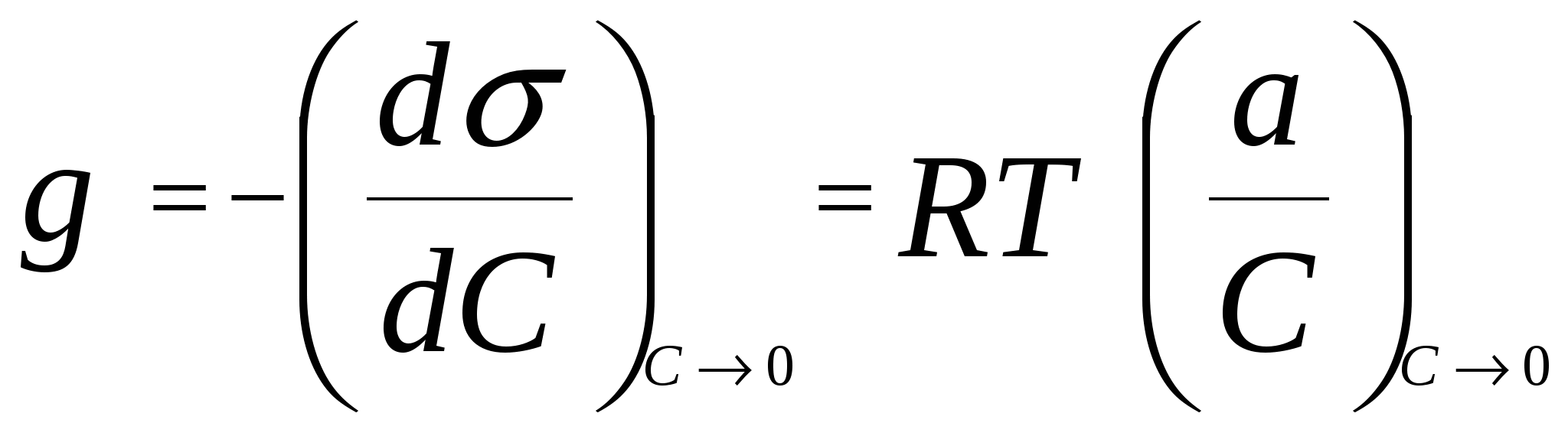

.

В случае адсорбции ПАВ g  0 и (d / dC)  0.

Снижение поверхностного натяжения  в результате адсорбции ПАВ на границе раздела жидкость – газ можно определить при помощи уравнения Шишковского:

, (26)

где A, B – эмпирические коэффициенты.

Пример 20. При Т =298 К поверхностное натяжение (σ) воды равно 72,75 мДж / м²

Для 0,05 М раствора уксусной кислоты поверхностное натяжение равно 71, 2 мДж / м². Рассчитать адсорбцию уксусной кислоты на поверхности раствора.

Решение. Воспользуемся уравнением Гиббса:

.

Заменим производную dσ / dC отношением Δσ / ΔC , так как по условию дано только два значения поверхностного натяжения. Тогда:

g =  (Δ σ / Δ С ) =  (71,2 – 72,75) ^.10 ^{– 3} / 0,05 ^. 10 ³ = 31^. 10 ^{– 6} (Дж ^. м) / моль

После подстановки в уравнение Гиббса получим:

a = 0,05 ^. 10 ³ · 31· 10^{- 6} / 8,314· 298 = 0,626· 10^{- 6} моль / м ²
Пример 21. По приведенным результатам исследования адсорбции пропана на активном угле, проведенного при 20 ⁰С, составьте уравнение изотермы адсорбции Ленгмюра и определите удельную поверхность угля. Площадь сечения молекул пропана принять равной

1,86 ^. 10 ^{– 19} м ².

p (С₃Н₈), Торр	1,0	10,0	50,0	100	400	700
a, моль/кг	0,086	0,673	1,705	2,045	2,568	2,617

Решение. Воспользуемся линейной формой уравнения Ленгмюра в виде: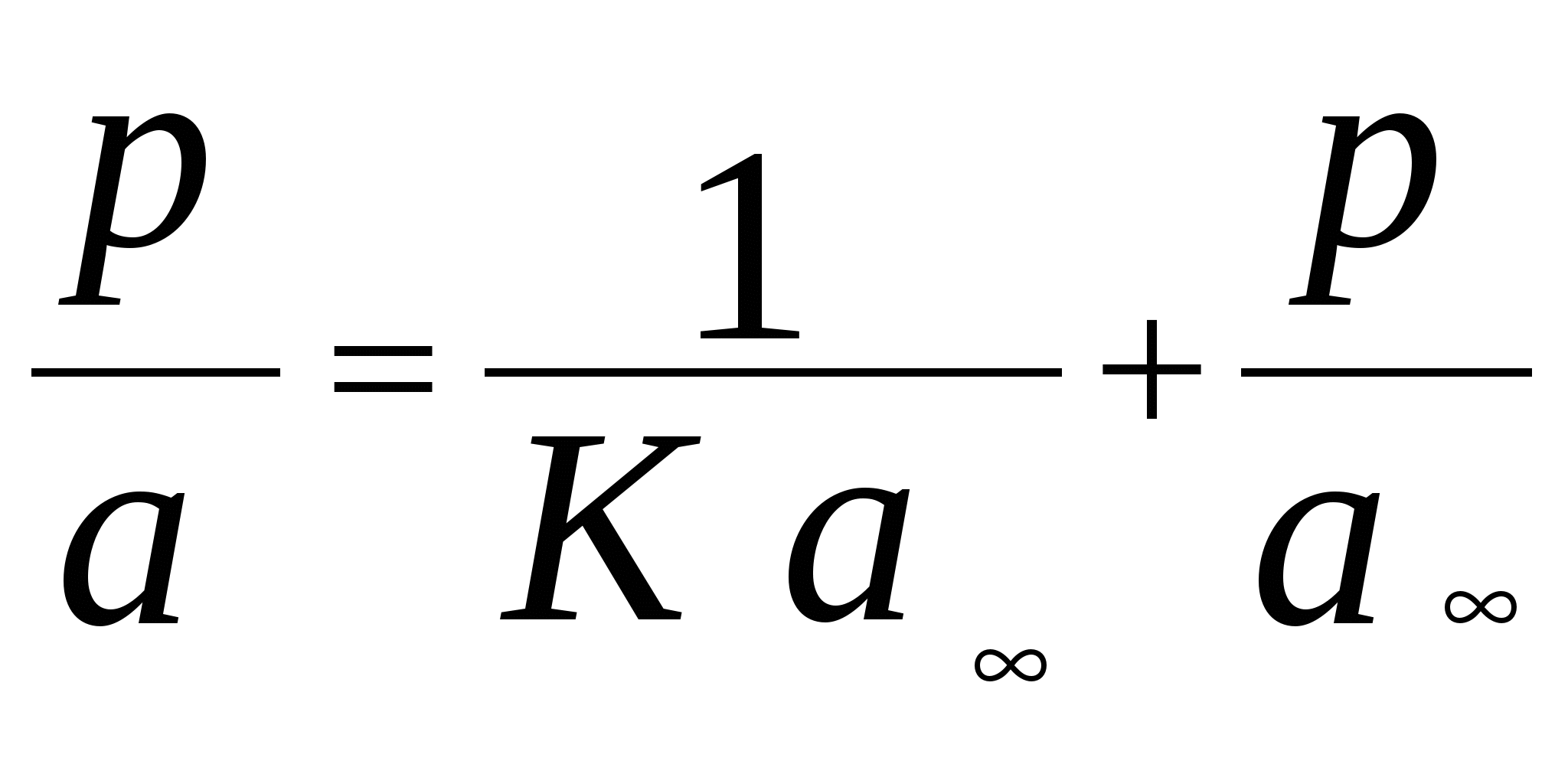

.

Составляем вспомогательную таблицу

p , Торр	1,0	10,0	50,0	100	400	700
p / a, Торр ^.моль ^{– 1} ^. кг	11,628	14,859	29,326	48,900	155,763	267,482

Данные таблицы представим в виде графика p / a = f(p). Угловой коэффициент равен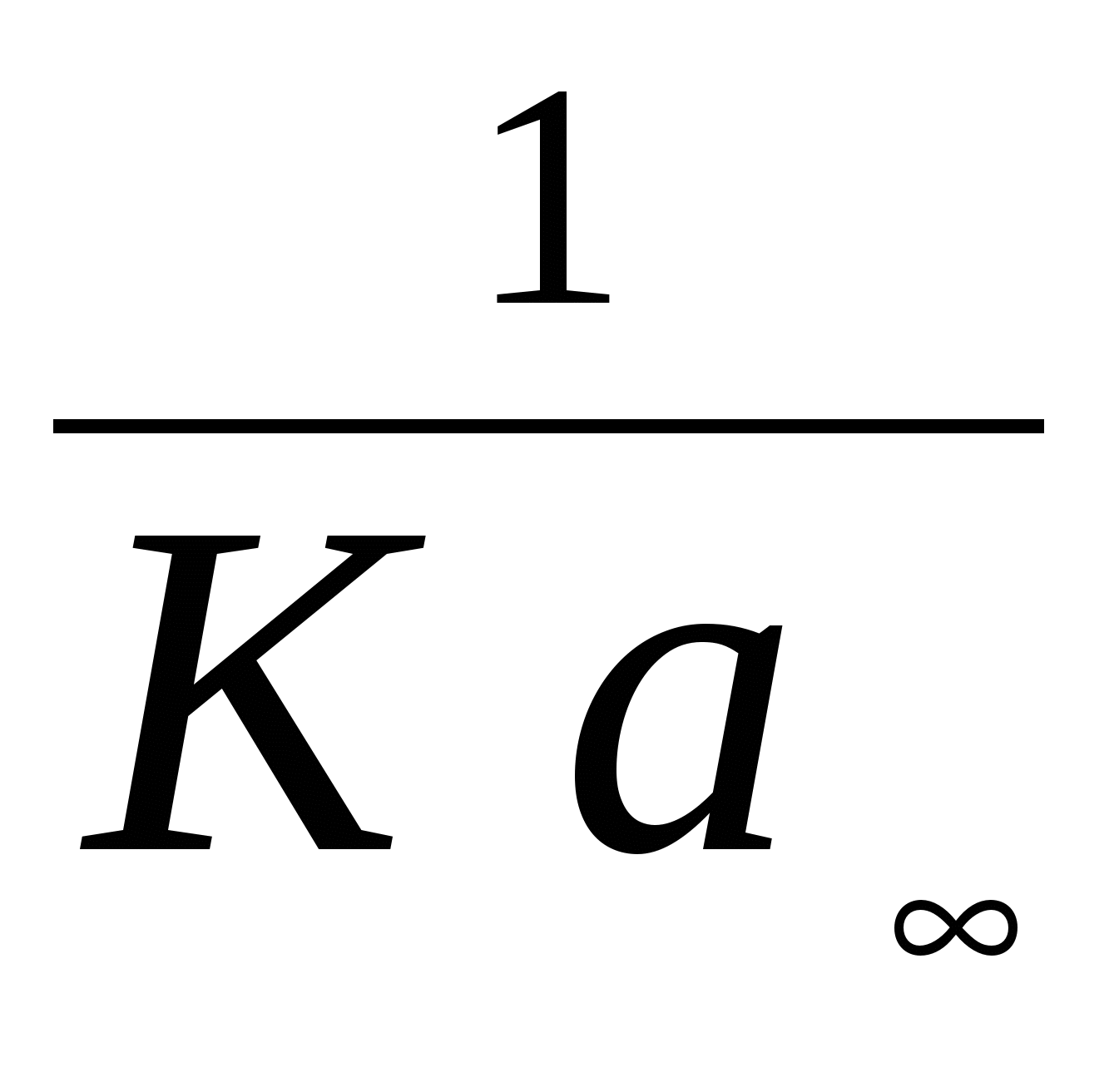

, а по отрезку, отсекаемому на оси ординат, определяется величина

. Получаем следующие результаты:

; b = 0,033.

Более точные значения параметров

и K получаются при статистической обработке данных, например, методом наименьших квадратов. Вычисляем удельную поверхность:

S _уд = a _ S ₀ N _A = 2,74 моль/кг ^. 1,86 ^. 10 ^{– 19} м ^{2 .} 6,022 ^. 10 ²³ моль ^{– 1} = 30,7 ^. 10 ⁴ м ² /кг.

Задачи

202. При изучении адсорбции уксусной кислоты на угле при 25 ⁰С были получены следующие данные:

С, ммоль/ см ³	0,018	0,031	0,062	0,126
a, ммоль/г	0,467	0,624	0,801	1,11

Определить графически константы в уравнении изотермы адсорбции Фрейндлиха.

203. При изучении адсорбции уксусной кислоты на угле при 25 ⁰С были получены следующие данные:

С, ммоль/ см ³	0,268	0,471	0,882
a, ммоль/г	1,55	2,04	2,48

Определить графически константы в уравнении изотермы адсорбции Фрейндлиха.

204. По уравнению Фрейндлиха вычислить равновесную концентрацию уксусной кислоты, если 1 г угля адсорбирует 3,76 ммоль СН₃СООН. Константа k = 2,82; n =2,44.

205. При изучении адсорбции ацетона древесным активированным углем при 20 ⁰С были получены следующие данные:

С, ммоль/л	2,34	14,65	88,62	177,69	268,97
a, ммоль/г	0,208	0,618	1,50	2,08	2,88

Определить графически постоянные уравнения изотермы Фрейндлиха и рассчитать количество ацетона, адсорбируемое 1 г угля при равновесной концентрации ацетона 125 ммоль/л.

206. Определить постоянные уравнения Фрейндлиха, используя следующие данные для адсорбции при 231 К углекислого газа на угле:

р (CO ₂) ^. 10 ^{– 3}, Па	1,00	4,48	10,00	14,40	25,00	45,20
Адсорбция a ^. 10 ², кг/кг	3,23	6,67	9,62	11,72	14,50	17,70

207. По приведенным данным об адсорбции СО₂ на угле марки С при (- 42 ⁰ С) определить константы в уравнении Фрейндлиха.

р (СО₂), Торр	10,0	50,0	100	200	300	400
a, моль/кг	0,659	1,341	1,545	2,000	2,341	2,591

208. По приведенным результатам адсорбции амилового спирта на активном угле марки СКТ при 20 ⁰С составить уравнение изотермы адсорбции Ленгмюра и определить удельную поверхность угля. Площадь поперечного сечения молекул амилового спирта принять равной

1,6 ^. 10 ^{– 19} м ².

С, моль/ м ³	0,94	1,83	3,10	5,60	11,05
a, моль/ кг	0,61	1,21	1,76	2,65	3,96

209. По приведенным данным для адсорбции уксусной кислоты на древесном угле при 25 ⁰С составить уравнение изотермы адсорбции Фрейндлиха.

С, моль / л	0,05	0,10	0,50	1,00	1,50
a, г / г	0,04	0,06	0,12	0,16	0,19

210. По приведенным результатам адсорбции СО₂ на угле марки С при (- 42 ⁰ С) составить уравнение изотермы адсорбции Фрейндлиха.

р (СО ₂), кПа	1,00	4,48	10,0	14,4	25,0	45,2
a ^. 10 ³, моль/ кг	7,34	15,2	21,9	26,6	32,9	40,2

Задачи № 211 - 214. По приведенным данным: а) построить изотерму адсорбции; б) проверить применимость уравнения Ленгмюра; в) если изотерма не соответствует уравнению Ленгмюра, составить уравнение адсорбции Фрейндлиха.

211. Адсорбция H₂S на цеолите CaX при 25 ⁰С:

p (H₂S), Торр	4	6	16	24	50	78	120	154	238
a, моль/кг	0,735	0,882	1,412	1,559	1,941	2,118	2,294	2,471	2,588

212. Адсорбция H₂S на цеолите NaA при 25 ⁰С:

p (H₂S), Торр	6	14	26	50	76	102	152	182	224
a, моль/кг	2,294	2,941	3,235	3,529	3,765	3,882	4,059	4,176	4,298

213. Адсорбция H₂S на цеолите CaА при 25 ⁰С:

p(H₂S), Торр	4	6	12	24	50	76	102	152	224
a, моль/кг	1,588	2,824	3,294	3,765	4,176	4,353	4,471	4,647	4,706

214. Адсорбция H₂S на цеолите NaХ при 25 ⁰С:

p (H₂S), Торр	6	14	24	50	78	120	154	182	234
a, моль/кг	2,824	3,824	4,118	4,471	4,706	4,882	5,000	5,059	5,235

Задачи №№ 215 - 221. Вычислить адсорбцию (a) моль/м² данного вещества по приведенным данным поверхностного натяжения водного раствора и воды ():

№	Вещество	s раствора, мДж / м ²	Концентра ция, моль/л	s (Н₂О), мДж / м ²	Темпера тура, К
215	CH₃-CH₂-COOH Пропионовая кислота	55,6	0,5	71,96	298
216	CH₃-(CH₂)₃-COOH Валерьяновая кислота	52,1	0,5	75,62	273
217	CH₃COOH Уксусная кислота	71,2	0,05	72,75	293
218	CH₃-CH₂-COOH Пропионовая кислота	67,7	0,05	72,75	293
219	NaCl	78,4	1,3	73,6	288
220	NaCl	76,9	2,34	73,6	288
221	CH₃COOH Уксусная кислота	70,9	0,125	73,6	288

Задачи № 222 - 226. При адсорбции указанных газов на активированном угле получены следующие результаты (см. табл.). Вычислить постоянные в уравнении Лэнгмюра для газовой адсорбции.

№	газ	Давление, Па	Количество адсорбированного газа	Т, К
222	Ar	31,9 ^. 10³; 130,5 ^. 10³; 290 ^. 10³	5; 15,4; 24 мг/г	194,7
223	Kr	1,35 ^. 10⁴; 2,63 ^. 10⁴; 3,93 ^. 10⁴	0,15; 0,27; 0,38 моль/г	273
224	CO	6,63 ^. 10⁴; 7,94 ^. 10⁴; 9,25 ^. 10⁴	0,55; 0,62; 0,68 моль/г	273
225	CO₂	4,8 ^. 10^-1; 11,9 ^. 10^-1; 20,6 ^. 10^-1	0,122; 0,195; 0,255 моль/г	298
226	N₂	2,8 ^. 10^-1; 6,1 ^. 10^-1; 17,3 ^. 10^-1;	0,65; 0,75; 0,85 моль/г	293

Задачи № 227 - 229. Построить изотерму поверхностного натяжения, используя значения поверхностных натяжений водных растворов данных веществ при указанной температуре (см.табл.), если поверхностное натяжение воды при 293 К равно 72,75 м Дж / м², а при 298 К – 71,96 м Дж/м ². Определить графически адсорбцию вещества при указанной концентрации.

№	вещество	С _(ПАВ), ммоль/л	s _{ж - г} , м Дж/м²	С _х, ммоль/л	Т, К
227	Додецилсульфат натрия	2,16; 3,96; 6,6; 8,3; 9,3; 9,8; 10,2; 11,2	62; 54; 47; 43; 42; 41; 41; 41	5,0	293
228	Уксусноэтиловый эфир	7,8; 15,6; 31,2; 62,5; 12,5; 250; 500	69,6; 68; 65,8; 61,5; 56,2; 49,7; 41,5	20,0	298
229	Уксусноэтиловый эфир	5,3; 7,4; 19,5; 30,2; 60,7; 120,8;	63; 62,2; 60,1; 54,2; 48,5; 40,3	50,0	293

№ 230. По приведенным результатам массовой адсорбции пентанола на активированном угле при температуре 20°С построить изотерму адсорбции и составить уравнение адсорбции.

С, моль/м ³	0,94	1,83	3,1	5,6	11,05
a, моль/ кг	0,61	1,21	1,76	2,65	3,96

№ 231 - 236. Определить поверхностную активность вещества по указанным данным.

№	Вещество	s , мДж/м²	s (Н₂О), мДж/м ²	Т, (К)	С_.ПАВ, моль/л
231	CH₃-CО-O-C₂H₅ уксусноэтиловый эфир	68	71,96	298	15,6
232	CH₃COOH уксусная кислота	71,2	72,75	293	0,05
233	CH₃-CH₂-COOH пропионовая кислота	67,7	72,75	293	0,05
234	CH₃-CH₂-COOH пропионовая кислота	55,6	71,96	298	0,5
235	CH₃-(CH₂)₃-COOH валерьяновая кислота	52,1	75,62	273	0,5
236	CH₃COOH уксусная кислота	71, 2	72,75	293	0,125

237 - 240. Определить площадь занимаемую молекулой вещества (указанного в табл.) в насыщенном адсорбционном слое активированного угля.

№	Название вещества	a_¥ - предельная адсорбция
237	C₃H₇OH пропанол	5,3 ^. 10 ^{- 10} (моль/см²)
238	CH₃-CH-COOH изомасляная кислота \| CH₃	5,4 ^. 10 ^{- 9} (кмоль/м²)
239	C₆H₅NH₂ анилин	6,01 ^. 10 ^{- 9} (кмоль/м²)
240	C₅H₁₁OH пентанол	5,3 ^.10 ^{– 10} (моль/см²)

ЛИТЕРАТУРА
1. Краткий справочник физико-химических величин / Под. ред. А. А. Равделя и А.М. Пономаревой. Л.: Химия, 1983.

2. Д. Сталл, Э. Вестрам, Г. Зинке. Химическая термодинамика органических соединений. М.: Мир, 1971.

3. Физическая химия т.1, т. 2 / К.С. Краснов, Н.К. Воробьев, И. Н. Годнев и др. М.: Высшая школа, 1995.

4. И.В. Кудряшов, Г.С. Каретников «Сборник примеров и задач по физической химии»,1991, Москва, «Высшая школа».

5. Задачи по физической химии / В. В. Еремин, С. И. Каргов, И. А. Успенская и др. – М.: Изд-во «Экзамен», 2003. – 320 с.

6. Бадаев Ф. З., Батюк В. А. Цепные реакции. Москва, Изд-во МТГУ, 1995.

7. Химическая термодинамика. Методические указания. / Е. Е. Гончаренко, В. А. Батюк, Н. М. Елисеева и др. М.: Изд-во МГТУ, 1994.

Содержание

1. Зависимость термодинамических функций от температуры

2. Фазовое равновесие в однокомпонентных системах

3. Закон распределения. Экстракция

4. Термодинамика растворов неэлектролитов