ДЗФКХ07. Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005

• Название: Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005
• Анкор: ДЗФКХ07.doc
• Дата: 25.05.2018
• Размер: 0.71 Mb.
• Имя файла: ДЗФКХ07.doc
• Тип: Методические указания; #19623
• страница: 3 из 5

4. Термодинамика растворов неэлектролитов

Зависимость между давлением насыщенного пара данного компонента над раствором p_iи его мольной долей x_i устанавливается законом Рауля

,

где p_i - давление насыщенного пара над чистым компонентом. В идеальных растворах закон Рауля выполняется для обоих компонентов во всем интервале составов.

Для бинарного раствора парциальные давления компонентов A и B определяются законом Рауля

Общее давление пара над раствором

,

так как .

Соотношение между составом пара и жидкости в системах, подчиняющихся законам идеальных растворов, может быть выражено через давление насыщенных паров чистых компонентов и общее давление. Согласно закону Рауля и следствию из закона Дальтона

.

Отсюда следует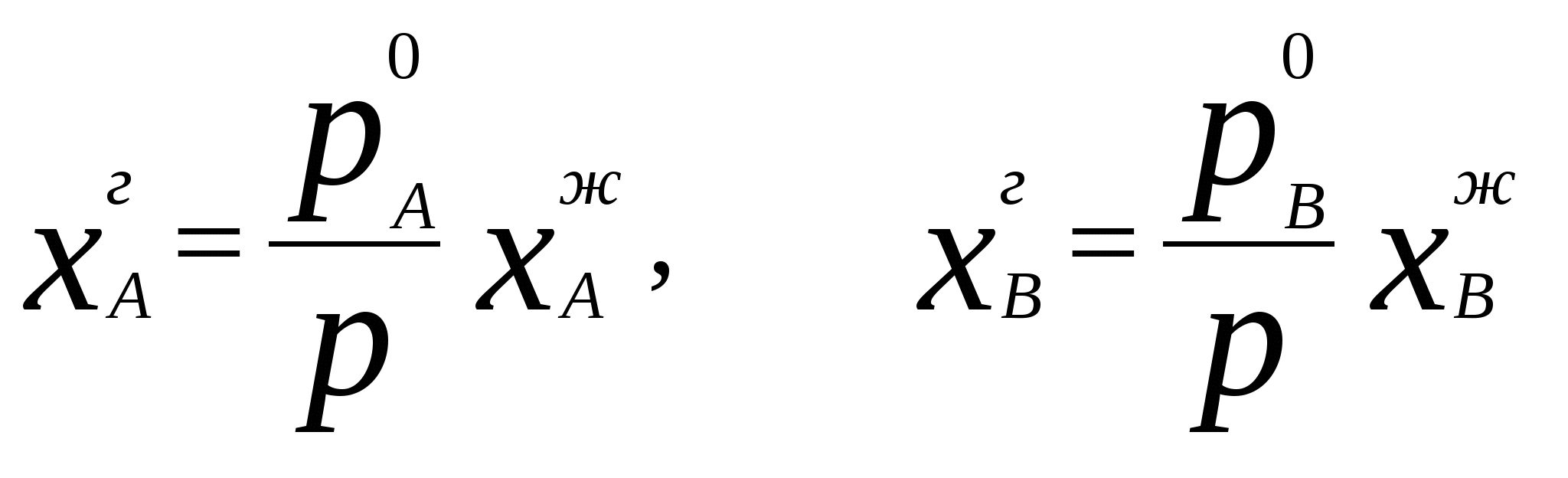

.

В реальных предельно разбавленных растворах для растворителя выполняется закон Рауля, а для растворенного вещества выполняется закон Генри:

,

где K _Г - константа Генри.

Парциальные молярные величины

Парциальной молярной величиной (пмв) данного компонента называют частную производную от экстенсивного свойства раствора (g) по числу моль этого компонента

(n_i ) при постоянстве температуры, давления и числа моль всех остальных компонентов: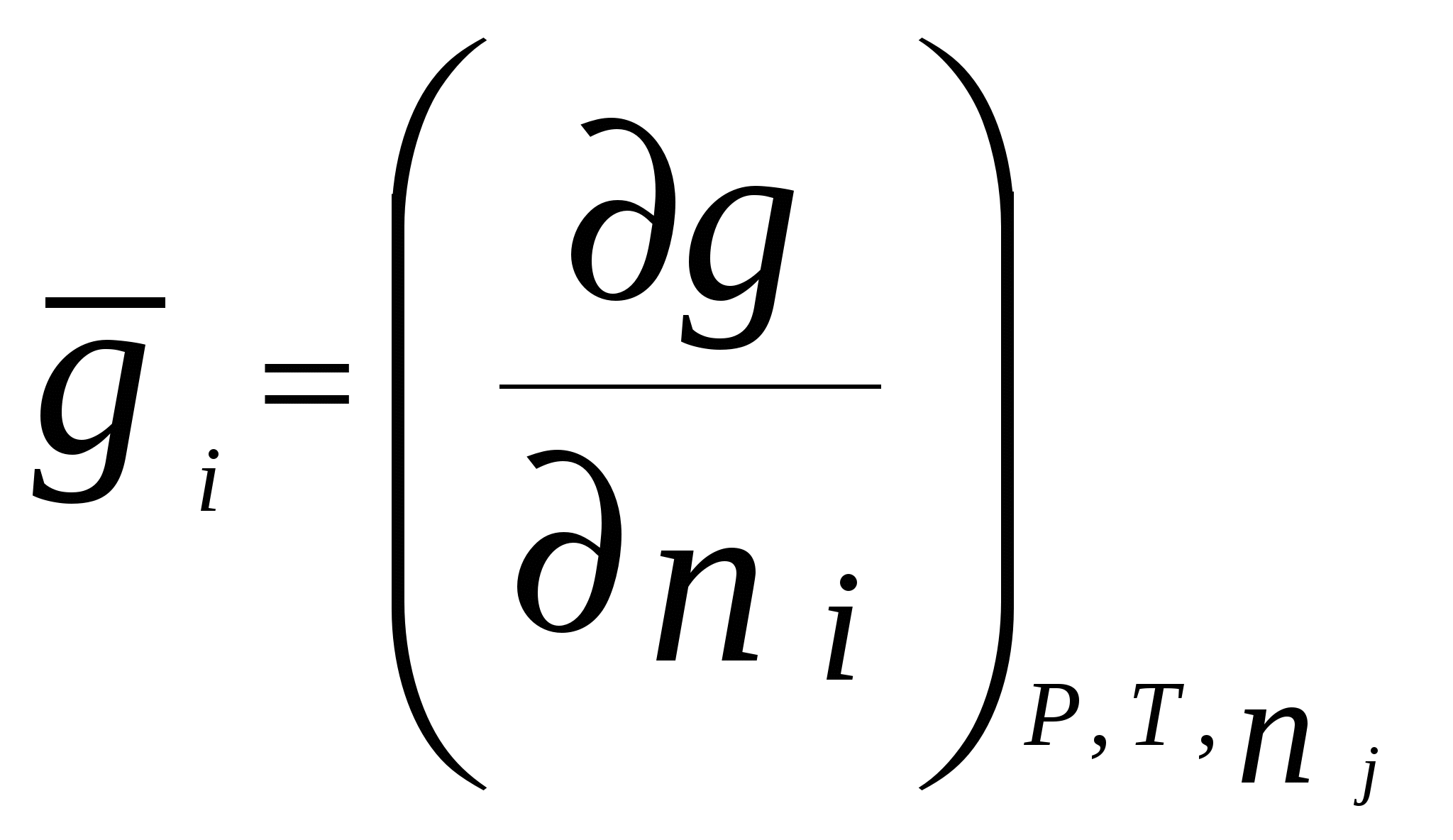

.

Парциальная молярная величина () i- го компонента характеризует изменение данного экстенсивного свойства раствора (g) при добавлении 1 моль i – го компонента к столь большому количеству раствора при постоянных Т и p, что добавление этого количества компонента практически не изменяет состава раствора.

Общее значение свойства g выражается суммой вкладов всех компонентов (первое уравнение Гиббса  Дюгема):

.

Парциальные молярные величины при постоянных р и Т связаны вторым уравнением Гиббса  Дюгема:


Химический потенциал. Активность. Коэффициент активности

Химический потенциал i - го компонента для идеальных растворов определяется уравнением: ,

где x_i – молярная доля i- го компонента; _i(T) – химический потенциал чистого компонента при р =1,013^.10⁵ Па и x_i = 1. В случае реального раствора

,

где a_i – активность i- го компонента. Активность данного компонента в реальном растворе определяется уравнением: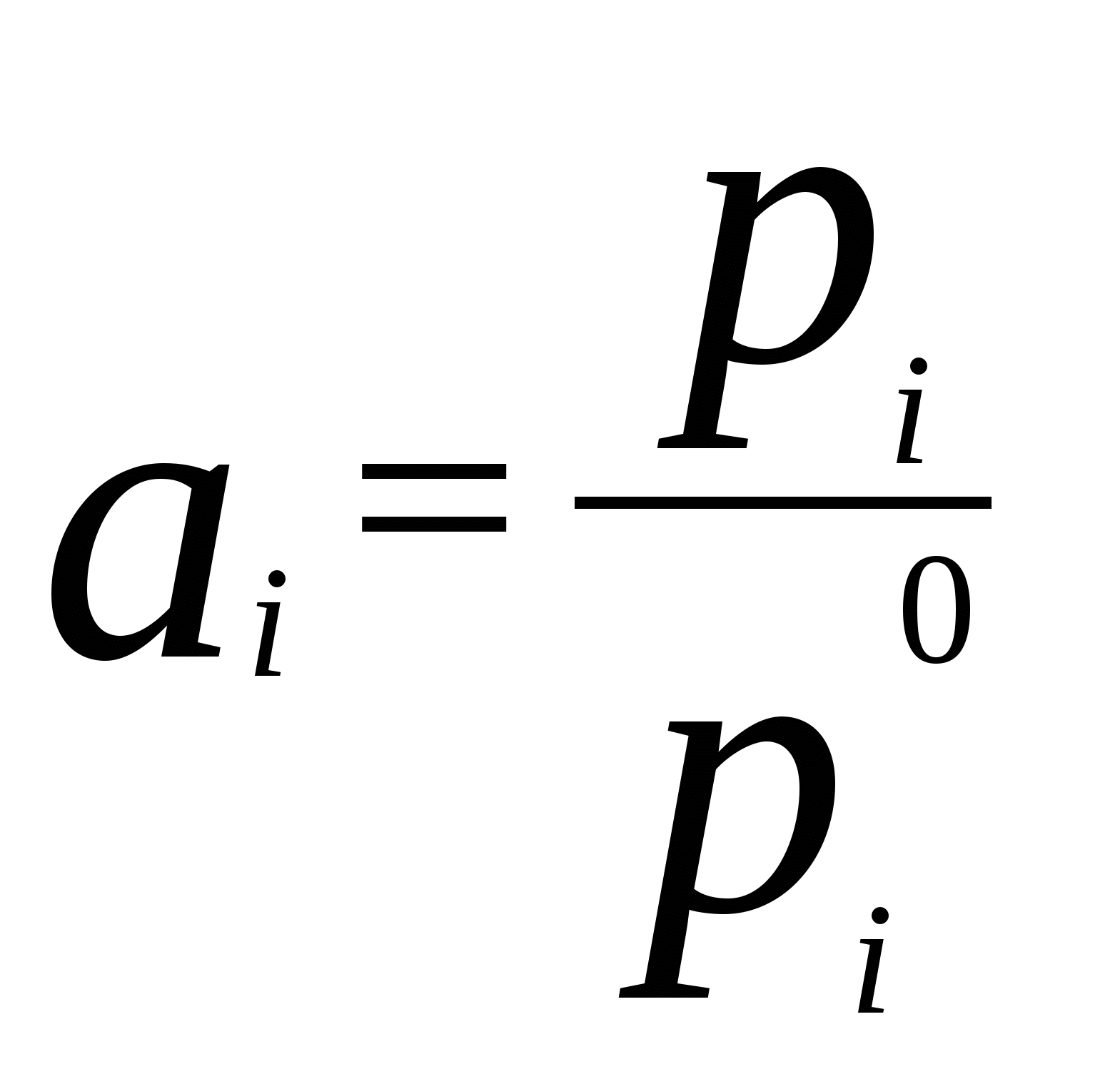

,

где p_i - давление насыщенного пара над чистым компонентом. Коэффициент активности  _i равен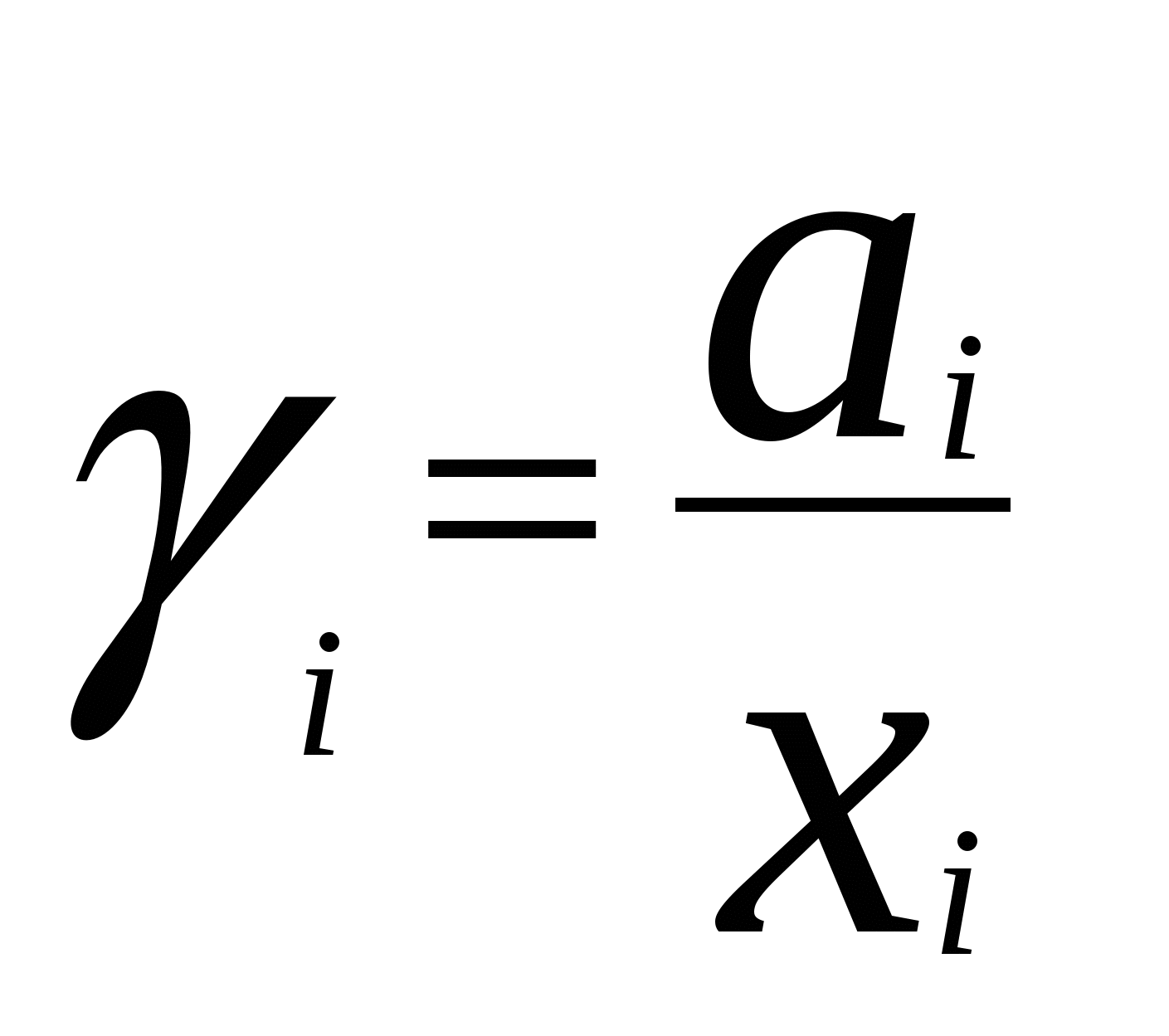

,

где x_i – мольная доля i - го компонента.

Коллигативные свойства растворов

Свойства разбавленных растворов, зависящие только от количества нелетучего растворенного вещества, называются коллигативными свойствами. К ним относятся: понижение давления пара над раствором, повышение температуры кипения и понижение температуры замерзания раствора по сравнению с чистым растворителем, осмотическое давление.

Повышение температуры кипения разбавленного раствора, содержащего нелетучее растворенное вещество, пропорционально моляльной концентрации этого вещества m:

,

где K_Э- эбулиоскопическая константа растворителя: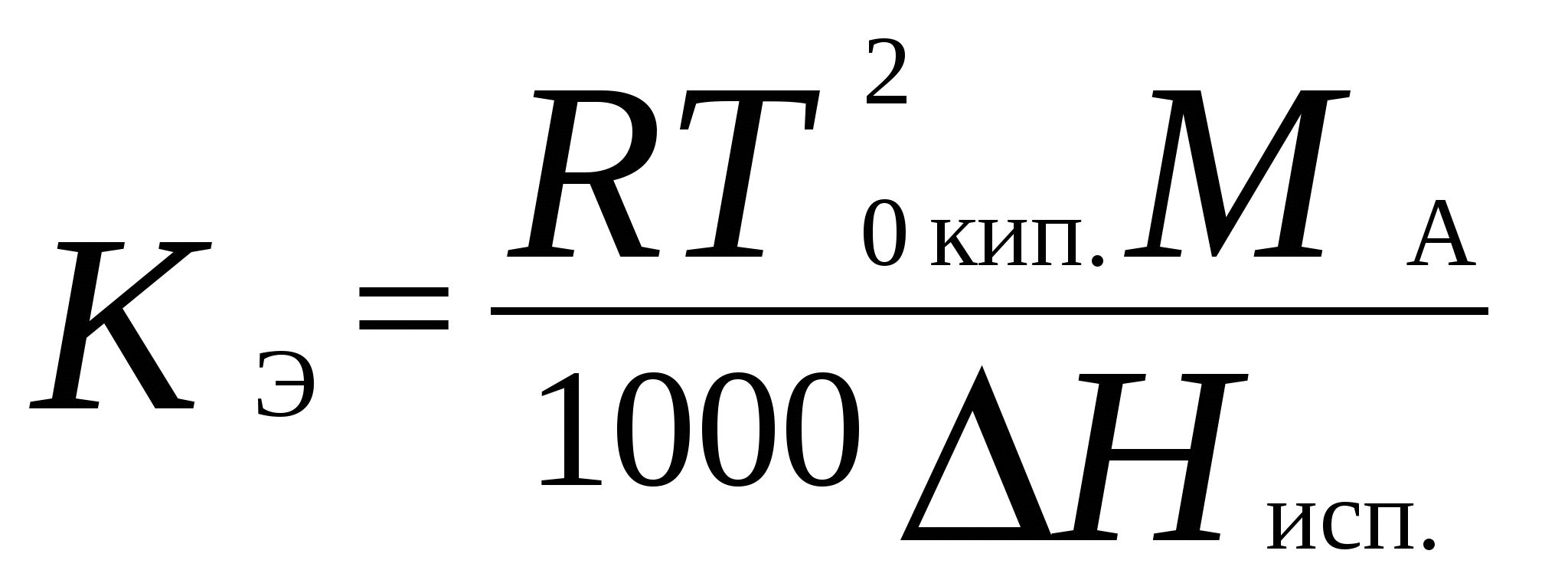

,

Т_{0 кип.} – температура кипения чистого растворителя, M _A – молярная масса растворителя.

Для понижения температуры кристаллизации раствора справедливо следующее соотношение:

,

где K_К– криоскопическая константа растворителя: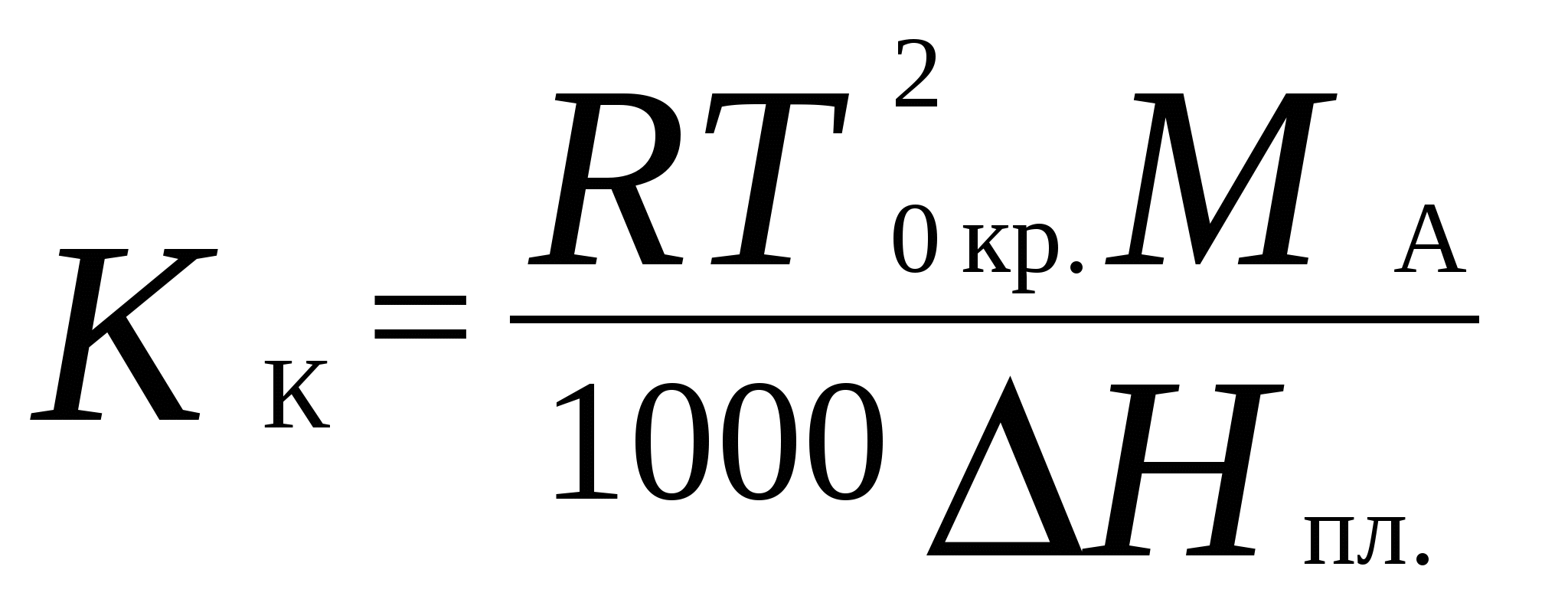

,

Т _{0 кр.} – температура кристаллизации чистого растворителя.

Осмотическое давление  в разбавленных растворах можно рассчитать по уравнению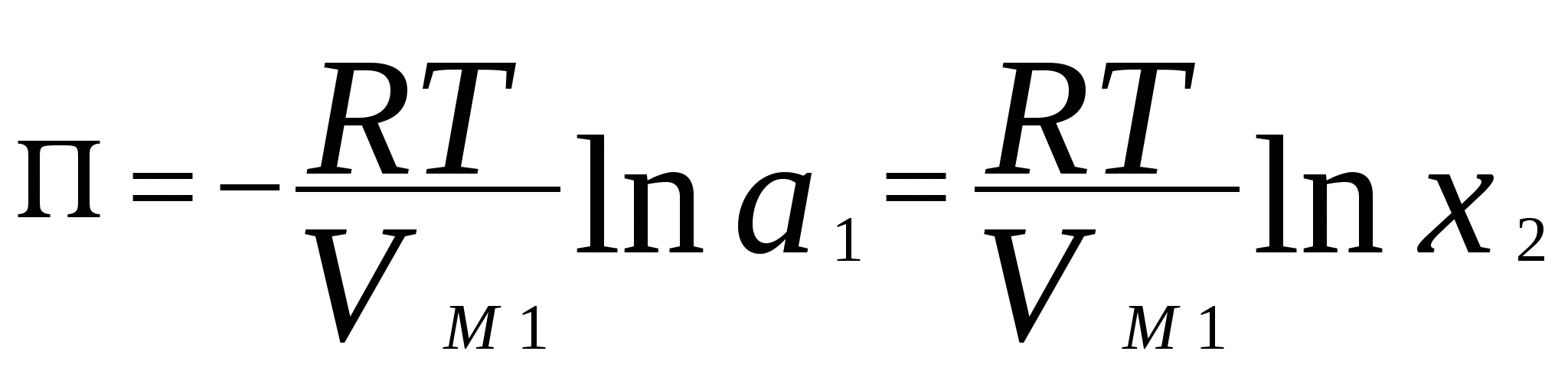

,

где a ₁ - активность растворителя, x ₂ - молярная доля растворенного вещества, V _{M 1} - молярный объем растворителя. Для очень разбавленных растворов это уравнение преобразуется в уравнение Вант-Гоффа:

 = C R T ,

где С – молярная концентрация растворенного вещества.

Пример 10. Рассчитать состав раствора бензол – толуол в молярных долях, который при нормальном давлении кипит при температуре 100⁰С, а также состав образующегося пара. Раствор считать идеальным. Давления паров чистых бензола и толуола при 100⁰ С равны 179,987кПа и 74,126кПа соответственно.

Решение. Находим молярную долю бензола в растворе по закону Рауля:

p = p ⁰₂ + (p ⁰₁ – p ⁰₂ ) x ₁ ,

где p - общее давление пара над раствором

101,32 = 74,126 + (179,987 – 74,126) x ₁ , откуда x ₁ = 0,257 .

Молярная доля толуола в растворе равна x₂ = 1 – x₁ = 0,743 .

Молярная доля бензола в паре равна:

y ₁ = p ₁/ p = x ₁ p ⁰₁ / p = 0,257 . 179,987 / 101,32 = 0,456 .

Вычислим молярную долю толуола в паре: y ₂ =1 – y ₁ = 0,544 .

Пример 11. Плотность 20% водного раствора этилового спирта равна 0,97 г/см³ при

Т = 298 К. Рассчитать парциальный молярный объем этилового спирта, если парциальный молярный объем воды равен 17,4 см³ / моль.

Решение. Находим число моль воды и этилового спирта в 100 г раствора:

n₁= 80 / 18 = 4,44 , n₂ = 20 /46 = 0,43 .

ρ = m /V =100 / V , где V – объем раствора, откуда V =100 / 0,97 =103,09 см³ .

Так как V = n₁V₁ + n ₂ V₂ , находим парциальный мольный объем этилового спирта:

103,09 = 4,44 ^. 17,04 + 0,43 V₂ .

Откуда, V₂ = 60,07 cм³ .

Пример 12. 1) Вычислить активность и рациональный коэффициент активности ацетона С₃Н₆О в водном растворе, если x (С₃Н₆О) = 0,318; p (С₃Н₆О) = 152 Торр; p ⁰ (С₃Н₆О) =

= 229 Торр. 2) Рассчитать химический потенциал μ (С₃Н₆О) , а также изменение химического потенциала Δ μ (С₃Н₆О) при растворении ацетона в воде.

Решение. a (С₃Н₆О) = p / p ⁰ = 152 /229 = 0,664;

Так как a (С₃Н₆О) = x^. γ , γ (С₃Н₆О) = a / x ; γ(с₃н₆о) = 0,664 / 0,318 = 2,09 .

Так как γ больше единицы, отклонения от закона Рауля положительные.

2)Δ μ (С₃Н₆О) = RTln a (С₃Н₆О) = 8,31• 298• (ln 0,664) ^. 10 ^{– 3} = - 1,014 кДж / моль .

Так как μ ⁰ (С₃Н₆О) = Δ _f G ⁰₂₉₈ (С₃Н₆О) = - 155,50 кДж / моль,

μ (С₃Н₆О) = Δ μ (С₃Н₆О) + μ⁰ (С₃Н₆О) = - 1,014 + (- 155,50) = - 156,514 кДж / моль .
Задачи

88. Парциальные молярные объемы воды и метанола в растворе с молярной долей метанола 0,4 равны 17,35 и 39,01 см ³ / моль соответственно. Рассчитать объем раствора, содержащего 0,4 моль метанола и 0,6 моль воды, а также объем до смешения. Плотности воды и метанола равны 0,998 и 0,791 г / см ³ .

89. Парциальные молярные объемы воды и этанола в растворе с молярной долей этанола 0,2 равны 17,9 и 55,0 см ³ / моль соответственно. Рассчитать объемы воды и этанола, необходимые для приготовления 1 л такого раствора. Плотности воды и метанола равны 0,998 и

0,789 г / см ³ .

90. Парциальные молярные объемы ацетона и хлороформа в растворе с молярной долей хлороформа 0,47 равны 74,17 и 80,24 см ³ / моль соответственно. Рассчитать объем такого раствора, имеющего массу 1 кг.

91. Плотность 50 % (масс.) раствора этанола в воде при 25 ⁰ С равна 0,914 г / см ³ . Рассчитать парциальный молярный объем этанола в этом растворе, если парциальный молярный объем воды равен 17,4 см ³ / моль.

92. Раствор, содержащий 60 % (масс.) метанола в воде, имеет плотность 0,895 г /см³ при

20 ⁰ С. Парциальный молярный объем воды в растворе этого состава равен 16,8 см ³. Рассчитать парциальный молярный объем метанола.

93. Парциальные молярные объемы воды и метанола в растворе с молярной долей метанола 0,4 равны 17,35 и 39,01 см ³ / моль соответственно. Рассчитать объемы воды и метанола, необходимые для приготовления 300 мл такого раствора. Плотности воды и метанола равны 0,998 и 0,791 г / см ³ .

94. Давления пара чистых СНCl ₃ и CCl ₄ при 25 ⁰ С равны 26,54 и 15,27 кПа. Предполагая, что они образуют идеальный раствор, рассчитать давление пара и состав (в молярных долях) пара над раствором, состоящим из 1 моль СНCl ₃ и 1 моль CCl ₄.

95. При 80 ⁰ С давление пара дибромэтилена равно 22,9 кПа, а дибромпропилена 16,9 кПа. Считая, что дибромэтилен и дибромпропилен при смешении образуют идеальные растворы, рассчитайте состав пара, находящегося в равновесии с раствором, молярная доля дибромэтилена в котором равна 0,75. Рассчитать состав раствора, находящегося в равновесии с паром, мольная доля дибромэтилена в котором равна 0,50.

96. При 20 ⁰ С давление пара этанола равно 5,93 кПа, а метанола - 11,83 кПа. Считая, что этанол и метанол при смешении образуют идеальные растворы, рассчитайте давление пара раствора, состоящего из 100 г этанола и 100 г метанола, а также состав (в молярных долях) пара над этим раствором при 20 ⁰ С.

97. Давление пара чистых бензола и толуола при 60 ⁰ С равны 51,3 и 18,5 кПа соответственно. Определите при каком давлении при 60 ⁰ С закипит раствор, состоящий из 1 моль бензола и 2 моль толуола. Определите состав пара (в молярных долях).

98. При 90 ⁰ С давление насыщенного пара толуола равно 53328,93 Па, а о – ксилола – 19998,35 Па. Считая этот раствор идеальным, определите состав жидкой смеси в молярных долях, которая будет кипеть при 90 ⁰ С, если давление насыщенного пара смеси при этом равно 50662,5 Па. Определите состав образующегося пара (в молярных долях).

99. При 60 ⁰ С давление насыщенного пара этанола равно 47022,8 Па, а давление насыщенного пара метанола – 83326,5 Па. Смесь этих спиртов, которую можно считать идеальной, содержит 50 % (масс.) каждого компонента. Определите состав пара над этим раствором при 60 ⁰ С.

100. Давление насыщенного пара над хлористым метилом при 273 К равно 2,64 ^. 10 ⁵ Па, а над хлористым этилом при той же температуре – 0,638 ^. 10 ⁵ Па. Считая, что раствор хлористого этила в хлористом метиле подчиняется закону Рауля, определите состав пара (в молярных долях) над 50 % (масс.) раствором.

101. Давление пара чистых хлорбензола и бромбензола при 140 ⁰ С равны 1,237 ^. 10 ⁵ кПа и 0,658 ^. 10 ⁵ Па соответственно. Рассчитайте состав раствора хлорбензол – бромбензол, который при давлении 10 ⁵ Па кипит при температуре 140 ⁰ С, а также состав образующегося пара.

102. Бензол и толуол образуют растворы, близкие по свойствам к идеальному. При

Т = 293 К давления паров бензола и толуола равны соответственно 1,020 ^. 10 ⁴ Па и

0,327 ^. 10 ⁴ Па. Построить график зависимости содержания бензола в паре от содержания бензола в жидкой фазе. Определить содержание бензола в паре, если в жидкой фазе его содержится 40%.

103. Приняв, что SnCl₄ и CCl₄ образуют идеальный раствор, определить изменения энтропии и энергии Гиббса при образовании 0,5 кг раствора, в котором молярные доли компонентов равны 0,5 при Т = 298 К.

104. Давления паров веществ А и В соответственно равны 0,45 ^. 10 ⁵ Па и 1,013 ^. 10 ⁵ Па. Определить состав пара над раствором, полученным смешением 0,5 моль А и 0,7 моль В, если компоненты образуют идеальный раствор.

105. Константа Генри для СО ₂ в воде при 25 ⁰ С равна 1666,4 ^. 10 ⁵ Па. Рассчитайте растворимость (в единицах моляльности) СО ₂ в воде при 25 ⁰ С, если парциальное давление СО ₂ над водой равно 0,1 атм.

106. Константы Генри для кислорода и азота в воде при 25 ⁰ С равны 4,40 ^. 10 ⁹ и

8,68 ^. 10 ⁹ Па соответственно. Рассчитайте концентрации (в моляльностях) растворенных в воде кислорода и азота при 25 ⁰ С, если содержание в воздухе над водой азота 78,2 % и кислорода 20,9 % по объему, а его давление равно 10 ⁵ Па.

107. Бензол и толуол образуют растворы, близкие по свойствам к идеальному. Давление пара чистых бензола и толуола при 60 ⁰ С равны 51,3 и 18,5 кПа соответственно. Построить график зависимости содержания бензола в паре от содержания бензола в жидкой фазе. Определить содержание бензола в паре, если в жидкой фазе его содержится 30%.

108. Хлороформ СНCl ₃ и тетрахлорид углерода CCl ₄ образуют растворы, близкие по свойствам к идеальному. Давления пара чистых СНCl ₃ и CCl ₄ при 25 ⁰ С равны 26,54 и 15,27 кПа соответственно. Построить график зависимости содержания хлороформа в паре от содержания хлороформа в жидкой фазе. Определить содержание хлороформа в паре, если в жидкой фазе его содержится 40%.

109. Этанол и метанол образуют растворы, близкие по свойствам к идеальному. При 20 ⁰ С давление пара этанола равно 5,93 кПа, а метанола - 11,83 кПа. Построить график зависимости содержания этанола в паре от содержания этанола в жидкой фазе. Определить содержание этанола в паре, если в жидкой фазе его содержится 60 %.

110. Дибромэтилен и дибромпропилен образуют растворы, близкие по свойствам к идеальному. При 80 ⁰ С давление пара дибпромэтилена равно 22,9 кПа, а дибромпропилена

16,9 кПа. Построить график зависимости содержания дибромэтилена в паре от содержания дибромэтилена в жидкой фазе. Определить содержание дибромэтилена в паре, если в жидкой фазе его молярная доля 0,45.

111. Давления паров веществ А и В соответственно равны 0,45 ^. 10 ⁵ Па и 1,013 ^. 10 ⁵ Па. Определить состав пара над раствором, полученным смешением 0,3 моль А и 0,5 моль В, если компоненты образуют идеальный раствор.

112. При Т = 308 К давление пара ацетона 0,459 ^. 10 ⁵ Па, а давление пара хлороформа

0,391 ^. 10 ⁵ Па. Над раствором, содержащим 36 % хлороформа, парциальное давление паров ацетона равно 0,2677 ^. 10 ⁵ Па, а хлороформа 0,0964 ^. 10 ⁵ Па. Определить активности компонентов, а также коэффициенты активности.

113. Рассчитать активности и рациональные коэффициенты активности компонентов в растворе вода (1) – пропанол-1 (2), в котором мольная доля пропанола равна x ₂ = 0,3, парциальные давления компонентов над раствором равны:p (H₂O) = 3,84 ^. 10 ³ Па, p(C₃H₇OH) =

= 2,53 ^.10 ³ Па. Давления паров над чистыми компонентами равны:p ⁰(H₂O) = 4,24 ^. 10 ³ Па;

p ⁰(C₃H₇OH) = 3,8 ^.10 ³ Па. Вычислить изменение химического потенциала и химический потенциал при растворении компонента 2 в компоненте 1 (₂ -  ₂⁰). При расчете принять, что

 ⁰ =  _f G ⁰ ₂₉₈ (чистого компонента). Недостающие данные взять из справочника.

114. При температуре 57,2 ⁰ С и давлении 1 атм молярная доля ацетона в паре над раствором ацетон – метанол с молярной долей ацетона в растворе x _A = 0,400 равна y_A = 0,516. Рассчитать активности и рациональные коэффициенты активности обоих компонентов в этом растворе, используя закон Рауля. Давления паров чистых ацетона и метанола при этой температуре равны 756 и 551 Торр соответственно.

115. Для раствора этанол – хлороформ при 35 ⁰ С получены следующие данные:

x этанола (р-р)	0	0,2	0,4	0,6	0,8	1,0
y этанола (пар)	0	0,1382	0,1864	0,2554	0,4246	1,0000
pобщее, кПа	39,345	40,559	38,690	34,387	25,357	13,703

Рассчитать коэффициенты активности обоих компонентов, используя закон Рауля.

116. Для раствора сероуглерод – ацетон при 35,2 ⁰ С получены следующие данные:

x (CS2 )(р-р)	0	0,2	0,4	0,6	0,8	1,0
p (CS2), кПа	0	37,3	50,4	56,7	61,3	68,3
p ацетона, кПа	45,9	38,7	34,0	30,7	25,3	0

Рассчитать коэффициенты активности обоих компонентов, используя закон Рауля.

117. Экспериментально определены значения парциальных давлений над системой ацетон  хлороформ при Т = 308,2 К в зависимости от состава:

x (CHCl 3)	0	0,2	0,4	0,6	0,8	1,0
p (CHCl 3) . 10 – 4 Па	0	0,453	1,093	1,973	3,00	3,906
p [(CH3)2 CO] . 10 – 4 Па	4,586	3,600	2,440	1,360	0,560	0

На основании этих данных построить график зависимости парциальных и общего давлений над системой от состава. Сравнить с графиком для идеальной системы. Определить, при каком общем давлении закипит смесь, содержащая 50% хлороформа при Т = 308,2 К. Найти состав смеси, которая будет кипеть при p = 3,5 ^. 10 ⁴ Па.

118. Температура кипения чистого бензола 353,1 К. Удельная теплота испарения при температуре кипения равна 399,69 кДж/кг. Раствор содержащий 0,0128 кг нафталина в 1 кг бензола. Определить: а) температуру кипения этого раствора; б) давление пара бензола над этим раствором, если давление насыщенного пара над чистым бензолом равно 2,433 ^. 10 ⁴ Па.

119. Водный раствор, содержащий нелетучее растворенное вещество, кристаллизуется при 271,5 К. Определить температуру кипения раствора и давление пара над раствором при 298 К. Криоскопическая константа воды равна 1,86, эбулиоскопическая – 0,513. Давление насыщенного пара над чистой водой при 298 К равно 3167,21 Па.

120. При растворении 0,006 кг некоторого вещества в 0,25 кг воды температура кипения повысилась на 0,204 К . При растворении 0,003 кг этого вещества в 0,2 кг бензола температура кипения повысилась на 0,668 K. Найти эбулиоскопическую константу бензола, если эбулиоскопическая константа воды равна 0,513.

121. В 1 кг воды растворено 0,0684 кг сахара (М = 342 г / моль). Чему равно давление насыщенного пара над этом раствором при Т = 293 К, если давление насыщенного пара над чистой водой при 293 К равна 2338,5 Па? Чему равна температура кипения раствора, если для воды  Н _исп. = 2256,7 ^. 10 ³ Дж/кг при температуре кипения?

122. Чистый кадмий затвердевает при Т = 594 К, 10%-ый раствор висмута в кадмии – при Т = 583 К. Определить энтальпию плавления кадмия.

123. Температура кристаллизации разбавленного раствора тростникового сахара

272,171 К. Давление насыщенного пара над чистой водой при этой температуре 568,6 Па, а скрытая теплота плавления льда 602,9 ^. 10 ⁴ Дж/кмоль. Вычислить давление пара над раствором.

124. 68,4 г сахарозы (М = 342 г / моль) растворено в 1000 г воды. Рассчитайте: а) давление пара; б) температуру кристаллизации; в) температуру кипения; г) осмотическое давление раствора. Давление пара чистой воды при 20 ⁰ С равно 2338,5 Па. Криоскопическая и эбулиоскопическая постоянные воды равны 1,86 и 0,52 К ^. кг / моль соответственно.

125. Некоторое количество вещества, растворенное в 100 г бензола, понижает температуру его кристаллизации на 1,28 ⁰. То же количество вещества, растворенное в 100 г воды, понижает температуру его кристаллизации на 1,395 ⁰ . Вещество находится в бензоле в молекулярной форме, а в воде полностью диссоциировано. Определить, на сколько ионов вещество диссоциирует в водном растворе. Криоскопические постоянные для бензола и воды равны 5,12 и 1,86 К ^. кг / моль соответственно.

126. Используя справочные данные по давлению насыщенного пара воды при 25 ⁰ С и значению давления паров водного раствора глицерина, равному при этой температуре 3157,06 Па, вычислить осмотическое давление этого раствора при 37 ⁰ С. Плотность раствора равна 1,0017 г / см ³ . Молярная масса глицерина равна 92,09 г / моль.

127. Компоненты А и В образуют идеальный раствор. Давление пара чистого А при 25 ⁰ С равно 100 Торр. Давление пара чистого В при данной температуре практически равно нулю. Давление пара раствора, содержащего 10г А и 1г В при 25 ⁰ С равно 95 Торр. Найти отношение молярных масс А и В.
5. Растворы сильных электролитов

Для реальных растворов вместо концентрации в термодинамические уравнения вводится активность:

a =  ^. m ,

где  - коэффициент активности растворенного электролита, m - моляльная концентрация электролита. Если электролит распадается на два иона, то стандартное состояние выбирается таким образом, чтобы выполнялось равенство:

,

где a ₊ и a _- - активности катиона и аниона соответственно. В бесконечно разбавленном растворе: a ₊ = m ; a _- = m ; a = m ² .

Коэффициент активности электролита g определяется уравнением:

g= g₊ ^. g_-,

где g₊ и g_- - коэффициенты активности катиона и аниона соответственно. Так как экспериментально определить активности катиона и аниона невозможно, вводят понятие средней ионной активности a_. Для электролита, распадающегося на два иона, a_ равна:

a _± = (a ₊ ^. a _- ) ^1/2 ,

а средний ионный коэффициент активности равен:

g_= (g₊ ^. g_-) ^1/2.

Если молекула электролита в растворе диссоциирует на  ₊ катионов и  _- анионов, то средняя ионная активность электролита равна

,

где a ₊ и a _- - активности катионов и анионов соответственно,  =  ₊ +  _- - общее число ионов, образующихся при диссоциации молекулы электролита. Средний ионный коэффициент активности электролита равен

,

где  ₊ и  _- - коэффициенты активности катионов и анионов соответственно.

В термодинамике растворов электролитов обычно используется моляльная шкала концентраций. Если концентрация раствора выражена через моляльность m, то средняя ионная активность электролита равна

,

где m _ - средняя ионная моляльность электролита:

.

Моляльность ионов (m ₊ и m_- ) в растворе связана с моляльностью раствора электролита:

.

Тогда

,

где

.

Активность электролита определяется как

.

Согласно представлениям об ионной силе раствора, коэффициенты активности ионов не зависят от природы ионов, находящихся в растворе, а зависят от ионной силы раствора (I):

,

где Z_i - зарядовое число иона, m_i - моляльная концентрация иона. Согласно первому приближению теории Дебая – Хюккеля, можно рассчитать средний ионный коэффициент активности :

,

где Z ₊ , Z _- - зарядовые числа ионов, I – ионная сила раствора, A – константа, зависящая от диэлектрической проницаемости раствора и от температуры. Для разбавленных водных растворов при T = 298 K А = 0,509. Для 1, 1 – зарядного электролита данное уравнение имеет вид:

_.

Если ионная сила раствора не превышает 0,1, коэффициенты средней ионной активности ионов равного заряда примерно одинаковы.

Пример 13. В водном растворе содержится 0,5 моль MgSO₄, 0,1 моль АlCl₃ и 0,2 моль (NH₄)₂SO₄ на 1000 г воды. Определить ионную силу раствора.

Решение. Найдем моляльность (m) всех ионов: m _Mg²⁺= 0,5 ; m _Al³⁺ = 0,1; m _(NH4)⁺ = 0,4.

Так как из 1 моль (NH₄)₂SO₄ получается 2 моль иона NH₄⁺ , m _SO4^2- = 0,5 + 0,2 = 0,7 ;

m_Cl^- = 0,3 , так как из одного моль АlCl₃ получается 3 моль – иона Cl ^- .

I = 0,5 ∑ m _ί Ζ _ί ²

Умножив моляльность каждого иона на квадрат его зарядового числаи суммируя произведения, получаем : I = 0.5 ( 0,5 ^. 4 + 0,1 ^. 9 + 0,4 ^. 1 + 0,7 ^. 4 + 0,3 ^. 1) = 3,2 .

Пример 14. Вычислить средние ионные коэффициенты активности (γ_±) для растворов

NaCl с моляльной концентрацией m₁ = 0.01 и m₂ =0,001.

Решение. Для 1-1-валентного электролита используем уравнение: lgγ_± = - 0,509m

lg γ_{± 1} = - 0,5090,01= - 0,0509; γ_±1 = 0,888 ;

lg γ_{± 2} = - 0,5090,001 = -0,016 ; γ_{± 2} = 0,963 .

Пример 15. Для раствора Cr₂(SO₄)₃ с моляльной концентрацией 0,1 вычислить среднюю ионную активность ( a_±), активность электролита, а также активности ионов Cr³⁺ и

SO₄ ^{2 -} при Т = 298К.

Решение. Рассчитаем среднюю ионную моляльность по формуле:

m _± = m ( ν₊ ^{ν+ .} ν_-^ν- )^{1/ ν} ,

где ν₊ и ν_- - число катионов и число анионов, ν = (ν₊ + ν_-) – общее число ионов

m _± = ( 2² · 3³ )^1/5 · 0,1 = 0,255 .

Вычислим среднюю ионную активность по уравнению: a_± = m _±· γ _± .

Величину γ _± берем из таблицы [1, c. 131] : γ_± = 0,0458 . Тогда

a _± = 0,255· 0,0458 = 0,0177 .

Активность электролита (a) рассчитываем по уравнению: a = (a _± ) ^ν = a ₊^ν+ ·a _-^ν- .

Чтобы найти активности ионов, сначала рассчитываем моляльности ионов:

m₊ = m · ν₊ ; m _- = m · ν _- ; m _Cr³⁺= 0,1· 3 = 0,3 ; m _SO4^2-= 0,1· 2 = 0,2 ;

Активности ионов определяем по формулам: a ₊ = γ₊· m ₊ ; a _- = γ_- · m _- ;

a _Cr³⁺ = 0,3 · 0,0458 = 0,0137 ; a _SO4^2- = 0,2 · 0.0458 = 0,0092 ;
Задачи

В задачах 128 - 162 выполнить следующие задания:

1. Определить ионную силу водного раствора электролита А с моляльной концентрацией m.

2. Определить ионную силу водного раствора электролита А с моляльной концентрацией m, если в растворе присутствует электролит В с концентрацией m₁.

3. Вычислить средний ионный коэффициент активности g_± при 298 К электролита А с концентрацией m.

4. Вычислить средний ионный коэффициент активности раствора электролита А с концентрацией m при 298 К, если в растворе присутствует электролит В с концентрацией m₁.

5. Определить среднюю ионную активность а _ раствора электролита А с концентрацией m при 298 К.

№ задачи	Электролит А	m, моль/кг Н2О	Электролит В	m1, моль/кг Н2О
128	NaCl	0,01	Ca(NO3)2	0,025
129	CdSO4	0,003	CuCl2	0,01
130	MgCl2	0,02	ZnSO4	0,015
131	Na2SO4	0,01	FeCl2	0,05
132	HNO3	0,05	H2SO4	0,02
133	KOH	0,02	Ba(NO3)2	0,04
134	HCl	0,01	CdCl2	0,02
135	CuCl2	0,005	LaBr3	0,005
136	H2SO4	0,015	KCl	0,01
137	KBr	0,02	GaCl3	0,003
138	ZnSO4	0,01	NaNO3	0,02
139	KNO3	0,05	LaCl3	0,025
140	CdCl2	0,01	HCl	0,025
141	AgNO3	0,003	Co(NO3)2	0,01
142	CsCl	0,02	H2SO4	0,015
143	HBr	0,01	Mg(ClO4)2	0,05
144	ZnBr2	0,05	HClO4	0,02
145	Co(NO3)2	0,02	ZnSO4	0,04
146	KCl	0,01	LaCl3	0,02
147	LiCl	0,005	Na2SO4	0,005
148	Na2S2O3	0,015	NaBr	0,01
149	CoCl2	0,02	NaNO3	0,003
150	NaClO3	0,01	ZnCl2	0,02
151	Mg(ClO4)2	0,05	NaCl	0,025
152	Ca(NO3)2	0,01	HNO3	0,025
153	HCl	0,01	KCl	0,05
154	H2SO4	0,01	K2SO4	0,05
155	CaCl2	0,1	KCl	0,05
156	NaH2PO4	0,02	NaCl	0,04
157	CuCl2	0,02	CuSO4	0,04
158	MgSO4	0,005	Mg(NO3)2	0,05
159	ZnSO4	0,05	CuSO4	0,07
160	KClO3	0,05	KCl	0,03
161	(NH4)2SO4	0,05	NH4NO3	0,10
162	Al2(SO4)3	0,02	AlCl3	0,03

6. Химическая кинетика сложных реакций
При кинетическом изучении сложных реакций применяют принцип независимости (являющийся одним из постулатов химической кинетики):

если в системе протекают несколько реакций, то каждая из них подчиняется основному закону химической кинетики и протекает независимо от других химических реакций.

Константа скорости элементарной химической стадии не зависит от протекания в реакционной системе других элементарных стадий. Из этого постулата следует, что скорость реакции по одному из веществ ее участников - равна алгебраической сумме скоростей тех элементарных стадий, в которых это вещество принимает участие.