ДЗФКХ07. Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
2. Фазовое равновесие в однокомпонентных системахОбщее условие равновесия фаз в однокомпонентной системе выражается уравнением Клаузиуса – Клапейрона 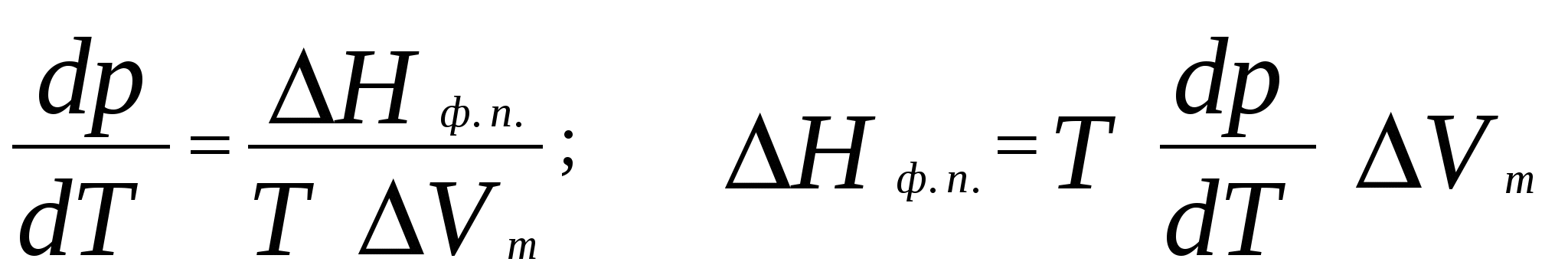 , (17) , (17)где Н ф. п. – энтальпия фазового перехода первого рода в условиях равновесия фаз (испарение, плавление, возгонка, превращение модификаций); dP/dT – температурный коэффициент давления насыщенного пара; Vm – разность молярных объемов фаз, находящихся в равновесии. Для равновесий: твердое вещество пар и жидкость пар в области температур, далеких от критической, при условии, что 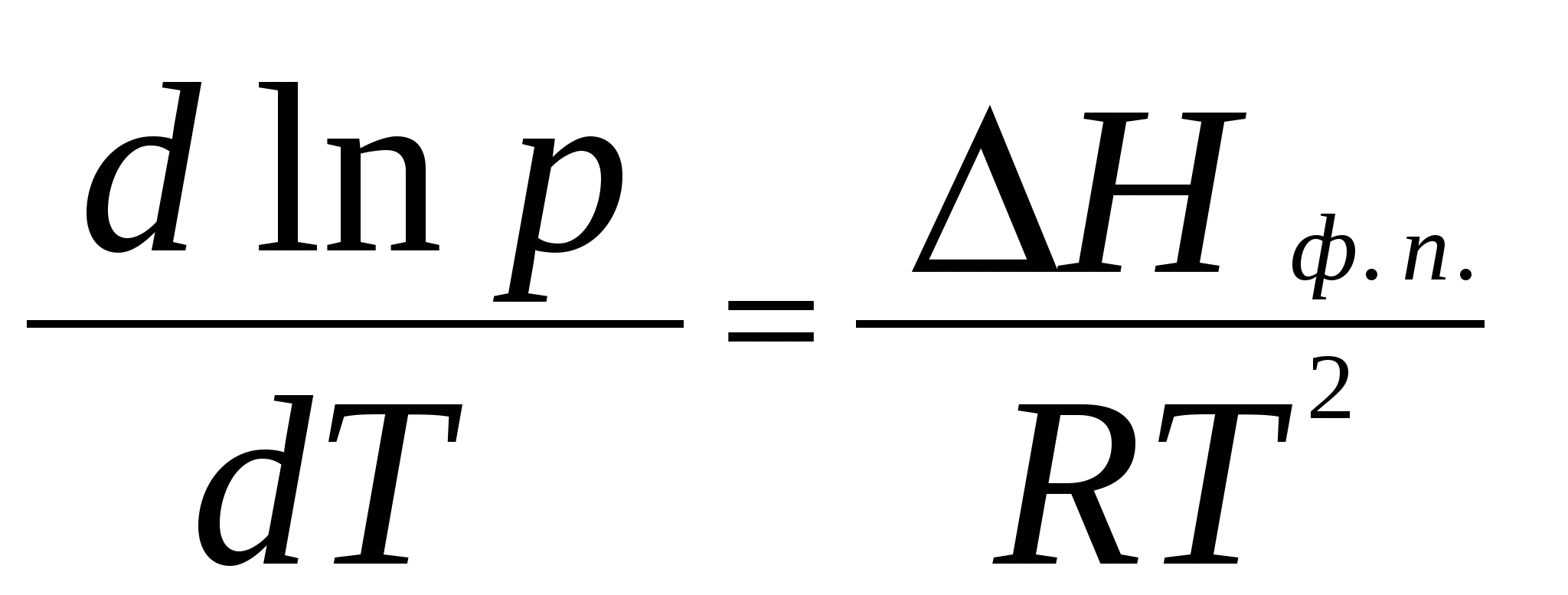 (18) (18)И нтегрирование уравнения (18) при условии, что Н ф. п .= const, приводит к уравнению 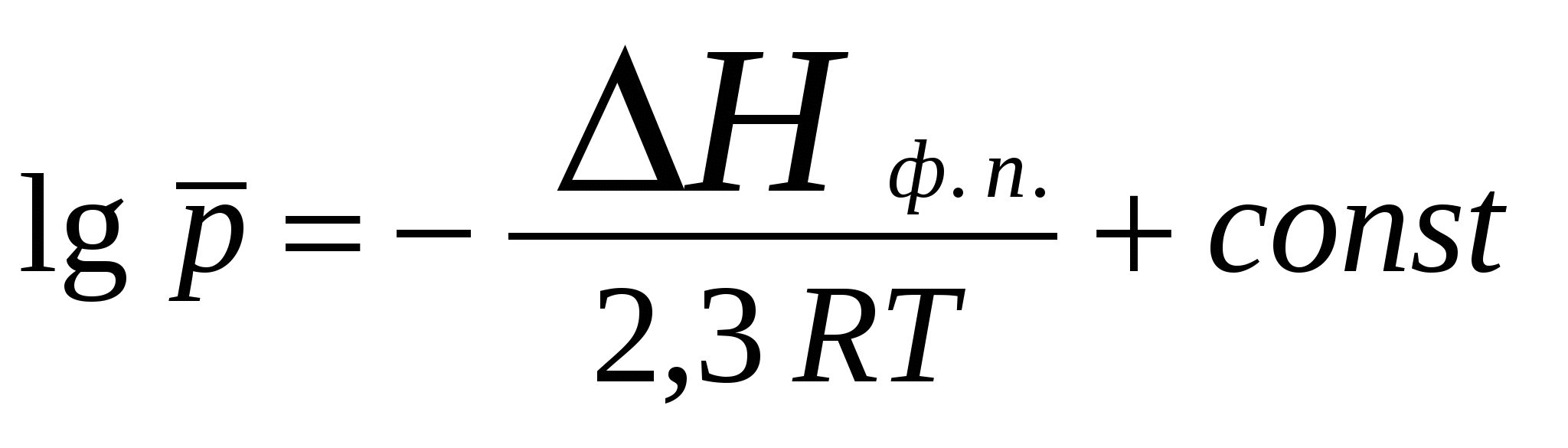 , , или 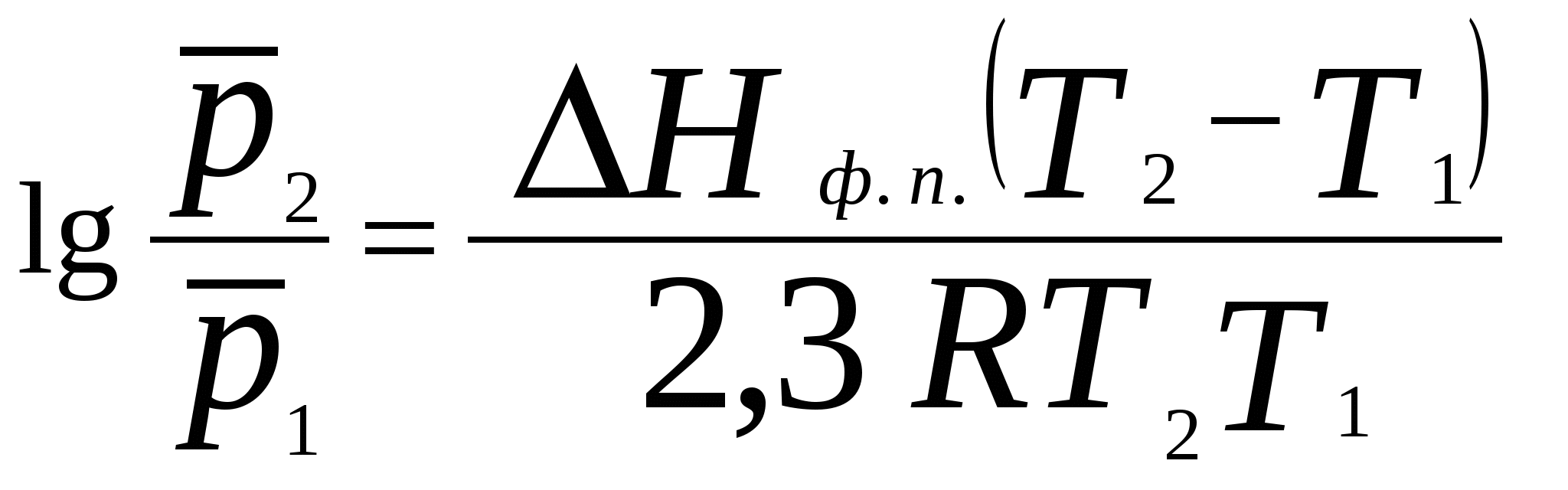 (20) (20)Значения Н ф. п. в уравнениях (19) и (20) являются средней величиной, справедливой для интервала температур Т1 - Т2. Молярные энтальпии возгонки, плавления и испарения при данной температуре связаны уравнением: Энтальпию испарения жидкости можно приближенно оценить по правилу Трутона, согласно которому молярная энтропия испарения в нормальной точке кипения (при p = 1 атм) приблизительно постоянна: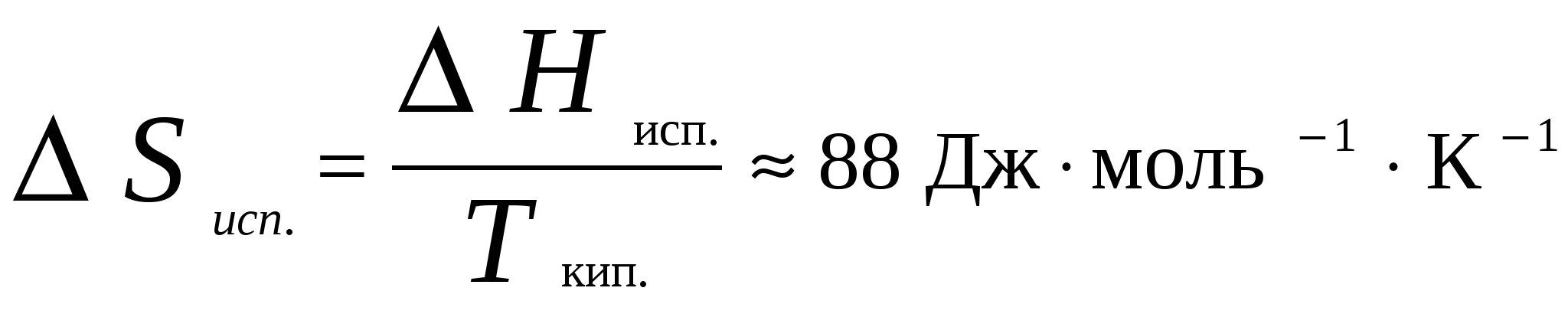 . .Зависимость теплоты фазового перехода от температуры описывается уравнением:где C и C - теплоемкости находящихся в равновесии фаз и . В небольшом интервале температур С ф. п .= const, тогда или С учетом уравнения (21) уравнение (17) в интегральной форме принимает вид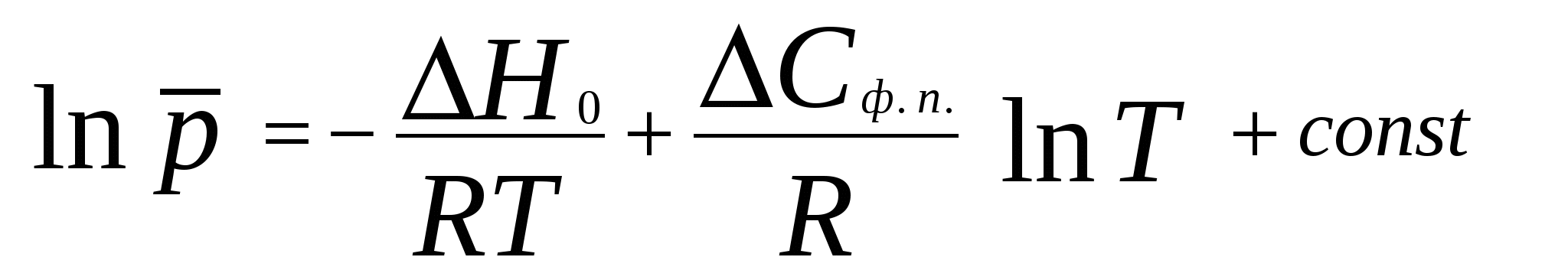 . .Пример 5. Зависимость давления насыщенного пара от температуры для HCN выражается уравнением: lg p = 9,16 – 1237 / Т . Определить теплоту испарения при температуре кипения. Решение. При p = 1,013 · 105 Па ; Т = Тн.т.кип. и, следовательно, lg 1,013 · 10 5 = 9,16 – 1237 / Т н.т.кип ; Откуда, Т н.т.кип = 299 К . Для расчета ΔН исп. воспользуемся уравнением Клаузиуса Клапейрона: 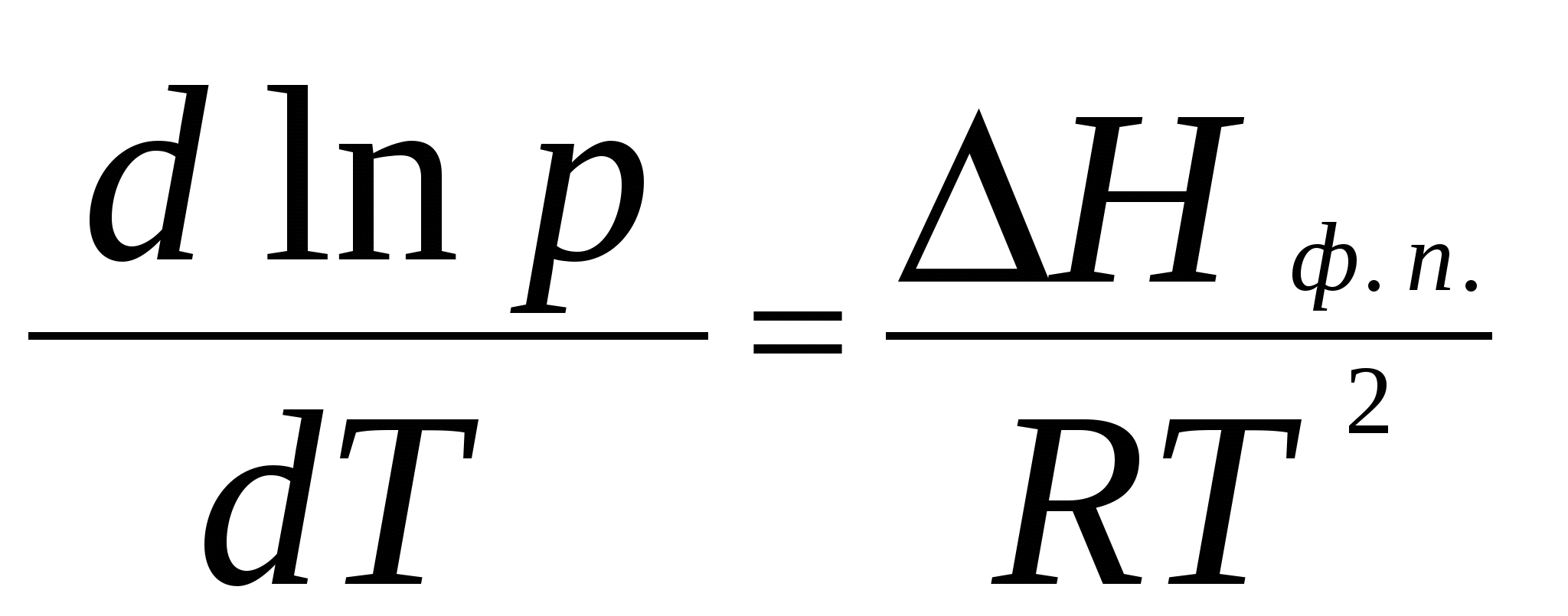 . .Найдем dlnp / dT , дифференцируя уравнение зависимости давления пара от температуры: d ln p / dT = 2,3 · 1237 / Т2 . Вычислим ΔНисп. при Тн.т.кип = 299 К : ΔНисп. = RT 2 · d ln p / dT = R · 2,3· 1237 ΔН исп. = 8,314 · 2,3· 1237 = 23654 Дж/ моль. Пример 6. Температура кипения бензола при давлении p = 1,013 · 105 Па равна 353,3 К. Определить давление пара бензола при 298,2 К. Решение. Давление пара бензола при Т1 = 353,3 К равно p 1 = 1,013 · 105 Па. По правилу Трутона : ΔSисп. = ΔНисп./ Ткип.= 88 Дж / моль·К. Отсюда определим ΔНисп. : ΔНисп. = 88 · 353,3 . 10 - 3 = 31,1 кДж / моль . Подставим эти данные в интегральную форму уравнения Клаузиуса –Клапейрона : ln (p 2 / p 1) = ΔНисп. / R ( 1/ Т1 – 1 / T2 ) ln (p 2 / 1,013 · 10 5) = (31100 / 8,314) ( 1/ 353,3 – 1 / 298,2 ) Откуда p 2 = 1,428 · 10 4 Па. Пример 7. Зависимость давления насыщенного пара (в Торр) от температуры для твердого и жидкого SO2 выражается уравнениями: lg p(тв.) = 10,5916 – 1871,2 / Т; lg p (ж.) = 8,3186 – 1427,7 / Т. Рассчитать температуру и давление в тройной точке. ( 1 Торр = 1мм.рт. ст. = 133,32 Па ) Решение. Так как для равновесных фаз в тройной точке справедливо условие: p 0ж = p 0тв , приравняв приведенные уравнения, вычислим температуру и давление в тройной точке: 10,5916 – 1871,2 / Т = 8,3186 – 1427,7 / Т . Откуда Ттр.т. = 195,1 К. lg pтр.т. = 8,3186 – 1427,7 / 195,1 = 1,0008 ; pтр.т. = 0,046 Па . Задачи В задачах 46 - 50 рассчитать теплоту испарения при температуре кипения, а также давление насыщенного пара при T = 298 К, если известна зависимость давления насыщенного пара от температуры.
51. Определить температуру кипения хлорбензола C6H5Cl при p = 266,6 Па, если его нормальная температура кипения 405,4 К, а при p= 5,332 . 10 4 Па он кипит при 382,2 К. Вычислить теплоту испарения Н исп.. 52. Энтальпия плавления и плотность жидкой и твердой ртути при температуре тройной точки (234,29 К) равны соответственно 11,8 . 10 3 Дж / кг; 13,690 кг/м3; 14193 кг/м3. Вычислить изменение давления, необходимое для изменения температуры плавления ртути на 1 К. 53. Вычислить температуру плавления, давление насыщенного пара при температуре плавления, а также и теплоту плавления серебра ( Н пл )по данным зависимости давления насыщенного пара (Па) от температуры, если: 1. для твердого серебра lg p = 13,892 - 1,402 . 10 4 / T; 2. для жидкого серебра lg p = 13,347 - 1,334 . 10 4/ T. 54. Рассчитать теплоту возгонки металлического цинка, если теплота плавления Н пл. при температуре тройной точки (692,7 К) равна 6,908 к Дж /моль, а зависимость теплоты испарения от температуры описывается уравнением: Н исп = 133738,66 - 9,972 Т (Дж/моль) 55. Зависимость давления насыщенного пара этилового эфира (C2H5)2O от температуры представлена данными:
Построить график зависимости lg p от 1/Т и определить молярную теплоту испарения эфира (по тангенсу угла наклона прямой), а также нормальную температуру кипения. 56. Давления паров воды при 95 и 97 0С соответственно равны 84513 и 90920 Па. Вычислить теплоту испарения воды (Дж / моль) и количество теплоты, необходимое для испарения 100 кг воды. 57. Давление паров иода при 90 0С равно 3572,4 Па, а при 100 0С – 6065,15 Па. Определить давление паров иода при 115 0С. 58. Давление паров жидкого аммиака при (- 10 0С) равно 2,907.10 5 Па, а при 0 0С – 4,293 . 10 5 Па. Определить давление паров жидкого аммиака при температуре (- 5 0С). 59. Давление насыщенных паров ртути при 90 0С равно 20,91 Па, а при 100 0С – 36,16 Па. Определить теплоту испарения 10 кг ртути в указанном интервале температур и давление насыщенных паров ртути при 106 0С. 60. Вычислить давление насыщенных паров сероуглерода при (- 10 0С), если давление пара при 0 0С равно 16929 Па. Удельная теплота испарения сероуглерода равна 363,3 Дж/г. 61. Температура плавления свинца равна 327,4 0 С, разность молярных объемов свинца в жидком и твердом состояниях 0,66 см 3 / моль, удельная теплота плавления свинца 23,04 Дж /г. Определить изменение температуры плавления при повышении давления по сравнению с нормальным в 10 раз. 62. Температура плавления бензола 5,49 0С. Разность молярных объемов бензола в жидком и твердом состояниях V = 10,28 см 3/моль. При какой температуре будет плавиться бензол под давлением 1,013 . 10 7 Па? Удельная теплота плавления бензола равна 125,7 Дж/г. 63. Рассчитать разность молярных объемов для воды (V = V ж – V тв.), если при повышении давления на 1 Па температура плавления льда понижается на 7,5 . 10 – 8 град (dT / dp). Удельная теплота плавления льда равна 333,7 Дж / г. 64. Температура плавления кадмия равна 322 0С, его удельная теплота плавления равна 57400 Дж / кг. Плотности твердого и жидкого кадмия соответственно равны 8366 и 7989 кг / м 3. Вычислить, на сколько повысится температура плавления кадмия при увеличении давления от 101325 Па до 10132500 Па. 3. Закон распределения. Экстракция Закон распределения выражается уравнением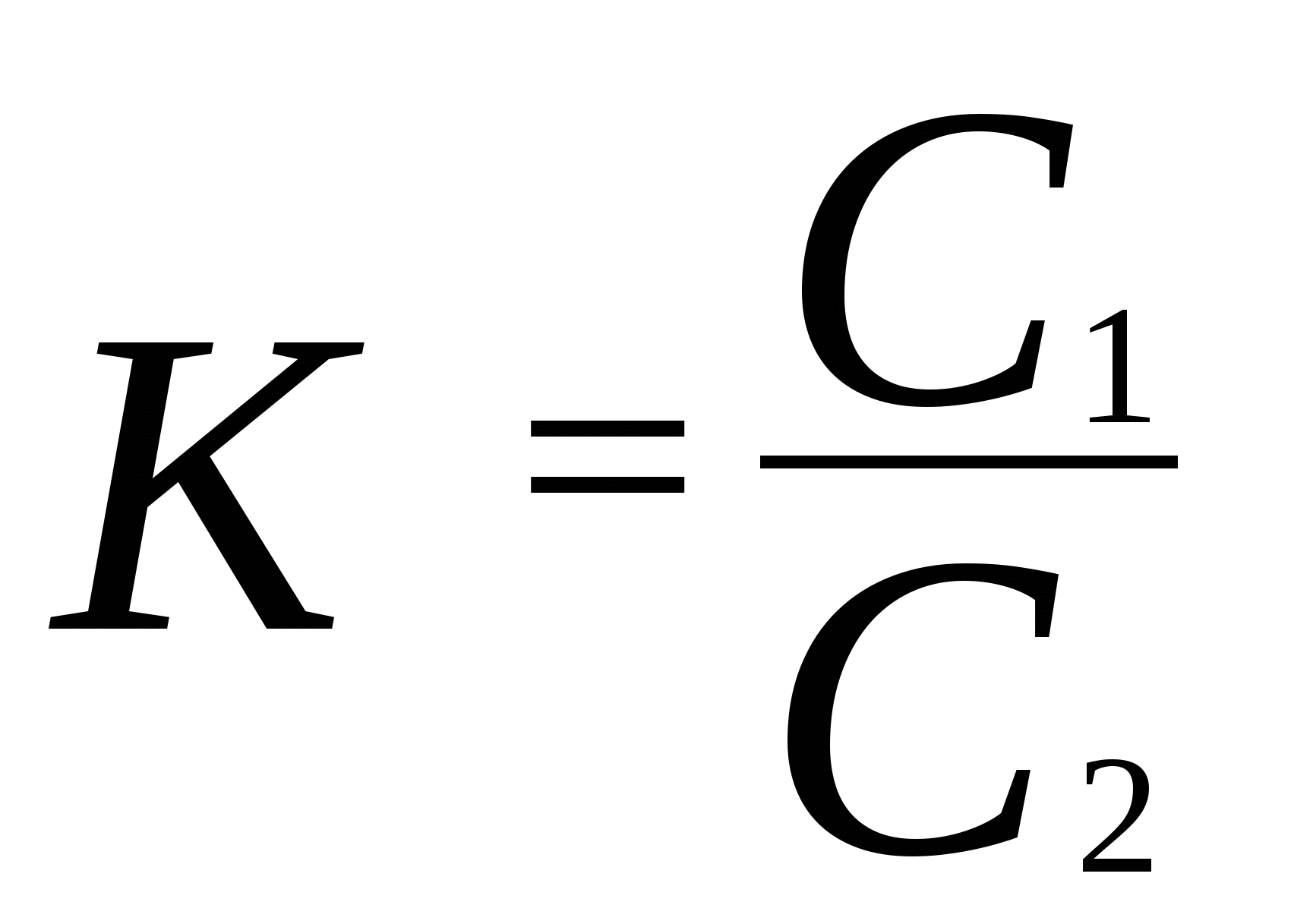 , ,где K – константа распределения; С1 и С2 – равновесные концентрации данного вещества при Т = const в 1-й и 2- й фазах. Если в фазе 2 вещество ассоциировано n A (A) n, то справедливо выражение 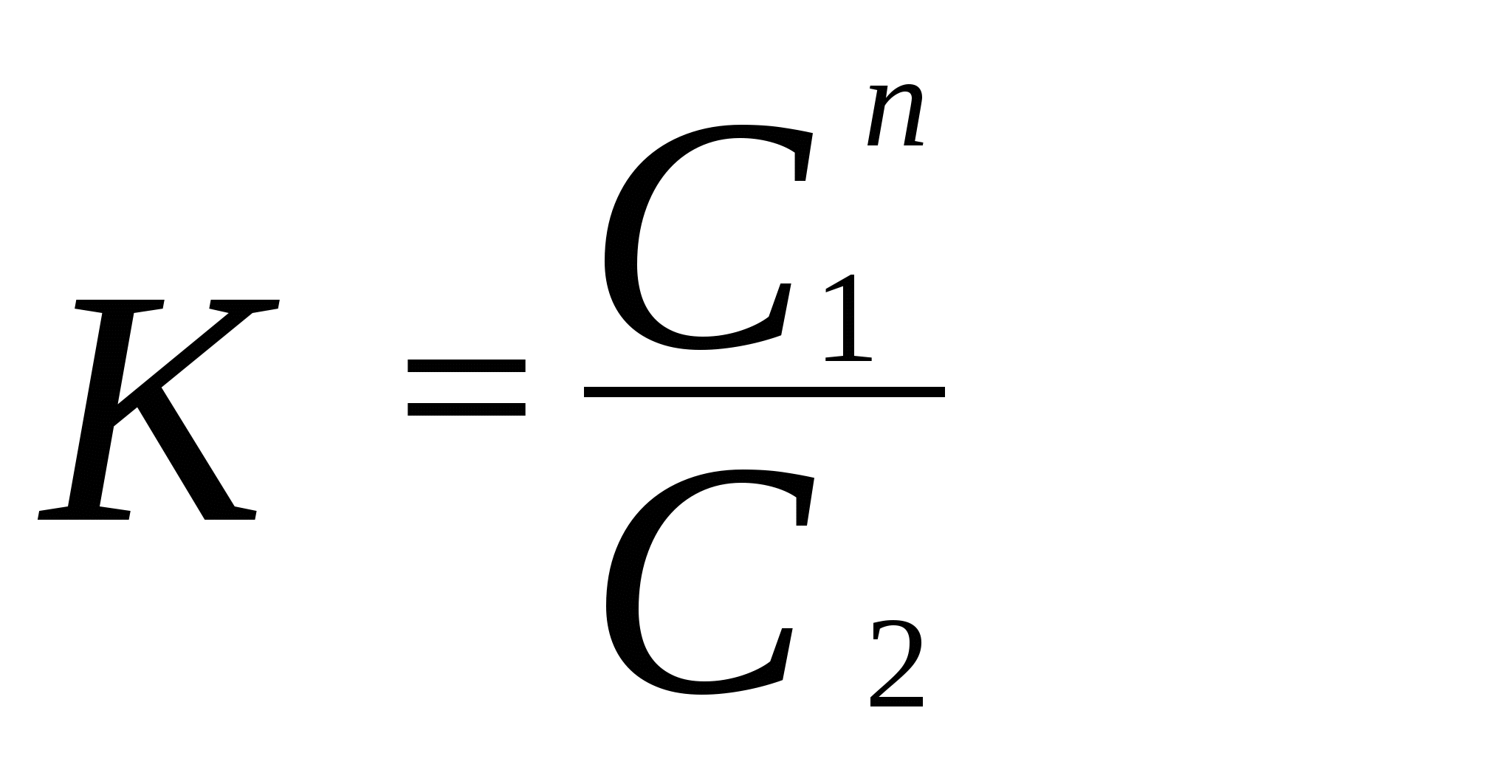 . (22) . (22)Если 1 – степень диссоциации вещества в первом растворителе, а 2 – во втором, то 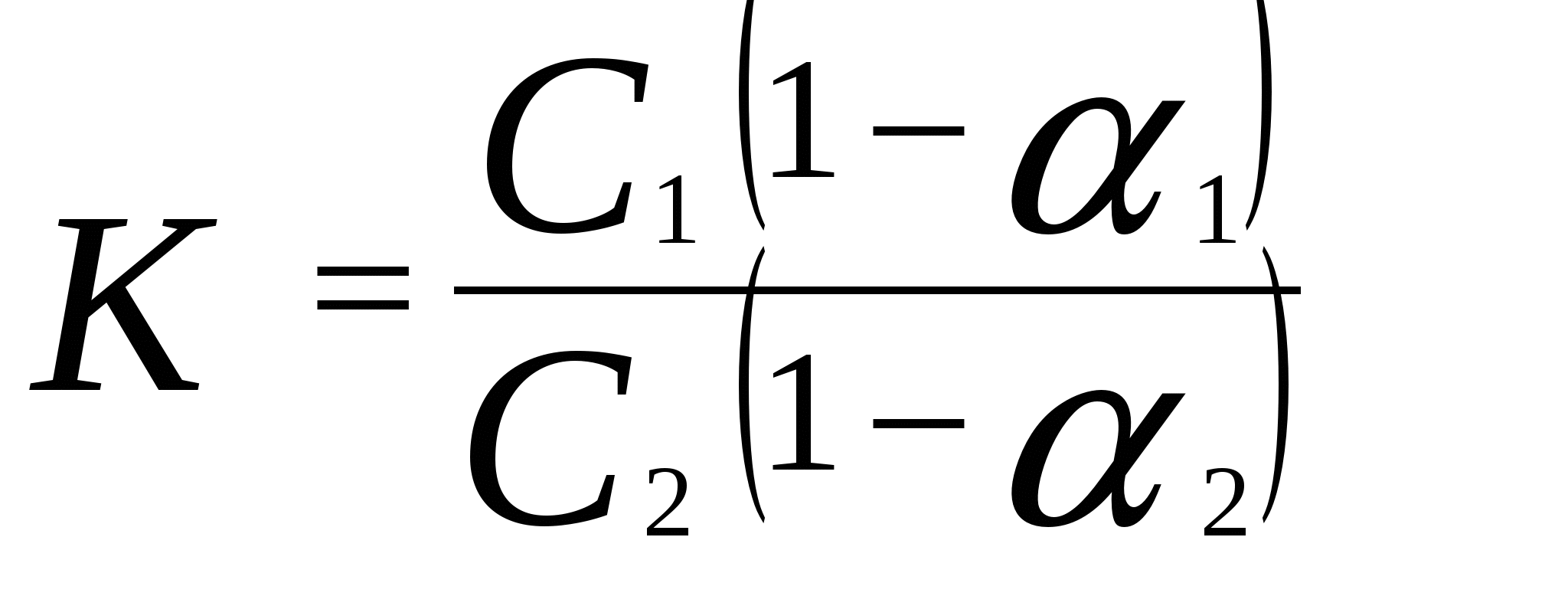 . .Закон распределения широко используется для решения задач на экстракцию. Пусть g 0 – исходное количество экстрагируемого вещества; V1 – объем раствора, в котором находится вещество; V2 – объем растворителя, потребляемого на одно экстрагирование, m – общее число экстрагирований; g 1, g 2, …, g m – количество вещества, остающееся в первоначальном растворе после 1, 2, … m - го экстрагирования; K– константа распределения, которую условились обозначать отношением концентрации раствора, из которого экстрагируется вещество, к концентрации раствора, которым производится экстрагирование. Тогда 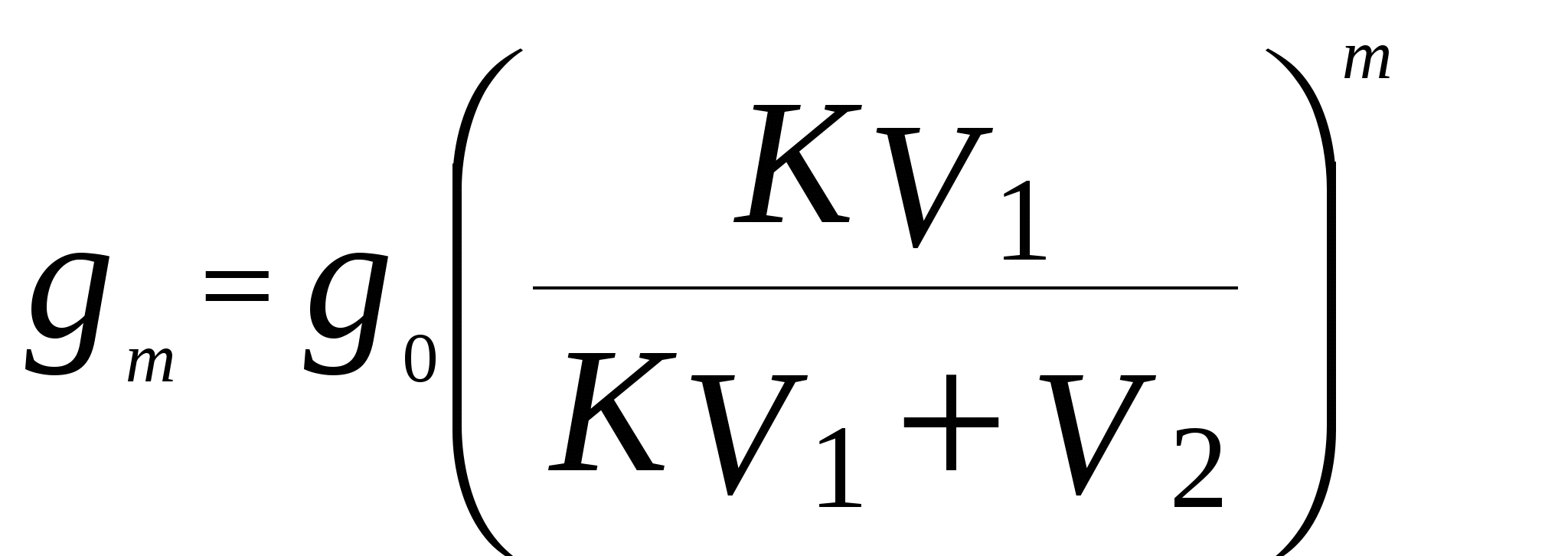 . (23) . (23)Пример 8. Коэффициент распределения иода между водой и бензолом равен 0,017. Водный раствор иода, содержащий 1кг I2 в 1м3 воды взбалтывают с бензолом. Определить, какое количество I2 останется в водном растворе: а) если 1м3 водного раствора взболтать с 0,05 м3 бензола ; б) если 1м3 водного раствора взболтать последовательно пятью отдельными порциями бензола по 0,01 м3 каждая. Решение. а) В первом случае производится всего одно экстрагирование, следовательно, по уравнению: g 1 = g 0 ( KV1 / KV1 + V2 ) вычислим количество I2 , оставшееся в водном растворе: g 1 = 1 ( 0,0017 · 1 / 0,0017 · 1 + 0,05 ) = 0,033 кг Масса экстрагированного йода равна: 1 – 0,033 = 0,967 кг . б) При пяти экстрагированиях следует применить уравнение: g m = g 0 ( KV1 / KV1 + V2 )m g 5 = 1 (0.0017 · 1 / 0,0017 · 1 + 0,01) 5 = 0,000065 кг Масса экстрагированного иода равна: ( 1 - 0,000065 ) = 0,999935 кг . Таким образом, при затрате одного и того же количества бензола в первом случае было экстрагировано 96,7 % I2 , а во втором – практически весь йод полностью. Пример 9. При изучении распределения уксусной кислоты между четыреххлористым углеродом и водой были получены следующие данные:
В CCl 4 уксусная кислота частично ассоциирована. Определить коэффициент ассоциации уксусной кислоты (n) и константу распределения K. Решение. Представим уравнение (22) в логарифмическом виде: lg K = n lg C 1 - lg C 2 , lg C 2 = n lg C 1 - lg K. Составим вспомогательную таблицу:
Необходимо построить график зависимости lg C 2 от lg C 1 . Угловой коэффициент будет равен n, а отрезок, отсекаемый на оси ординат (- lg K). Из графика получаем следующие результаты: n 2; lg K =1,95; K 89. Задачи 65. Константа распределения иода между водой и четыреххлористым углеродом CCl4 при Т = 298 К равна 0,0117. В обоих растворителях I2 имеет одинаковую молярную массу. Какой объем CCl4 следует взять, чтобы однократным экстрагированием извлечь из 0,5 . 10 3 м 3 водного раствора 99,9; 99,0; 90,0% всего растворенного в нем йода? 66. Константа распределения иода между водой и сероуглеродом CS2 равна 0,0017. Водный раствор иода, содержащий 1 кг J2 в 1 м3, взбалтывается с CS2. Какое количество I2 останется в водном растворе, если: а) 1 м3 водного раствора взболтать с 0,05 м 3 сероуглерода; б) 1 м3 водного раствора последовательно взболтать с пятью порциями CS2 по 0,01 м3 каждая? 67. Константа распределения сернистого газа SO2 между водой и хлороформом равна 0,953. Сколько воды нужно добавить к 1 м3 раствора SO2 в хлороформе, чтобы извлечь 25% SO2? 68. Константа распределения лимонной кислоты между водой и эфиром равна 155. Сколько воды нужно добавить к 0,025 м3 раствора кислоты в эфире, чтобы извлечь 25% кислоты? 69. Водный раствор пикриновой кислоты с концентрацией 0,02 кмоль/м3 находится в равновесии с раствором этой же кислоты в бензоле. Концентрация бензольного раствора 0,07 кмоль/м3. Вычислить константу распределения пикриновой кислоты между бензолом и водой, если в бензольном растворе пикриновая кислота имеет нормальную молярную массу, в воде – частично диссоциирована, причем степень диссоциации равна 0,9. 70. Какое количество иода останется в 0,001 м3 водного раствора, который был насыщен при 298 К, после взбалтывания его с 0,1 . 10 - 3 м 3 сероуглерода? Растворимость иода в воде 0,001 кг на 3,616 . 10 - 3 м 3, константа распределения иода между водой и сероуглеродом 0,0017. Молярная масса йода в обоих растворителях одинакова. 71. Константа распределения уксусной кислоты между водой и эфиром равна 1,87. Сколько эфира нужно прибавить к 0,001 м3 водного раствора, чтобы извлечь из него половину кислоты? 72. К 0,005 м3 раствора йода в эфире, содержащего 0,0173 кг иода, прибавлено 0,002 м3 раствора иода в глицерине, содержащего 0,0207 кг иода. Определить концентрацию иода в равновесных растворах, если известно, что константа распределения иода между глицерином и эфиром равна 0,2. 73. При Т = 298 К водный раствор янтарной кислоты, содержащий 12,1 кг/м3 кислоты, находится в равновесии с эфирным раствором, содержащим 2,2 кг/м3 кислоты. Какова концентрация эфирного раствора янтарной кислоты, находящегося в равновесии с водным раствором, содержащим 4,84 кг/м3 кислоты? Янтарная кислота имеет нормальную молярную массу в воде и в эфире. 74. Коэффициент распределения масляной кислоты между водой и амиловым спиртом равен 0,09. Исходная концентрация кислоты в водном растворе равна 0,05 моль/л. С каким объемом амилового спирта необходимо смешать 1 л исходного раствора, чтобы ее остаточная концентрация составила 0,012 моль / л? 75. Экстракцию иодида ртути из водного раствора проводят равными порциями бензола. Для этого смешивают 1 л водного раствора иодида ртути с 0,01 л бензола и после достижения равновесия жидкости отделяют. Сколько необходимо провести таких операций, чтобы снизить содержание иодида ртути с 0,001 моль / л до 0,00001 моль / л, если коэффициент распределения между водой и бензолом равен 0,026? 76. Распределение пероксида водорода в системе «вода – пентанол» характеризуется следующими данными:
Определить среднее значение коэффициента распределения. 77. Определить среднее значение коэффициента распределения диметиламина в системе «вода (С 1) – бензол (С 2)» по следующим данным:
78. Определить коэффициент ассоциации (n) пикриновой кислоты в системе «вода (С 1) – хлороформ (С 2)» по следующим данным:
79. Определить коэффициент ассоциации (n) муравьиной кислоты в системе «вода (С 1) – хлороформ (С 2)» по следующим данным:
80. Взбалтывают 1 л воды с 400 мл амилового спирта, содержащими 2,5 г йода. Вычислить количество йода, перешедшего в водный слой. Коэффициент распределения йода между амиловым спиртом и водой равен 230. 81. При изучении распределения салициловой кислоты между бензолом и водой при 25 0С были получены следующие данные:
Определить графически значения K и n и написать формулу закона распределения для данного случая. 82. Коэффициент распределения иода между водой и сероуглеродом 0,0017. Водный раствор объемом 100 мл, содержащий 0,2 г/л йода, взболтали с 60 мл сероуглерода. Определить степень извлечения иода (%) при однократном извлечении всей порцией сероуглерода и при трехкратном взбалтывании порциями по 20 мл сероуглерода. Йод имеет нормальную молярную массу в воде и сероуглероде. 83. Коэффициент распределения нормальной масляной кислоты С3Н7СООН между хлороформом и водой равен 0,52 при 25 0С. Какое количество масляной кислоты можно извлечь из 100 мл 0,5 М раствора масляной кислоты в хлороформе при встряхивании его однократно со 100 мл воды и при четырехкратном встряхивании, используя каждый раз по 25 мл воды? 84. В 1 л раствора хлорида ртути (II) в бензоле содержится 0,5 г HgCl 2. Сколько экстрагирований необходимо сделать водой порциями по 20 мл, чтобы остаток соли в исходном растворе составлял 1 % от первоначального количества? Коэффициент распределения хлорида ртути между бензолом и водой при 25 0С равен 0,084. 85. При действии на амиловый спирт перманганата калия образуется раствор валериановой кислоты в спирте. Какое количество кислоты можно извлечь из 100 мл полученного раствора, содержащего 3,7 г кислоты, экстракцией 30 мл диэтилового эфира? Коэффициент распределения валериановой кислоты в указанной системе равен 0,043. 86. При синтезе фенилуксусной кислоты часть продукта растворяется в воде. Какое количество кислоты можно извлечь из 100 мл водного раствора, содержащего 2,5 г кислоты, 40 мл экстрагента двукратной экстракцией, если в качестве экстрагента взяли: а) толуол (K = 0,28); б) хлороформ (K = 0,09)? Какой из названных растворителей лучший экстрагент? 87. Для повторного использования отработанных вод, содержание фенола в них необходимо снизить до 0,5 кг / м 3. Достаточна ли для этого четырехкратная обработка 10 м 3 этих вод бензолом, если каждый раз использовать по 1 м 3 свежего экстрагента? Начальное содержание фенола в отработанных водах равно 8,0 кг / м 3; коэффициент распределения фенола в системе вода – бензол равен 0,20. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
