ДЗФКХ07. Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005

• Название: Методические указания к решению задач домашнего задания по курсу Физическая и коллоидная химия Москва 2005
• Анкор: ДЗФКХ07.doc
• Дата: 25.05.2018
• Размер: 0.71 Mb.
• Имя файла: ДЗФКХ07.doc
• Тип: Методические указания; #19623
• страница: 4 из 5

Для мономолекулярных обратимых реакций типа А  В дифференциальная форма кинетического уравнения имеет вид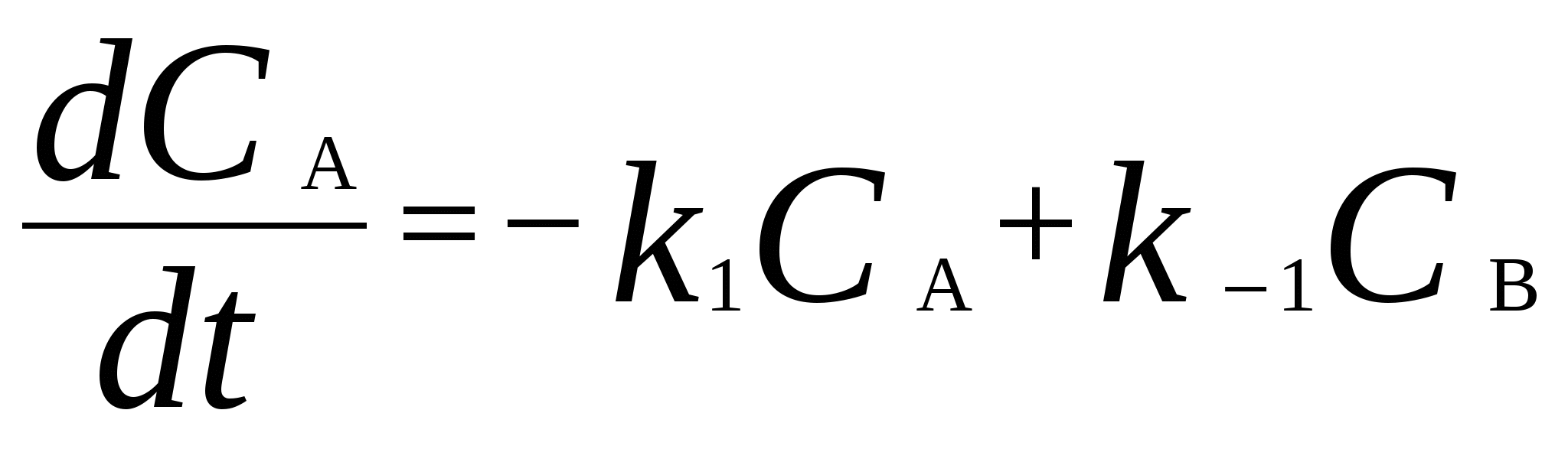

.

Здесь k ₁ – константа скорости прямой реакции, k_{– 1} – константа скорости обратной реакции. При равновесии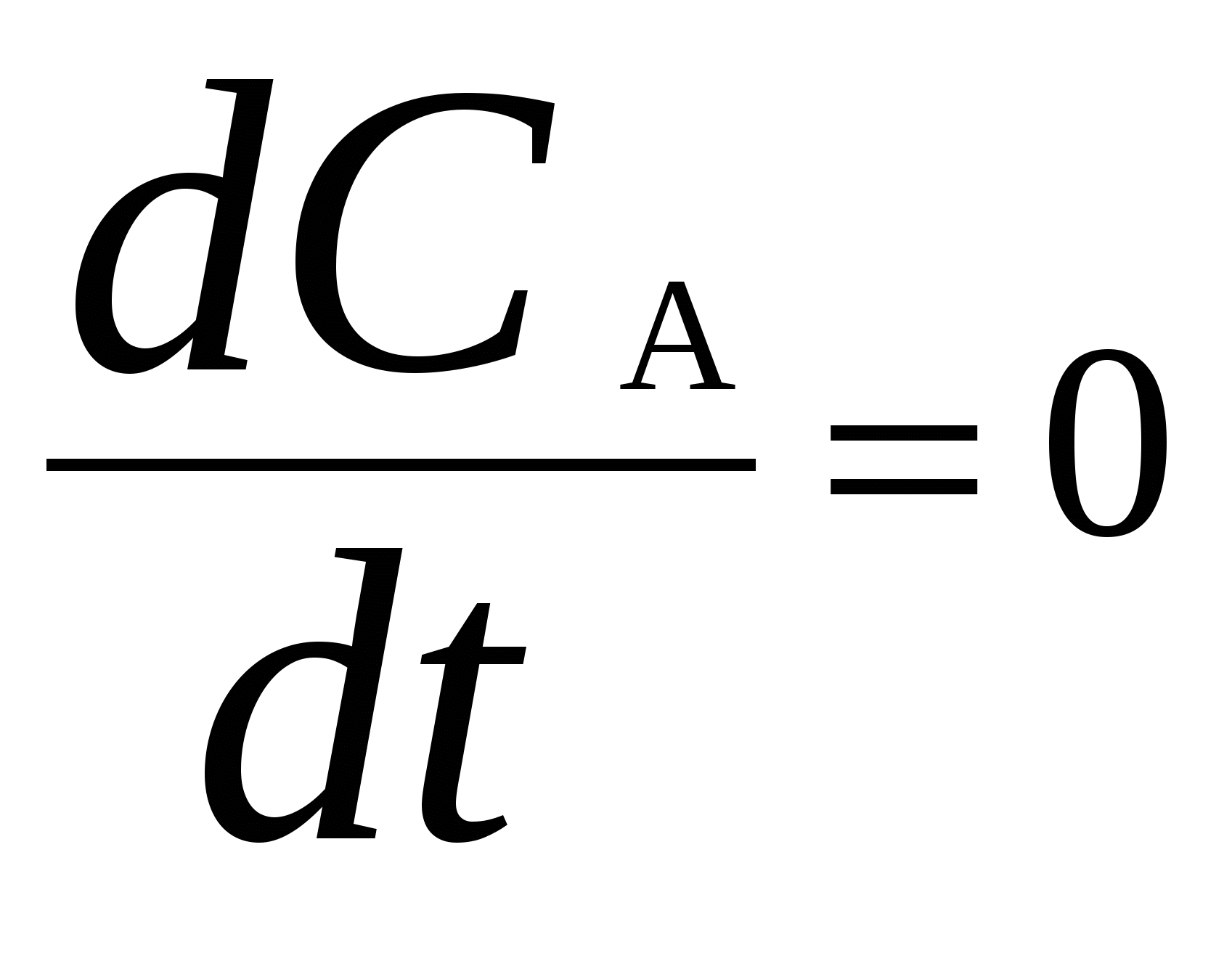

.

Если при t = 0 С _B = 0, то справедливы следующие соотношения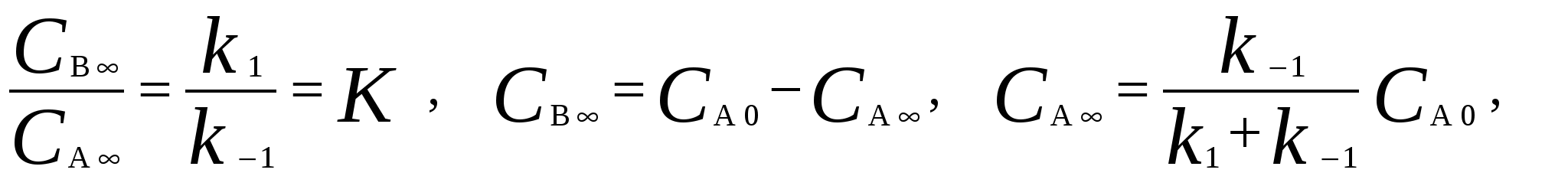



где С _А, С _B - текущие концентрации веществ A и B; С _{А 0} - начальная концентрация A при t = 0; k ₁ и k _{– 1} – константы скоростей прямой и обратной реакций; С_{А } и С _{В } - равновесные концентрации A и B; K – константа равновесия. Интегральная форма кинетического уравнения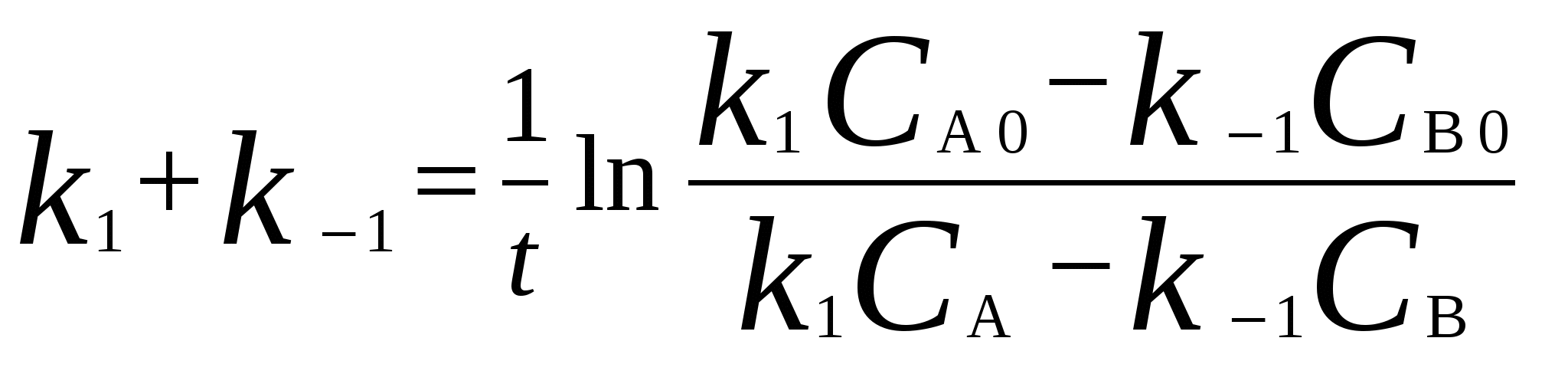

.

При условии, что при t= 0 С _{B 0} = 0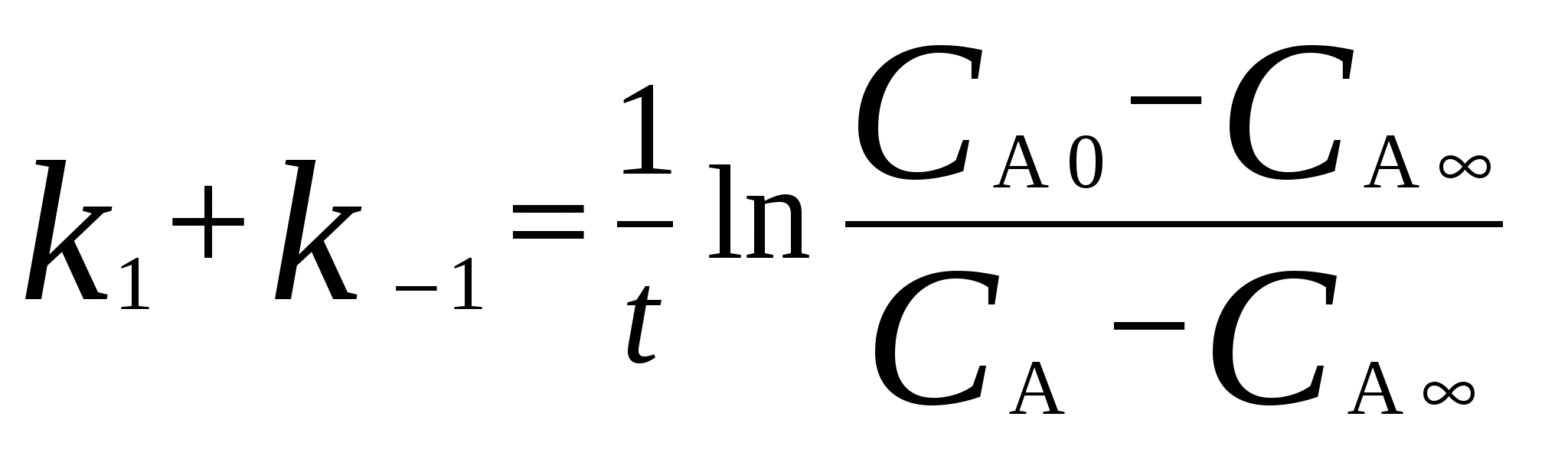

.

Для мономолекулярных параллельных реакций типа

B (k₁)

A

C (k ₂)

дифференциальная форма кинетического уравнения имеет вид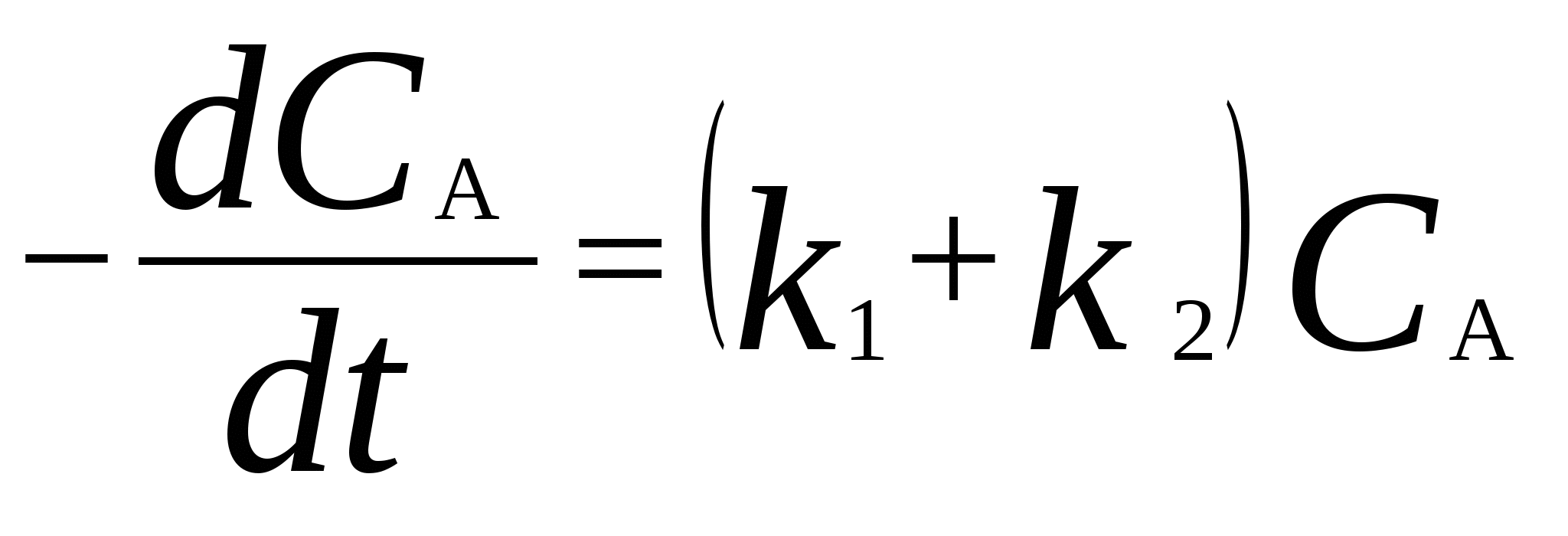

.

Интегрирование приводит к следующему результату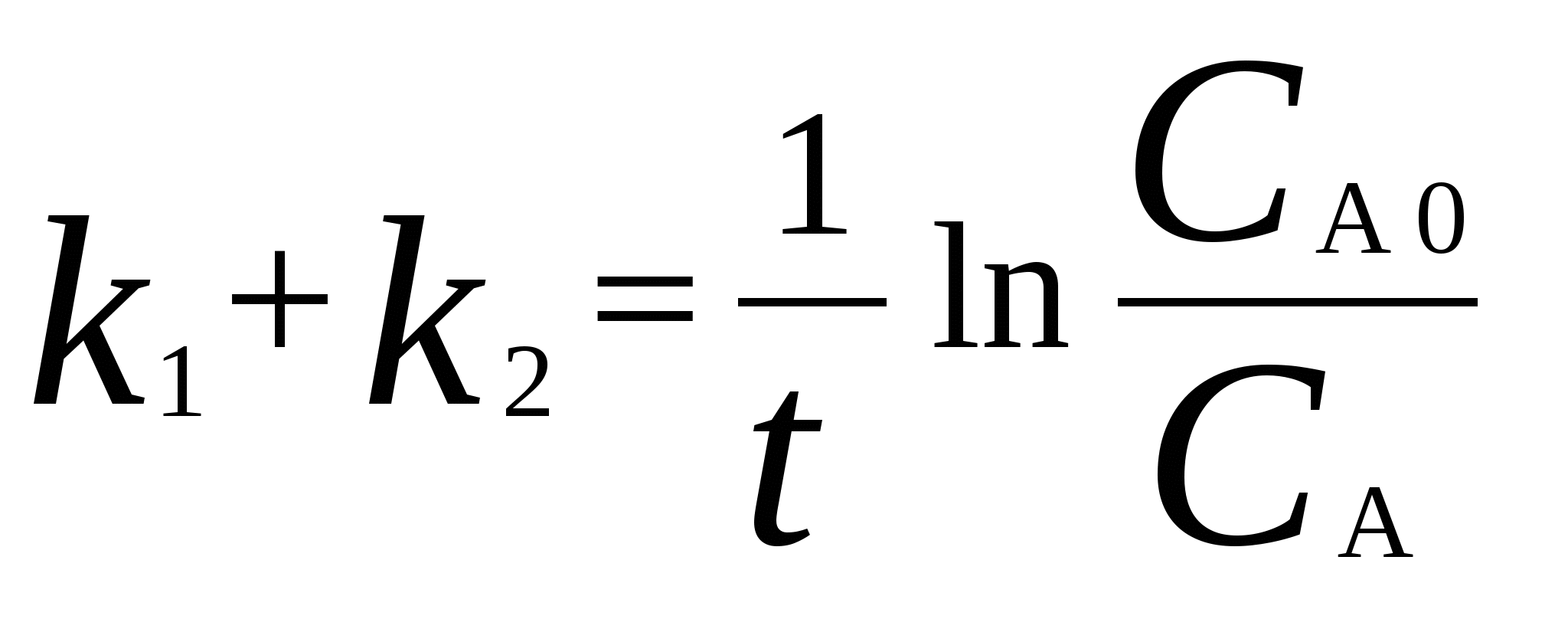

,

где k ₁ и k ₂ – константы скоростей первой и второй реакций. Константы скоростей отдельных стадий для реакций данного типа определяют по соотношению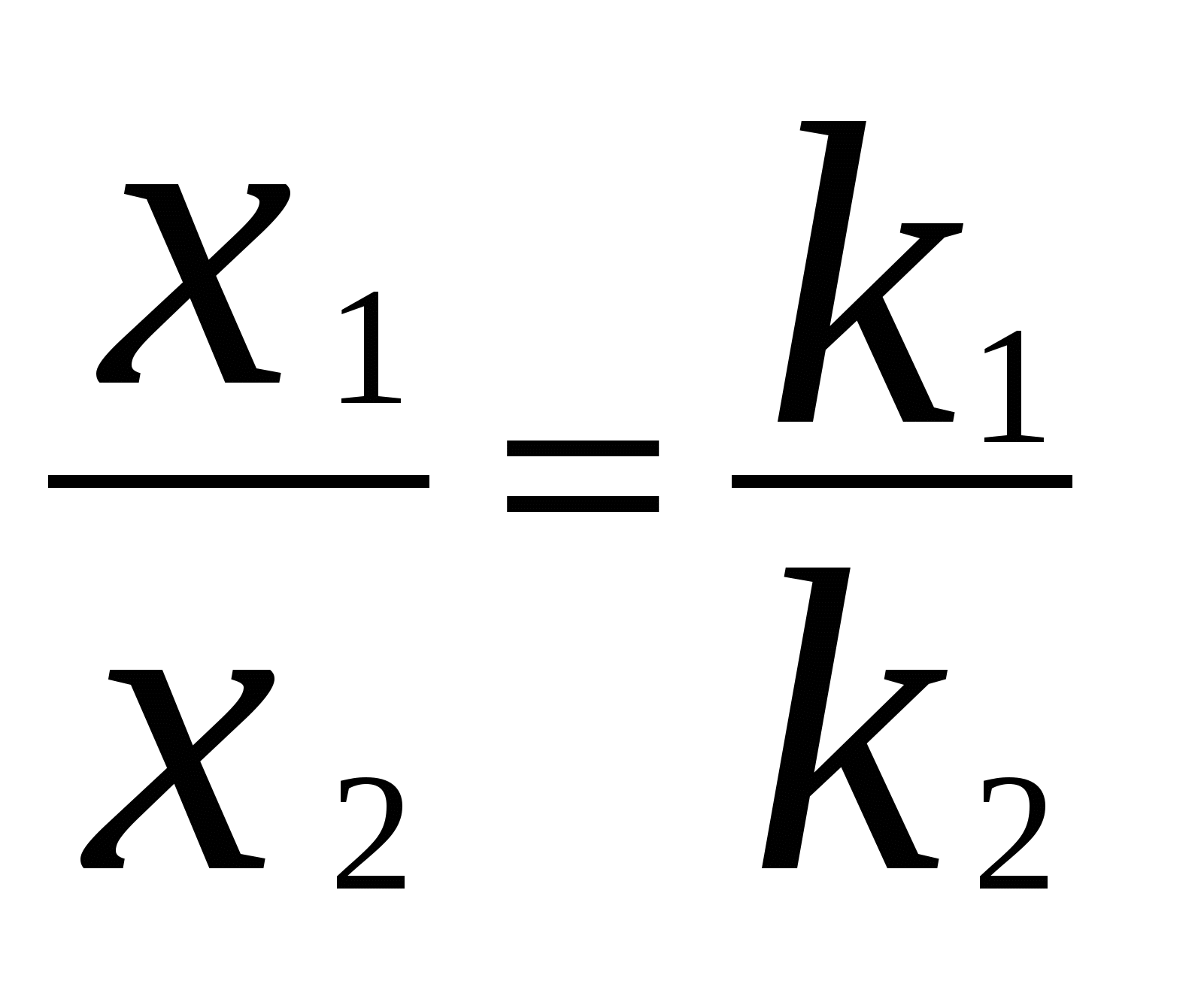

,

где x ₁ и x ₂ – количества моль веществ B и C, образовавшихся к моменту времени t.

Для последовательных реакций первого порядка типа

дифференциальные кинетические уравнения имеют вид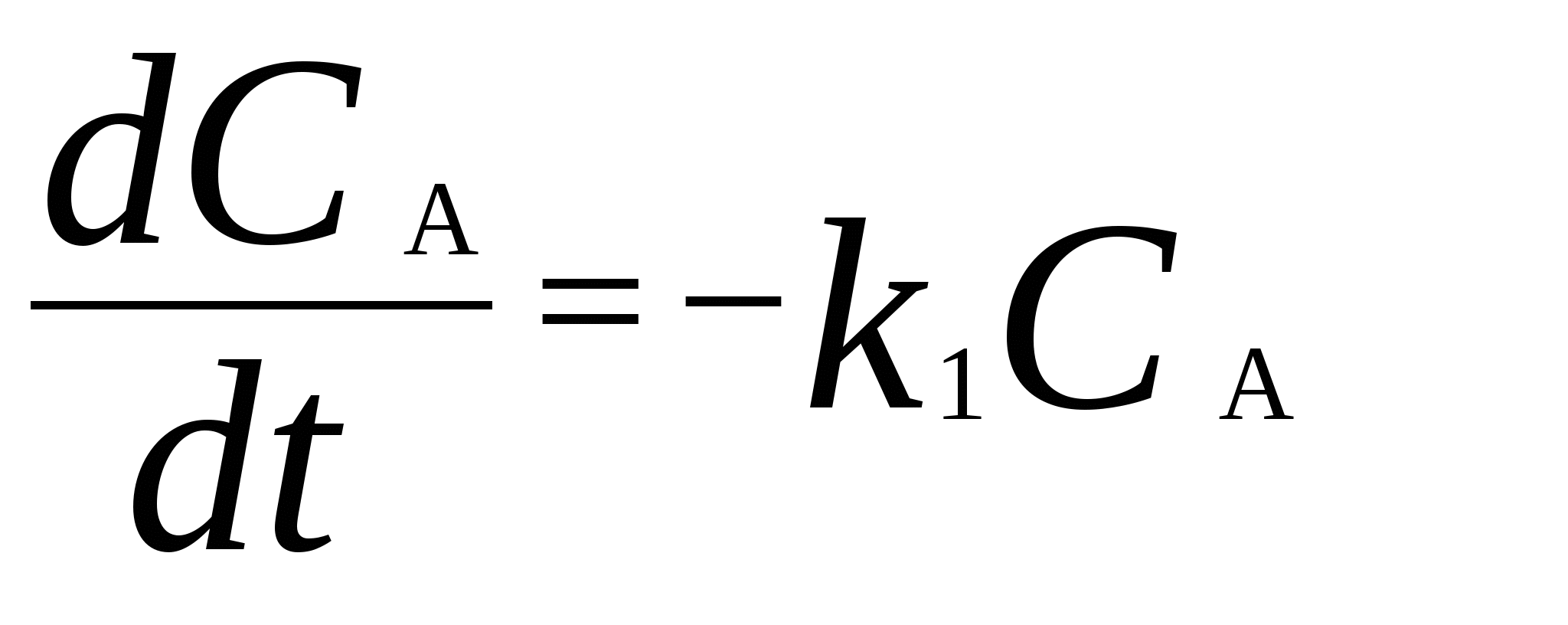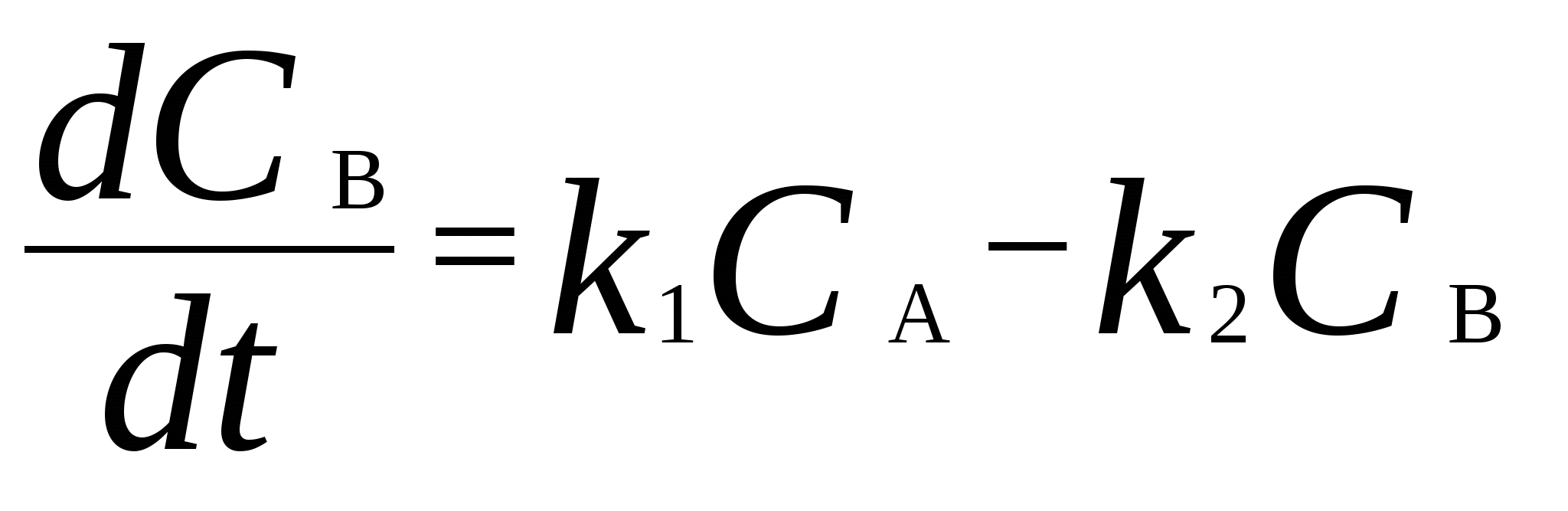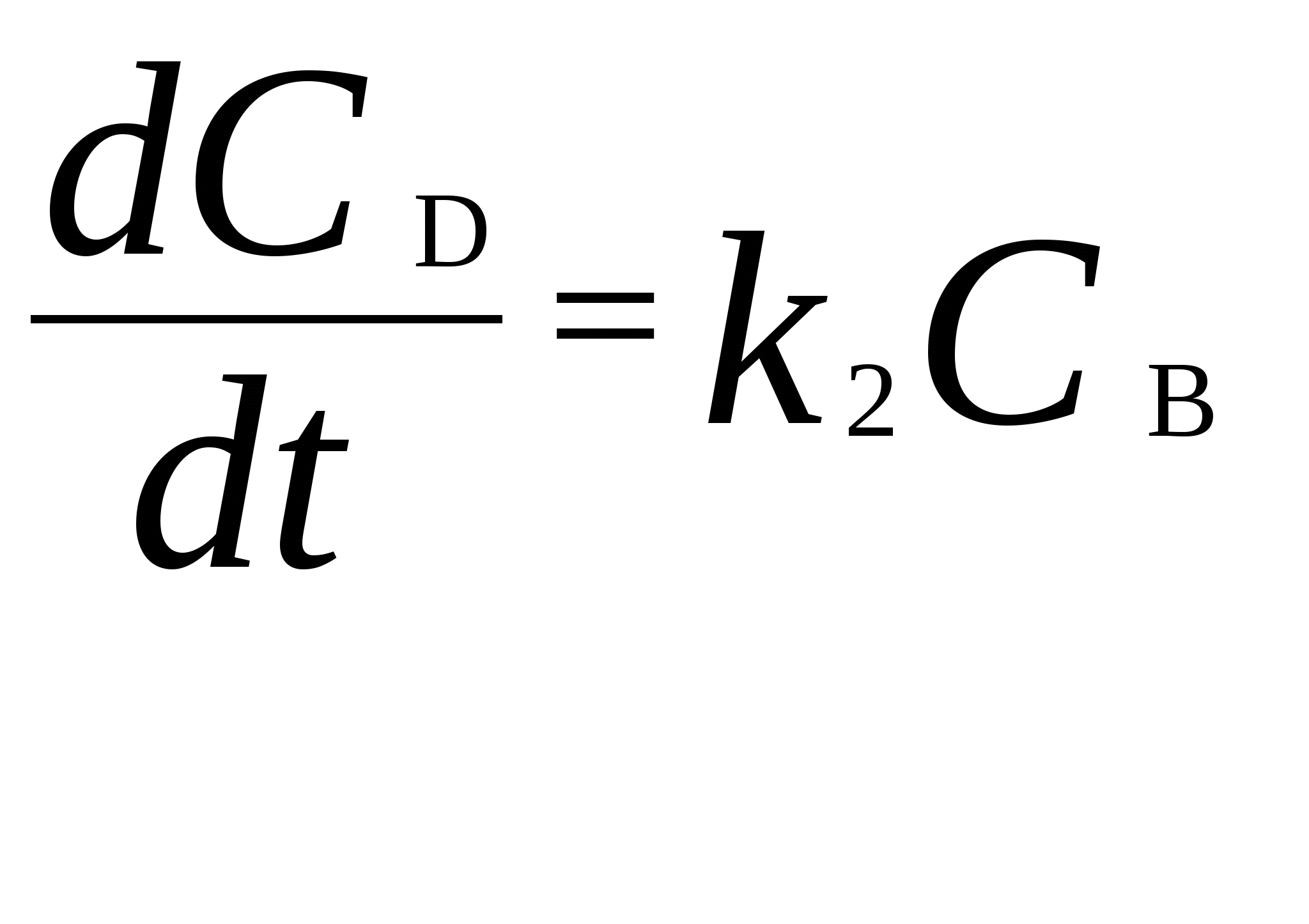

, , .

Решение этих уравнений приводит к следующим результатам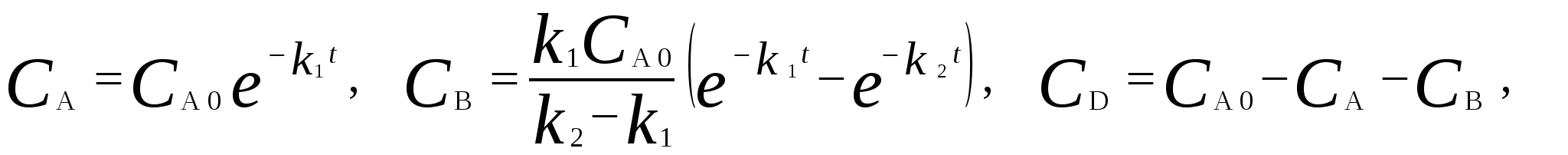

где С _А, С _B , С _D – текущие концентрации веществ А, В и D; С _{А 0} – начальная концентрация вещества A; k ₁ и k ₂ – константы скоростей первой и второй стадий.

Точка максимума на кинетической кривой С _B = f (t) характеризуется уравнениями: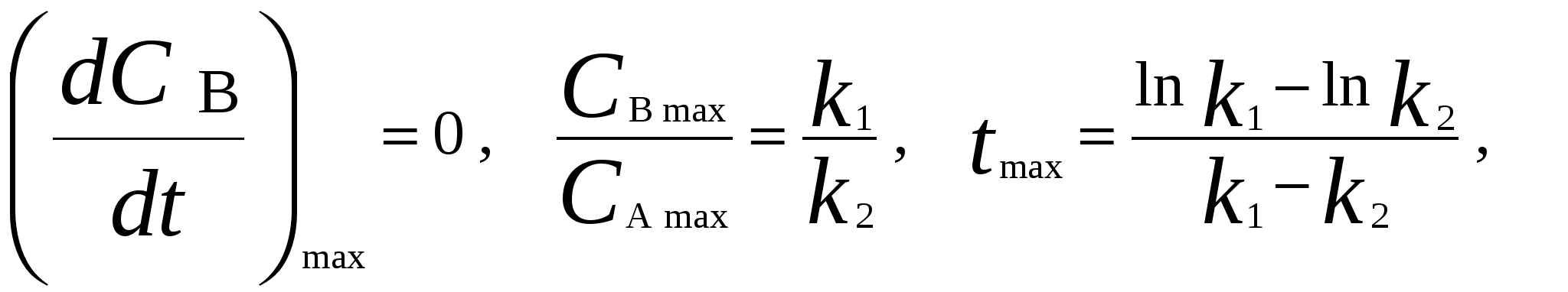



где t _max – время, соответствующее максимальной концентрации вещества B.

Приближенные методы химической кинетики

В сложных реакциях с участием активных промежуточных частиц используется метод квазистационарных (или стационарных) концентраций. В этих реакциях за малый промежуток времени (мало изменение концентрации исходных веществ) в системе устанавливается режим, при котором разность скоростей образования r _o и расходования r _p промежуточных частиц становится малой по сравнению с этими скоростями. Такой режим процесса называется квазистационарным, а соответствующие ему концентрации промежуточных частиц - квазистационарными концентрациями. В квазистационаром режиме можно полагать: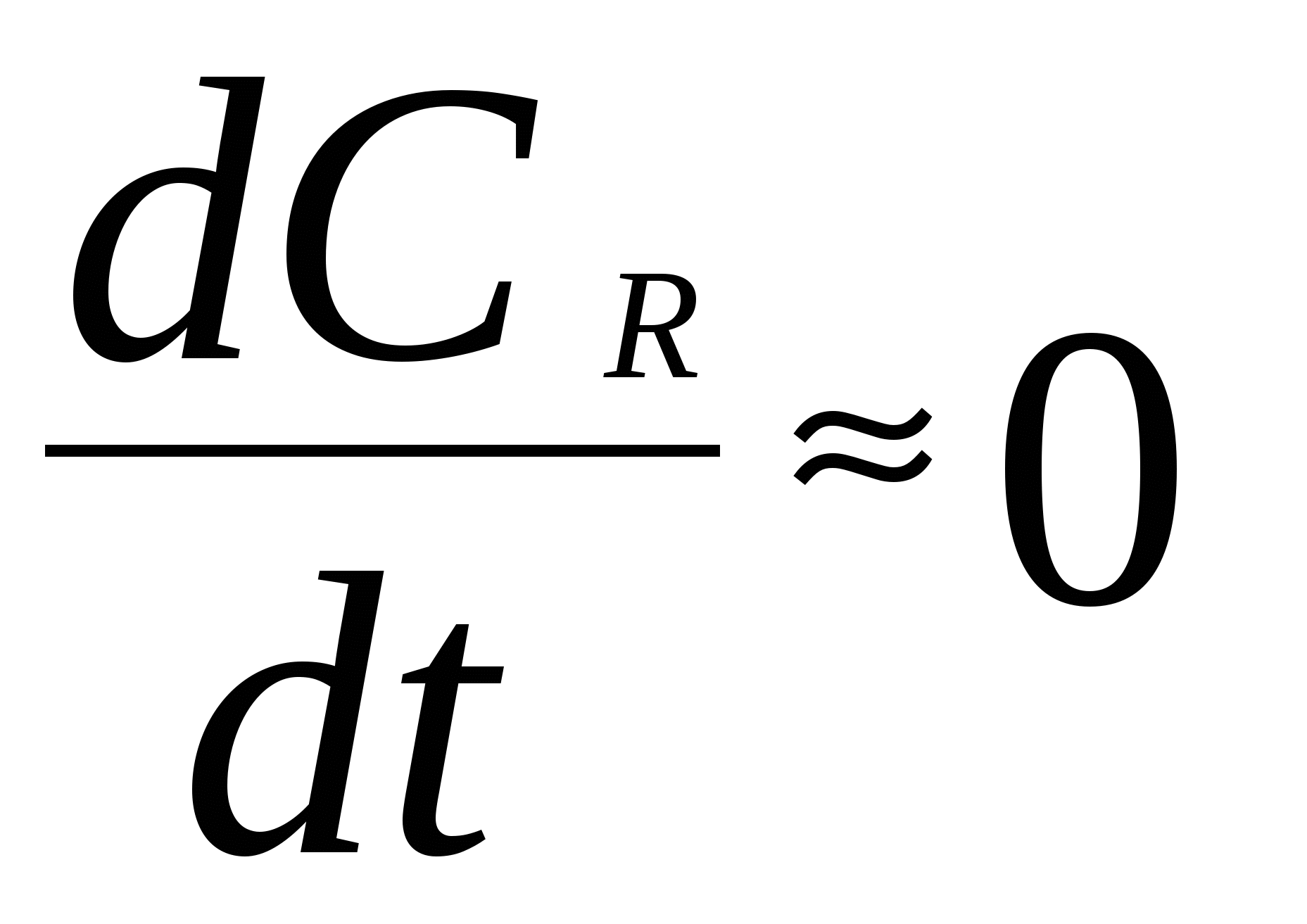

,

где - концентрация промежуточных частиц. В
результате можно выразить концентрации промежуточных частиц через концентрации стабильных веществ, принимающих участие в данном процессе. Если время установления квазистационарного режима мало, концентрации активных промежуточных частиц будут непрерывно подстраиваться к новым квазистационарным значениям, то есть квазистационарный режим не будет нарушаться на протяжении всего процесса. Таким образом, метод квазистационарных концентраций состоит в том, что в системе дифференциальных уравнений, описывающей сложный химический процесс, дифференциальные уравнения для активных промежуточных частиц заменяются алгебраическими уравнениями, выражающими равенство скоростей образования и расходования этих частиц. Метод квазистационарных концентраций применяется обычно к реакциям с участием свободных радикалов, которые представляют собой реакционноспособные неустойчивые частицы.

Квазиравновесное приближение применяют тогда, когда одна из реакций является обратимой, причем равновесие быстро устанавливается и медленно разрушается. Рассмотрим кинетическую схему:

1. A  B ; (k ₁ , k _{– 1} )

2. B  C . (k ₂ )

Поскольку равновесие на первой стадии устанавливается быстро, то k ₂  k _{– 1}. Тогда концентрацию промежуточного продукта В можно выразить через константу равновесия: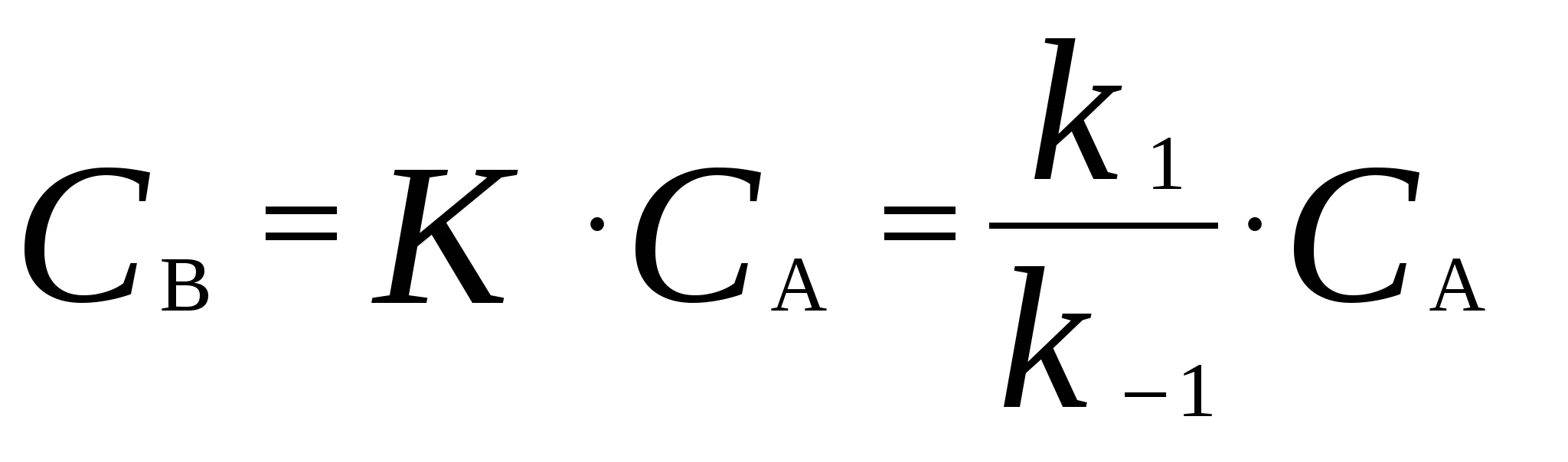

.

Скорость реакции равна: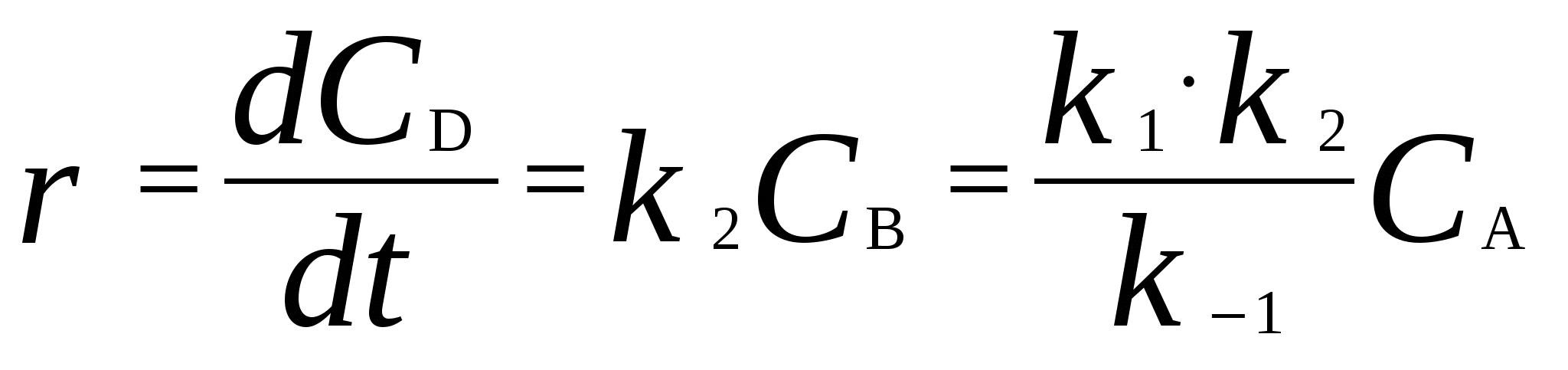

.

Мы получили уравнение реакции первого порядка.

Пример 16. Для обратимого процесса А  В константы скоростей прямой и обратной реакций равны соответственно k ₁ = 0,4 c ^{– 1} , k ₂ = 0,05 c ^{– 1}. Начальные концентрации веществ А и В равны 0,04 моль/л. Определить какими окажутся концентрации этих веществ через 0,2 с.

Решение.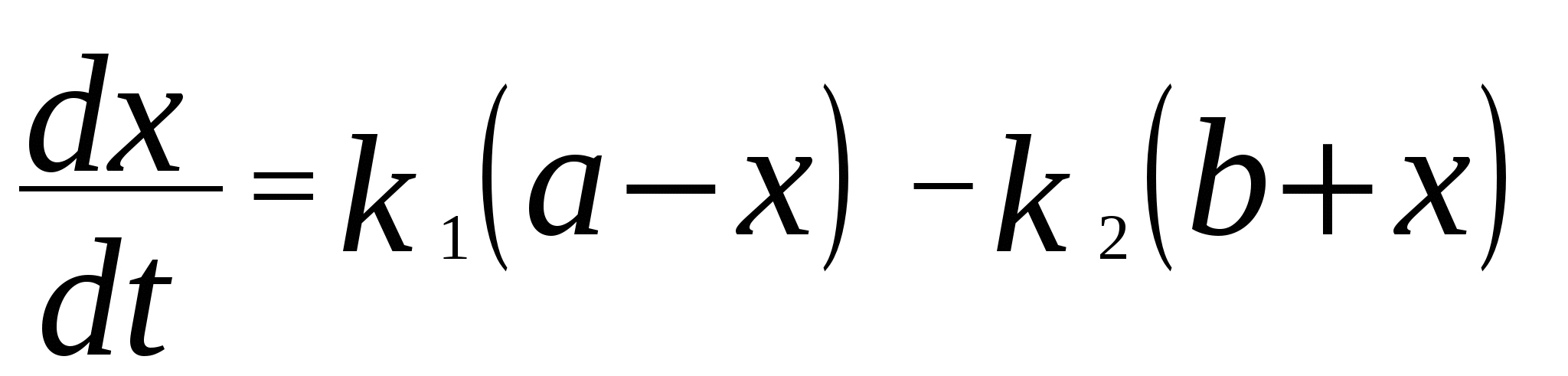

,

где x – количество прореагировавшего вещества А, a и b – начальные концентрации веществ А и В. Решение этого уравнения: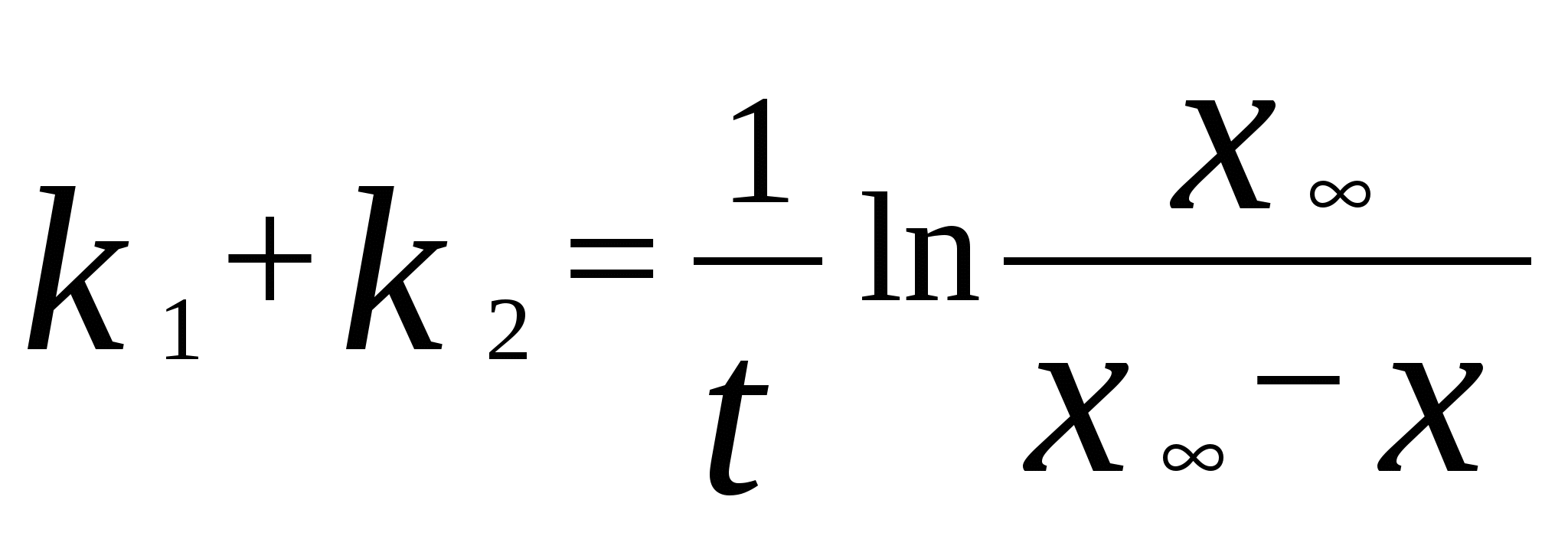

. (*)

Здесь 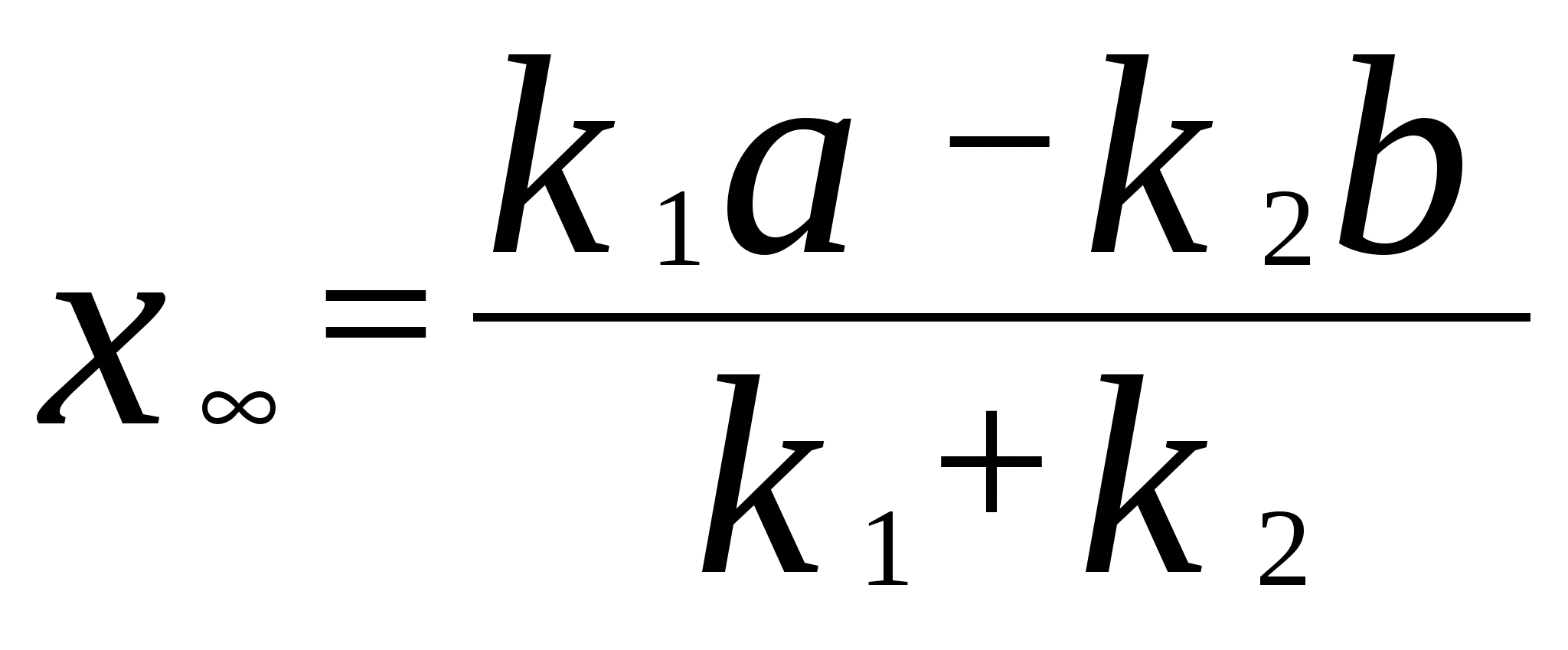- количество прореагировавшего вещества А к моменту равновесия – равно

.

При t   наступает равновесие, которое характеризуется константой равновесия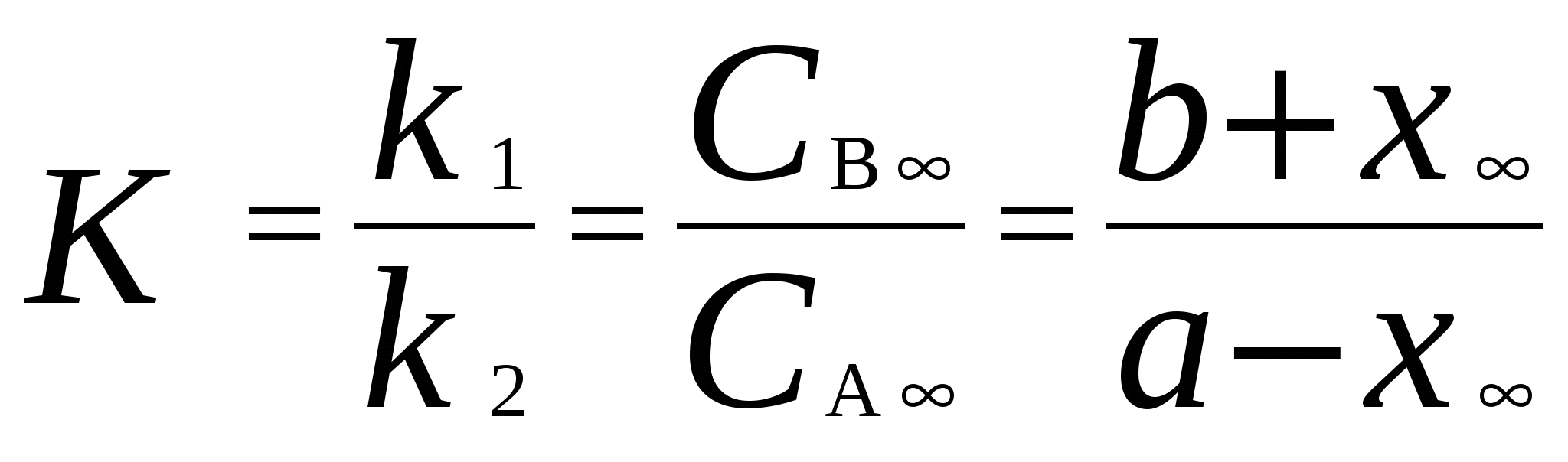

.

Вычисляем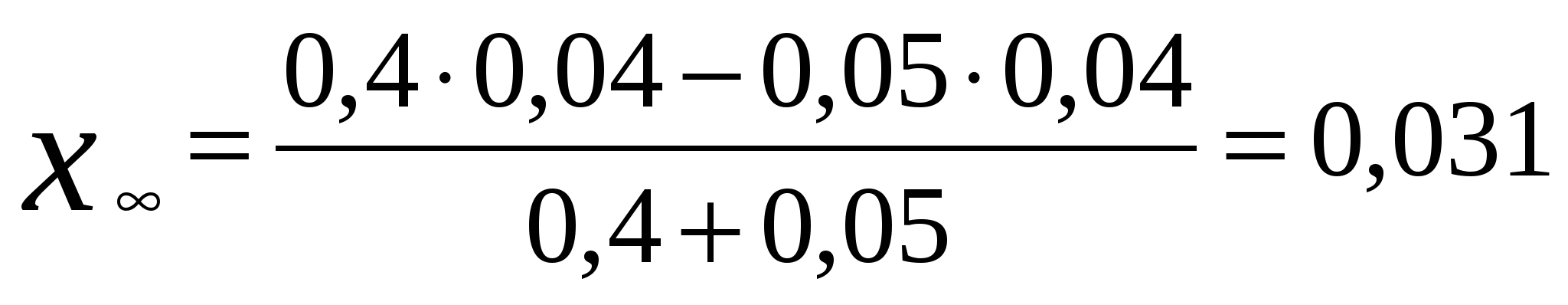

моль/л

Из уравнения (* ) получаем

моль/л;

С _А = 0,04 – 0,0027 = 0,0373 моль/л;

С _В = 0,04 + 0,0027 = 0,0427 моль/л.

Пример 17. В параллельных реакциях первого порядка: 1. А  В ; (k ₁ )

2. A  D ; (k ₂ )

Выход вещества В равен 40 %, а время превращения А на 30 % равно 5 мин. Найти k₁ и k₂.

Решение. Кинетическое уравнение для превращения вещества в двух параллельных реакциях первого порядка имеет вид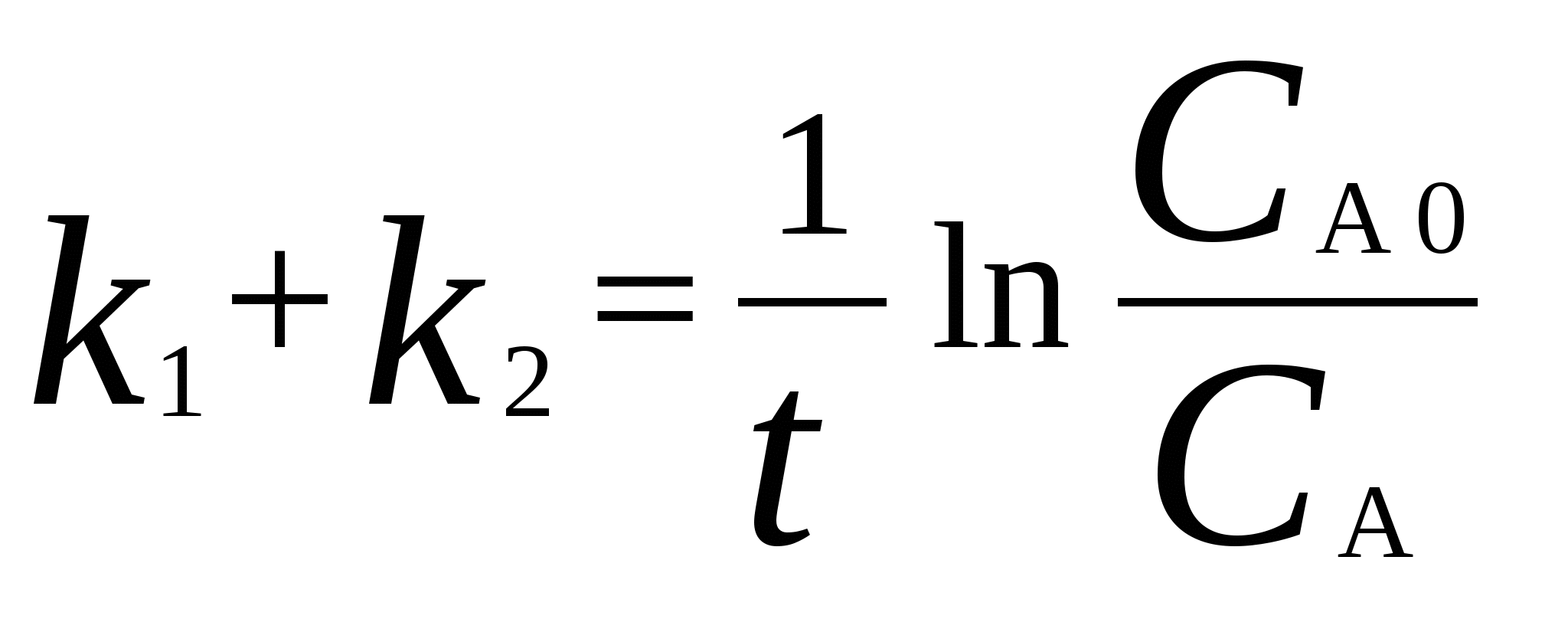

.

С учетом превращения вещества А на 30 % получаем уравнение:

,

где а – начальная концентрация вещества А. Вычисляем

.

Выход вещества В равен 40 %, следовательно выход вещества D – 60 %. Отношение этих выходов равно отношению конечных концентраций веществ В и D. Следовательно, отношение соответствующих констант скоростей равно: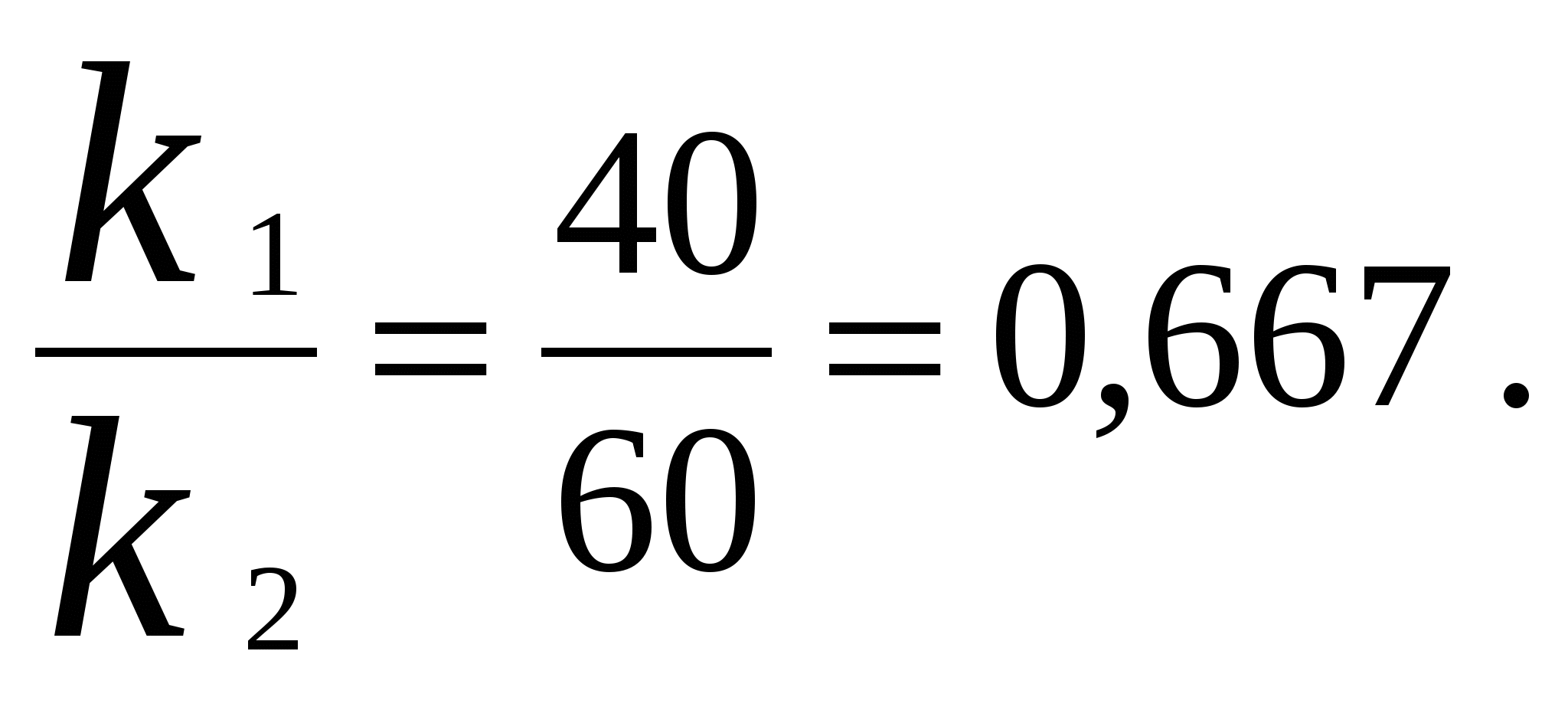



Решаем систему уравнений:

k ₁ = 0,667 k ₂ , k ₁ + k ₂ = 0,071.

0,667 k ₂ + k ₂ = 0,071 ; k ₂ = 0,043 мин ^{– 1}; k ₁ = 0,028 мин ^{– 1} .

Пример 18. В системе осуществляется последовательная реакция

.

Начальная концентрация вещества А равна 1 моль/л, вещества В и D в начальный момент в системе отсутствуют. Константы скорости равны k ₁ = 0, 2 мин ^{– 1} и k ₂ = 0, 05 мин ^{– 1} . Вычислите: 1) время достижения максимальной концентрации вещества В; 2) максимальную концентрацию вещества В; 3) время достижения концентрации С _А = 0,01 моль/л.

Решение. 1. Рассчитаем время, которое будет соответствовать максимальной концентрации промежуточного вещества В: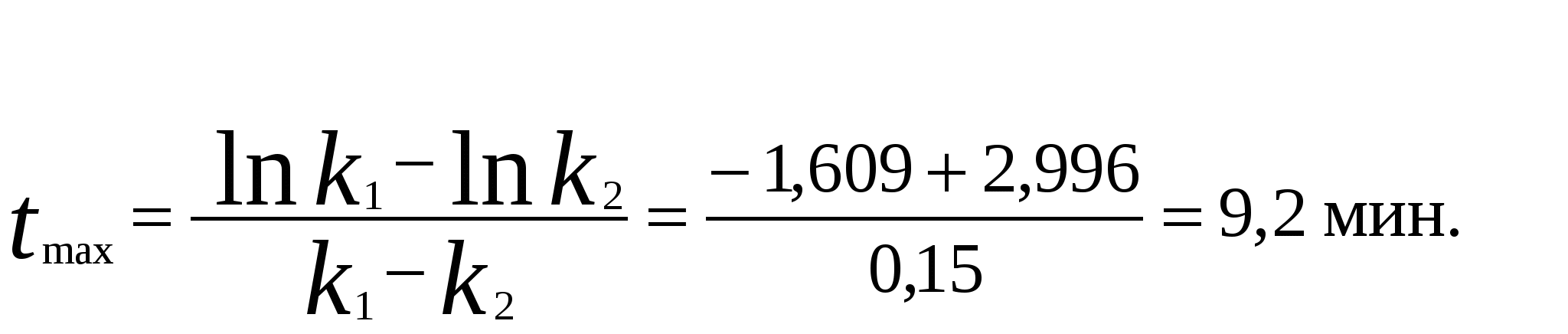



2. Рассчитаем концентрацию вещества А через время t _max: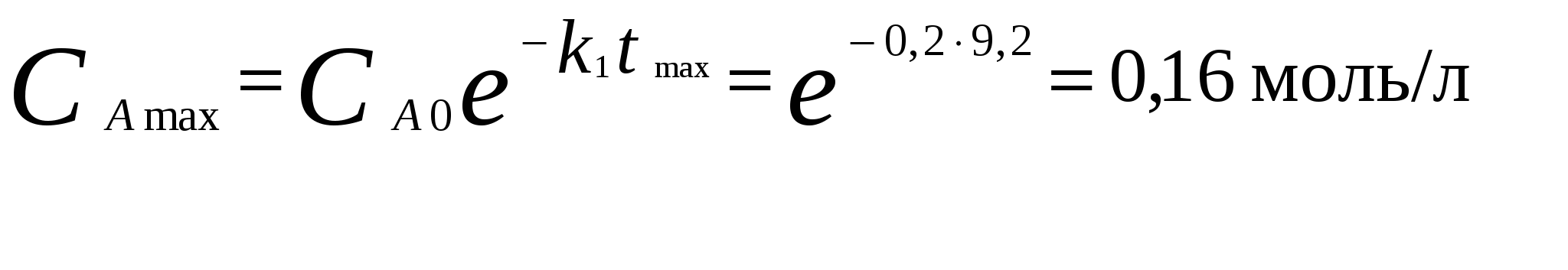

.

Максимальная концентрация промежуточного вещества равна: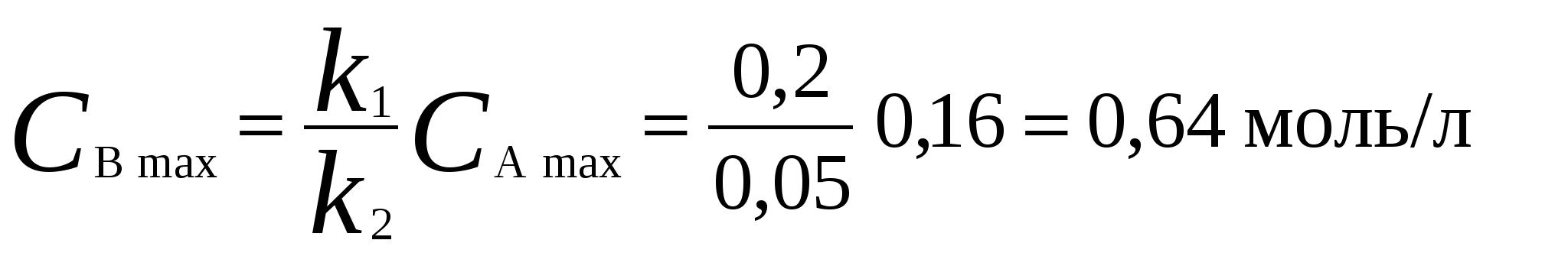



3. Рассчитаем время t _x достижения концентрации С _А = 0,01 моль/л:



Пример 19. Реакция превращения пара-водорода в орто-водород протекает по следующему механизму (М – инертная частица):

1. п-Н ₂ + М  Н + Н + М ;

2. Н + п-Н ₂  Н + о-Н ₂ ;

3. Н + Н + М  п-Н ₂ + М .

Пользуясь методом квазистационарных концентраций, получить выражение для скорости конверсии пара-водорода.

Решение. Из уравнения (2) следует, что скорость образования орто-водорода равна:

.

Метод квазистационарных концентраций применяем для активных атомов водорода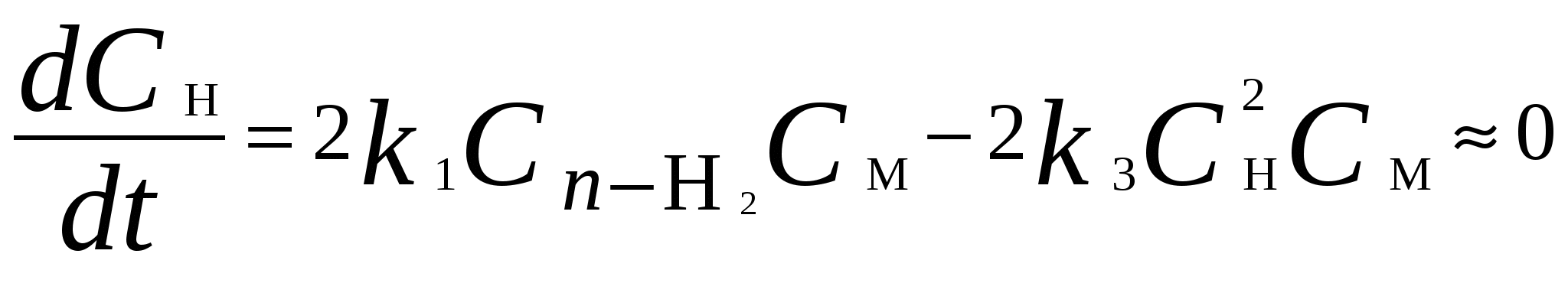

.

Из этого выражения следует, что .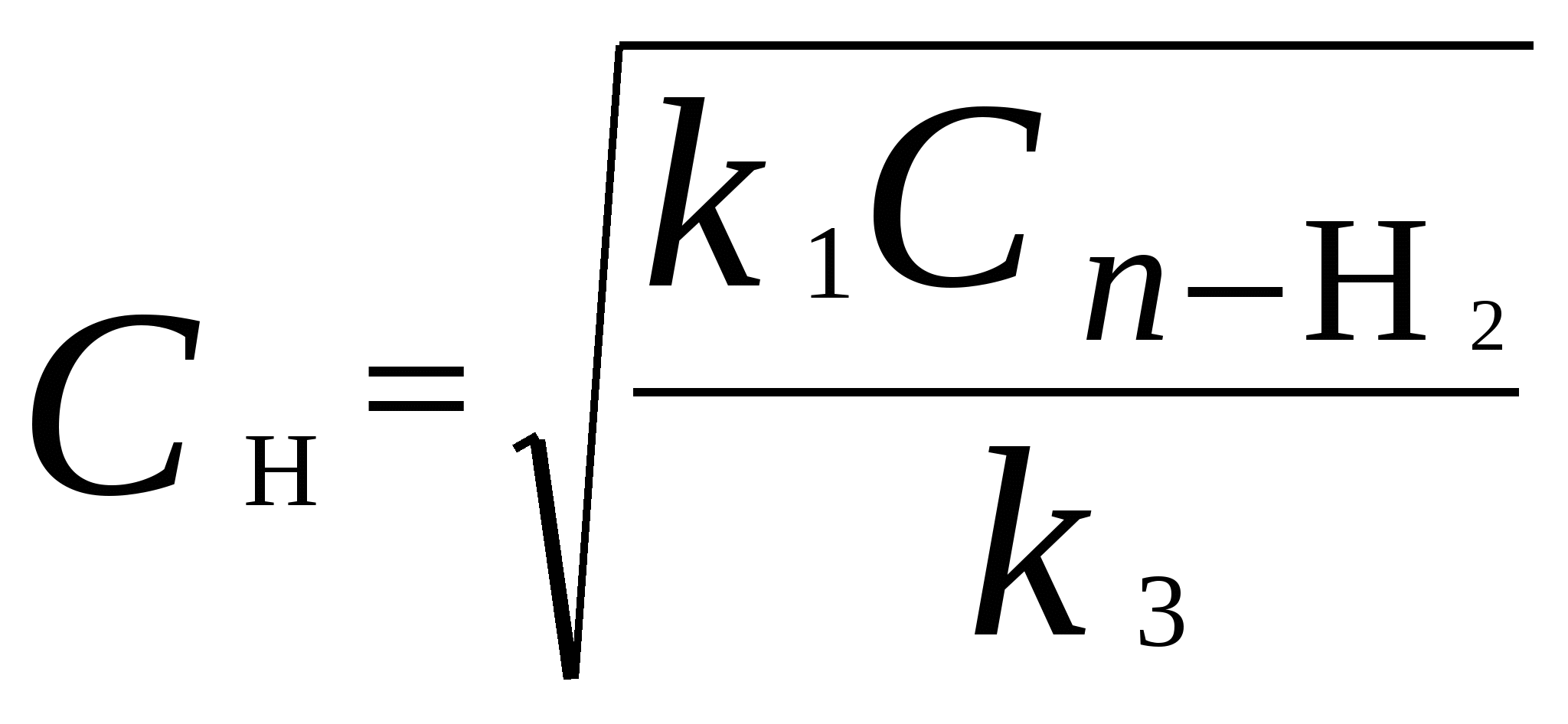

Заметим, что в реакции (2) число атомов Н не изменяется, поэтому скорость изменения их концентрации определяется первой и третьей реакциями. Таким образом, получаем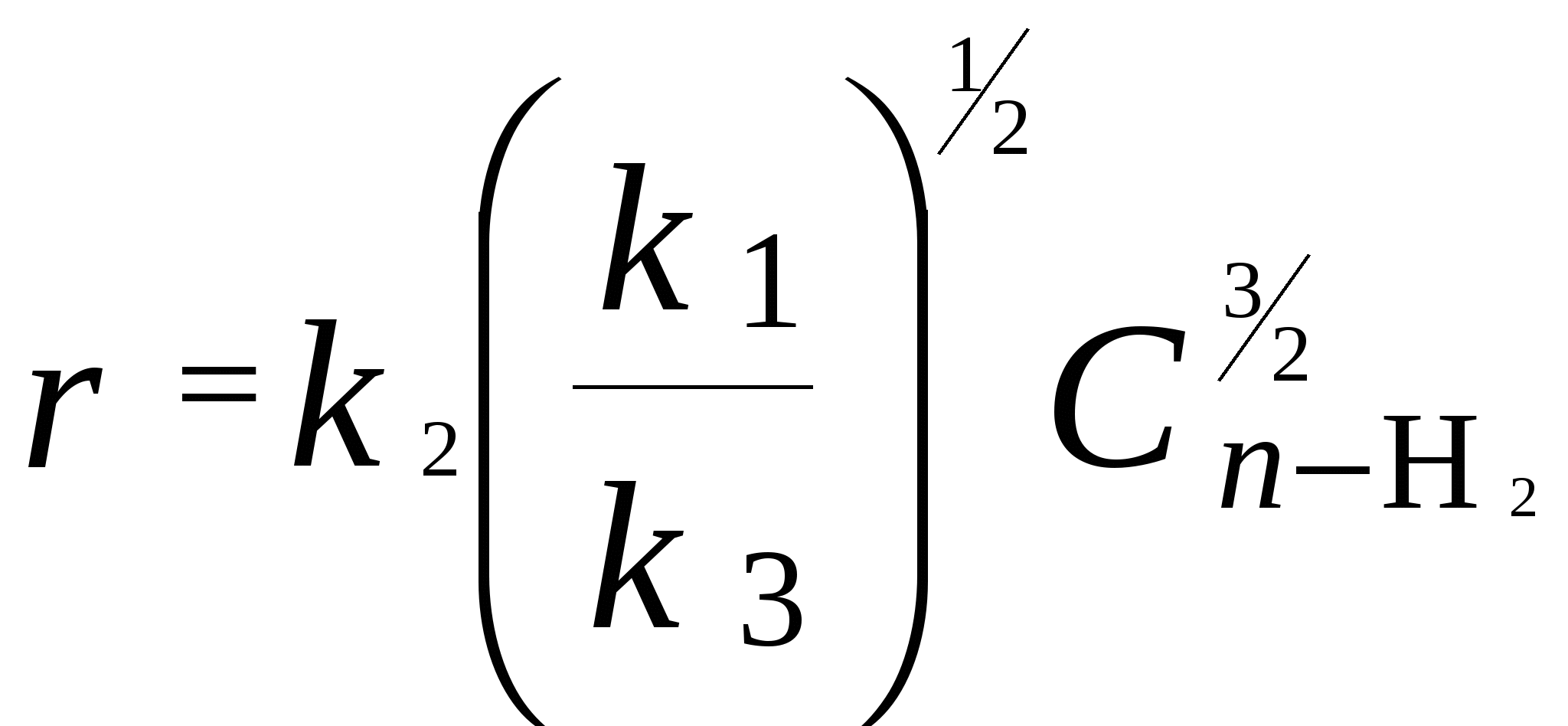

.

Задачи

163. Для обратимого процесса А  В константы скоростей прямой и обратной реакций равны соответственно k ₁ = 0,01 c ^{– 1} и k ₂ = 0,15 c ^{– 1}. Начальные концентрации веществ А и В взяты равными 0,2 моль/л. Определить концентрации этих веществ через 8 с.

164. Константа равновесия обратимой реакции А  В равна 10, а константа скорости прямой реакции равна 0,2 с ^{– 1}. Определить время, за которое концентрации обоих веществ достигнут равенства, если вначале в системе содержалось только вещество А.

165. Для обратимой реакции А  В начальные концентрации веществ равны С _A0 =

= 0,4 моль/л и С _В0 = 0. Через 10 мин после начала реакции С _A = 0,15 моль/ л и С _В =

= 0,25 моль/ л. Определить концентрацию вещества А через 20 мин, если константа равновесия реакции равна K = 3.

166. Константа скорости гомогенного мономолекулярного процесса цис-транс-изомеризации бутена при 417 ⁰С равна 1,6 ^. 10 ⁶ с ^{– 1}. Константа равновесия при этой температуре равна 1,14. В начальный момент времени в системе присутствует только цис-изомер. Вычислить время достижения равных концентраций изомеров.