ЗАДАНИЕ ПО ЭЛЕКТРОТЕХНИКЕ. Методические указания к выполнению индивидуальных работ
 Скачать 166.8 Kb. Скачать 166.8 Kb.
|
|
Методические указания к выполнению индивидуальных работ Индивидуальные работы являются необходимой составляющей учебного процесса. При выполнении работы студент должен обратиться к конспекту лекций и учебной литературе, чтобы осознанно определить набор алгоритмов, расчетных методов и формул. Каждая работа должна содержать постановку задачи и исходные данные варианта, расчет и аналитическую запись расчетных величин. Все расчетные физические величины должны иметь названия с указанием их размерности. При выполнении расчетов в исходные формулы должны быть в явном виде поставлены числовые значения используемых величин. Работы помимо расчетов включают в себя аналитическую запись (без численных значений) электромагнитных волн в заданных условиях и плотности потока мощности, переносимой волной. При расчете параметров электромагнитных волн в заданной среде необходимо вычислить тангенс угла диэлектрических потерь на заданной частоте. По его величине в ряде вариантов можно будет воспользоваться упрощенными формулами в диэлектрических средах с малыми потерями или в хорошо проводящих средах. При аналитической записи электромагнитной волны круговой поляризации воспользуйтесь записью магнитного поля через электрическое поле и характеристическое сопротивление. Учтите, что из четырех поперечных к направлению распространения компонентов векторов поля, один компонент имеет знак минус. Используя аналитическую запись волны, покажите в прямоугольной системе координат, что вектор напряженности электрического поля вращается в сторону отстающей по фазе составляющей при заданной поляризации. При аналитической записи средней за период колебаний плотности потока мощности учтите, что эта величина всегда положительная. При вычислении энергии, теряемой на заданной площади проводника, воспользуйтесь темой «Приближенные граничные условия Леонтовича. Мощность потерь в проводниках». Каждая работа должна быть написана и оформлена грамотно и аккуратно с обязательным титульным листом (прилагается). ФГАОУ ВО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина» Институт радиоэлектроники и информационных технологий – РтФ Департамент радиоэлектроники и связи «Название работы» по дисциплине «Электродинамика и распространение радиоволн» Вариант: M= , N= , L= Доцент департамента радиоэлектроники и связи Соловьянова И.П. Студент гр. РИ – 290006 Дата сдачи Екатеринбург 2021 РАБОТА №1 Расчет параметров электромагнитной волны круговой поляризации в среде с заданными электродинамическими параметрами. Постановка задачи и исходные данные для индивидуальных вариантов Плоская однородная электромагнитная волна правой круговой поляризации распространяется в водной среде в заданном направлении. Вычислить на заданной частоте её параметры: длину волны, коэффициент фазы, коэффициент затухания в дБ/м, модуль и фазу (в градусах) характеристического сопротивления, фазовую скорость. Записать в аналитическом виде комплексные амплитуды, мгновенные значения векторов поля и среднюю за период плотность потока мощности волны правой круговой поляризации в воздушной среде. Номер варианта определяется двумя индексами L и N. Индекс L принимает значения 0; 25; 50; 75. Индекс N- 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Оба индекса определяются по двум последним цифрам номера студенческого билета. Обозначим это число – Х. Индекс L находится через оператор Е выделения целой части следующим образом: 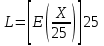 Затем определяется разница (Х-L) и последняя цифра разности равна индексу N. Пример. Х=62, выбирается L=50, разность 62-50=12, отсюда N=2. Если разница (Х-L) однозначное число, то оно и составит индекс N. Исходные данные к задаче приведены в таблицах.
Относительная магнитная проницаемость водной среды =1. РАБОТА №2 Расчет параметров, коэффициентов отражения и преломления плоской электромагнитной волны, падающей по нормали на границу воздуха с проводником. Определение энергии, теряемой на заданной площади проводника. Постановка задачи и исходные данные для индивидуальных вариантов Плоская однородная монохроматическая волна с частотой f падает по нормали на плоскую границу раздела воздуха с проводником. Амплитуда вектора напряженности электрического поля равна Е0. Определить: длину волны и фазовую скорость волны в воздухе и проводнике; модуль и фазу (в градусах) характеристических сопротивлений воздуха и проводника; глубину проникновения волны в проводник; модуль и фазу (в градусах) коэффициентов отражения и преломления; энергию, теряемую на участке проводника с площадью S за время t. записать в аналитическом виде комплексные амплитуды и мгновенные значения векторов суммарного (интерференционного) поля падающей и отраженной волн и среднюю за период колебаний плотность потока мощности, считая проводник идеальным проводником. Номер варианта определяется тремя индексами M, N, L по двум последним цифрам номера студенческого билета. Обозначим это число-Х. Через оператор Е выделения целой части эти индексы вычисляются следующим образом: 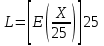 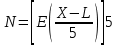 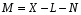 Исходные данные к задаче приведены в таблицах.
Относительные диэлектрическая и магнитная проницаемости всех проводников равны единице. 1.1. Классификация электромагнитных волн по диапазону частот В соответствии с Регламентом радиосвязи, принятым Международным Консультативным Комитетом по Радио (МККР в 1992г. преобразован МСЭ-R сектор радиосвязи Международного Союза Электросвязи) радиоволны разделены на диапазоны. Такое разделение на диапазоны было предложено на заседании IV международного комитета по радиосвязи и телевидению (Бухарест, 1937 г.) и утверждено в 1947 году на международной конференции по радиосвязи в Атлантик-Сити, США (Recommendation ITU-R v.431-7 «Nomenclature ofthefrequencyandwavelengthbandsusedintelecommunications»). Диапазоны радиоволн
Приведенные диапазоны длин волн называются: сверхдлинные волны (СДВ), длинные волны (ДВ), средние волны (СВ), короткие волны (КВ), метровые волны (МВ), дециметровые волны (ДМВ), сантиметровые волны (СМВ), миллиметровые волны (ММВ), децимиллиметровые волны (ДММВ). Соответствующие им частотные диапазоны называются: очень низкие частоты (ОНЧ), низкие частоты (НЧ), средние частоты (СЧ), высокие частоты (ВЧ), очень высокие частоты (ОВЧ), ультравысокие частоты (УВЧ), сверхвысокие частоты (СВЧ), крайне высокие частоты (КВЧ), гипервысокие частоты (ГВЧ). Гипервысокие частоты были добавлены в радиодиапазон относительно недавно. Диапазоны волн от метровых до миллиметровых относят к ультракоротким волнам. Английские названия диапазонов частот полностью аналогичны русским: Very Low Frequencies, Low Frequencies, Middle Frequencies, High Frequencies, Very High Frequencies, Ultra High Frequencies, Extremely High Frequencies, TeraHertz Frequencies. Распределение частот между радиослужбами в диапазоне частот от 9 кГц до 275 ГГц в Российской Федерации утверждено постановлением Правительства № 439–23 от 15.07.2006. Существуют и внесистемные обозначения частотных диапазонов, например, АМ (радиовещание с использованием амплитудной модуляции – от 522 кГц до 1611 кГц), FM (радиовещание с использованием частотной модуляции – от 87,5 МГц до 108 МГц). Каждый частотный диапазон имеет свои особенности распространения, но резких отличий в изменении условий распространения радиоволн на границах соседних диапазонов не существует. Радиотехника развивается с неуклонной тенденцией к освоению все более высокочастотных диапазонов. Это связано с необходимостью создавать высокоэффективные антенные системы, концентрирующие энергию в пределах узких телесных углов. Антенны с узкой диаграммой направленности должны иметь поперечные размеры, многократно превышающие рабочую длину волны. Сделать зеркальную антенну размером 40λ гораздо проще в миллиметровом диапазоне, чем в дециметровом. На более высоких частотах легче сделать высокоскоростные каналы связи. Кроме того, в высокочастотных диапазонах удается проще реализовать большое число радиоканалов с взаимно не пересекающими полосами частот. До диапазона инфракрасных волн процессы распространения, излучения и поглощения электромагнитных волн описываются законами классической электродинамики. На более высоких частотах доминируют процессы, имеющие квантовую природу и в диапазоне оптического и тем более рентгеновского и -излучения процессы могут быть описаны только на основе дискретных представлений. Анализом этих явлений занимается квантовая электродинамика. Список литературы 1. Соловьянова И.П. Теория волновых процессов. Электромагнитные волны. Учебное пособие / И.П. Соловьянова, М.П. Наймушин. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 131 с. 2. Соловьянова И.П. Электродинамика и распространение радиоволн. Учебник УрФУ/ И.П. Соловьянова, Ю.Е. Мительман, С.Н. Шабунин. Екатеринбург: Издательство Уральского Университета, 2020. 412с. 3. Вольман В.И. Техническая электродинамика / В.И. Вольман, Ю.В. Пименов, А.В. Муравцев. М.: Связь, 2000. 480с 4. Сборник задач по курсу” Электродинамика и распространение радиоволн” / Под ред. С.И. Баскакова. М.: Высшая школа. 1981. 208с. 1. Элементы векторного анализа 1.1. Краткие теоретические сведения. Если в каждой точке пространства M ставится в соответствие скалярная величина 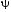 , то говорят о скалярном поле , то говорят о скалярном поле 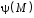 , например поле давлений или поле упругих напряжений. Если точка М имеет декартовы координаты (x, y, z), скалярное поле можно записать в виде , например поле давлений или поле упругих напряжений. Если точка М имеет декартовы координаты (x, y, z), скалярное поле можно записать в виде 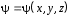 . Наглядно скалярное поле можно изобразить с помощью поверхностей равного уровня. Уравнение поверхностей равного уровня . Наглядно скалярное поле можно изобразить с помощью поверхностей равного уровня. Уравнение поверхностей равного уровня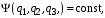 где 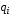 - координатные оси. - координатные оси.Если в каждой точке пространства M ставится в соответствие вектор 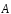 , то говорят о векторном поле , то говорят о векторном поле 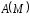 . Например, электрическое поле имеет векторный характер. . Например, электрическое поле имеет векторный характер.Представление вектора в ортогональной системе координат  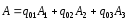 , ,где 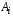 – проекция вектора – проекция вектора 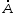 на координатные оси на координатные оси 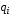 ; ;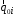 – орты вдоль координатных осей – орты вдоль координатных осей 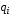 . .Скалярное произведение векторов 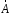 и и 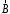 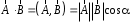 , ,где 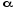 – угол между векторами – угол между векторами 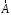 и и 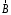 . .В декартовой системе координат 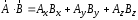 , ,где Аx, Bx, Ay, By, Az, Bz – проекции векторов 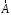 и и 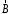 на оси x, y, z . на оси x, y, z .Векторное произведение векторов 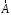 и и 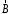 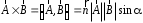 , ,где 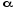 – угол между векторами – угол между векторами 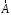 и и 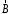 ; ;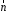 – единичный вектор нормали к плоскости векторов – единичный вектор нормали к плоскости векторов 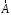 и и 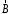 , причём , причём 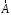 , , 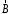 и и 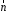 образуют правую тройку векторов. образуют правую тройку векторов.В декартовой системе координат 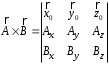 , ,где 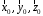 – орты декартовой системы координат. – орты декартовой системы координат.Векторно-скалярное (смешанное) произведение векторов 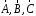 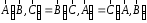 . .Двойное векторное произведение векторов 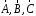 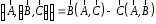 . .Наглядно векторное поле можно изобразить с помощью силовых линий. Силовые линии векторного поля – пространственные кривые, в каждой точке которых вектор поля направлен вдоль касательной. Там, где интенсивность поля больше, силовые линии проводят чаще и наоборот. Уравнение силовых линий 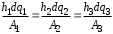 , ,где 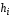 – коэффициенты Лямэ. – коэффициенты Лямэ.Коэффициенты Лямэ для трёх координатных систем: 1. Декартова система координат 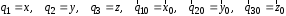 , ,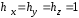 ; ;2. Цилиндрическая система координат 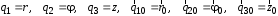 , ,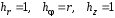 ; ;3. Сферическая система координат 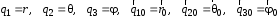 , ,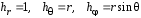 . .Поток векторного поля 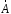 через поверхность S через поверхность S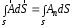 , ,где 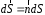 и и 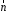 – единичный вектор внешней нормали к площадке dS; – единичный вектор внешней нормали к площадке dS;An– проекция вектора  на нормаль на нормаль 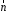 . .Дивергенция (или расходимость) векторного поля  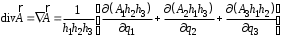 . .Теорема Гаусса-Остроградского: 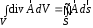 , ,где замкнутая поверхность S охватывает объем V. Циркуляция вектора  вдоль замкнутого контура l вдоль замкнутого контура l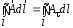 , ,где 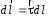 и и 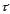 – единичный вектор, касательный к контуру (направление обхода правовинтовое). – единичный вектор, касательный к контуру (направление обхода правовинтовое).Ротор (или вихрь) векторного поля  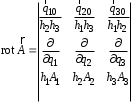 . .Теорема Стокса: 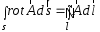 , ,где поверхность S опирается на замкнутый контур l. Градиент от скалярной функции 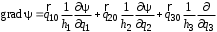 . .Дифференциальный оператор – набла 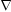 (оператор Гамильтона) (оператор Гамильтона) . .Дифференциальные операции с использованием оператора набла  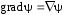 ; ; 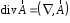 ; ; 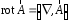 . .Скалярное произведение 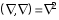 – оператор Лапласа. – оператор Лапласа.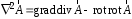 , ,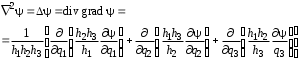 . .Некоторые формулы векторного анализа 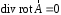 ; ; 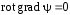 ; ; 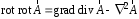 ; ;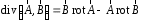 ; ; 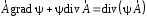 Векторное поле без источников, т.е. с нулевой дивергенцией, называется соленоидальным. Векторное поле 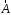 , для которого во всех точках удовлетворяется условие , для которого во всех точках удовлетворяется условие 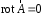 , называется потенциальным. , называется потенциальным. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
