Пневмопривод. Ручкин, Скрипка. Методические указания к выполнению курсового проектирования для студентов

• Название: Методические указания к выполнению курсового проектирования для студентов
• Анкор: Пневмопривод. Ручкин, Скрипка.doc
• Дата: 15.05.2017
• Размер: 6.99 Mb.
• Имя файла: Пневмопривод. Ручкин, Скрипка.doc
• Тип: Методические указания; #7590
• страница: 2 из 10

3.3. Расчет конструктивных параметров
Полезная площадь поршня вычисляется по формуле
(3.8)
где – магистральное давление; Х – безразмерная нагрузка для обеспечения достаточного быстродействия. Ее оптимальные значения выбирают из интервала Х = 0,4….0,5 [1]; Р – предварительное значение полной нагрузки.

Расчетный диаметр поршня D определяем по выражению
(3.9)
Диаметр штока d находят согласно конструктивным параметрам, в пределах d = (0,2 – 0,5)D. Полученные значения D и d округляются до ближайших значений из номинального ряда согласно ГОСТ 12447–80: 8; 10; 12; 14;16; 18; 20; 22; 25; 28; 32; 36; 40; 45; 50; 56; 63; 70; 80; 90; 100; 110; 125; 140; 160; 180; 200; 220; 250; 280; 320; 360; 400. После этого уточняются значения площадей рабочей F₁ и выхлопной F₂ полостей соответственно и вычисляется коэффициент асимметрии полостей цилиндра
П = F₂ / F₁.

Далее уточняется значение полной нагрузки на поршень Р:
P = P₁ + P₂+ P₃, (3.10)
где P₂ – сила трения; P₃ – сила противодавления.

При уплотнении штока и поршня резиновыми кольцами круглого сечения или резиновыми манжетами (воротниками) сила трения определяется по формуле [3]
(3.11)
где D– диаметр уплотняемой поверхности; b– ширина манжеты или кольца; µ – коэффициент трения (µ = 0,13...0,15); n – число манжет или колец уплотнений; р_к – принятое радиальное давление уплотнения (р_к = 0,7 МПа).

Силу противодавления находят по формуле
(3.12)
где – давление в выхлопной полости; – атмосферное давление.

4. РАСЧЕТ ПНЕВМОСИСТЕМЫ
Целью расчета пневмосистемы является определение пропускной способности пневмолиний.

4.1. Расчет расхода воздуха
На начальном этапе определяется необходимый массовый расход воздуха для напорной G_н и выхлопной G_смагистралей.

Для напорной магистрали
(4.1)
где р₁ – давление в напорной полости; F_{1_}− площадь напорной полости; V_max − максимальная скорость; η₀ – объемный КПД двигателя
(η₀ = 0,8….0,95); R– газовая постоянная (R = 287 Дж/кг); Т₁ – температура рабочей среды.

Для выхлопной магистрали
(4.2)

где р₂ – давление в напорной полости; F_{2 _}− площадь напорной полости; V_max− максимальная скорость; η₀ – объемный КПД двигателя
(η₀ = 0,8…0,95); R– газовая постоянная (R = 287 Дж/кг); Т₂ – температура рабочей среды.

4.2. Расчет диаметров условного прохода
Диаметр d_у условного прохода для напорного трубопровода, соответствующий расходу G_ни скорости потока u воздуха, определяется по формуле
(4.3)
где G_H – массовый расход воздуха напорной магистрали; ρ_М – плотность воздуха при рабочих условиях; u − скорость потока воздуха. В первом приближении ее можно принять u = 50 м/с [4].

Плотность воздуха при рабочих условиях определяем по формуле
(4.4)
где ρ₀ – плотность при нормальных условиях (ρ₀ = 1,25 кг/м³); р₀ – давление при нормальных условиях (р₀ = 0,1 МПа); Т₀ – температура при нормальных условиях (Т₀ = 293 К).

Полученные значения d_уокругляются до ближайшего значения из номинального ряда по ГОСТ 16516–80: 1; 1,6; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 63; 80; 100; 125; 160; 200 и т. д. По выбранным значениям d_у уточняют типоразмеры распределителей и регулирующей аппаратуры, потери давления в пневмоаппаратуре, рабочие давления в напорной и выхлопной полостях двигателя.

4.3. Определение потерь давления в пневмолиниях
На следующем этапе определяются потери давления в объемном приводе, которые рассчитываются отдельно для напорной Δр_н и выхлопной Δр_вмагистралей. Различают два вида потерь: потери давления в местных сопротивлениях и потери давления на трение по длине трубопровода.

Общие потери давления на участке магистраль – пневмодвигатель рассчитывают по формуле
(4.5)
где Δp_т – потери давления на трение на участках пневмолиний; Δp_м – потери давления на трение на местных сопротивлениях.

Определяем потери давления на трение по длине трубопровода в напорной магистрали
(4.6)
где λ – коэффициент трения. Его в зависимости от режима течения находят следующим образом:

– если Re < 2 300 – по формуле Пуазейля:
(4.7)
– если Re > 2 300 – по формуле Альтшуля:
(4.8)
где Δ – величина, эквивалентная по своему воздействию на поток равнозернистой шероховатости Δ, значения которой приведены в табл. 4.1.
Таблица 4.1

Характеристика поверхности труб	Δ, мм
Технически гладкие из латуни, меди	0,001 5…0,010
Новые стальные	0,020…0,10
Трубы из чистого стекла	0,001 5…0,010

Число Рейнольдса определяется по формуле
(4.9)
где ν – кинематическая вязкость, которую вычисляют по формуле
(4.10)
Здесь µ – динамическая вязкость воздуха, которую выбирают по табл. 4.2.
Таблица 4.2

t, С	–20	–10	0	10	20	40	60	80	100
	1,59	1,65	1,71	1,77	1,83	1,95	2,07	2,19	2,33

Потери давления Δp_м в местных сопротивлениях рассчитывают по формуле Вейсбаха:
(4.11)

где ξ_м – коэффициент местного гидравлического сопротивления. Его находят по следующим условиям [5]:

– при резком сужении потока
(4.12)
– при внезапном расширении потока
(4.13)
– при постепенном расширении потока (диффузор)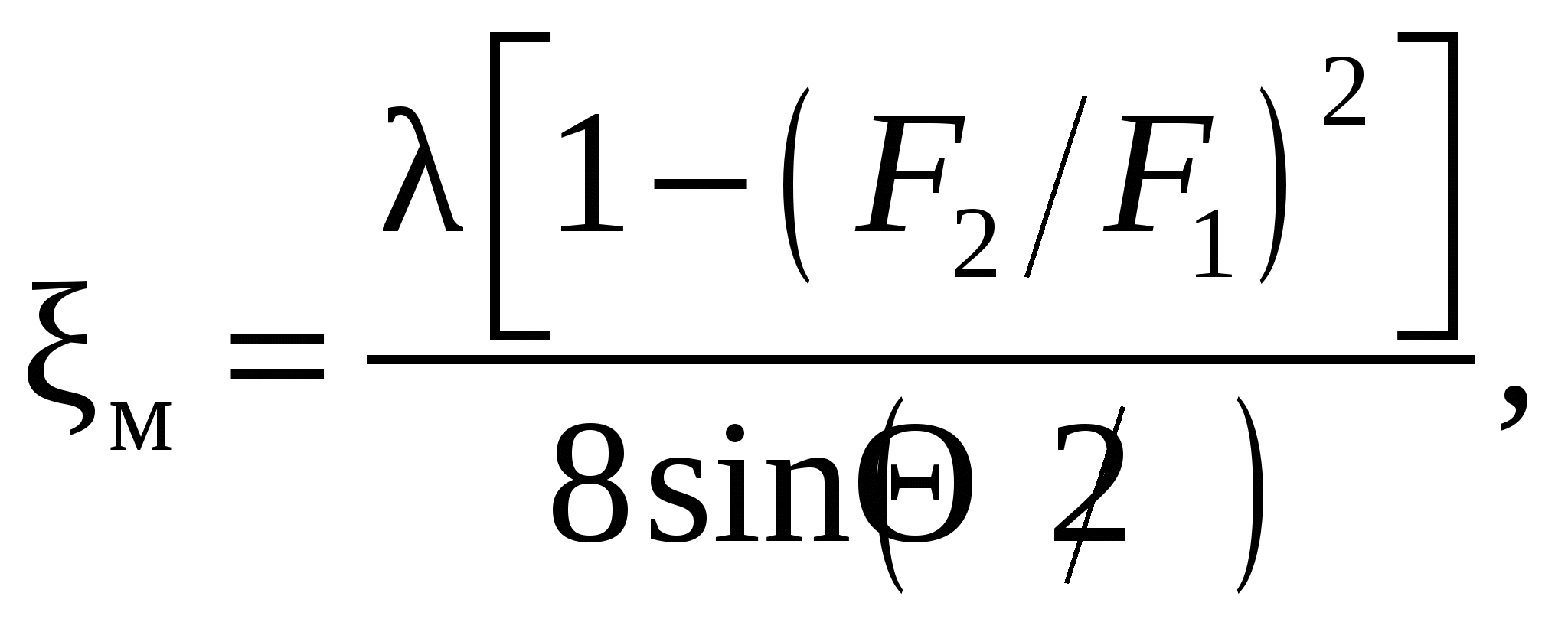
(4.14)
где F₁ и F₂ − сечения потока до местного сопротивления и в местном сопротивлении соответственно; λ − коэффициент трения вычисляется по параметрам потока до диффузора; Θ – угол расширения диффузора.

Суммарные потери Δр_н в напорной магистрали составляют
(4.15)
Эффективную площадь F_э поперечного сечения трубопровода, характеризующую пропускную способность трубопровода, вычисляют по формуле
F_э = µ ·F_у,(4.16)
где µ – коэффициент расхода; F_у– площадь условного прохода.

Затем находят коэффициент расхода: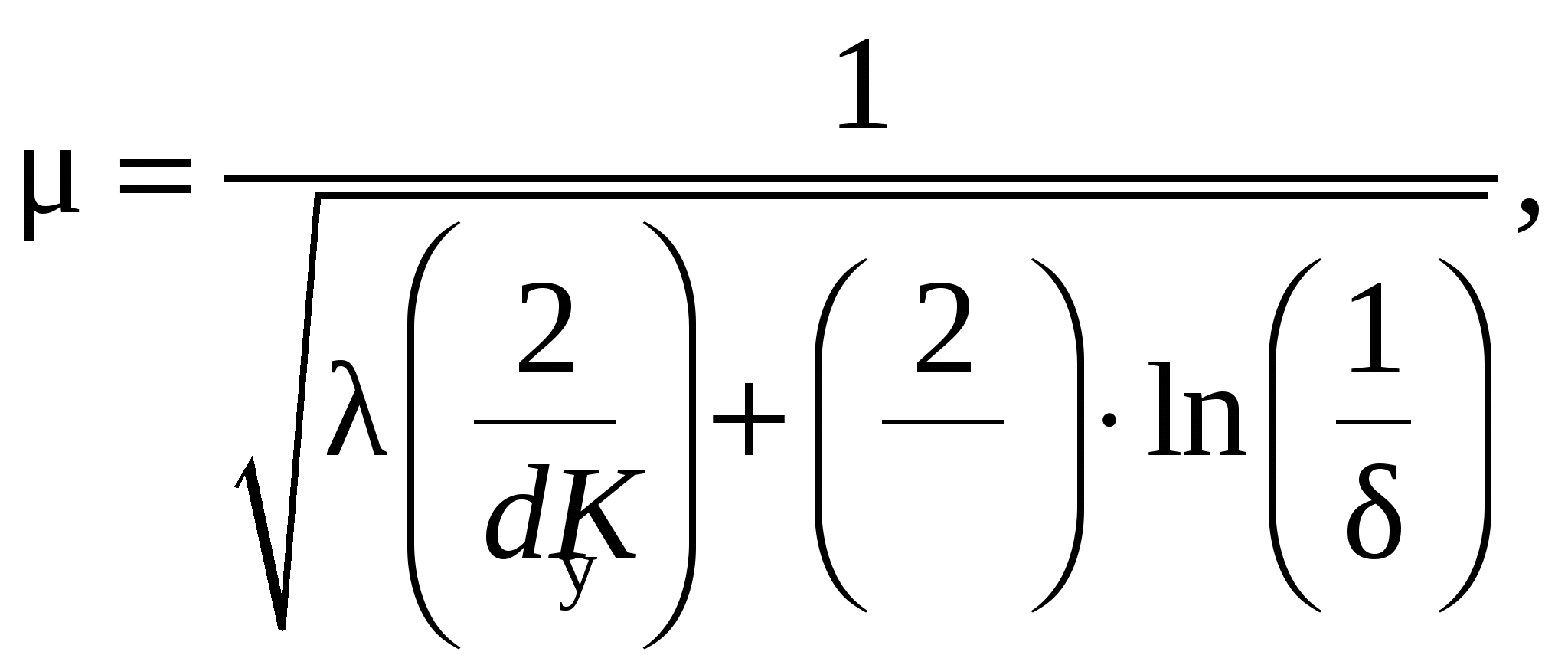
(4.17)
где δ – коэффициент расхода; К – показатель адиабаты (К = 1,4).

Определяем коэффициент расхода для напорной магистрали:
(4.18)
Площадь условного прохода F_у цилиндрического трубопровода равна
(4.19)
Уточняем значение скорости потока:
(4.20)
где µ – коэффициент расхода; р_м – магистральное давление; ρ_М – плотность воздуха при рабочих условиях; δ – коэффициент расхода; К – показатель адиабаты (К = 1,4).

Уточняем массовый расход воздуха G в напорной магистрали:
(4.21)
Объемный расход воздуха Qв начальном сечении:
(4.22)
Максимальный расход воздуха G_max:
(4.23)
где δ^* – критическое отношение давлений (δ^* = 0,528).

На этом этапе целесообразно сравнить полученное значение расхода G_max с пропускной способностью К_v или с номинальным расходом Q_н пневмоаппаратов, представленных в их технических характеристиках.

После этого проверяют максимальную скорость V_maxпневмодвигателя, обеспечиваемую выбранными параметрами пневмолиний и аппаратуры, подставляя полученные значения:
(4.24)
Полученное значение сравнивается со значением, полученным при энергетическом расчете. Параметры пневмосистемы в случае необходимости корректируются, и вновь выполняется расчет.

Затем при дроссельном регулировании, зная пределы измене­ния скорости движения v выходного звена, определяется изменение площади проходного сечения F_дрдросселя по формулам (4.1), (4.2) с учетом условия постоянства массового расхода воздуха. Площадь дросселя F_др= c · x, где х – перемещение регулятора дросселя, с – коэффициент пропорциональности. Для того чтобы обеспечить линейную зависимость массового расхода Gот хода регулятора x, конструкция регулятора должна обеспечить условие с = const.

Обычно режим течения потока воздуха при дросселировании является турбулентным. Ламинарный режим используется в маломощных элементах пневмоавтоматики. В качестве расходной характеристики турбулентного дросселя применяют формулу массового расхода воздуха [10]. В диапазоне 0,9 < δ < 1 изменения давлений можно пренебречь изменением плотности ρ потока и использовать [4] формулу
(4.25)
где µ – коэффициент расхода; р₀ – давление на входе в дроссель; ρ – плотность потока; δ – относительное давление; F_др – площадь дросселя.

Суммарные потери давления для выхлопной магистралиΔр_с вычисляются аналогично напорной.

Затем определяют максимальные рабочие давления в полостях двигателя:
p_1max = р_м – Δр_н;(4.26)
р_2max = р_а + Δр_с. (4.27)
Таким образом, максимальное усилие Р_ц, которое может обеспечить двигатель, рассчитывается по выражению
Р_ц = F₁(p_1max – П · р_2max)·η_м,(4.28)
где η_м – механический КПД двигателя (η_м= 0,8…..0,95).

Максимальное усилие двигателя Р_ц должно превышать полную нагрузку на штоке двигателя Р, т. е. Р_ц > Р.

Если выбранные параметры устраивают разработчика, то на этом этапе заканчивается расчет пневмосистемы, в противном случае задают другие параметры (например, изменяется диаметр условного прохода трубопроводов), и расчет повторяется.

5. РАСЧЕТ ВРЕМЕНИ СРАБАТЫВАНИЯ
Для определения времени срабатывания привода требуется совместное решение дифференциальных уравнений [1], описывающих изменение давлений в рабочей и выхлопной полостях пневмодвигателя, и уравнения движения штока двигателя с приведенной к нему массой.

Уравнения изменения давлений в рабочей и выхлопной полости двигателя имеют вид
(5.1)
(5.2)

где φ(δ_i) – функции расхода, значения которой равны:




х₀₁, х₀₂ – соответственно начальные и конечные координаты поршня;
х – текущее положение поршня.

Уравнение движения поршня под действием постоянных сил Р имеет вид
(5.3)
где Р – результирующая всех сил, приложенных к поршню, кроме сил давления сжатого воздуха.

Система уравнений (5.1), (5.2) и (5.3) решается методами численного интегрирования. При проектировании новых приводов обычно программы решения указанных уравнений на ПК отсутствуют, поэтому из-за высокой трудоемкости решения и приближенности многих параметров (величины коэффициента расхода µ, приведенной массы m_пр, силы полной нагрузки Р и т. п.) целесообразно использовать приближенный метод расчета времени Т_п срабатывания привода.

Время срабатывания привода Т_п состоит из подготовительного времени Т₁, времени Т₂ движения поршня и заключительного времени Т₃.

Подготовительное время Т₁ состоит из времени t₁ срабатывания пневмоклапана, времени t₂ распространения волны давления и времени t₃изменения давления в рабочей полости:
Т₁ = t₁ + t₂ + t₃.(5.4)
Время t₁ приводится в технических характеристиках пневмоклапанов и распределителей.

Время t₂ распространения волны давления от пневмоклапана до двигателя определяется по формуле:
(5.5)
где l – длина трубопровода; u^* – скорость потока.

Время t₃ изменения давления в рабочей полости определяется временем наполнения этой полости от давления р_а до давления р_1д, при котором начинается движение поршня [1]:

(5.6)
где V₀₁ – начальный объем рабочей полости с учетом присоединенных объемов трубопроводов от клапана до двигателя; F_э1 – эффективная площадь сечения трубопроводов; отношение давлений; Ψ₁(δ_1д), Ψ₁(δ_1а) – функции истечения, определяемые как
Ψ₁(δ) = δ,при0 ≤ δ ≤ 0,528
и
, при 0,528 ≤ δ ≤ 1,(5.7)
где – критическое отношение давлений; – функция расхода при k– показатель адиабаты.

Время истечения воздуха из выхлопной полости (до начала движения) определяется по формуле [1]
(5.8)
где V₀₂ – начальный объем выхлопной полости; F₂·s – рабочий объем выхлопной полости двигателя; F_э2– эффективная площадь сечения трубопровода выхлопной линии.

Большее из определяемых величин и и будет составлять подготовительное время t₃. Отметим, что чаще всего большим является время истечения воздуха из выхлопной полости.

При определении времени движения поршня Т₂ рассчитывается величина обобщенного конструктивного параметраN:
(5.9)
где F_э– эффективная площадь поперечного сечения трубопровода;
D – диаметр поршня; Р – полная нагрузка на шток цилиндра; s – рабочий ход; р_м– магистральное давление.

Диапазон конструктивного параметра N будет составлять N= 0,005…5. При наиболее распространенных в машиностроении диапазонах изменения параметров они равны:
µ = 0,2…0,8, D= 0,1…0,3 м, F_у /F₁ = 0,001 5…0,01,

Р = 1…2 000 Н, s = 0,15…2 м, р_м = (3…7) · 10⁵ МПа.
Затем определяют коэффициент пропускной способности пневмолиний . Он изменяется в диапазоне . Для двухстороннего привода коэффициент пропускной способности пневмолиний обычно принимается . Коэффициенты начальных объемов полостей рассчитывают по выражениям:
;
,
где V₀₁иV₀₂ – начальные объемы полостей. Для двустороннего привода обычно коэффициенты начальных объемов равны. Диапазон изменения коэффициента составляет γ≤ 0,3; безразмерная нагрузка отношение давлений .

На следующем шаге находят безразмерное время τ движения поршня привода. Время τвключает подготовительное время t₃ нарастания давления до величины, при которой начнется движение поршня, и непосредственно время Т₂ движения поршня:
при 0 < N < 1, (5.10)
при 1 < N < 5. (5.11)
Указанные выше формулы справедливы при коэффициенте асимметрии полостей цилиндра (П), равном 1.

При 0,5 < П < 1,0 можно использовать формулу


при 1 < N< 5. (5.12)
Если параметры привода выходят за указанные пределы (например N > 5, δ_а < 0,1 и т. д.), необходимо определять время срабатывания привода численным интегрированием системы уравнений изменения давлений в рабочей (5.1), выхлопной (5.2) полостях и уравнения движения поршня(5.3).

Если параметры привода входят в указанные пределы, то определяется действительное время движения поршня привода:
(5.13)
Заключительное время Т₃ находят аналогично вышеизложенному, только при определении времени изменения давлений в полостях двигателя рабочий объем F₁sдобавляется к V₀₁. За начальные параметры заключительного периода δ₁₁ и δ₂₁ принимаются параметры, полученные в результате вычисления времени Т₂ движения поршня, а конечными – давление р_а для выхлопной полости и давление р_М – для рабочей полости. В большинстве случаев для заключительного периода учитывается только время наполнения рабочей полости.