Пневмопривод. Ручкин, Скрипка. Методические указания к выполнению курсового проектирования для студентов

• Название: Методические указания к выполнению курсового проектирования для студентов
• Анкор: Пневмопривод. Ручкин, Скрипка.doc
• Дата: 15.05.2017
• Размер: 6.99 Mb.
• Имя файла: Пневмопривод. Ручкин, Скрипка.doc
• Тип: Методические указания; #7590
• страница: 3 из 10

6. ПРИНЦИП ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
В процессе проектирования пневмоприводов приходится проводить динамический анализ расчетным путем. Однако при индивидуальном подходе к математическому описанию конкретных пневмоприводов и дальнейшем составлении и отладке специальной программы расчета на персональном компьютере (ПК) затраты времени на динамический анализ оказываются чрезмерными. Выходом из такого положения может быть одноразовая разработка и последующее многократное использование для большой группы пневмоприводов обобщенного математического описания и универсальной программы динамического расчета на ПК.

6.1. Динамика пневмопривода
Рассмотрим методику построения полной математической модели на примере манипулятора с пневматическим приводом ведущих звеньев (рис. 6.1).

1

9

11

10

122

Ц12

Ц32

Ц42

2

8

5

6

4

3

7

Ц22

Ц12


Рис. 6.1. Кинематическая схема манипулятора

Манипулятор состоит из ведущих звеньев 1 и 2, смонтированных на приводных валах 3 и 4, на каждом из которых установлены шестерни 5 и 6, сопряженные со шток-рейками 7 и 8 пневмоцилиндров Ц1…Ц4. На звеньях 1 и 2 шарнирно смонтированы ведомые звенья 9 и 10, шарнирно связанные между собой промежуточным звеном 11, на котором установлены схваты 12. Ведомые и ведущие звенья каждой пары кинематически связаны между собой, например, при помощи зубчатых ремней 13.

Для работы манипулятора при параллельном включении цилиндров, например Ц1 и Ц3, ведущие звенья 1 и 2 поворачиваются на заданный угол, при этом ведомые звенья 9 и 10, поворачиваясь в противоположном направлении, перемещают прямолинейно промежуточное звено 11 со схватами 12. Приводы ведущих звеньев идентичны.

Рассмотрим фрагмент пневматической схемы привода (рис. 6.2). Пневмопривод состоит из двух цилиндров Ц1 и Ц2, шток-рейки которых кинематически связаны через шестерню, посаженную на ведущий вал звена манипулятора. Управление цилиндрами осуществляется от распределителей Р1 и Р2. Распределитель Р3 соединен с магистральной и выхлопной линиями. Редукционный клапан РК предназначен для регулирования величины противодавления.

Обратный клапан ОК обеспечивает разъединение напорной и выхлопной пневмолиний и сброс воздуха через предохранительный клапан ПК в атмосферу при превышении давления в тормозной полости выше установленного. Управление распределителями осуществляется от системы управления (не показана) по сигналам, поступающим от датчиков положений ВК1 и ВК3, и датчика переключения режима работы привода ВК2.

Пневмопривод работает следующим образом.

В начальный момент времени в полости цилиндра Ц1 давление p_ap, установленное при помощи редукционного клапана РК, обеспечивает выборку зазоров в паре шток-рейка и шестерня при позиционировании выходного звена. В полости цилиндра Ц2 давление равно магистральному давлению p_м. По сигналу системы управления распределитель Р1 включается, соединяя полость цилиндра Ц1 с магистралью. Распределители Р2 и Р3 отключены и соединяют, соответственно, полость цилиндра Ц2 с выхлопной линией, и выхлопную линию с атмосферой с давлением p_a. Происходит перемещение шток-рейки цилиндров из положения, определяемого датчиком ВК3, в положение, определяемое датчиком ВК1. Привод работает в режиме разгона выходного звена. При прохождении датчика ВК2 по команде от системы управления срабатывает распределитель Р3, соединяя выхлопную магистраль через редукционный клапан РК с напорной магистралью, обеспечивая тем самым торможение выходного звена противодавлением.

Для анализа выбранных на этапе проектировочного расчета конструктивных параметров привода строят полную математическую модель манипулятора, учитывающую как уравнения движения манипулятора, так и уравнения изменения давлений в полостях цилиндров.


Х₁


S

p_a

0

Ц1

F,

Х₀

Х₂

Ц1

Р₂, Т₂

P₃

1

p_a

p_пд

p_м

P₁

1

0

f_a

P₂

1

0


Рис. 6.2. Фрагмент пневматической принципиальной схемы манипулятора
При построении полной математической модели манипулятора необходимо получить уравнение движения манипулятора и законы изменения давлений в полостях цилиндров.

Для вывода уравнений, описывающих процессы, протекающие в полостях цилиндров, исследуем термодинамику этих процессов. Индекс 1 будет относиться к рабочей камере цилиндра, индекс 2 к выхлопной камере цилиндра.

При выполнении расчета принимаем во внимание следующие допуски:

– процессы, протекающие в приводе, считаем квазистационарными, т. е. переменные параметры газа во времени изменяются одновременно по всему объему, так как возмущения в воздушной среде распространяются со скоростью звука, намного превосходящую скорость деформации объема;

– воздух рассматриваем как идеальный газ, в котором силы внутреннего трения равны нулю.

Цикл работы привода разбиваем на два этапа.

На первом этапе происходит разгон выходного звена привода до максимальной скорости _max. Процессы, протекающие при этом в полостях цилиндров, соответствуют режимам наполнения полости переменного объема и, соответственно, истечения из полости переменного объема при начальном перепаде давлений.

На втором этапе происходит торможение выходного звена, при этом в рабочей полости соответствующего цилиндра продолжается процесс наполнения полости переменного объема, а в выхлопной полости цилиндра возможна реализация следующих процессов:

– сжатие воздуха в полости переменного объема без его истечения в атмосферу от начального давления p_2,0 = p_a + p₂, где p₂ – потери давления в выхлопной магистрали, при этом распределитель Р2 переключается в положение 1;

– сжатие воздуха в полости переменного объема без его истечения в атмосферу от начального давления p_2,0 = p_ap + p₂, при этом распределитель Р2 переключается в положение 0, а распределитель Р3 в положение 1;

– истечение воздуха из полости переменного объема при достижении давления p_pk настройки предохранительного клапана ПК.

Запишем закон сохранения энергии для пневмопривода:
(6.1)
где – количество тепловой энергии, поступившей в полость цилиндра Ц1; – работа, совершаемая на поршне цилиндра; – скорость теплообмена с окружающей средой; – изменение внутренней энергии системы; m₁ – масса воздуха, поступившего в полость цилиндра Ц1; T₁ – температура поступившего воздуха; V₁ – объем полости цилиндра Ц1; c_p – теплоемкость воздуха при постоянном давлении р; c_V– теплоемкость воздуха при постоянном объеме V; ρ₁ – плотность поступившего воздуха.

Подставляя в формулу (6.1) уравнение плотности , вычисляем состояние идеального газа и, обозначив массовый расход воздуха , получим
, (6.2)
где – показатель адиабаты; Дж/(кг · К) – газовая постоянная для воздуха.

Теплообмен с окружающей средой из-за высокой скорости протекающих процессов не учитываем, т. е. считаем процесс адиабатическим, а членом можно пренебречь, при этом T₁ = T_м, где T_м – температура воздуха в магистральном трубопроводе.

В этом случае уравнение (6.2) для полости цилиндра Ц1 примет вид
. (6.3)
Для полости цилиндра Ц2 уравнение сохранения энергии запишется в виде
. (6.4)
Учитывая, что выполним необходимые преобразования:



получим уравнение, описывающее процесс заполнения полости переменного объема:
(6.5)

При истечении воздуха из полости цилиндра Ц2 уравнение сохранения энергии запишется аналогично и, выполнив необходимые преобразования, получим уравнение, описывающее процесс истечения воздуха из полости переменного объема:
(6.6)
где i = 1, 2 – индексы полостей цилиндров.

Приведем уравнение (6.5) к виду, удобному для интегрирования:
, (6.7)
где х₀ – начальное положение поршня; – линейная скорость поршня; коэффициенты , при температуре воздуха в магистрали Т_м = 293 K; .

Приведем к виду, удобному для интегрирования, уравнение (6.6):
(6.8)
где s – ход поршня.

Для малых промежутков времени и участков интегрирования перепишем уравнения (6.7) и (6.8). В итоге получим систему уравнений в приращениях, описывающих процессы изменения давлений в рабочей и выхлопной камерах привода:
(6.9)
При торможении выходного звена привода противодавлением р_ар без истечения воздуха из выхлопной полости необходимо определить максимально возможное давление р_max2 сжатия в камере цилиндра и задать длину участка торможения s_t.

При адиабатическом сжатии процессы, происходящие в выхлопной камере двигателя, описываются уравнением
(6.10)

где m – допустимая степень сжатия, а противодавление р_ар может изменяться в пределах

Обозначив через х_t перемещение поршня при торможении,
т. е. 0 < x_t < s_t, перепишем выражение (6.10) в виде
(6.11)
где p_тк – давление в тормозной камере.

Получили характеристику процесса торможения без истечения воздуха из полости цилиндра. Очевидно, что чем меньше х₀, т. е. мертвый объем камеры, тем жестче характеристика, и наоборот, причем сила сопротивления (противодавления) зависит только от координаты х_t, т. е. является упругой силой, отсюда и термин «пневмопружина».

Определим максимальную степень сжатия для пневмопружины.

Максимальное давление в камере назначается исходя из максимальной температуры T_max, которая допускается без опасности чрезмерного перегрева или вспышки смазочных масел, распыленных маслораспылителем блока подготовки воздуха. Принимая в качестве верхнего предела температуру вспышки минерального масла T_max = 160…180 С можем переписать уравнение теплоизолированного потока (6.10) в виде
.
Принимая T_max= 473 К, Т₀ = 293 К, получим m  3,9.

Реально, из-за рассеяния тепла предел несколько выше.

В практических расчетах при назначении степени сжатия учитывается также частота повторяемости процесса. При частой повторяемости m = 2…4, при редкой m = 6…7.

Раскладывая правую часть уравнения (6.10) в ряд Тейлора и выполнив необходимые преобразования, сможем определить необходимую длину участка торможения:
(6.12)
Для определения динамических характеристик привода систему (6.9) необходимо решить совместно с уравнением движения привода.

Уравнение движения получено с использованием уравнений Лагранжа второго рода и для исследуемого манипулятора при отработке прямолинейного перемещения схвата при жесткой кинематической связи между звеньями оно имеет вид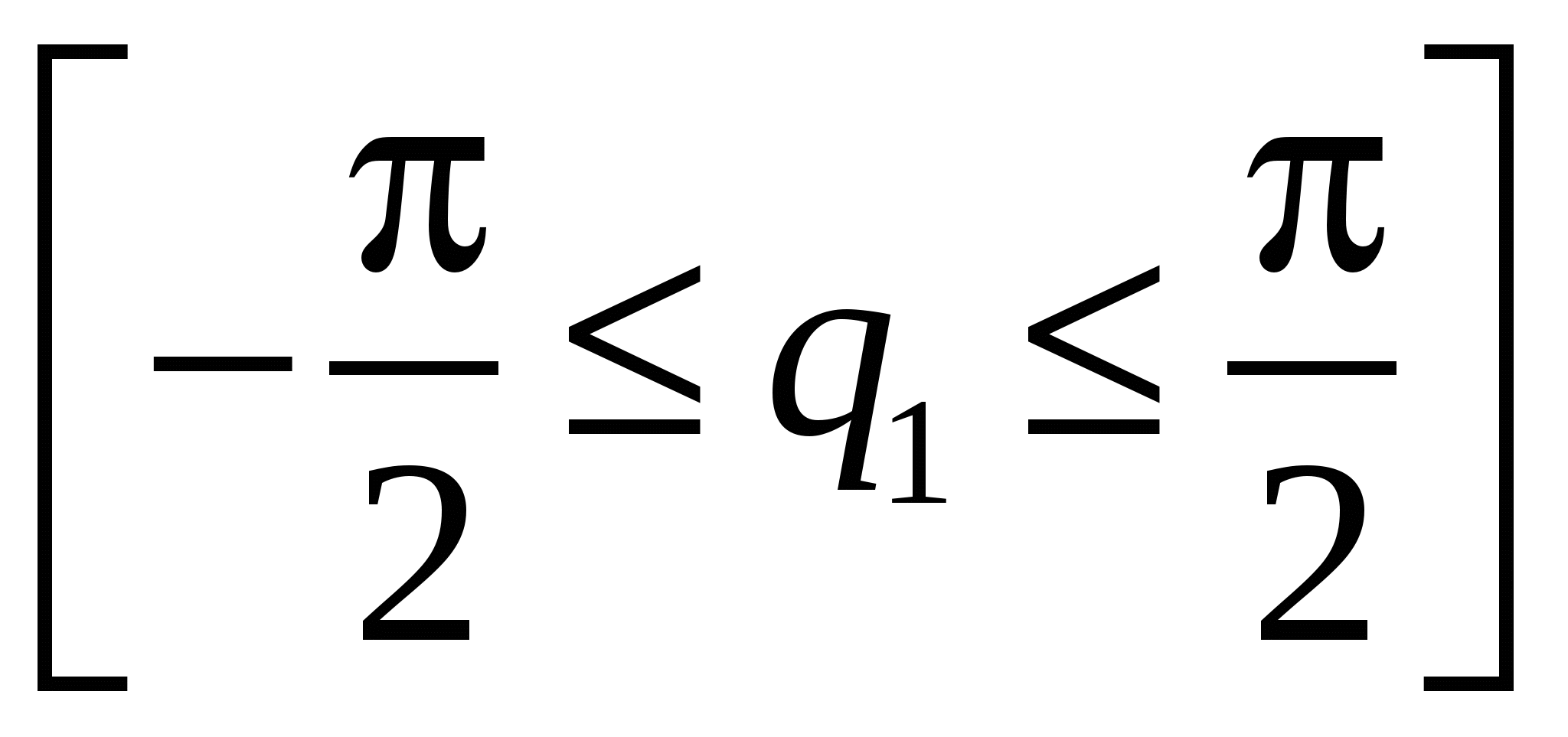

(6.13)
где – угловое ускорение выходного звена привода (ведущего звена манипулятора); – угловая скорость ведущего звена; – текущее значение угла поворота ведущего звена ;

здесь
,
где – масса звена манипулятора; l – длина звена манипулятора; – момент сил, приложенный к ведущим звеньям.

В исследуемом манипуляторе использованы параллельные приводы звеньев, т. е. , где момент , развиваемый каждым приводом:
(6.14)
где r– радиус шестерни ведущего звена, сопряженной со шток-рейкой; – усилие, развиваемое приводом.

Скорости поршней цилиндров связаны с угловой скоростью ведущих звеньев соотношением , линейная скорость перемещения схватов определяется по выражению
. (6.15)
Усилие, развиваемое приводом
(6.16)
где – силы трения; – силы инерции поступательно перемещающихся деталей привода.

Массой поступательно перемещающихся деталей привода, по сравнению с массой подвижных деталей и узлов манипулятора, пренебрегаем.

Силы трения считаем постоянными и определяем по формуле
(6.17)
где b – ширина уплотнения; D – диаметр цилиндра; n – число уплотнений; p_к = 0,7 МПа – принятое радиальное контактное давление уплотняющих элементов; f_тр = 0,15 – коэффициент трения скольжения.

Система уравнений (6.9), (6.13)–(6.17) полностью описывает поведение манипулятора и процессы, протекающие в камерах приводов.