Методические указания к виртуальному лабораторному практикуму Вологда 2007
 Скачать 1.84 Mb. Скачать 1.84 Mb.
|
Лабораторная работа № 1.2 |
| Номер опыта | D, мм | t, с | , Пас | , Пас | ()2, (Пас)2 |
| 1 | D1 = D2 = D3 = | | | | |
| D = | |||||
| 2 … | D1 = … | … | … | … | … |
| 5 | D1 = D2 = D3 = | | | | |
| D = | |||||
| | | | | | |
4. Приготовьте к работе секундомер. Аккуратно опустите шарик в сосуд с глицерином; в момент прохождения им верхней метки включите секундомер, в момент прохождения нижней метки – выключите. Время движения между метками t занесите в третий столбец таблицы.
5. Повторите пп. 3 и 4 еще четыре раза с новыми шариками.
6. Для каждого из пяти опытов вычислите по формуле (13) коэффициент вязкости , используя при расчетах среднее из трех значение диаметра шарика D, выраженное в метрах. Результаты запишите в следующий столбец таблицы.
7. Найдите среднее значение коэффициента вязкости
8*. Определите абсолютные приборные ошибки прямых измерений расстояния между метками l, диаметра шарика D и времени его падения t, а также относительные ошибки El , ED и Et .
9*. Найдите абсолютную приборную погрешность косвенного измерения коэффициента вязкости . Для этого, если потребуется, используйте формулу
10. Оцените полную абсолютную и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения коэффициента вязкости. Сравните полученное значение с табличным (см. справочные материалы).
Контрольные вопросы:
Каков физический смысл коэффициента вязкости жидкости? От чего он зависит?
Объясните механизм внутреннего трения для жидкостей и газов.
Распишите силы, действующие на тело (в частности шарик), падающий в жидкости.
Объясните причины, приводящие к равномерному (установившемуся) падению шарика в жидкости.
Оцените время падения шарика в жидкости из состояния покоя до приобретения скорости установившегося движения, какой путь при этом будет пройден?
Получите формулу (12) для коэффициента вязкости жидкости.
Как зависит скорость падения шарика в жидкости от его диаметра?
Приведите примеры других методов измерения вязкости жидкости, изложите их суть.
Литература:
[3]- §14, 53, 58-60; [13]-п.п.: 1.9, 1.42, 1.43.
Лабораторная работа № 1.3
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
НА МАЯТНИКЕ ОБЕРБЕКА
Цель работы:1) изучение кинематических и динамических характеристик вращательного движения;
2) экспериментальное определение момента инерции крестовины маятника Обербека и момента сил трения;
3) проверка справедливости закона сохранения (превращения) энергии механической системы.
Схема экспериментальной установки
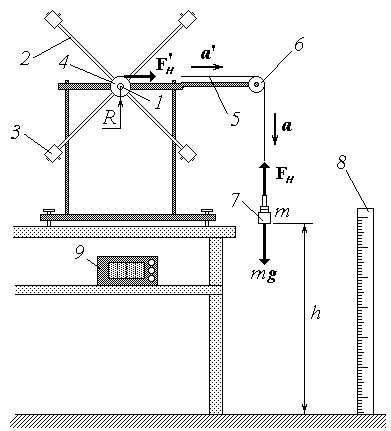
1 – ось вращения;
2 – стержень;
3 – груз-насадка;
4 – шкив;
5 – нить;
6 – блок;
7 – груз;
8 – линейка;
9 – секундомер
Рис. 1
Описание установки
Основным элементом маятника Обербека (рис. 1) является крестовина, способная свободно вращаться вокруг неподвижной горизонтальной оси 1. Крестовина состоит из четырех стержней 2 с грузами-насадками 3, расположенными симметрично относительно оси вращения. С крестовиной жестко скреплен шкив 4 радиусом R. На шкив намотана нить 5, перекинутая через легкий блок 6. К свободному концу нити привязан груз 7, массу которого m можно изменять в процессе опытов. Для измерения высоты h расположения груза над полом служит линейка 8, а для измерения времени его падения – секундомер 9.
Теория метода
Если поднятый на высоту h груз отпустить, то он начнет падать с ускорением
в проекциях на направление движения груза имеет вид:
ma = mg – Fн,
откуда:
Fн = т(g – a). (1)
Пренебрегая массами нити 5 и блока 6, можно считать, что нить действует на поверхность шкива касательной силой
Мн = т(g – a)R . (2)
Под действием момента
J = Мн – Мтр , (3)
где J– момент инерции крестовины маятника Обербека относительно оси вращения.
Известно, что момент инерции зависит только от распределения массы тела относительно оси. Для крестовины маятника величина J определяется в основном положением грузов-насадок 3 на стержнях 2. Если их положение в ходе опытов не изменяется, то и момент инерции остается постоянным. Момент сил трения также можно считать практически неизменным. Поэтому зависимость углового ускорения от момента силы натяжения Мн , согласно уравнению (3), имеет линейный характер. Определив опытным путем значения при различных Мн и обработав соответствующим образом полученную экспериментальную зависимость (Мн), с помощью этого уравнения можно найти неизвестные величины J и Мтр . Рассмотрим теперь методику измерения углового ускорения и момента силы натяжения Мн .
Так как нить 5 практически нерастяжима, все ее точки, включая точки на поверхности шкива, движутся с одинаковым ускорением
Измерив высоту h и время падения груза t, можем найти ускорение
Если известны масса груза т и радиус шкива R, то по формуле (2) можно рассчитать момент силы натяжения нити Мн .
Угловое ускорение вращения шкива, а следовательно, и крестовины и тангенциальное (касательное) ускорение точек на поверхности шкива связаны известным соотношением
Таким образом, зная массу груза т, радиус шкива R и высоту h, с которой падает груз, а также измерив время его падения t, можно экспериментально определить величины и Мн .
Рассмотрим теперь превращение энергии в вышеописанном опыте. Поднятый на высоту h груз обладает потенциальной энергией
Wp = mgh; (6)
кинетическая энергия системы «груз + крестовина» при этом равна нулю. В момент падения груза на пол его потенциальная энергия обращается в ноль, но за счет ее уменьшения груз приобретает кинетическую энергию
а крестовина – кинетическую энергию вращения
где v – скорость груза в момент падения; – угловая скорость вращения крестовины к этому моменту.
Итак, начальное значение полной механической энергии рассматриваемой системы равно W0= Wp , а конечное W = Wk1 + Wk2 . Изменение энергии:
Как известно, изменение полной механической энергии консервативной системы равно нулю, а при наличии неконсервативных сил – их работе. В данной системе действуют неконсервативные силы трения, работа которых равна
Атр = – Мтр, (9)
где – угол поворота крестовины за время падения груза. Знак « – » отражает тот факт, что работа сил трения и сопротивления всегда отрицательна (угол между направлениями силы и перемещения равен 180). Итак, закон сохранения (превращения) энергии в данном случае можно записать как
или
С учетом соотношений (6)-(9) уравнение (10) примет вид:
Для экспериментальной проверки справедливости уравнения (11) необходимо знать все входящие в него величины. К ним относятся, во-первых, заранее известные ускорение свободного падения g, масса груза т и высота h; во-вторых, определяемые путем обработки экспериментальной зависимости момент инерции крестовины J и момент сил трения Мтр ; в-третьих, кинематические характеристики системы v, и . Остановимся на определении последних.
Скорость груза в момент его падения на пол найдем исходя из закономерностей равноускоренного движения:
Такую же по величине скорость имеют и точки на поверхности шкива. Используя связь между линейной и угловой скоростями, получим
Так как линейное расстояние, пройденное точками на поверхности шкива, равно перемещению груза за тот же промежуток времени, угол (в радианах) может быть рассчитан как
Порядок измерений и обработки результатов
1. Запишите радиус шкива R , выразив его в метрах, в тетрадь (R=17мм).
2. Занесите во второй столбец таблицы 1 значение массы груза т (в кг).
Таблица 1.
| Номер опыта | т, кг | t, c | а, м/с2 | Мн , Нм | , с – 2 | Мн2, (Нм)2 | Мн, Нм/с2 |
| 1 | | t1 = t2 = t3 = | | | | | |
| t = | |||||||
| 2 … | … | t1 = … | … | … | … | … | … |
| 6 | | t1 = t2 = t3 = | | | | | |
| t = | |||||||
| | | | = | | | | |
3. Вращая крестовину, намотайте нить на шкив так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом, запишите значение высоты в тетрадь (значение hзадает преподаватель или спишите с экрана монитора).
4. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы 1.
5. Повторите пп. 3 и 4 с тем же грузом еще два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t.
6. Увеличивая массу груза согласно рекомендациям, выполните пп. 2-5 еще пять раз.
7. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (4), подставляя в нее среднее из трех измеренных значений времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в четвертый столбец таблицы 1.
8. По формулам (2) и (5) вычислите значения момента силы натяжения нити Мн и углового ускорения . Результаты занесите в соответствующие столбцы табл. 1.
9. Руководствуясь правилами [1], постройте график зависимости углового ускорения от момента силы натяжения (в данной работе необходимо, чтобы начало координат совпадало с нулевыми значениями откладываемых величин и Мн). Нанесите на график экспериментально полученные точки.
10. Одним из описанных ниже способов* обработайте линейную экспериментальную зависимость (Мн) и найдите значения момента инерции крестовины J и момента сил трения Мтр. Запишите эти значения в тетрадь.
11. Для одного из проделанных опытов рассчитайте по формулам (12)-(14) скорость груза v, угловую скорость вращения и угол поворота крестовины маятника Обербека в момент падения груза на пол.
12. Вычислите значения левой и правой частей уравнения закона сохранения энергии (11). Сравнив эти значения между собой, сделайте выводы.
Обработка зависимости (Мн)
Угловое ускорение крестовины и момент силы натяжения нитиМн связаны уравнением основного закона динамики вращательного движения (3). Зависимость (Мн) можно представить в виде
где
Обработку экспериментальной зависимости (Мн) можно провести либо графически, либо методом наименьших квадратов.
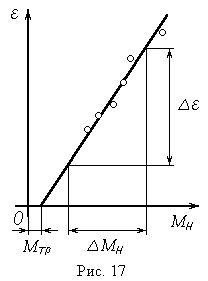 Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (рис. 2).
Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (рис. 2). В
Рис. 2
еличина K в уравнении (15) представляет собой угловой коэффициент прямой, т.е. тангенс угла ее наклона к оси абсцисс. Согласно (16), момент инерции J есть величина, обратная K, – значит, его можно найти как котангенс этого угла. Выбрав на сглаживающей прямой две достаточно удаленные друг от друга точки, рассчитайте значение J как отношение отрезков
причем величины отрезков Мн и должны быть взяты с учетом масштаба графика и выражены в соответствующих единицах измерения: Мн – в Нм, а – в рад/с2 или в с – 2. Только в этом случае результат будет правильным, и момент инерции будет иметь размерность кгм2.
Метод наименьших квадратов. (Подробно этот метод рассмотрен в [1]). Изучив данный материал, заполните два последних столбца табл. 1. Найдите суммы значений величин в последних четырех столбцах и занесите их в строку « = ». Вычислите коэффициенты Kиb зависимости (15); результаты расчетов запишите в тетрадь. Для определения момента инерции крестовины J и момента сил трения Мтр воспользуйтесь соотношениями (16). На графике зависимости (Мн) проведите прямую по двум точкам, координаты которых рассчитайте по найденным значениям коэффициентов. Убедитесь в правильности проведенных расчетов (прямая должна «наилучшим» образом пройти через экспериментальные точки).
Контрольные вопросы
Какие величины характеризуют вращательное движение?
Что характеризует момент инерции твердого тела относительно оси вращения? Как он рассчитывается?
Сформулируйте и докажите теорему Штейнера.
Как изменится кинетика опускания гири, если грузы на крестовине передвинуть ближе (дальше) к оси вращения.
Дайте определение момента силы. Какие моменты сил действуют на крестовину маятника Обербека в этой работе.
Запишите математически и сформулируйте главный закон динамики вращательного движения.
Покажите, что в пренебрежении трением, расчетная формула для момента инерции маятника Обербека будет иметь вид:
Запишите и поясните закон сохранения (превращения) механической энергии в этой работе.
Литература:
[3]- §36-41; [6]- §5.4; [13]-п.п.: 1.31-1.34.

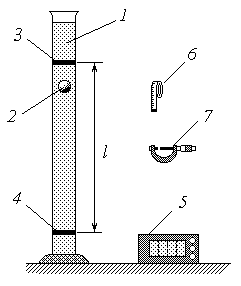 хема экспериментальной установки
хема экспериментальной установки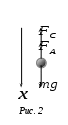 Рассмотрим движение тяжелого шарика в вязкой жидкости. Будем считать, что плотность материала шарика ш больше плотности жидкости ж. Очевидно, что в этом случае шарик начнет тонуть. Характер его движения определяется тремя действующими на него силами (рис. 2): силой тяжести
Рассмотрим движение тяжелого шарика в вязкой жидкости. Будем считать, что плотность материала шарика ш больше плотности жидкости ж. Очевидно, что в этом случае шарик начнет тонуть. Характер его движения определяется тремя действующими на него силами (рис. 2): силой тяжести