Лабораторная работа № 2.1
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА
Цель работы:1)изучение явления внутреннего трения в газах;
2) экспериментальное определение коэффициента вязкости воздуха;
3) оценка средней длины свободного пробега молекул и их эффективного диаметра.
С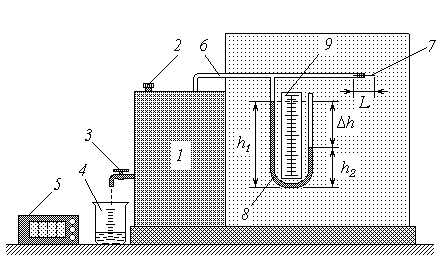 хема экспериментальной установки хема экспериментальной установки
1 – резервуар;
2 – крышка;
3 – кран;
4 – мерный стакан;
5 – секундомер;
6 – трубка;
7 – капилляр;
8 – манометр;
9 – линейка
Рис. 1
Теория метода
Для определения коэффициента вязкости воздуха в лабораторной работе (рис. 1) используется экспериментальная установка, основные элементы которой выполняют следующие функции.
В резервуар 1 заливается вода, после чего он герметично закрывается завинчивающейся крышкой 2. Для слива воды предназначен кран 3; мерный стакан 4 позволяет контролировать объем сливаемой воды V, а секундомер 5 – время ее истечения t. Воздух в надводной части резервуара сообщается с атмосферой через трубку 6, в свободный конец которой вмонтирован капилляр (очень узкая стеклянная трубка) 7 длиной L. По мере вытекания воды из резервуара его надводный объем увеличивается, что приводит к падению в нем давления воздуха. При возникновении на концах капилляра перепада давлений р начинается всасывание воздуха. Для измерения перепада давлений р используется манометр 8, представляющий собой U-образную стеклянную трубку с подкрашенной водой. Одно колено манометра сообщается через трубку 6 с воздухом в резервуаре, а другое (открытое) – с атмосферой. Уровни воды в коленах манометра h1 и h2 измеряются с помощью линейки 9.
При понижении давления в резервуаре уровень воды в левом (на схеме) колене повышается, а в правом – понижается, пока давление столба воды h = h1 – h2 не уравновесит перепад давлений р:
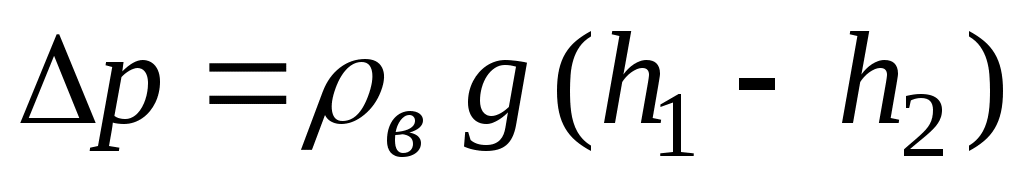 , (1) , (1)
где в – плотность воды; g – ускорение свободного падения.
В установившемся режиме объемный расход воздуха G (объем, протекающий за единицу времени) через капилляр равен объемному расходу вытекающей из резервуара воды:
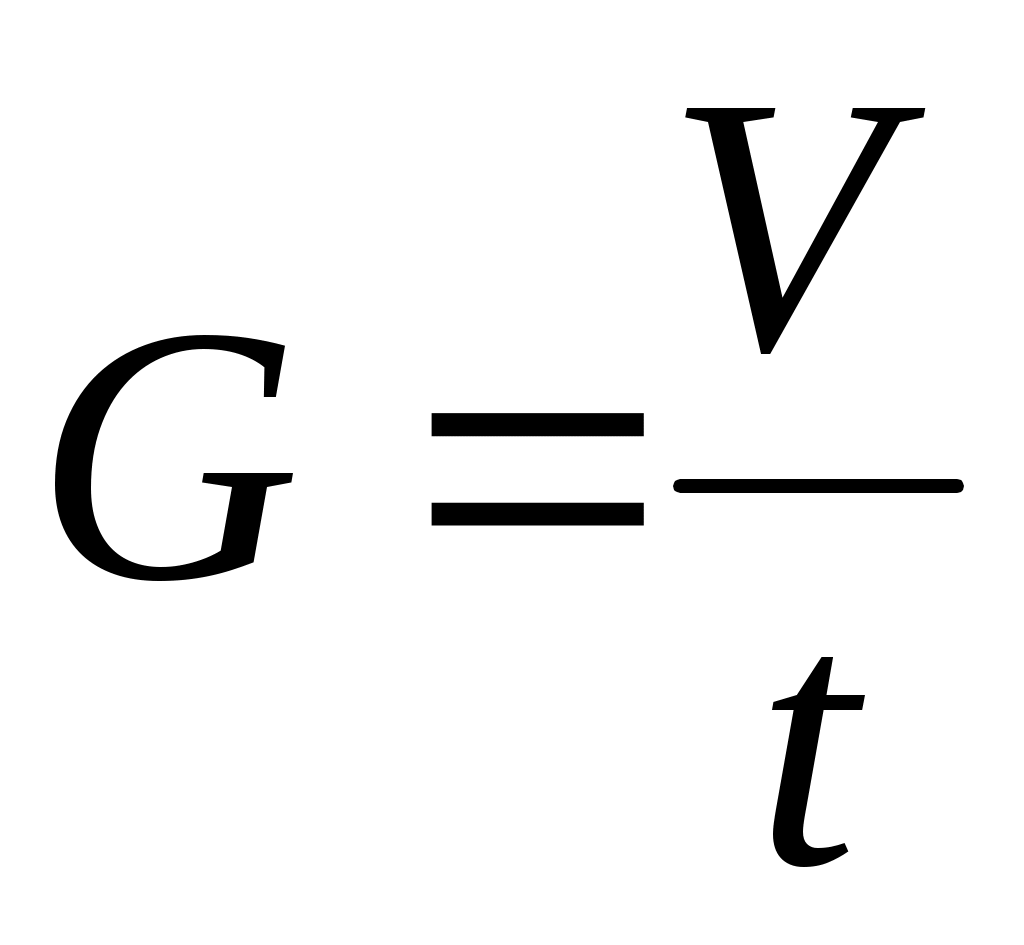 . (2) . (2)
Очевидно, что величина G тем больше, чем больше перепад давлений р и внутренний радиус капилляра r, и тем меньше, чем длиннее капилляр и больше вязкость текущего воздуха . Количественно взаимосвязь этих величин определяется формулой Пуазейля:
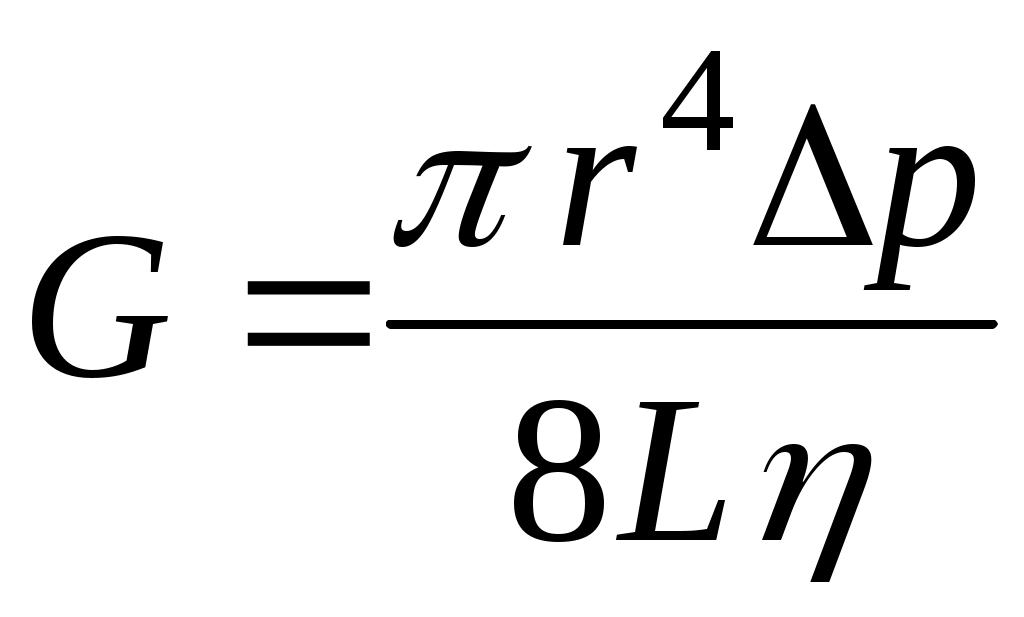 . .
С учетом соотношений (1) и (2) эта формула примет вид:
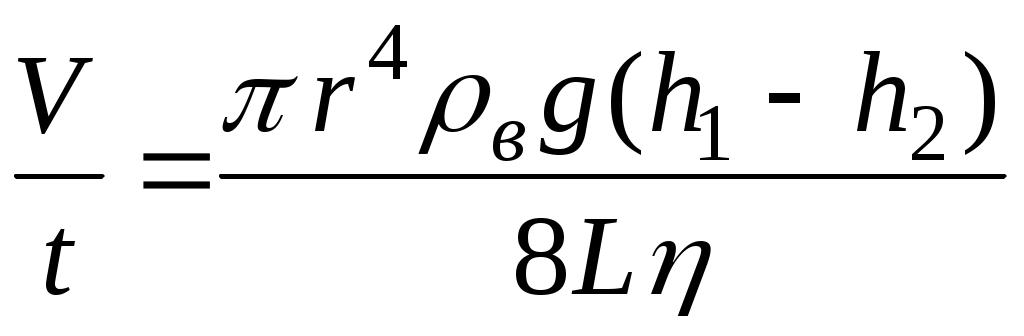 . (3) . (3)
Зная геометрические размеры (длину L и радиус r) капилляра и измеряя величины V, t, h1 и h2 , с помощью формулы (3) можно найти коэффициент вязкости воздуха:
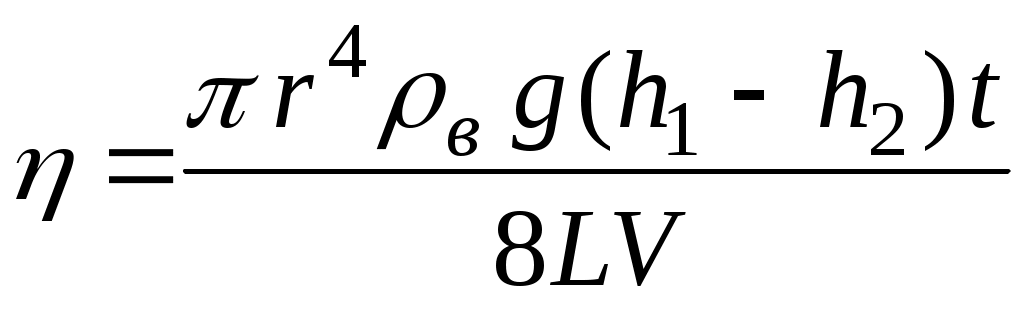 . .
Значения L,r,g и в представляют собой константы; если в процессе опытов поддерживать неизменным освобождаемый объем V, то расчетную формулу для коэффициента вязкости можно представить в виде:
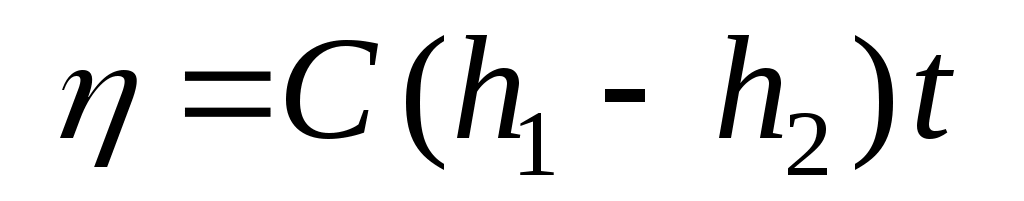 , (4) , (4)
где
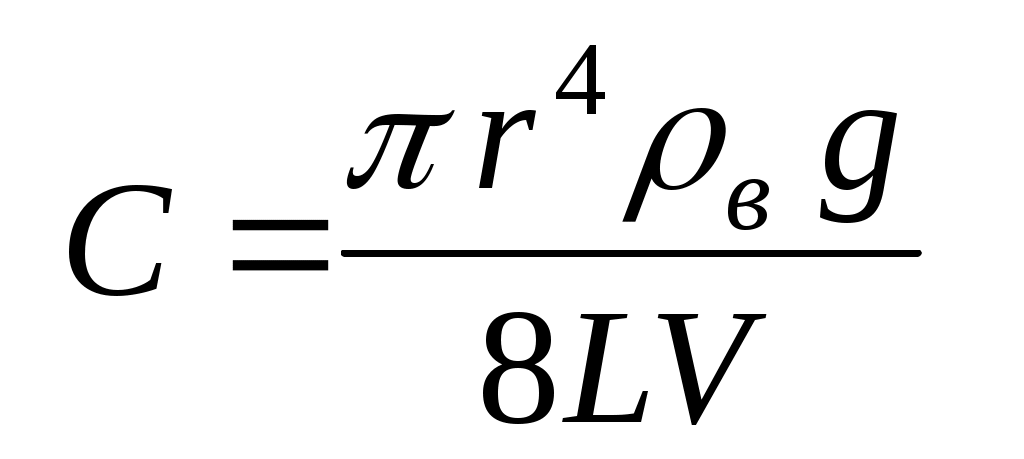 . (5) . (5)
Молекулярно-кинетическая теория дает следующее выражение для коэффициента вязкости идеального газа:
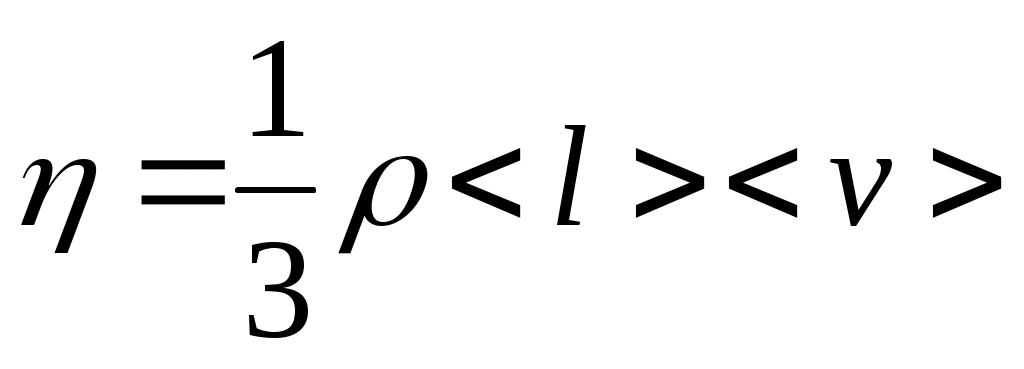 , (6) , (6)
где – плотность газа; < l> – средняя длина свободного пробега молекул; <v> – средняя скорость их хаотического (теплового) движения. Из выражения (6) можно найти среднюю длину пробега:
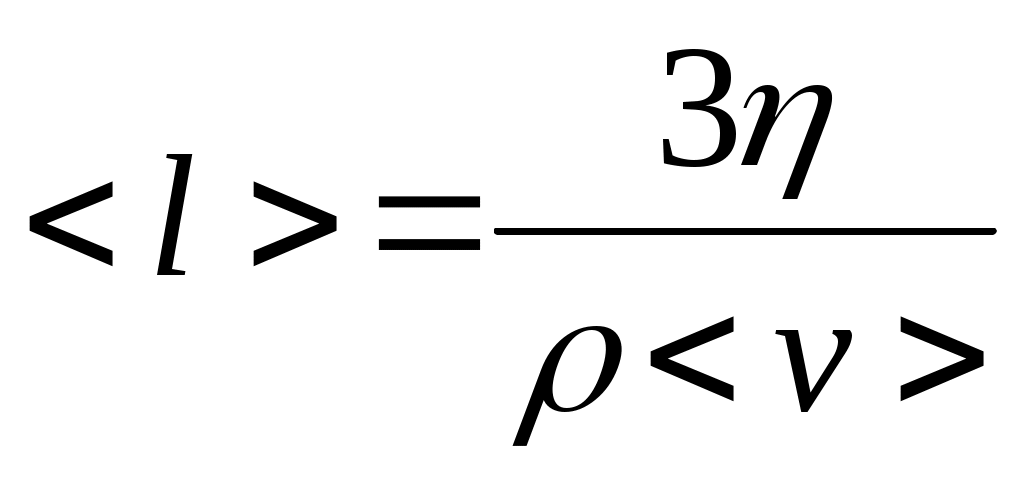 . (7) . (7)
Плотность газа выразим из уравнения Менделеева-Клапейрона:
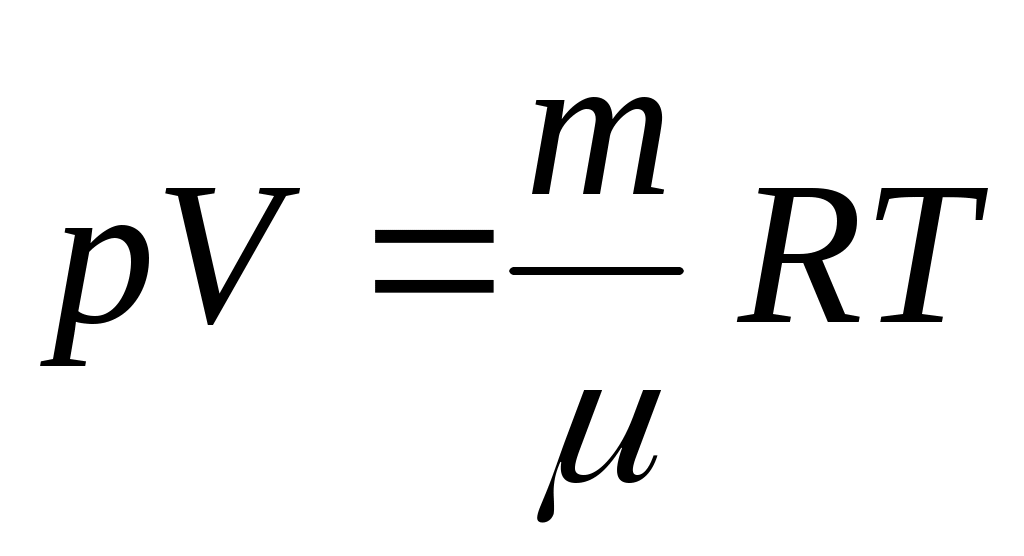 , ,
откуда
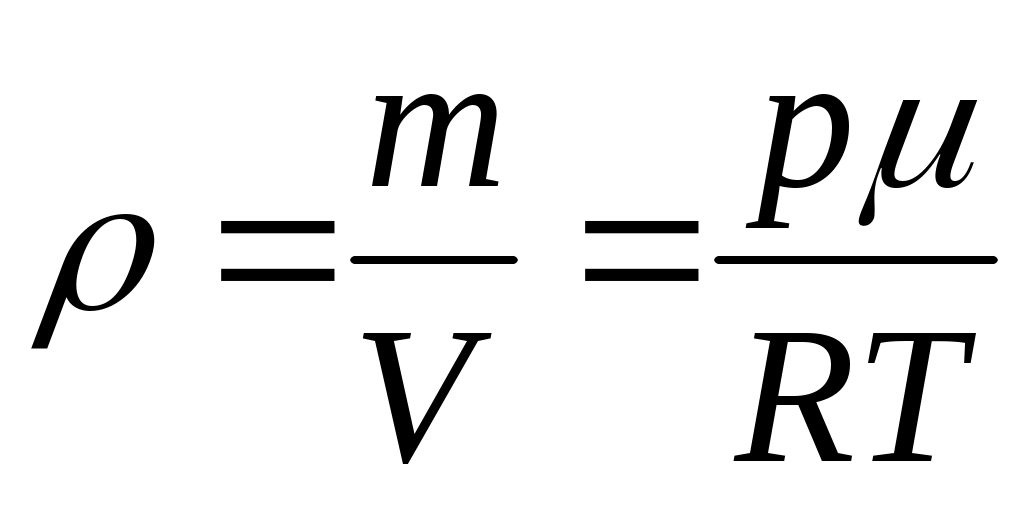 , (8) , (8)
где р – давление; V – объем; т – масса газа; – молярная масса; R –универсальная газовая постоянная; Т – абсолютная температура.
Распределение молекул идеального газа по скоростям (распределение Максвелла) позволяет найти среднюю скорость их теплового движения как
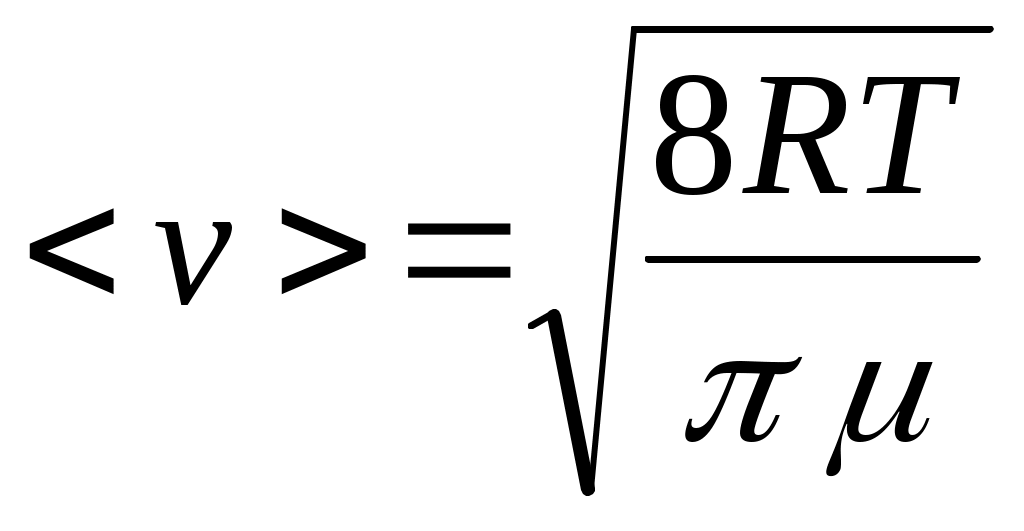 . (9) . (9)
Подставляя выражения (8) и (9) в (7), получим
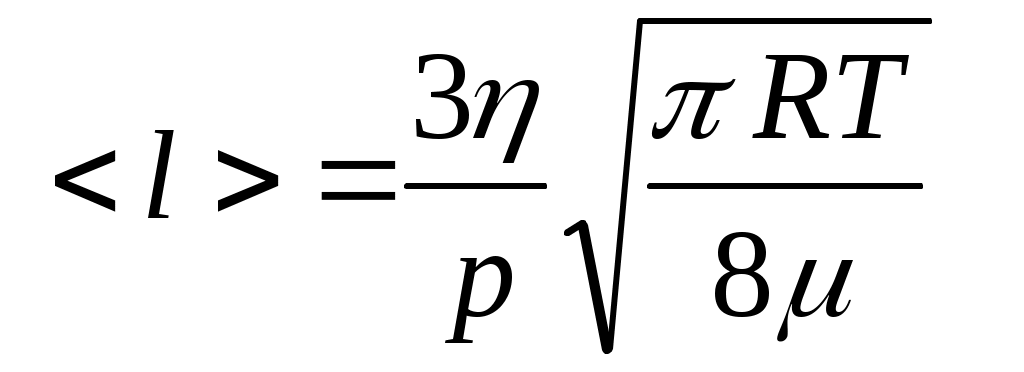 . (10) . (10)
В соответствии с теорией, средняя длина свободного пробега < l > молекул идеального газа обратно пропорциональна их концентрации п и эффективному сечению , т.е. квадрату эффективного диаметра dэ :
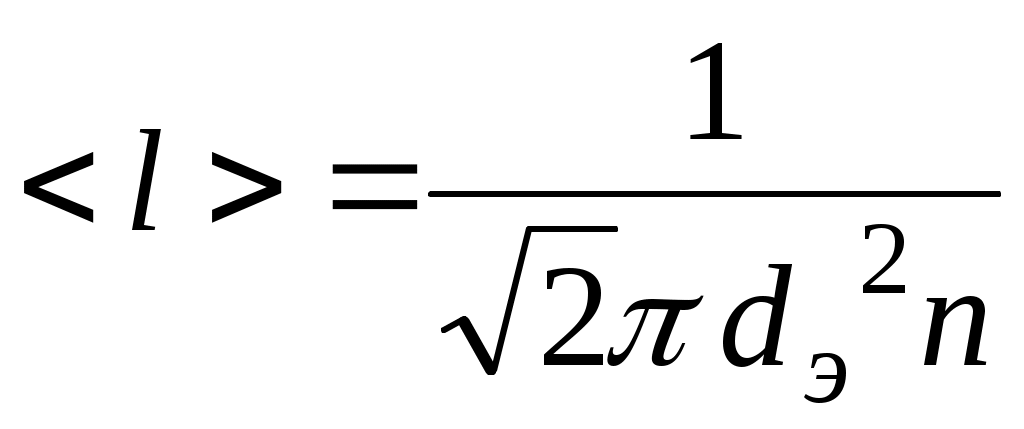 , ,
откуда
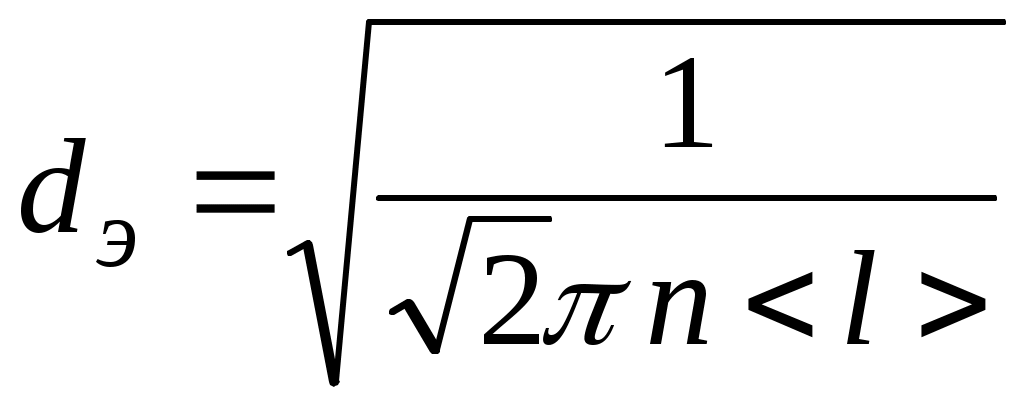 . .
Учитывая известное соотношение
p = nkT,
где k – постоянная Больцмана, выразим концентрацию молекул через давление газа и его температуру:
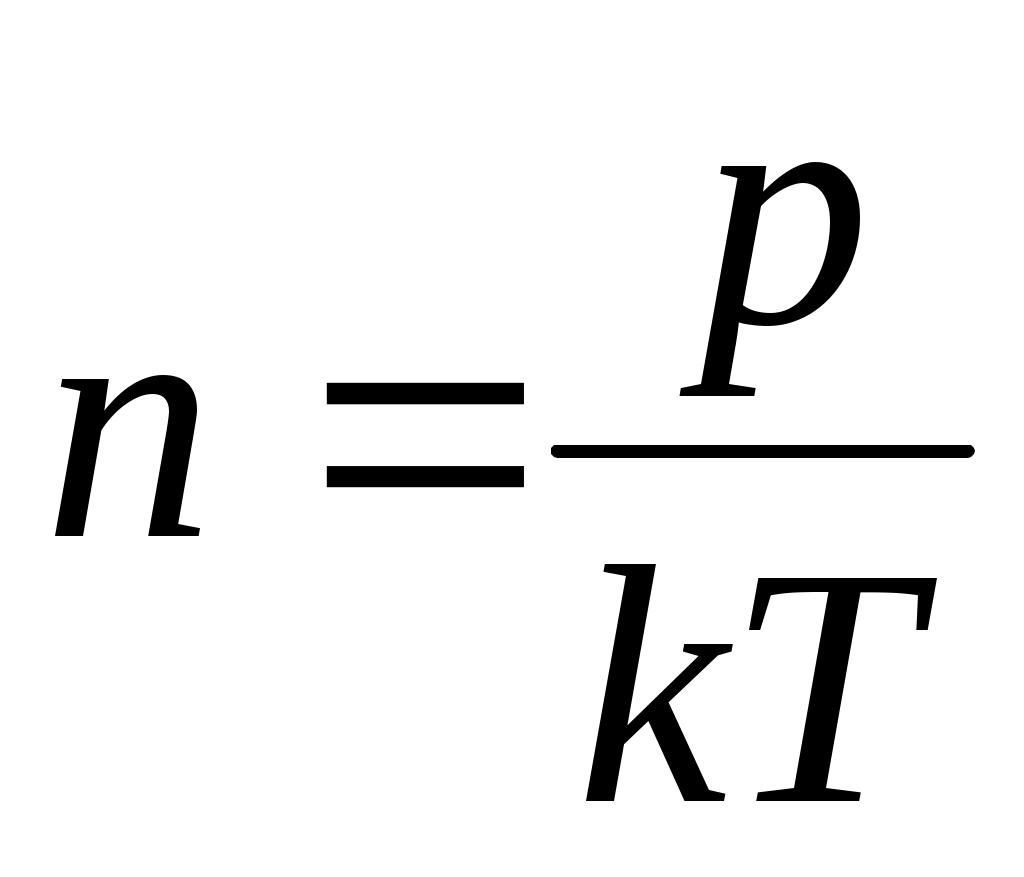 ; ;
тогда
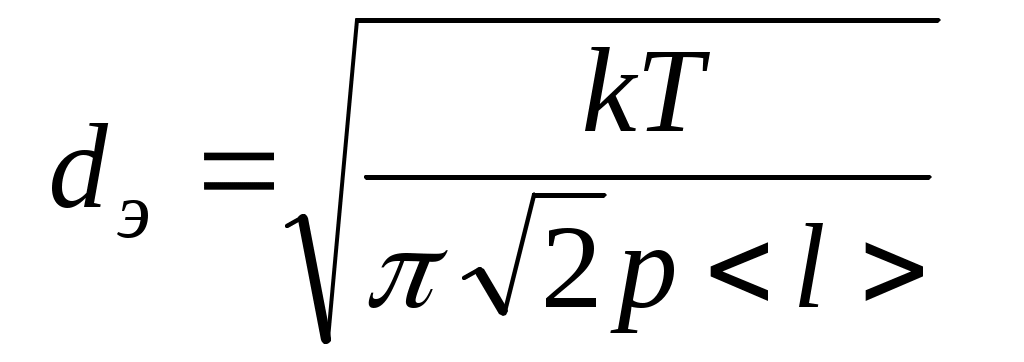 . (11) . (11)
Порядок измерений и обработки результатов
1. Выпишите в тетрадь геометрические размеры капилляра L и r (спишите с экрана монитора), выразив их в метрах. Используя справочные материалы, спишите значения известных констант g, R, k, а также плотность воды в . Молярную массу воздуха примите равной = 0,029 кг/моль. Запишите рекомендуемое значение объема выливаемой из резервуара воды V (на мониторе).
2. Рассчитайте по формуле (5) и запишите в тетрадь значение константы С (в Н/м3).
3. Спишите с экрана монитора данные о параметрах окружающего воздуха.
4. Температуру воздуха Т переведите из градусов Цельсия в кельвины, а давление р – из миллиметров ртутного столба в паскали.
5. Подставьте под кран сливную емкость; откройте кран и следите за уровнями воды в манометре. После установления постоянных уровней подставьте под кран мерный стакан и одновременно включите секундомер. С помощью линейки определите и запишите в таблицу высоту уровней h1 и h2 , выразив эти значения в метрах. В момент наполнения стакана до заданного объема V выключите секундомер и закройте кран. Занесите в таблицу показания секундомера t.
Номер опыта
|
h1 ,
м
|
h2 ,
м
|
t,
c
|
,
мкПас
|
, мкПас
|
()2, (мкПас)2
|
1
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
5
|
|
|
|
|
|
|
|
|
|
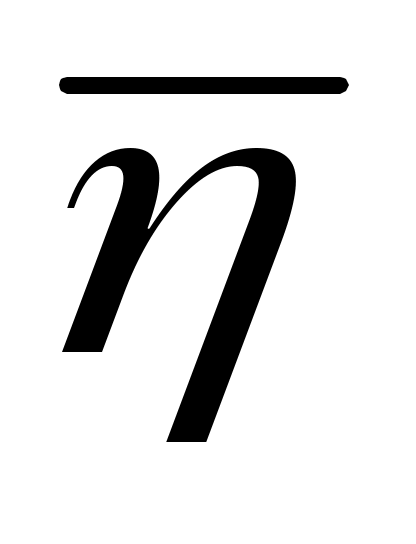 = =
|
|
=
|
|
5. Повторите описанный в п. 5 опыт еще четыре раза, стараясь устанавливать различный расход воды из крана (а значит, различный перепад уровней воды в манометре).
6. Для каждого из пяти проделанных измерений вычислите коэффициент вязкости воздуха по формуле (4) и занесите его в таблицу. Для удобства записи и дальнейших расчетов переведите полученные значения в мкПас.
7. Найдите среднее значение коэффициента вязкости 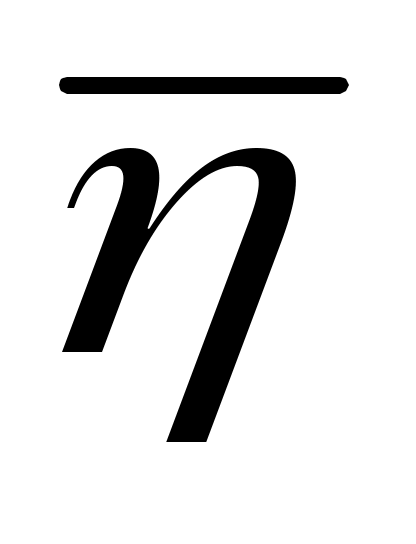 и занесите его в таблицу. Выполните все расчеты, необходимые для оценки случайной погрешности определения величины . Задаваясь доверительной вероятностью = 0,95, рассчитайте погрешность s. и занесите его в таблицу. Выполните все расчеты, необходимые для оценки случайной погрешности определения величины . Задаваясь доверительной вероятностью = 0,95, рассчитайте погрешность s.
8*. Определите абсолютные приборные ошибки прямых измерений уровней воды h, радиуса r и длины L капилляра, объема выливаемой воды V и времени ее истечения t, а также относительные ошибки
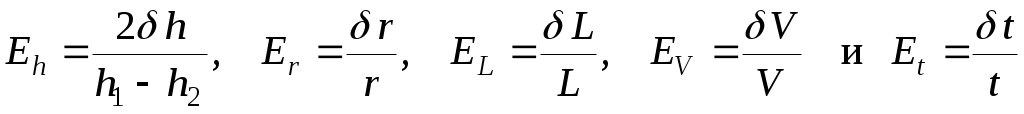 . .
9*. Найдите абсолютную приборную погрешность косвенного измерения коэффициента вязкости . Для этого, если потребуется, используйте формулу
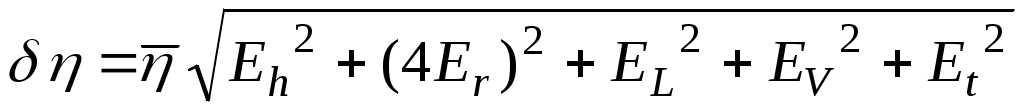 . .
10. Оцените полные абсолютную и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения коэффициента вязкости воздуха. Сравните полученное значение с табличным.
11. Подставляя в формулу (10) среднее значение коэффициента вязкости 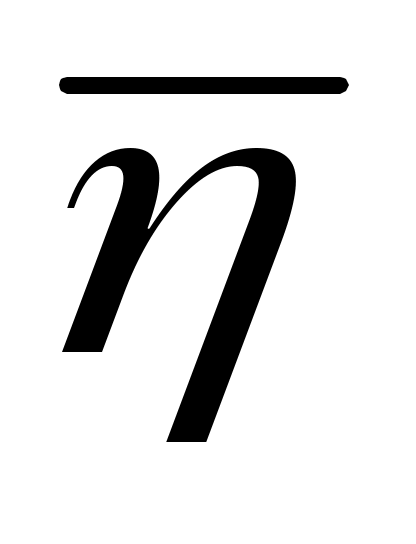 (в Пас), оцените среднюю длину свободного пробега молекул воздуха < l >, а затем по формуле (11) – их эффективный диаметр dэ . Сравните полученные результаты с данными, имеющимися в учебной литературе. Сделайте выводы. (в Пас), оцените среднюю длину свободного пробега молекул воздуха < l >, а затем по формуле (11) – их эффективный диаметр dэ . Сравните полученные результаты с данными, имеющимися в учебной литературе. Сделайте выводы.
Контрольные вопросы
Что называется эффективным диаметром молекул газа?
Как зависит эффективный диаметр от температуры и давления?
Что называется длиной свободного пробега молекул газа?
Как зависит длина свободного пробега от температуры и давления?
Что называется вязкостью газов и от каких параметров она зависит?
Как объяснить различие температурной зависимости динамической вязкости газов и жидкостей?
Получить выражение для определения динамической вязкости газов методом истечения через капилляр.
Какие другие методы применяются для определения динамической вязкости жидкостей и газов?
Что называется кинематической вязкостью и в каких единицах она измеряется?
Какое течение называется ламинарным?
Какой физический смысл имеет число Рейнольдса?
Произведите вывод формулы Гагена-Пуазейля.
Приведите распределение Максвелла молекул идеального газа по скоростям. Обоснуйте основные свойства распределения Максвелла по скоростям.
Опишите изменения кривой распределения Максвелла с увеличением температуры.
Как из распределения Максвелла получают формулы для наивероятнейшей и средней скорости молекул? Сформулируйте эргодическую гипотезу.
Литература:
[3]- §106, 107, 111, 112; [10]- §6.2, 6.3;
|
 Скачать 1.84 Mb.
Скачать 1.84 Mb.
 хема экспериментальной установки
хема экспериментальной установки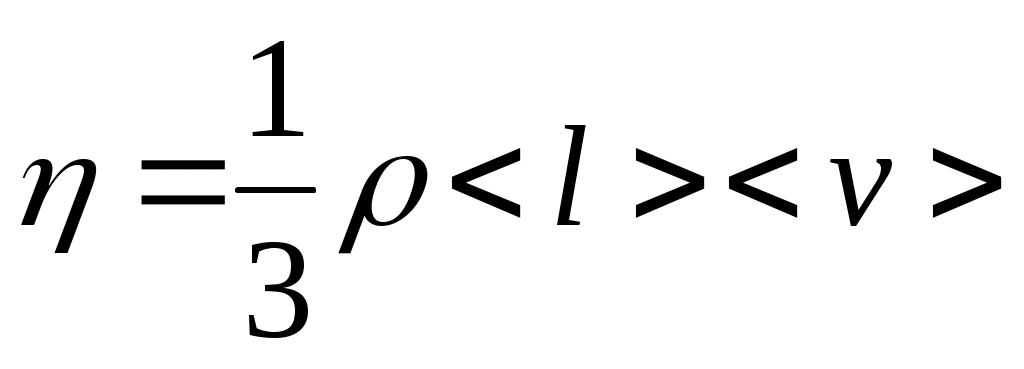 , (6)
, (6)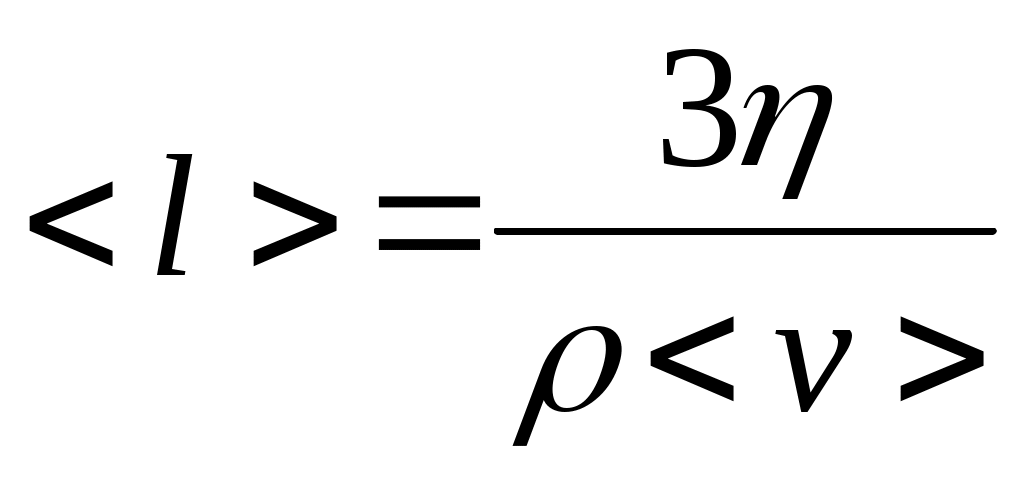 . (7)
. (7)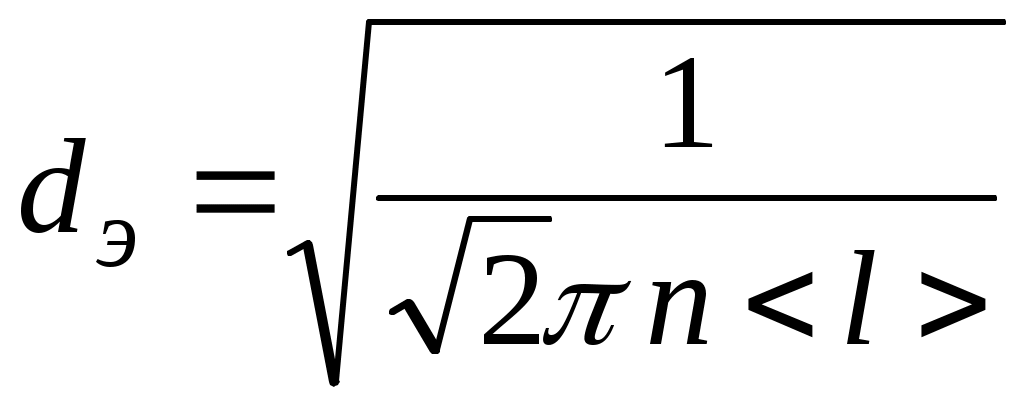 .
.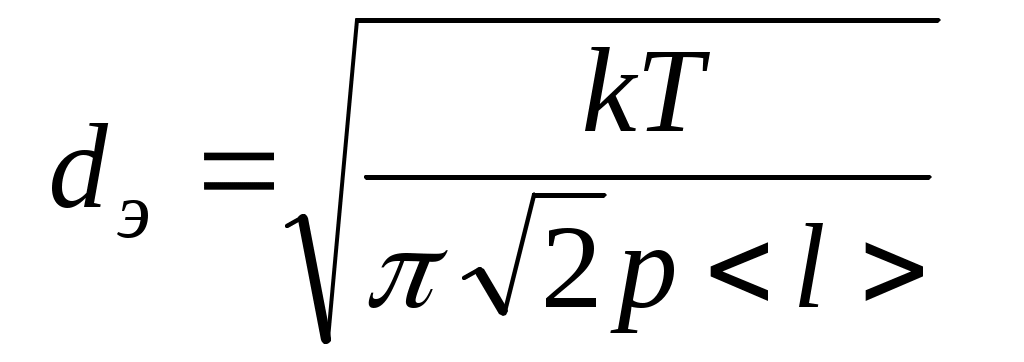 . (11)
. (11)