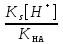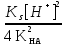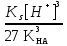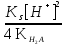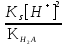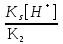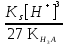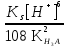Методические указания по общей, неорганической и аналитической химии для студентов и аспирантов технологических и технических специальностей вузов
 Скачать 326.11 Kb. Скачать 326.11 Kb.
|
Для гетерогенного равновесия в кислоте-неокислителеMmАn(т) + 2nH+ (p) молярную растворимость соли, образованной анионом слабой кислоты Н2А, рассчитывают по уравнению sm+n = 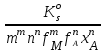 (18) (18)с использованием уравнения (15) при n = 2 для молярной доли хА, где А – S2–, CO 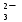 , SO , SO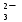 , Se2– и др. , Se2– и др.Приближенные формулы (табл. 1) расчета растворимости могут быть выведены в зависимости от типа стехиометрии соединения MmAn и соотношения величин рК1 и рК2 слабой кислоты Н2А и рН среды. Например, растворимость малорастворимой соли типа МА, образованной катионом М2+ и анионом А2–, определяют по приближенным формулам: а) при pH < pK1 (сульфиды MS, карбонаты MCO3) s [H+] 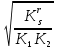 ; (19а) ; (19а)б) при рК1 < pH < pK2 (сульфиты MSO3, селениты MSeO3) s 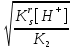 ; (19б) ; (19б)в) при рК2 < pH (сульфаты MSO4, селенаты MSeO4, дихроматы MСr2O7) s 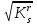 . (19в) . (19в)Расчеты показывают, что растворимость сульфидов MS (M – Pb, Cd, Cu, Hg) сильно (в 107 раз) возрастает при уменьшении рН от 7 до 3 и еще в 200–240 раз при изменении рН от 3 до 1 в основном из-за связывания сульфид-ионов в слабые кислоты HS– и H2S [5]. Растворимость фторидов MF3 (M – Sc, Y, La) при тех же изменениях рН возрастает в 2,3 и 40 раз в основном из-за связывания фторид-ионов в молекулы слабой кислоты HF (см. рисунок). Пример 8. Какую избыточную концентрацию осадителя Na2C2O4 следует создать при рН 3, чтобы растворимость осадка СаС2О4 (К  = 2,3 10–9) не превышала 10–6 моль / л? Ступенчатые константы диссоциации щавелевой кислоты К1 = 5,6 10–2 и К2 = 5,4 10–5 при 25С. Ионную силу раствора не учитывать. = 2,3 10–9) не превышала 10–6 моль / л? Ступенчатые константы диссоциации щавелевой кислоты К1 = 5,6 10–2 и К2 = 5,4 10–5 при 25С. Ионную силу раствора не учитывать.Т а б л и ц а 1 Приближенные формулы для расчета молярной растворимости (s) солей в кислых неокислительных средах
Примечания к таблице: 1. При ионной силе I > 5 10–4 M величина Ks – реальная константа растворимости. 2. КН2А = К1К2, КН3А = К1К2К3. Решение. Для гетерогенного равновесия в кислой среде СаС2О4 (к)  (р) (р)10–6 10–6 C (Na2C2O4) x (C2O 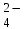 ) )равновесную мольную долю оксалат-ионов вычисляем по формуле (15) при n = 2 и полученное значение 0,05 подставляем в выражение для константы растворимости оксалата кальция: К  = [Ca2+] [C2O = [Ca2+] [C2O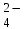 ] = 10–6 C (Na2C2O4) 0,05 = 2,3 10–9. ] = 10–6 C (Na2C2O4) 0,05 = 2,3 10–9.Затем находим С (Na2C2O4) 0,046 моль / л. Пример 9. Может ли образоваться осадок СаF2 (К  = 4,0 10–11) в растворе, содержащем 0,01 моль / л СаCl2, 0,01 моль / л KF и 0,06 моль / л HCl? KHF = 6,2 10–4. Решать с учетом ионной силы раствора. = 4,0 10–11) в растворе, содержащем 0,01 моль / л СаCl2, 0,01 моль / л KF и 0,06 моль / л HCl? KHF = 6,2 10–4. Решать с учетом ионной силы раствора.Решение. Условием образования осадка СаF2 является соотношение [Ca2+] [F–]2 K 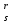 . В кислой среде с гетерогенным равновесием . В кислой среде с гетерогенным равновесиемСа2+ (р) + 2F– (p) конкурирует гомогенное равновесие протонирования фторид-ионов в растворе F– + Н+ Общая ионная сила раствора равна 0,1 моль / л. Тогда коэффициенты активности ионов будут равны f (Ca2+) = 0,405, f (F–) = 0,755 [2], а реальная константа растворимости СаF2 составит 1,7 10–10. Мольную долю анионов F– вычисляем по формуле (15) при n = 1 и [H+] = CHCl = 0,06 M. Полученное значение x (F–) вместе с значениями [Ca2+] = 0,01 М и [F–] = = 0,01 x (F–) используем для определения ИПК = 10–2 (10–2 0,0102)2 = = 1,04 10–10. Так как ИПК = [Ca2+] [F–]2 < K 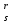 , осадок СаF2 образоваться не может. Решение без учета ионной силы раствора приводит к неверному заключению. , осадок СаF2 образоваться не может. Решение без учета ионной силы раствора приводит к неверному заключению.Пример 10. При какой минимальной концентрации ионов водорода не будет выделяться осадок MnS (K  = 2,5 10–10) в растворе 0,02 М по MnCl2 и 0,06 М по Na2S? Константы ионизации H2S равны К1 = 1,0 10–7 и К2 = = 2,5 10–10) в растворе 0,02 М по MnCl2 и 0,06 М по Na2S? Константы ионизации H2S равны К1 = 1,0 10–7 и К2 == 2,5 10–13 при 25С. Решение. Осадок MnS не будет выделяться при условии [Mn2+] [S2–] < K 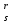 . Рассмотрим гетерогенное равновесие . Рассмотрим гетерогенное равновесиеMnS (к) + 2H+ (p) K 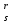 = 1,5 10–9 рН 0,02 М К = 2,5 10–20 = 1,5 10–9 рН 0,02 М К = 2,5 10–20которое смещается вправо при понижении рН раствора. При общей ионной силе электролита 0,24 М коэффициенты активности двухзарядных ионов равны 0,414 [2], а реальная константа растворимости MnS составит 1,5 10–9. Тогда [S2–] < K 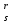 / [Mn2+]. Так как [S2–] = С (Na2S) x (S2–) < 7,3 10–8 М, то согласно формуле (15) при n = 2 получаем уравнение / [Mn2+]. Так как [S2–] = С (Na2S) x (S2–) < 7,3 10–8 М, то согласно формуле (15) при n = 2 получаем уравнение [H+]2 + 10–7 [H+] – 2,05 10–14 = 0, . решая которое, находим [H+]min = 1,02 10–7 М и рН = 6,99. 6.2. Влияние гидролиза ионов осадка При строгом расчете растворимости в чистой воде осадка соли, содержащей анионы слабой кислоты, следует учитывать влияние гидролиза аниона. В результате частичного связывания анионов в недиссоциированные формы кислоты растворимость осадка возрастает. Рассмотрим два основных случая. Если без учета гидролиза растворимость осадка меньше 10–9 М, то ионы ОН–, образующиеся в результате гидролиза соли, практически не нарушают равновесие ионизации воды и [H+] = 10–7 М = const при 25С. Пример 11. Рассчитать влияние гидролиза сульфид-иона на растворимость Cu2S (K  = 2,5 10–48) в чистой воде. Для H2S K1 = 1,0 10–7 и K2 = = 2,5 10–48) в чистой воде. Для H2S K1 = 1,0 10–7 и K2 == 2,5 10–13. Решение. Так как константа K  очень мала, принимаем, что при гидролизе S2– – ионов рН воды практически не изменяется и [H+] = 10–7 М. Тогда [Cu+] = 2s, [S2–] = s x (S2–). По формуле (15) при n = 2 вычисляем x (S2–) = = 1,3 10–6, а затем находим очень мала, принимаем, что при гидролизе S2– – ионов рН воды практически не изменяется и [H+] = 10–7 М. Тогда [Cu+] = 2s, [S2–] = s x (S2–). По формуле (15) при n = 2 вычисляем x (S2–) = = 1,3 10–6, а затем находим s = 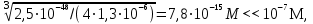 что превышает величину растворимости, вычисленную без учета гидролиза s = 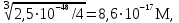 в 91 раз. Рассмотрим теперь случай, когда растворимость осадка соли относительно велика и гидролиз аниона осадка происходит в значительной степени лишь по первой ступени: MmАn + nH2O s ms ns ns Здесь заряды ионов М и НА для простоты опущены. Пренебрегая влиянием равновесия самоионизации воды на концентрацию ОН–, выразим константу гидролиза через константы ионизации слабых электролитов. Тогда получим выражение КГ = K  (MmAn) K (MmAn) K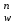 / KHA = (ms)m(ns)n(ns)n (20) / KHA = (ms)m(ns)n(ns)n (20)для расчета молярной растворимости s осадка соли с учетом гидролиза аниона А по первой ступени (Kw – ионное произведение воды). Пример 12. Вычислить растворимость осадка Ва3(PO4)2 в чистой воде с учетом гидролиза аниона. Решение. Учитываем гидролиз по первой ступени с образованием HPO 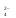 Ва3(PO4)2 + 2H2O 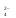 + 2OH– + 2OH–s 3s 2s 2s и, используя значения констант K  = 6 10–39 для фосфата бария и К(HPO = 6 10–39 для фосфата бария и К(HPO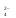 ) = 5,0 10–13, вычисляем растворимость осадка по формуле ) = 5,0 10–13, вычисляем растворимость осадка по формуле s7 = 6 10–39 (10–14)2 / [33 24 (5 10–13)2], откуда s = 5,0 10–7 М, что в 56 раз превышает растворимость соли без учета гидролиза (см. пример 1). Растворимость осадка возрастает и при гидролизе катиона с образованием гидроксокомплексов. При учете этого влияния используются константы устойчивости комплексов. 6.3. Влияние комплексообразования катиона При побочной реакции комплексообразования катиона растворимость осадка соли (гидроксида, оксида) возрастает. В этом случае для расчетов по уравнениям (8) и (4) необходимо знать численное значение мольной доли х(М) свободных (раскомплексованных) катионов М. Мольную долю х(М) вычисляют для известного значения равновесной молярности [L] лиганда по формуле x(M) = [M] / C(M) = [1 + 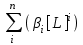 ]–1, (21) ]–1, (21)где C (M) = [M] + [ML] + [ML2] +…+ [MLn] и i – общие концентрационные константы устойчивости (образования) комплексов MLi. Обратную величину 1/х (М) называют функцией закомплексованности. Пример 13. Рассчитать растворимость йодида серебра в 2 М растворе аммиака. ПРт (AgI) = 8,3 10–17; lg 1 = 3,32 и lg 2 = 7,23 для аммиачных комплексов серебра. Решение. С гетерогенным равновесием Ag I (к) конкурируют гомогенные равновесия в растворе Ag+ + NH3 Ag+ + 2NH3  с общими константами 1 и 2. Рассчитаем мольную долю свободных катионов Ag+ по формуле (21) x (Ag+) = (1 + 21 + 222)–1 = 1,5 10–8. Находим условное произведение растворимости AgI ПРу = 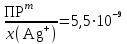 и вычисляем растворимость s = 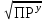 = 7,4 10–5 М. = 7,4 10–5 М.Пример 14. Рассчитать растворимость свежеосажденного основания Mg(OH)2 (ПРт = 6 10–10) в 0,1 М растворе NaOH с учетом ионной силы раствора и образования гидроксокомплекса MgOH+ (1 = 3,6 102). Решение. Растворимость аморфного Mg (OH)2 в чистой воде вычисляем по формуле (4) s = (ПРт / 4)1/3 = 5,3 10–4 М. В щелочном 0,1 М растворе NaOH гетерогенное равновесие Mg(OH)2 (a) s s 2s + 0,1 0,1 сместится влево из-за увеличения концентрации гидроксид-ионов, общих с анионами осадка, и растворимость s основания уменьшится. Рассчитаем сначала величину s без учета комплексообразования, но с учетом ионной силы раствора с использованием формул (7) и (4): I = C (NaOH) = 0,1 M, f (Mg2+) = 0,45, f (OH–) = 0,76 [2], ПРр = 6 10–10 / / (0,45 0,762) = 2,3 10–9, s = ПРр / [OH–]2 = 2,3 10–7 M << s. С учетом гомогенного равновесия в щелочном растворе Mg2+ + OH– с константой 1 найдем мольную долю свободных катионов Mg2+ по формуле (21) x (Mg2+) = 1 / (1 + 1 [OH–] = 2,7 10–2, условное произведение растворимости Mg(OH)2 ПРу = ПРр / x (Mg2+) = 8,6 10–8 и вычислим растворимость s = ПРу / [OH–]2 = 8,6 10–6 М. Полученное значение s в 37 раз превышает величину s, вычисленную без учета комплексообразования катиона магния, но в 62 раза меньше растворимости s в чистой воде (влияние общих ионов ОН– преобладает). 7. ТЕРМОДИНАМИЧЕСКИЙ РАСЧЕТ РАСТВОРИМОСТИ ТВЕРДЫХ ГИДРОКСИДОВ И ОКСИДОВ В ВОДЕ И ЩЕЛОЧНЫХ СРЕДАХ Влияние величины рН на растворимость гидроксидов металлов в водно-щелочной среде представляет интерес при определении условий гидролиза, практически полного осаждения или эффективного маскирования катионов в виде растворимых гидроксокомплексов. В водном растворе, насыщенном относительно малорастворимого гидроксида M(OH)m, устанавливается гетерогенное химическое равновесие M (OH)m (т) термодинамическая константа которого определяется выражением K  = ПРт = а (Мm+) am(OH–) = const (Т). (23) = ПРт = а (Мm+) am(OH–) = const (Т). (23)Значения константы растворимости находят в справочниках, например [2] или рассчитывают [6, 7] с использованием термодинамического соотношения lg K  = – 0,175 G = – 0,175 G , (10,а) , (10,а)где G  – стандартное изменение энергии Гиббса (кДж / моль), которое для процесса растворения (22) вычисляют по уравнению – стандартное изменение энергии Гиббса (кДж / моль), которое для процесса растворения (22) вычисляют по уравнению G  = G = G (Mm+) + mG (Mm+) + mG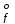 (OH–) – G (OH–) – G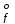 [M(OH)m]. (24) [M(OH)m]. (24)Значения G 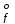 образования ионов в водных растворах приведены в работе [8], величины G образования ионов в водных растворах приведены в работе [8], величины G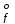 образования аморфных и кристаллических модификаций гидроксидов при 298 К – в справочнике [9]. образования аморфных и кристаллических модификаций гидроксидов при 298 К – в справочнике [9].Молярную растворимость M(OH)m в чистой воде и водно-щелочной среде рассчитывают с учетом ионной силы раствора и образования моноядерных гидроксокомплексов [2] по обобщенному уравнению s = CM = 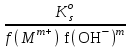 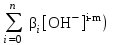 , (25) , (25) где СМ – общая молярность всех химических форм М в насыщенном растворе; о = 1, (1, 2, … , i – общие константы устойчивости гидроксокомплексов MOH(m–1)+ , …, М(ОН) где СМ – общая молярность всех химических форм М в насыщенном растворе; о = 1, (1, 2, … , i – общие константы устойчивости гидроксокомплексов MOH(m–1)+ , …, М(ОН)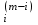 . .7.1. Растворимость в чистой воде Концентрацию свободных анионов ОН– и величину рНо насыщенных растворов гидроксидов или оксидов в чистой воде измеряют рН-метром или находят путем решения системы трех (четырех) уравнений [6, 7] например для гироксидов M(OH)2 или оксидов МО: [M2+] [OH–]2 = K  , , 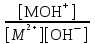 = 1, (26) = 1, (26)2 [M2+] + [MOH+] = [OH–] с использованием метода Кардано для кубического уравнения. В расчетах для неустойчивых твердых гидроксидов, например для ртути (II), и малорастворимых оксидов МО учитывают химические равновесия МО (т) + Н2О (ж) Пример 15. Вычислить рН насыщенного раствора и молярную растворимость s кристаллической -модификации Cd (OH)2 в чистой воде при 25С. K  ( – Cd (OH)2) = 5,4 10–15 [6]. Общие константы устойчивости гидроксокомплексов кадмия (II): 1 = 8,3 103, 2 = 4,5 107, 3 = 5,0 108, ( – Cd (OH)2) = 5,4 10–15 [6]. Общие константы устойчивости гидроксокомплексов кадмия (II): 1 = 8,3 103, 2 = 4,5 107, 3 = 5,0 108,4 = 4,5 108. Решение. В водном растворе Cd (OH)2 преобладают катионы Cd2+, комплексы CdOH+ и анионы ОН–. Равновесную молярность [OH–] = Z и рН найдем, решая систему трех уравнений (26). Получим кубическое уравнение Z3 + pZ + q = 0, где р = – K  1, q = –2 K 1, q = –2 K . Используя метод Кардано, вычисляем дискриминант уравнения D = (p / 3)3 + (q / 2)2. При D = 2,916 10–29 > 0 имеем один действительный корень Z1 = [OH–] = 2,3 10–5 M, откуда рН = 9,36. . Используя метод Кардано, вычисляем дискриминант уравнения D = (p / 3)3 + (q / 2)2. При D = 2,916 10–29 > 0 имеем один действительный корень Z1 = [OH–] = 2,3 10–5 M, откуда рН = 9,36.Молярную растворимость гидроксида кадмия в чистой воде вычисляем по упрощенной формуле (25), так как I < 10–4 M и fi = 1: s = 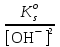 (1 + (1 + 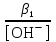 + 2 + 3 [OH–] + 4[OH–]2) = 1,3 10–5 М + 2 + 3 [OH–] + 4[OH–]2) = 1,3 10–5 МРасчет s без учета комплексообразования по формуле (4) дает 1,1 10–5 М (на 20% меньше). Растворимость свежеосажденных аморфных гидроксидов выше, чем кристаллических модификаций. Растворимость последних заметно зависит от структуры, уменьшаясь при переходе к стабильным модификациям [6, 7]. Причиной возникновения метастабильных донных фаз с повышенной энергией и растворимостью является кинетическая заторможенность тех или иных стадий формирования равновесных кристаллических осадков [1]. 7.2. Растворимость в сильнощелочной среде Влияние образования гидроксокомплексов на растворимость гидроксидов и оксидов усиливается при добавлении щелочи. Пример 16. Вычислить молярную растворимость -Cd(OH)2 в 0,01 М и 1 М растворах NaOH с учетом комплексообразования и ионной силы раствора (см. константы K  и i в примере 15). и i в примере 15).Решение. Из-за влияния общих ионов ОН– в сильнощелочной среде NaOH гетерогенное равновесие растворимости должно сместиться в сторону образования осадка гидроксида кадмия. Противоположное (положительное) влияние на растворимость оказывают солевой эффект и особенно образование гидроксокомплексов кадмия (II). При рН = 12 и K 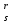 = 9,9 10–15 расчет по формуле s = K = 9,9 10–15 расчет по формуле s = K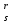 / [OH–]2 дает s = 1,1 10–10 М, а по формуле (25) – 5,0 10–7 М (различие в 4,6 103 раз). / [OH–]2 дает s = 1,1 10–10 М, а по формуле (25) – 5,0 10–7 М (различие в 4,6 103 раз).   = 1,06 K = 1,06 K = 5,7 10–15 расчет растворимости по тем же формулам (4) и (25) дает значения соответственно 5,7 10–15 М и 6 10–6 М (различие в 109 раз). Вместе с тем из-за невысокой прочности гидроксокомплексов кадмия (II) растворимость Cd(OH)2 в 0,01 = 5,7 10–15 расчет растворимости по тем же формулам (4) и (25) дает значения соответственно 5,7 10–15 М и 6 10–6 М (различие в 109 раз). Вместе с тем из-за невысокой прочности гидроксокомплексов кадмия (II) растворимость Cd(OH)2 в 0,01и 1 М растворах NaOH меньше растворимости в чистой воде (s = 1,3 10–5 М). Расчет показывает, что в 5 М растворе NaOH отношение s / s 6 [6], т.е. Cd(OH)2 заметно амфотерен, в отличие от Mg(OH)2 (см. рисунок). Расчеты показывают [6], что при увеличении рН или активной щелочности среды молярная растворимость оснований Mg(OH)2, Са(OH)2, Sr(OH)2 и Ва (OH)2 монотонно уменьшается, следуя приближенному уравнению s = Ks / [OH–]2 (см. рисунок, кривые 2 и 3). При этом эффект сильного понижения растворимости в присутствии общих ОН–-ионов не компенсируется слабым положительным эффектом образования непрочных гидроксокомплексов МОН+ и М(ОН)2. У Sn (OH)2, как и HgO (рисунок, кривая 6), практически отсутствует эффект общих ионов ОН–. Анализ показывает, что условиями отсутствия этого эффекта являются высокие значения константы устойчивости 2 нейтрального комплекса М(ОН)2 и его молярной доли в чисто водном растворе (х 0,9). У Zn(ОН)2 и Со(ОН)2 заметно понижающее (в 2 раза) влияние общих ионов ОН– на растворимость в щелочи, а наиболее сильное влияние (в 350 раз) у Fe(ОН)2 [7]. 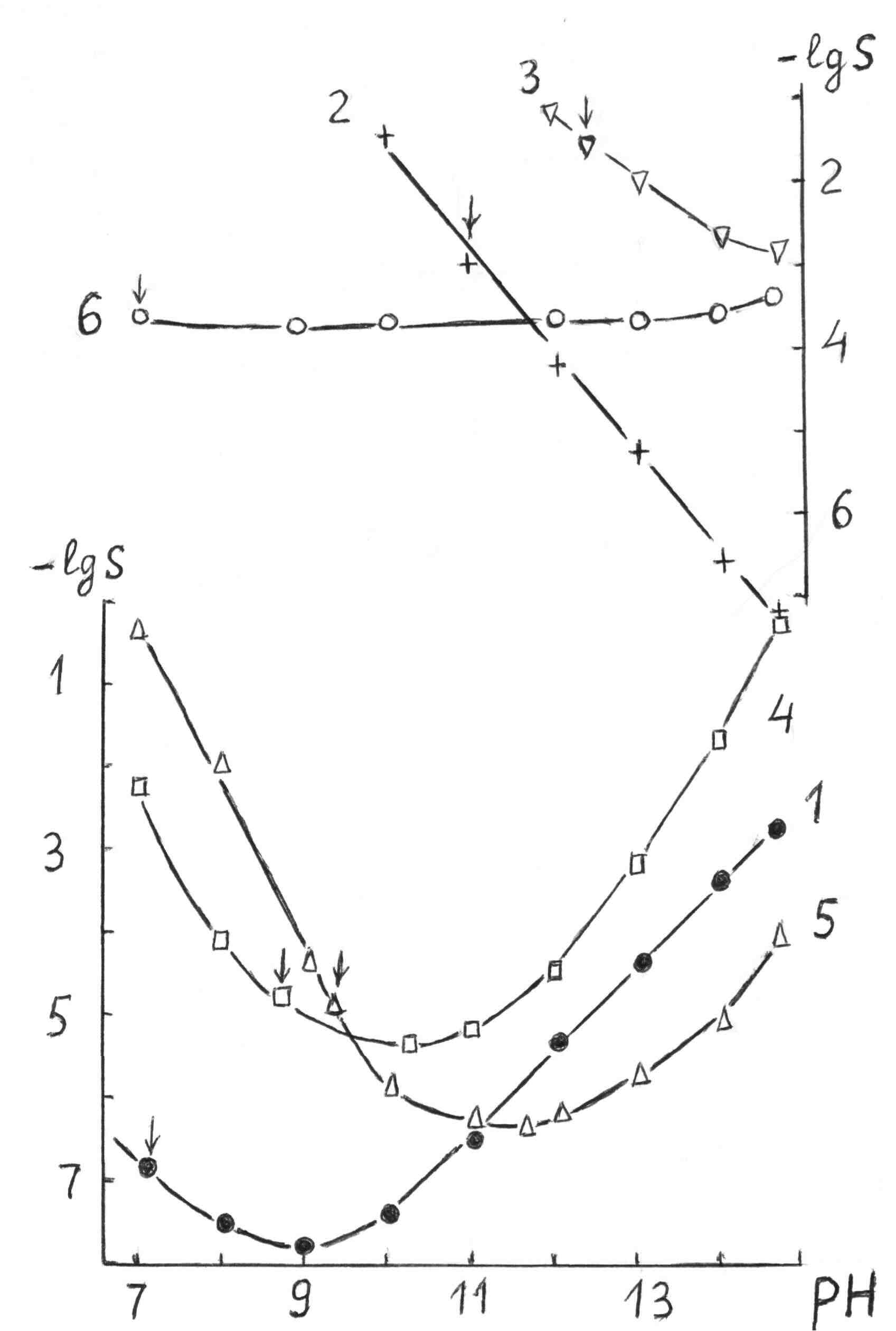 Зависимость растворимости s(моль/л) твердых гидроксидов от водородного показателя рН водно-щелочной среды при t = 25C 1 – -Be(OH)2, 2 – свежеосажденный Mg(OH)2, 3 – Ca(OH)2, 4 – -Zn(OH)2, 5 – -Cd(OH)2, 6 – -HgO. 7.3. Минимальная растворимость амфотерных гидроксидов и оксидов Анализ уравнения (25) приводит к заключению о том, что минимальная растворимость амфотерных гидроксидов М(ОН)n наблюдается при оптимальной концентрации ОН–-ионов, когда среди равновесных частиц в растворе преобладают нейтральные комплексы М(ОН)n. В частности, из условия максимума молярной доли x [M(OH)2] получаем уравнение 24 [OH–]4 + 3 [OH–]3 – 1 [OH–] – 2 = 0, (28) приближенное решение которого с использованием метода Ньютона и констант i позволяет найти оптимальные значения [OH–]opt и затем smin по формуле (25) [6, 7]. Пример 17. С учетом образования гидроксокомплексов рассчитать рН наиболее полного осаждения, минимальную и собственную растворимость в водно-щелочной среде стабильной модификации – Zn (OH)2. K  = == 3,3 10–17 [6]. Общие константы устойчивости гидроксокомплексов цинка (II): 1 = 1,1 106, 2 = 1,3 1011, 3 = 4,0 1013, 4 = 6,3 1014. Решение. Упрощая уравнение (28), получим приближенное уравнение x(3x2 – 1) = 0, откуда x = [OH–] 1,66 10–4 М. Уточняя методом Ньютона найденную величину [OH–] в уравнении (27), получим [OH–]opt = 1,67 10–4 М и рНopt = = 10,22. По уравнению (25) находим smin = 4,9 10–6 моль / л, или 0,5 мг / л. Мольные доли Zn2+, ZnOH+, Zn(OH)2, Zn(OH) 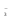 и Zn(OH) и Zn(OH)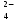 , вычисленные по формуле типа (21), равны соответственно 0,03, 4,73, 90,45, 4,78 и 0,01 мол. %. , вычисленные по формуле типа (21), равны соответственно 0,03, 4,73, 90,45, 4,78 и 0,01 мол. %.Собственная растворимость гидроксида – Zn(OH)2, определяемая равновесной молярностью нейтральных комплексов Zn(OH)2 в растворе, равна Ks2 = 4,4 10–6 моль / л, или 0,905 smin. Расчет растворимости – (ZnOH)2 при рН = 10,22 по формуле (13) без учета образования гидроксокомплексов дает некорректное значение 1,2 10–9 М (в 3,8 103 раз меньше). Оксиды как продукты реальной или условной дегидратации гидроксидов сохраняют химические свойства последних. Оснόвные оксиды щелочных и щелочноземельных металлов химически реагируют с водой, образуя растворимые гидроксиды. Амфотерные оксиды (ZnO, BeO, SnO, PbO, Al2O3, Cr2O3 и др.) в воде практически нерастворимы, реагируют с кислотами и концентрированными щелочами, полностью или заметно растворяясь. Химическая активность и растворимость аморфных оксидов выше, чем прокаленных и стабильных кристаллических оксидов. Гетерогенное химическое равновесие растворимости твердых оксидов МОm/2 (т) + 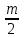 Н2О (ж) Н2О (ж) характеризуется константой K 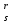 = [Mm+] [OH–]m, как и для гидроксидов. = [Mm+] [OH–]m, как и для гидроксидов.Пример 18. Рассчитать растворимость в чистой воде (s) и минимальную растворимость в водно-щелочной среде (smin) неактивной гексагональной формы ZnO при 25С, используя константу равновесия K  = 1,5 10–17 [1] = 1,5 10–17 [1]для реакции ZnO (к) + H2O (ж) = Zn2+ (р) + 2ОН– (р) и константы устойчивости гидроксокомплексов цинка (см. пример 17). Решение. Как и в примере 15, решаем систему трех уравнений (26) с использованием метода Кардано для кубического уравнения. При дискриминанте D = 5,828 10–35 > 0 имеем один действительный корень Z1 = [OH–] = = 4,78 10–6 М, откуда рН = 8,68 и s = 6,0 10–6 М, или 0,5 мг/л. В водном растворе преобладают Zn(OH)+ (57,5 %), Zn(OH)2 (31,5 %) и Zn2+ (10,9 мол. %). Решая уравнение (28), находим [OH–]opt = 1,67 10–4 М (см. пример 17) и затем по уравнению (25) вычисляем smin = 2,2 10–6 моль / л, или 0,2 мг ZnO / л. 8. КОЛИЧЕСТВЕННАЯ ОЦЕНКА АМФОТЕРНОСТИ ГИДРОКСИДОВ И ОКСИДОВ В ВОДНЫХ СРЕДАХ Амфотерные гидроксиды и оксиды с химическими связями М – О, близкими по степени ионности к связи О – Н, реагируют с кислотами и щелочами, присоединяя или отдавая протоны и гидроксид-ионы, например: М(ОН)2 + Н+ = МОН+ + Н2О, М(ОН)2 + ОН– = М(ОН) 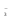 , ,Н2МО2 = Н+ + НМО 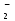 , ,М(ОН)2 = МОН+ + ОН–, МО + 2Н+ = М2+ + Н2О, МО + 2ОН– = МО 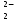 + Н2О. + Н2О.Условием амфотерности оксидов МОm/2 и гидроксидов М(ОН)m является неравенство 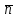 > m, где > m, где 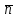 – функция Бьеррума, или среднее лигандное число в моноядерных гидроксокомплексах при рН = 15 [6, 7] вычисляется по формуле – функция Бьеррума, или среднее лигандное число в моноядерных гидроксокомплексах при рН = 15 [6, 7] вычисляется по формуле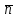 = = 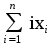 , (30) , (30)в которой мольные доли xi комплексов М(ОН)i определяются с использованием констант устойчивости i и [OH–]. В частности, условие амфотерности 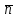 > 2 выполняется для оксидов и гидроксидов Ве, Zn, Cd, Hg, Sn, Pb, Mn – Cu [7] и не выполняется для соединений Mg – Ba [6]. > 2 выполняется для оксидов и гидроксидов Ве, Zn, Cd, Hg, Sn, Pb, Mn – Cu [7] и не выполняется для соединений Mg – Ba [6].Для количественной оценки амфотерности гидроксидов и оксидов предложено в [6, 7] использовать величину отношения (А > 1) их молярных растворимостей в сильнощелочной среде с рН = 14,7 (5 М раствор NaOH) и в чистой воде (табл. 2). Пример 19. Оценить параметр амфотерности А неактивной гексагональной формы ZnO (K  = 1,5 10–17, s = 6,0 10–6 М, см. пример 18) в водно-щелочной среде при 25С. = 1,5 10–17, s = 6,0 10–6 М, см. пример 18) в водно-щелочной среде при 25С.Решение. Условие амфотерности ZnO и Zn(OH)2 выполнено ( 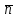 = == 3,99 > 2). Для оценки параметра амфотерности А в виде отношения s (рН = 14,7) / s (H2O) вычислим молярную растворимость ZnO (к) в водной среде с рН = 14,7 по уравнению (25), используя [ОН–] = 5 M, f (Zn2+) f(OH–)2 1 и константы устойчивости i, приведенные в примере 17: s (рН = 14,7) = 1,5 10–17 (0,04 + 2,2 105 + 1,26 1011 + 1,99 1014 + + 1,58 1016) = 0,24 моль / л. 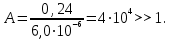 При рН = 14,7 преобладает комплекс Zn(OH) 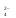 (98,8%). (98,8%).Из табл. 2 видно, что параметр амфотерности А гидроксидов М(ОН)2 изменяется в широком диапазоне. Наиболее высокая растворимость при рН = 14,7 у амфотерных гидроксидов олова (II) и цинка (0,76 и 0,52 моль / л при 25С). Согласно [2] полное растворение выпавшего осадка этих гидроксидов происходит при рН = 13,5 и 12,5, а Al(OH)3 – при рН = 10,8. Несмотря на высокие значения параметра А, растворимость гидроксидов бериллия и меди (II) в 5 М NaOH мала (1 10–3 и 0,015 моль / л) из-за низких величин K  и s (табл. 2). и s (табл. 2).Увеличение растворимости большинства амфотерных гидроксидов наблюдается при нагревании и повышении концентрации щелочи NaOH (до 19 моль / л) или КОН (до 14 моль / л), а также в кислых средах [1, 2]. Т а б л и ц а 2 Рассчитанные термодинамические параметры растворения стабильных кристаллических гидроксидов в воде и щелочи при 25С [6, 7]
Библиографический список 1. Кумок В.Н., Кулешова О.М., Карабин Л.А. Произведения растворимости. Новосибирск: Наука, 1983. 267 с. 2. Лурье Ю.Ю. Справочник по аналитической химии. М.: Химия, 1989. 448 с. 3. Дорохова Е.Н., Прохорова Г.В. Задачи и вопросы по аналитической химии. М.: Изд. МГУ, 1984. 216 с. 4. Булатов М.И. Расчеты равновесий в аналитической химии. Л.: Химия. 1984. 184 с. 5. Школьников Е.В. Термодинамический расчет растворимости кристаллических галогенидов и сульфидов в воде и кислых средах // Журнал прикладной химии. 2003. Т. 76. № 11. С. 1785–1787. 6. Школьников Е.В. Термодинамический расчет растворимости твердых гидроксидов М(ОН)2 в воде и щелочных средах // Журнал прикладной химии. 2004. Т. 77. № 8. С. 1271–1274. 7. Школьников Е.В. Термодинамическая характеристика амфотерности гидроксидов М(ОН)2 в водных средах // Журнал прикладной химии. 2005. Т. 78. № 11. С. 1819–1823. 8. Васильев В.П. Термодинамические свойства растворов электролитов. М.: Высшая школа, 1982. 320 с. 9. Термодинамические свойства индивидуальных веществ / Под ред. В.П. Глушко. М.: Наука, 1979–1981. Т. 1–4. Оглавление 1. Растворимость твердых электролитов в воде 3 2. Произведение растворимости 4 3. Способы выражения произведения растворимости 6 4. Растворимость осадков в присутствии общих ионов 8 5. Растворимость осадков с учетом влияния ионной силы раствора 9 6. Влияние конкурирующих равновесий протонирования и комплексообразования на растворимость осадков 11 6.1. Влияние рН кислой водной среды 11 6.2. Влияние гидролиза ионов осадка 16 6.3. Влияние комплексообразования катиона 17 7. Термодинамический расчет растворимости твердых гидроксидов и оксидов в воде и щелочных средах 19 7.1. Растворимость в чистой воде 20 7.2. Растворимость в сильнощелочной среде 21 7.3. Минимальная растворимость амфотерных гидроксидов и оксидов 23 8. Количественная оценка амфотерности гидроксидов и оксидов в водных средах 25 Библиографический список 27 Евгений Васильевич Школьников РАСЧЕТЫ РАСТВОРИМОСТИ СОЛЕЙ, ГИДРОКСИДОВ И ОКСИДОВ В ВОДНЫХ СРЕДАХМетодические указания по общей, неорганической и аналитической химии для студентов и аспирантов технологических и технических специальностей вузов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||