Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
| | 32 | 4,15 | 3,30 | 2,90 | 2,67 | 2,51 | 2,40 | 2,32 | 2,25 | 2,19 | | 34 | 4,13 | 3,28 | 2,88 | 2,65 | 2,49 | 2,38 | 2,30 | 2,23 | 2,17 | | 36 | 4,11 | 3,26 | 2,86 | 2,63 | 2,48 | 2,36 | 3,28 | 2,21 | 2,15 | | 38 | 4,10 | 3,25 | 2,85 | 2,62 | 2,46 | 2,35 | 2,26 | 2,19 | 2,14 | | 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | | 42 | 4,07 | 3,22 | 2,83 | 2,59 | 2,44 | 2,32 | 2,24 | 2,17 | 2,11 | | 44 | 4,06 | 3,21 | 2,82 | 2,58 | 2,43 | 2,31 | 2,23 | 2,16 | 2,10 | | 46 | 4,05 | 3,20 | 2,81 | 2,57 | 2,42 | 2,30 | 2,22 | 2,14 | 2,09 | | 48 | 4,04 | 3,19 | 2,80 | 2,56 | 2,41 | 2,30 | 2,21 | 2,14 | 2,08 | | 50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,20 | 2,13 | 2,07 | | 55 | 4,02 | 3,17 | 2,78 | 2,54 | 2,38 | 2,27 | 2,18 | 2,11 | 2,05 | | 60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | | 65 | 3,99 | 3,14 | 2,75 | 2,51 | 2,36 | 2,24 | 2,15 | 2,08 | 2,02 | | 70 | 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,14 | 2,07 | 2,01 | | Продолжение приложения 4 | | | d.f.1 - степени свободы для большего среднего квадрата | | d.f.2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | 80 | 3,86 | 3,11 | 2,72 | 2,48 | 2,33 | 2,21 | 2,12 | 2,05 | 1,99 | | 100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,10 | 2,03 | 1,97 | | 125 | 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,08 | 2,01 | 1,95 | | 150 | 3,91 | 3,06 | 2,67 | 2,43 | 2,27 | 2,16 | 2,07 | 2,00 | 1,94 | | 200 | 3,89 | 3,04 | 2,65 | 2,41 | 2,26 | 2,14 | 2,05 | 1,98 | 1,92 | | 400 | 3,86 | 3,02 | 2,62 | 2,39 | 2,23 | 2,12 | 2,03 | 1,96 | 1,90 | | 1000 | 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 2,02 | 1,95 | 1,89 | | | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 2,01 | 1,94 | 1,88 | | | | | | | | | | | | | | d.f.1 - степени свободы для большего среднего квадрата | d.f.2 | 10 | 11 | 12 | 14 | 16 | 20 | 30 | 40 | 50 | | 1 | 242 | 243 | 244 | 245 | 246 | 248 | 250 | 251 | 252 | 254 | 2 | 19,39 | 19,40 | 19,41 | 19,42 | 19,43 | 19,44 | 19,46 | 19,47 | 19,47 | 19,50 | 3 | 8,78 | 8,76 | 8,74 | 8,71 | 8,69 | 8,66 | 8,62 | 8,60 | 8,58 | 8,53 | 4 | 5,96 | 5,93 | 5,91 | 5,87 | 5,84 | 5,80 | 5,74 | 5,71 | 5,70 | 5,63 | 5 | 4,74 | 4,70 | 4,68 | 4,64 | 4,60 | 4,56 | 4,50 | 4,46 | 4,44 | 4,36 | 6 | 4,06 | 4,03 | 4,00 | 3,96 | 3,92 | 3,87 | 3,81 | 3,77 | 3,75 | 3,67 | 7 | 3,63 | 3,60 | 3,57 | 3,52 | 3,49 | 3,44 | 3,38 | 3,34 | 3,32 | 3,23 | 8 | 3,34 | 3,31 | 3,28 | 3,23 | 3,20 | 3,15 | 3,08 | 3,05 | 3,03 | 2,93 | 9 | 3,13 | 3,10 | 3,07 | 3,02 | 2,98 | 2,93 | 2,86 | 2,82 | 2,80 | 2,71 | 10 | 2,97 | 2,94 | 2,91 | 2,86 | 2,82 | 2,77 | 2,70 | 2,67 | 2,64 | 2,54 | 11 | 2,86 | 2,82 | 2,79 | 2,74 | 2,70 | 2,65 | 2,57 | 2,53 | 2,50 | 2,40 | 12 | 2,76 | 2,72 | 2,69 | 2,64 | 2,60 | 2,54 | 2,46 | 2,42 | 2,40 | 2,30 | 13 | 2,67 | 2,63 | 2,60 | 2,55 | 2,51 | 2,46 | 2,38 | 2,34 | 2,32 | 2,21 | 14 | 2,60 | 2,56 | 2,53 | 2,48 | 2,44 | 2,39 | 2,31 | 2,27 | 2,24 | 2,13 | 15 | 2,55 | 2,51 | 2,48 | 2,43 | 2,39 | 2,33 | 2,25 | 2,21 | 2,18 | 2,07 | 16 | 2,49 | 2,45 | 2,42 | 2,37 | 2,33 | 2,28 | 2,20 | 2,16 | 2,13 | 2,01 | 17 | 2,45 | 2,41 | 2,38 | 2,33 | 2,29 | 2,23 | 2,15 | 2,11 | 2,08 | 1,96 | 18 | 2,41 | 2,37 | 2,34 | 2,29 | 2,25 | 2,19 | 2,11 | 2,07 | 2,04 | 1,92 | 19 | 2,38 | 2,34 | 2,31 | 2,26 | 2,21 | 2,15 | 2,07 | 2,02 | 2,00 | 1,88 | 20 | 2,35 | 2,31 | 2,28 | 2,23 | 2,18 | 2,12 | 2,04 | 1,99 | 1,96 | 1,84 | 21 | 2,32 | 2,28 | 2,25 | 2,20 | 2,15 | 2,09 | 2,00 | 1,96 | 1,93 | 1,81 | 22 | 2,30 | 2,26 | 2,23 | 2,18 | 2,13 | 2,07 | 1,98 | 1,93 | 1,91 | 1,78 | 23 | 2,28 | 2,24 | 2,20 | 2,14 | 2,10 | 2,04 | 1,96 | 1,91 | 1,88 | 1,76 | 24 | 2,26 | 2,22 | 2,18 | 2,13 | 2,09 | 2,02 | 1,94 | 1,89 | 1,86 | 1,73 | 25 | 2,24 | 2,20 | 2,16 | 2,11 | 2,06 | 2,00 | 1,92 | 1,87 | 1,84 | 1,71 | 26 | 2,22 | 2,18 | 2,15 | 2,10 | 2,05 | 1,99 | 1,90 | 1,85 | 1,82 | 1,69 | 27 | 2,20 | 2,16 | 2,13 | 2,08 | 2,03 | 1,97 | 1,88 | 1,84 | 1,80 | 1,67 | 28 | 2,19 | 2,15 | 2,12 | 2,06 | 2,02 | 1,96 | 1,87 | 1,81 | 1,78 | 1,65 | 29 | 2,18 | 2,14 | 2,10 | 2,05 | 2,00 | 1,94 | 1,85 | 1,80 | 1,77 | 1,64 | 30 | 2,16 | 2,12 | 2,09 | 2,04 | 1,99 | 1,93 | 1,84 | 1,79 | 1,76 | 1,62 | 32 | 2,14 | 2,10 | 2,07 | 2,02 | 1,97 | 1,91 | 1,82 | 1,76 | 1,74 | 1,69 | 34 | 2,12 | 2,08 | 2,05 | 2,00 | 1,95 | 1,89 | 1,80 | 1,74 | 1,71 | 1,57 | 36 | 2,10 | 2,06 | 2,03 | 1,98 | 1,93 | 1,87 | 1,78 | 1,72 | 1,69 | 1,55 | 38 | 2,09 | 2,05 | 2,02 | 1,96 | 1,92 | 1,85 | 1,76 | 1,71 | 1,67 | 1,53 Продолжение приложения 4
Приложение 5 Алгоритм расчета табличного значения t-критерия Стьюдента при разных условиях формирования выборок (λ - уровень значимости,d.f.- число степеней свободы вариации)
1 Несмещенную оценку дисперсии необходимо рассчитывать, прежде всего, для совокупностей менее 30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

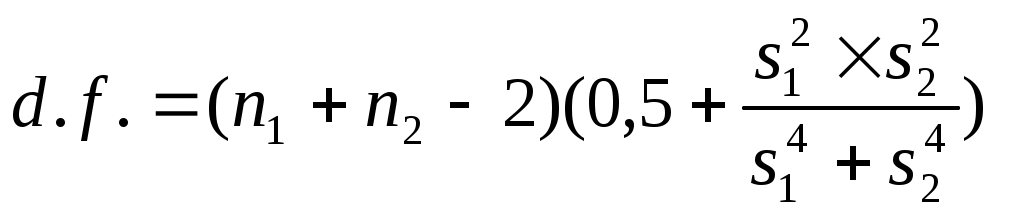
 ,
,