Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb.
|
|
Все коэффициенты чистой регрессии имеют Р-значения меньше принятого уровня значимости (0,05), следовательно, признаются достоверными. Выборочная модель множественной линейной регрессии может быть записана в виде:   .2. Оценим показатели тесноты связи. EXCEL автоматически рассчитал коэффициенты множественной корреляции (множественный R) и детерминации (R-квадрат), а также скорректированный коэффициент детерминации (нормированный R-квадрат) (табл. 4.2.1 - б). Напомним, что коэффициент множественной детерминации определяется по формуле:  , где W – общий,  – воспроизведенный уравнением, а Wе– остаточный объем вариации.Множественный коэффициент корреляции (R) и скорректированный коэффициент детерминации: (  ): ,  где n – число наблюдений (n=68), p – число регрессоров (факторов) в уравнении, в нашем случае p=4). чувствителен к увеличению числа регрессоров и уменьшению числа наблюдений, чем больше факторов включено в модель и чем меньше число наблюдений, тем больше различия между множественным коэффициентом детерминации и скорректированной его величиной.Мы получили следующие показатели тесноты связи: R2=0,907,  , R=0,953. Между коэффициентом детерминации и скорректированным коэффициентом существуют различия (0,6%). Так как число наблюдений достаточно велико, то различия не столь существенны, и поэтому можно использовать R2и Rдля оценки тесноты связи. Множественный коэффициент корреляции (R = 0,953) свидетельствует об очень тесной связи между факторами и результатом, множественный коэффициент детерминации показывает, что 90,7 % вариации стоимости квартир связано с включенными в модель факторами. Полученные выводы следует оценить на достовернгость: насколько они существенны для генеральной совокупности, поскольку мы получили лишь выборочные показатели связи и выборочное уравнение регрессии.3. Дадим оценку значимости уравнения в целом, условного начала и коэффициентов чистой регрессии. Оценка значимости уравнения в целом проводится на основе дисперсионного анализа. Предположим, что уравнение не значимо для генеральной совокупности (Н0:  ). В качестве альтернативной гипотезы выдвинем предположение о значимости уравнения (НА: ). Проверим эти гипотезы на 5% уровне значимости. В качестве критерия выберем критерий F-Фишера, его фактическое значение определяется по формуле. = Фактическое значение критерия равно 154,29 (табл.. 4.2.1-б). Сравним его с критическим значением  , которое можно найти, используя встроенную функцию FРАСПОБР( ) или по таблице (приложение 4). В нашем случае:  =FРАСПОБР(0,05;4;63)=2,52. Поскольку фактическое значение превышает критическое, принимаем гипотезу о значимости уравнения регрессии в целом для генеральной совокупности. Можно также оценить значимость критерия (фактического значения): из табл. 4.2.1-б видно, что критерий значим уже при 8,377 ∙10-32 %-ой области, что гораздо меньше принятой нами 5%-ой. Следовательно, уравнение в целом значимо. Это означает тот факт, что в уравнении есть хотя бы один статистически достоверный параметр взаимосвязи, но возможно не значим какой-либо из его параметров для генеральной совокупности. Выдвинем рабочую гипотезу о равенстве нулю всех параметров уравнения в генеральной совокупности и альтернативную ей: H0: HА: 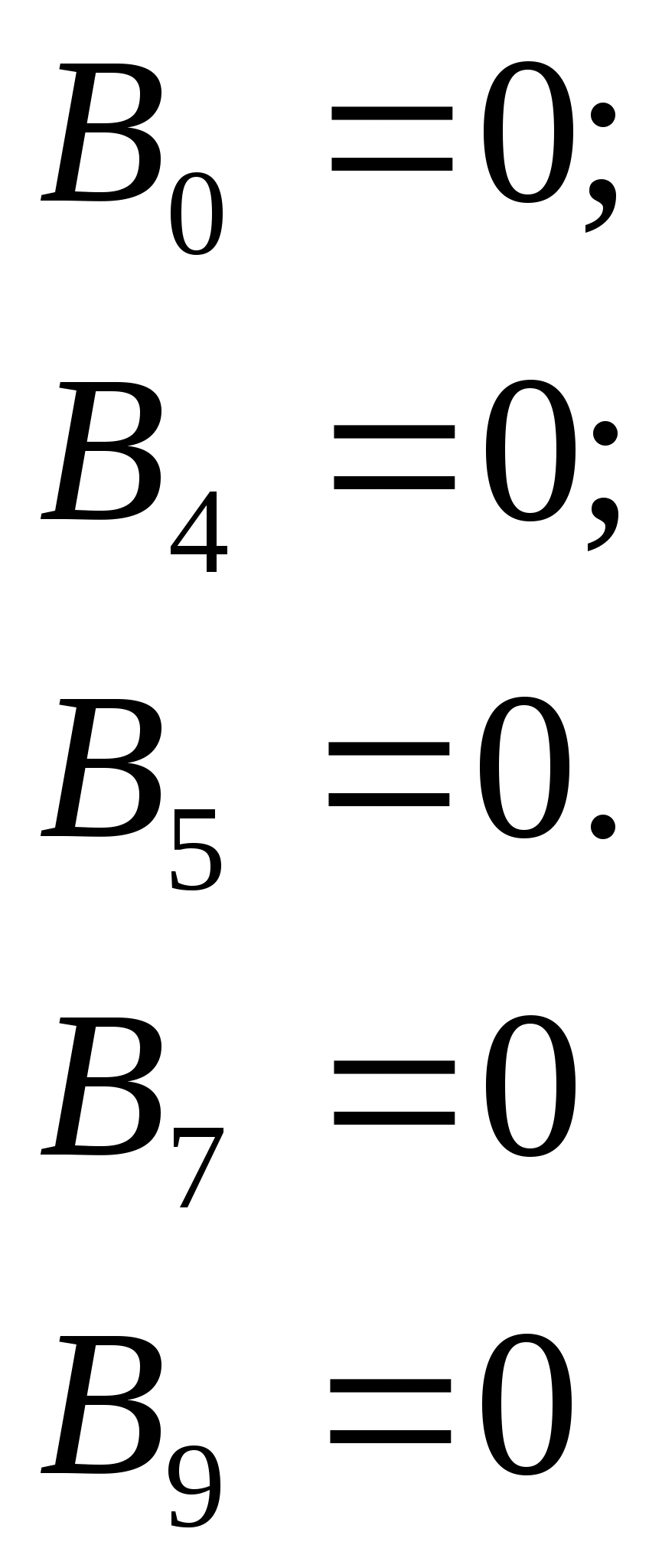 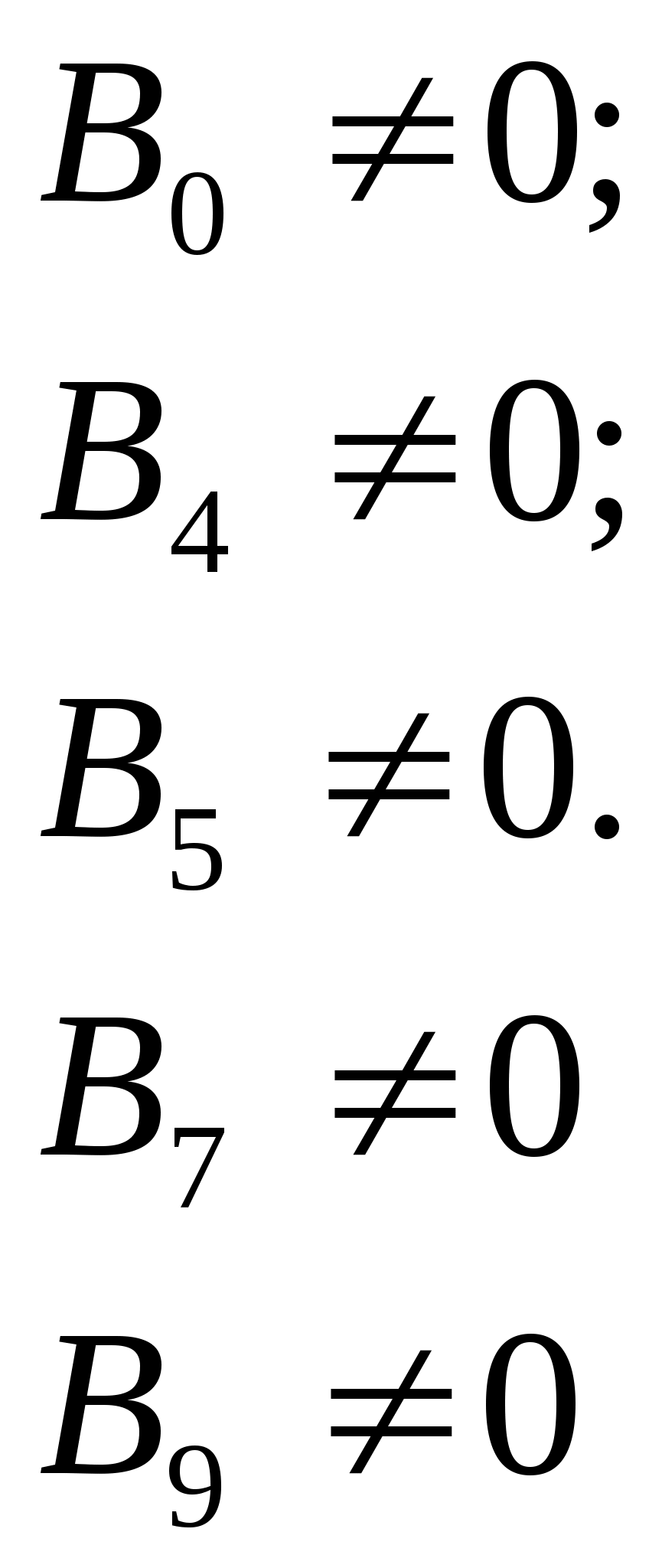 Гипотезы проверим на 5% уровне значимости. Для проверки гипотез используется критерием t-нормального распределения (приложение 2), поскольку выборка по своему объему является большой. Если выборка является малой, то для проверки гипотезы следует использовать критерий Стьюдента. Напомним, что найти его критическое значение можно, используя функцию СТЬЮДРАСПОБР(  ;n-p-1) или данные таблицы в приложении 3.Фактические значения критерия t определяется по формуле:  .EXCEL автоматически производит расчет фактических значений критерия t и его значимости, средних ошибок, доверительных интервалов (на 95%-ом уровне вероятности суждения) для каждого из параметров уравнения регрессии ( табл. 4.2.1-б, последняя ее часть). Как видно из таблицы, свободный член уравнения регрессии (у-пересечение) оказался статистически недостоверен, так как его уровень значимости Р=0,06 выше принятого (0,05). Это означает, что истинное значение этого параметра в генеральной совокупности может быть как выше, так и ниже нуля : от -0,045 до 1,7. Все коэффициенты регрессии оказались достоверными: Р-значение ниже принятого уровня значимости. Следовательно, можно дать точечную и интервальную оценку параметрам в генеральной совокупности. Точечная оценка позволяет предположить, что генеральное уравнение будет иметь параметры при соответствующих размерах средних ошибок (табл. 4.2.2).Табл. 4.2.2. Точечная оценка коэффициентов чистой регрессии.
Проведем интервальную оценку параметров:  .Для нашей модели с уровнем вероятности суждения 95% можно утверждать, что параметры генерального уравнения множественной регрессии попадут в следующие интервалы (табл. 4.2.3). Таблица 4.2.3. Интервальная оценка параметров регрессии
|