Контрольная работа МСС строительство. Методические указания по выполнению контрольной работы по дисциплине Метрология, стандартизация, сертификация и управление качеством

• Название: Методические указания по выполнению контрольной работы по дисциплине Метрология, стандартизация, сертификация и управление качеством
• Дата: 15.04.2021
• Размер: 270.5 Kb.
• Имя файла: Контрольная работа МСС строительство.doc
• Тип: Методические указания; #195189
• страница: 4 из 4

Пример выполнениЯ задания № 2

Выполнено 150 измерений диаметра аттестованного образца микрометром нулевого класса, это количество измерений образует генеральную совокупность. Случайным образом было отобрано 50 результатов измерений из генеральной совокупности, таким образом, получили выборочную совокупность, которую обычно называют выборкой.

Результаты измерений, образующих выборочную совокупность сведены в табл. 2.

Таблица 2

Результаты измерений, мм
1	2	3	4	5
7,971	7,965	7,969	7,967	7,976
7,974	7,969	7,971	7,975	7,969
7,973	7,973	7,968	7,972	7,974
7,965	7,970	7,963	7,964	7,969
7,966	7,971	7,967	7,978	7,972
7,973	7,973	7,966	7,971	7,975
7,968	7,977	7,970	7,974	7,971
7,967	7,974	7,968	7,970	7,972
7,977	7,975	7,971	7,971	7,973
7,964	7,971	7,972	7,968	7,973

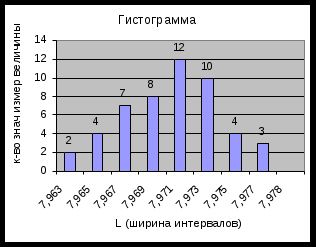
Для построения гистограммы выполним следующее:

1. 
   Определим размах точечных значений результата измерений по формуле:
   

R = X_max - X_min,

где: R– размах точечных значений результата измерений, мм;

X_max – наибольшее значение измеренной физической величины, мм;

X_min – наименьшее значение измеренной физической величины, мм.

R = 7,978мм – 7,963мм = 0,015мм.

2. 
   Затем определим число интервалов по формуле:
   

К = 5 lgn,

где: К – число интервалов;

n– количество измерений физической величины.

К = 5 lg 50 = 8,49485.

Принимаем количество интервалов, равным 8.

3. 
   Определим ширину интервалов:
   

,

0,001648. мм

Так как результаты измерений записаны с точностью до 0,001мм, то ширину интервала принимаем равной 0,002 мм.

4. Для расчета границ интервалов гистограммы применим формулу:

L = X_min + dm,

где: X_min– наименьшее значение измеренной физической величины;

d– ширина интервала;

m– номер интервала.
L₁ = 7,963мм – 7,965мм; (X_min + dm = 7,963 + 0,002  1 = 7,965);

L₂ = 7,965мм – 7,967мм; (X_min + dm = 7,963 + 0,002  2 = 7,967);

L₃ = 7,967мм – 7,969мм;(X_min + dm = 7,963 + 0,002  3 = 7,969);

L₄ = 7,969мм – 7,971мм; (X_min + dm = 7,963 + 0,002  4 = 7,971);

L₅ = 7,971мм – 7,973мм; (X_min + dm = 7,963 + 0,002  5 = 7,973);

L₆ = 7,973мм – 7,975мм; (X_min + dm = 7,963 + 0,002  6 = 7,975);

L₇ = 7,975мм – 7,977мм; (X_min + dm = 7,963 + 0,002  7 = 7,977);

L₈ = 7,977мм – 7,979мм; (X_min + dm = 7,963 + 0,002  8 = 7,979).
Однако, максимальный результат измерения равен 7,978 мм, следовательно и ширина 8-го интервала будет равной 7,977мм - 7,978мм. Это произошло из-за того, что ширину интервалов мы округлили до 0,002мм.

5. Определим среднее арифметическое значение физической величины, являющееся оценкой математического ожидания, по формуле: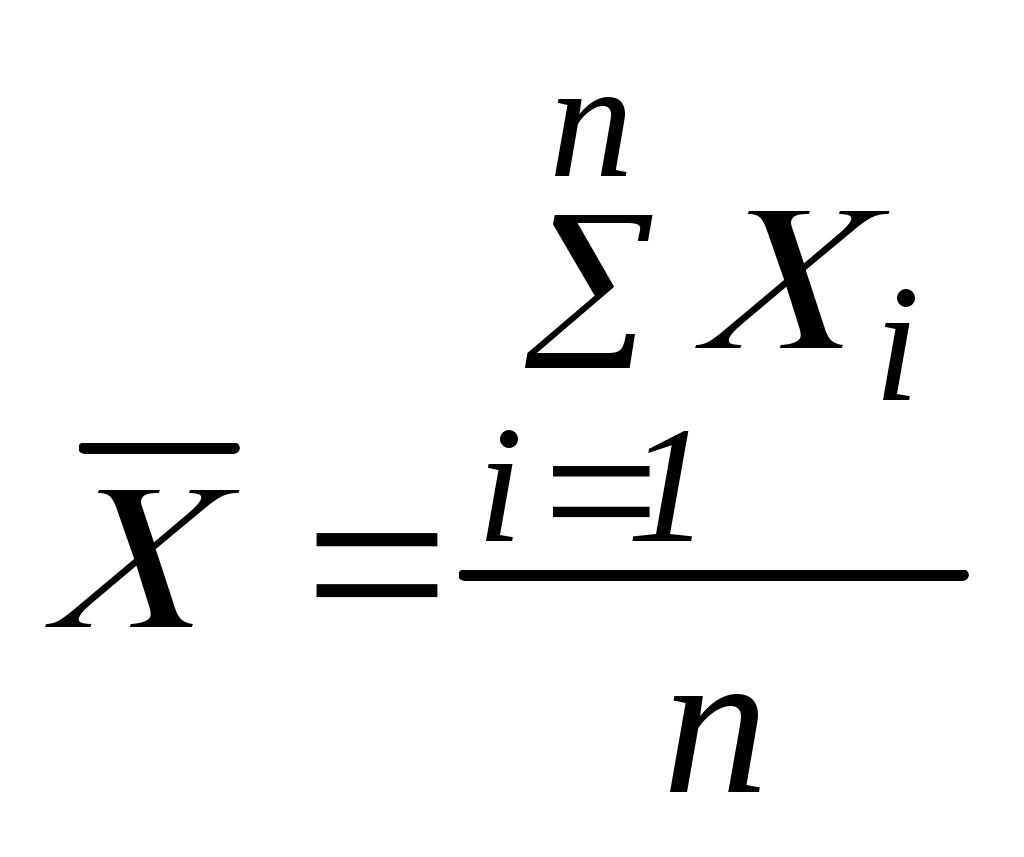

,

где: – среднее арифметическое значение физической величины;

X_i – результат i- го измерения физической величины;

– сумма значений измеряемой физической величины:

мм.

6. Определим статистическое среднее квадратическое отклонение (найденное на основе полученных измерений) по формуле: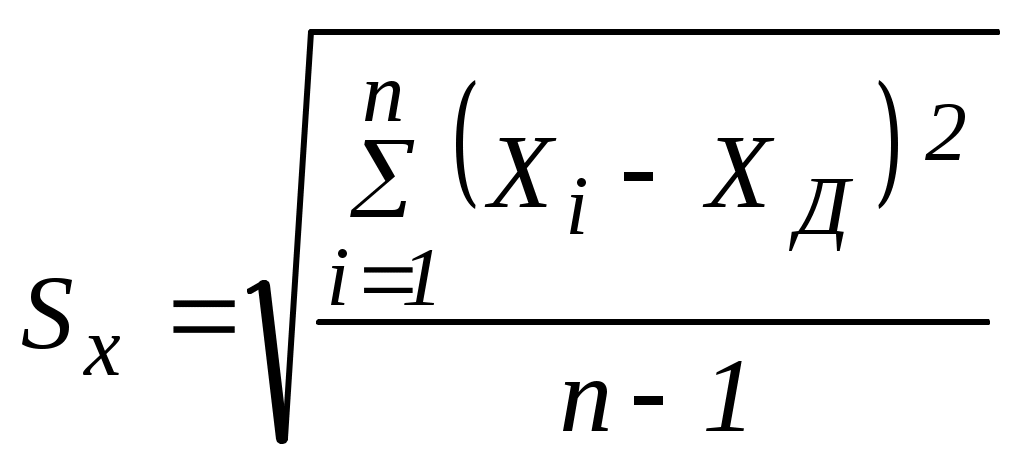

.

Предварительно определим сумму квадратов отклонений от действительного значения физической величины и расчетные данные сведем в табл. 3:

.

Таблица 3

0,0000000324	0,0000338724	0,0000033124	0,0000145924	0,0000268324
0,0000101124	0,0000033124	0,0000000324	0,0000174224	0,0000033124
0,0000047524	0,0000047524	0,0000079524	0,0000013924	0,0000101124
0,0000338724	0,0000006724	0,0000033124	0,0000465224	0,0000033124
0,0000232324	0,0000000324	0,0000145924	0,0000515524	0,0000013924
0,0000047524	0,0000047524	0,0000232324	0,0000000324	0,0000174224
0,0000079524	0,0000381924	0,0000006724	0,0000101124	0,0000000324
0,0000145924	0,0000101124	0,0000079524	0,0000006724	0,0000013924
0,0000381924	0,0000174224	0,0000000324	0,0000000324	0,0000047524
0,0000465224	0,0000000324	0,0000013924	0,0000079524	0,0000047524

Определяем среднее квадратическое отклонение:

.

Определяем статистическое среднее квадратическое отклонение физической величины:

.

7. Теперь выполним оценку погрешности измерений.

Для этого выбираем по таблице доверительных вероятностей  = 0,95 и соответствующее ей значение квантиля закона распределения случайной величиныt_ = 1,960.

Таблица доверительных вероятностей

Доверительная вероятность (надежность) 	0,80	0,90	0,95	0,99	0,999
Значение квантиля закона распределения t	1.282	1.645	1.960	2.576	3.290

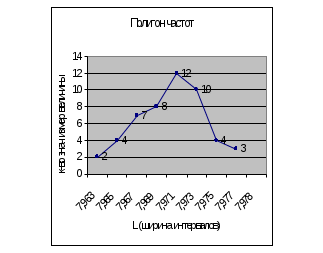
Примечание: обычно надежность оценки задается предварительно, причем в качестве  берут число, близкое к единице.
Затем определим величину абсолютной погрешности измерения по следующей формуле:

,

где:  – величина погрешности измерения физической величины;

_х – теоретическое среднее квадратическое отклонение;

t_– квантиль закона распределения.

.

Величина погрешности равна 0,00111.

И, наконец, выполним оценку доверительного интервала, в котором с данной доверительной вероятностью неизвестное истинное значение измеряемой величины совместимо с величиной ;

за действительное значение физической величины принимаем среднее арифметическое значение выборки :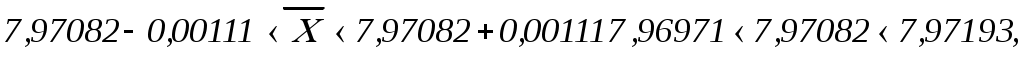



где: – среднее арифметическое значение физической величины;

t_– квантиль закона распределения;

n– количество измерений физической величины.

При определении условий существования полученного доверительного интервала мы предположили, что дисперсия нормального закона распределения, а, следовательно, и среднее квадратическое отклонение _х известны. На практике мы можем воспользоваться лишь статистически найденным значением оценки среднего квадратического отклонения, то есть значением S_x: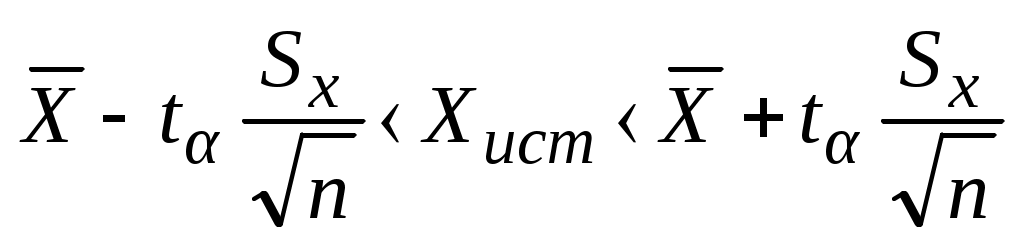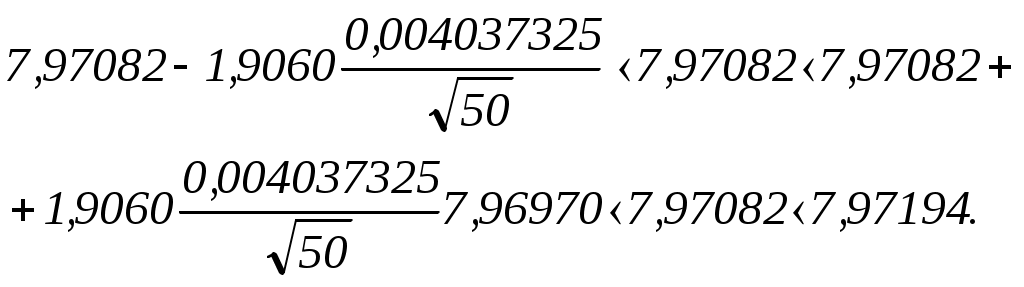

;



8. Построим гистограмму и полигон частот (допускается с помощью программы «Excel» рис. 14, 15).

Рис. 14.	Рис. 15

9. Нанести на гистограмму и полигон частот данные (истинное значение физической величины, действительное значение физической величины, среднее арифметическое и границы доверительного интервала), затем сформулировать выводы. В пределах границ каждого интервала подсчитать количество измерений попадающих в каждый интервал и значения проставить на гистограмме и полигоне частот.

ЗАКЛЮЧЕНИЕ
Полученные в процессе выполнения расчетно-графических работ навыки и знания обработки данных измерений какой-либо величины позволяют студенту научиться анализировать производственный процесс и принимать правильные решения на последующие действия.
ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. 
   Брянский Л.Н., Дойников А.С. Краткий справочник метролога. – М.: Издательство стандартов. 1991.
   
2. 
   Кушнир Ф.В., Сазенко В.Г. Электрорадиоизмерение. Л. Энергия, 1975г.
   
3. 
   Тейлор Дж. Введение в теорию ошибок. – М.: Мир, 1985.
   
4. 
   Сквайре Дж. Практическая физика. – М.: Мир, 1971.
   
5. 
   Худсон Д. Статистика для физиков. – М.: Мир, 1970.
   
6. 
   Кунце Х.-И. Методы физических измерений. – М.: Мир, 1989.
   
7. 
   Тойберт П. Оценка точности результатов измерений. М.: Энергоатомиздат, 1988.
   
8. 
   Крылова Г.Д. Основы стандартизации, сертификации, метрологии. – М.: ЮНИТИ, 2001. – 711 с.
   
9. 
   Сертификация. А.Г. Сергеев и др. Учебное пособие. 1999 г.
   
10. 
    Метрология, стандартизация и сертификация. А.Г. Сергеев и др. Учебное пособие. 2002 г.
    
11. 
    Артемьев Б.Г., Голубев С.М. Справочное пособие для работников метрологических служб: в 2-х кн. – М.: Изд-во стандартов, 1990. – Кн. 1. – 582 с.
    
12. 
    Кузнецов В.А., Петров В.А. Закон распределения погрешностей измерений с учетом времени эксплуатации измерительных приборов // Измерительная техника. – 1992. - № 7.
    
13. 
    Кузнецов В.А., Ялунина Г.В. Основы метрологии. – М.: ИПК Изд-во стандартов, 1995. – 278 с.
    
14. 
    Маркин Н.С. Практикум по метрологии. – М.; Изд-во стандартов, 1994. – 188 с.
    
15. 
    Савчук В.П. Обработка результатов измерений. Физическая лаборатория. Ч1: Учеб. пособ. для студентов вузов. – Одесса: ОНПУ, 2002.