КП 2013. Методические указания по выполнению курсового проекта (работы) для студентов, обучающихся по направлению 160100 Авиа и ракетостроение

• Название: Методические указания по выполнению курсового проекта (работы) для студентов, обучающихся по направлению 160100 Авиа и ракетостроение
• Анкор: КП 2013.doc
• Дата: 17.02.2017
• Размер: 5.18 Mb.
• Имя файла: КП 2013.doc
• Тип: Методические указания; #2825
• страница: 4 из 12

2.2. Краткие сведения по геометрии прямозубых цилиндрических передач

Передачу движения с помощью зубьев принято называть зубчатым зацеплением.

Основным кинематическим условием, которому должны удовлетворять профили зубьев, является постоянство мгновенного передаточного отношения, т.е. зубья шестерни (меньшего из пары колес) и колеса передачи должны иметь сопряженные профили. К тому же, зубья колеса должны быть нарезаны так, что бы они могли входить в зацепление с колесами того же модуля, имеющими любое число зубьев. Это достигается нарезанием зубьев инструментами на основе исходного контура (см.рис.11.2).

Кроме этого, для обеспечения высокого КПД, прочности и долговечности колес профили должны обеспечивать:

• 
  малые скорости скольжения;
  
• 
  достаточные радиусы кривизны в точках контакта и допускать изготовление нарезание простым инструментом.
  

Этим условием наиболее полно удовлетворяет эвольвентное зацепление.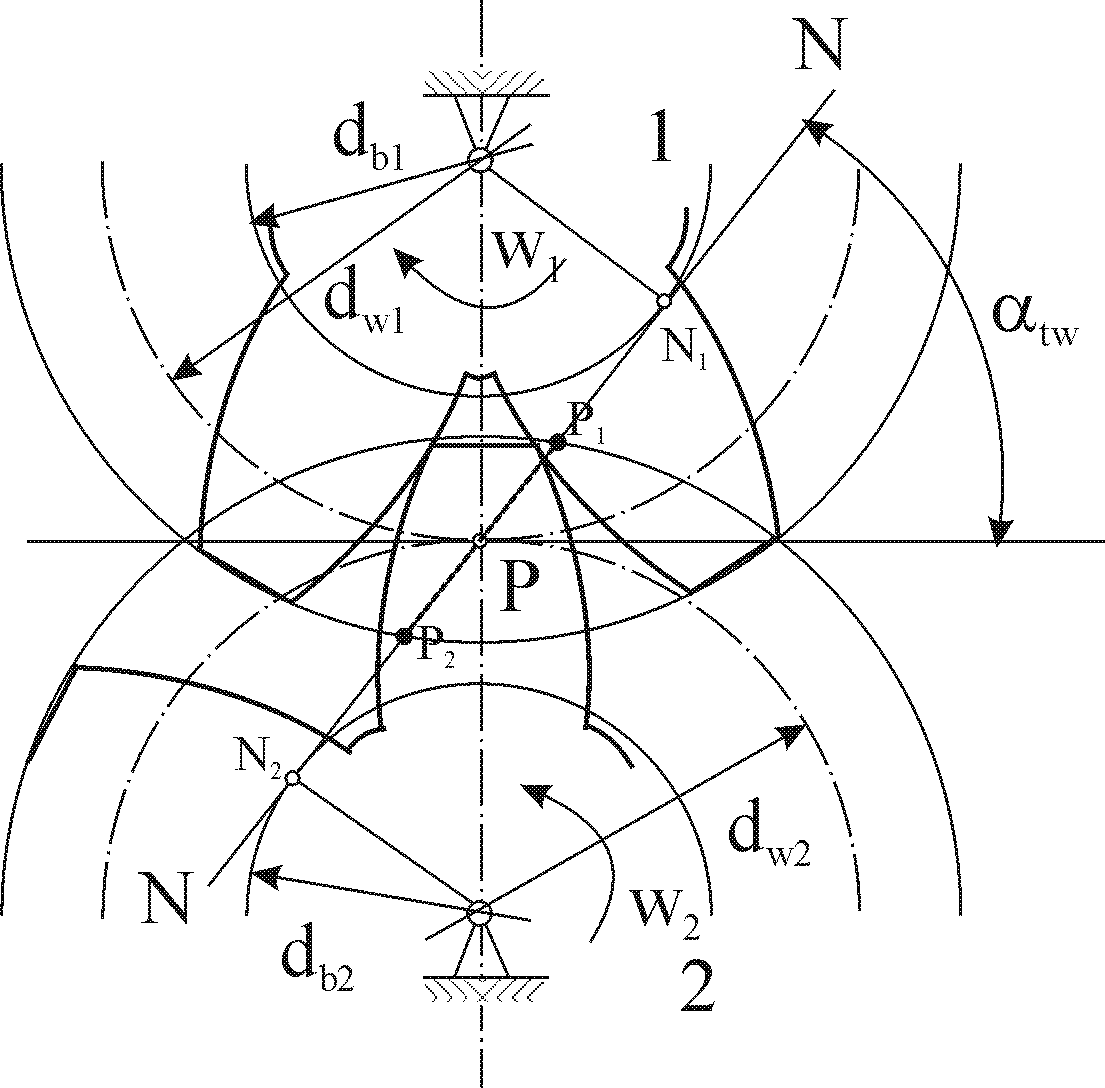



Рис 11.2. Образование эвольвентных профилей
Зацепление зубчатых колес эквивалентно качению без скольжения окружностей с диаметрами d_1 и d_2 (рис. 11.2), которые называются начальными окружностями. Если обкатывать прямую NN (рис. 11.2) по основным окружностям с диаметрами d_b1= d_1cos _t и d_b2= d_2cos _t (где _t – угол зацепления), то точки этой прямой опишут на каждом из колес эвольвенты. Поэтому нужное движение колес можно получить зацеплением зубьев, очерченных по эвольвенте. (При увеличении числа зубьев до  эвольвента превращается в прямую, а зубчатое колесо в рейку с трапециевидными зубьями.)

Одним из основных параметров зацепления является модуль (характеристика масштаба колеса):

m=Р/=d₁/z₁=d₂/z₂, (11.1)

где: Р – шаг зубьев, т.е. расстояние между одноименными профилями соседних зубьев рейки по делительной или другой параллельной ей прямой (делительная- это прямая, на которой теоретическая толщина зуба равна ширине впадин (рис.11.3);

d_1 и d_2 – диаметры делительных окружностей (начальных окружностей).

(Хотя различают окружной и делительный шаги, для прямозубых передач они равны).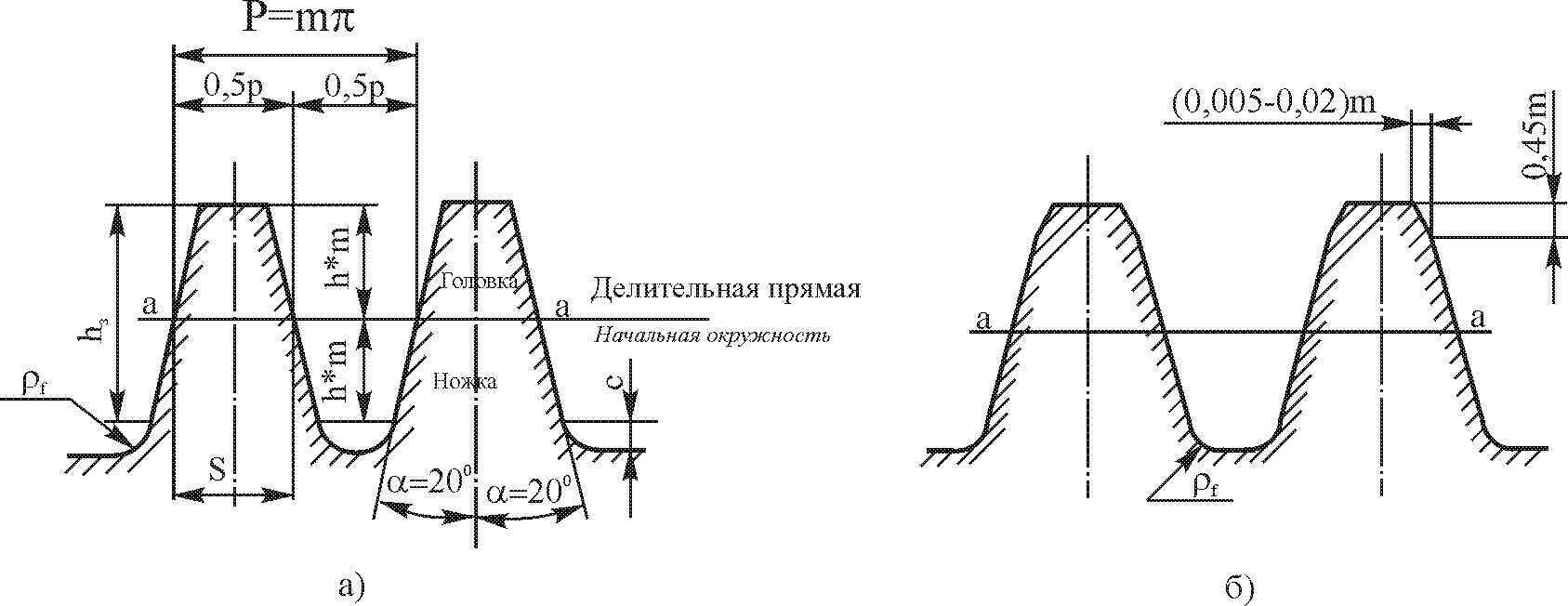


Рис. 11.3. Исходный контур
Модули стандартизованы в диапазоне 0.05...100 мм (ГОСТ 9563-80). Пример, 1; 1.25; 1.5; 2; 2.5; 3;4; 6;8.

Передаточное число – отношение числа зубьев колеса z₂ к числу зубьев шестерни z₁:

. (11.2)

Исходный контур для модулей больше 1 мм является прямобочным и имеет следующие параметры:

-профильный угол ;

-глубина захода h_з=2h_a*m (h_a =1 – коэффициент высоты головки зуба);

-толщина зуба по делительной прямой S=0.5P;

-радиальный зазор с=с^*m (с^*=1/4- радиального зазора);

-радиус закругления у корня зуба _I =0.384м.

Линия зацепления,т.е. геометрическое место точек контакта профилей зубьев при обкате, для колес с эвольвентным профилем зубьев является прямой. Точки Р₁ и Р₂ прямой NN (11.2.) – начало входа и выхода зубьев из зацепления, это точки пересечения окружностей по вершинам зубьев и линией зацепления. Линия зацепления нормальна к профилю зуба когда их точка пересечения проходит через полюс.

Перпендикуляры О₁N₁ и О₂N₂ из центров колес на линию зацепления дают радиусы d_b1 и d_b2 их основных окружностей.

Диаметры основных окружностей– диаметры окружностей, разверткой которых являются эвольвенты (профили) зубьев (d_b1; d_b2).

Межосевое расстояние передачи можно выразить и через диаметры основных и начальных окружностей:

; (11.3)

Полное зацепление – точка касания начальных окружностей.

Делительный диаметр d_=zm, где шаг зубьев=шагу на рейке;

Диаметр вершин зубьев d_a= (z+2)m

Диаметр впадины d_f= (z-2,5)m

Межосевое расстояние a_w=0.5(z₁+z₂)m

Толщина зуба S=0,5P=1,57m

Высота зуба h=2,25m

Окружной делительный шаг P_t=d_/z=m
Передаточные числа u обычно ограничивают габаритами передач. Для тихоходных и промежуточных передач u 5,6...6,3, для быстроходных передач u 6,3...8. Номинальные передаточные числа стандартизируют (1; 1,23; 1,5; 2; 2,5...).

Минимальное число зубьев шестерен обычно ограничивается условием неподрезания зубьев у основания. При нарезании зубьев без смещения можно изготовить колесо лишь с z_min17.

Ширину зубчатых колес выбирают в соответствии с установленными эмпирическими соотношениями _a=b/a_ для улучшенных сталей 0,315...0,4, для закаленных сталей 0,25...0,315. Стандартные значения _а: 0,1; 0,125; 0,16; 0,2; 0,315; 0,4.

Прямозубые колеса применяют при невысоких и средних окружных скоростях (6-20м/c), в планетарных передачах, при большой твердости зубьев.

Косозубые колеса применяют для ответственных передач при средних и высоких скоростях (10…30м/c). Угол наклона косозубых колес выбирают по условию, при котором осевой коэффициент перекрытия _=(btg)/P_n>1.1 (рис. 11.4).

где: P_n – нормальный шаг, кратчайшее расстояние по делительному цилиндру, (p_n= p_tcos). Обычно =8...22^o.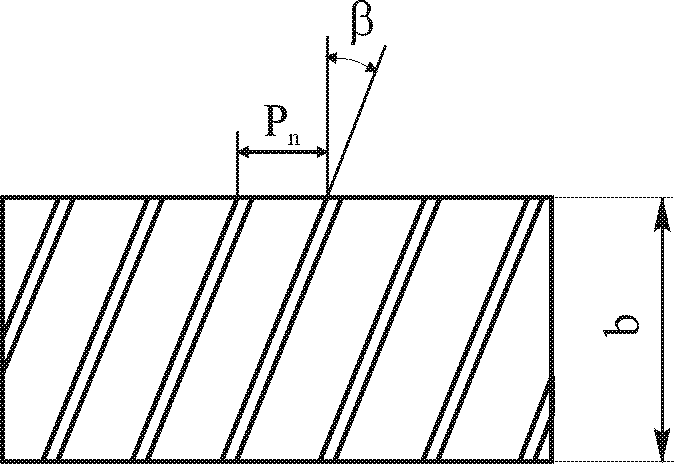

Рис.11.4. Косозубое колесо
Межосевое расстояние a_w, угол зацепления _tw, передаточное отношение u, число зубьев z, передаваемый момент T – основные параметры зубчатых передач. Их реализуют, изготавливая зубчатые колеса в соответствующих условиях и размерах.