КП 2013. Методические указания по выполнению курсового проекта (работы) для студентов, обучающихся по направлению 160100 Авиа и ракетостроение
 Скачать 5.18 Mb. Скачать 5.18 Mb.
|
2.6. Расчет зубьев на контактную прочностьРасчет сводится к удовлетворению условия, чтобы контактные, напряжения в зубьях H были равны или меньше допускаемых [H]. Расчет ведут для зацепления в полюсе, так как выкрашивание начинается у полюсной линии (на ножке), причем полюсная линия прямозубых передачах находится в зоне однопарного зацепления. В расчете полагают, что контакт двух зубьев аналогичен контакту двух цилиндров с радиусами 1 и 2, равными радиусам кривизны эвольвент зубьев в точке контакта (см. рис. 11.7), т.е. используется задача Герца о контакте цилиндров. По формуле Герца наибольшие контактные напряжения H МПа, при сжатии цилиндров вдоль образующих: где в применении к расчету зубьев 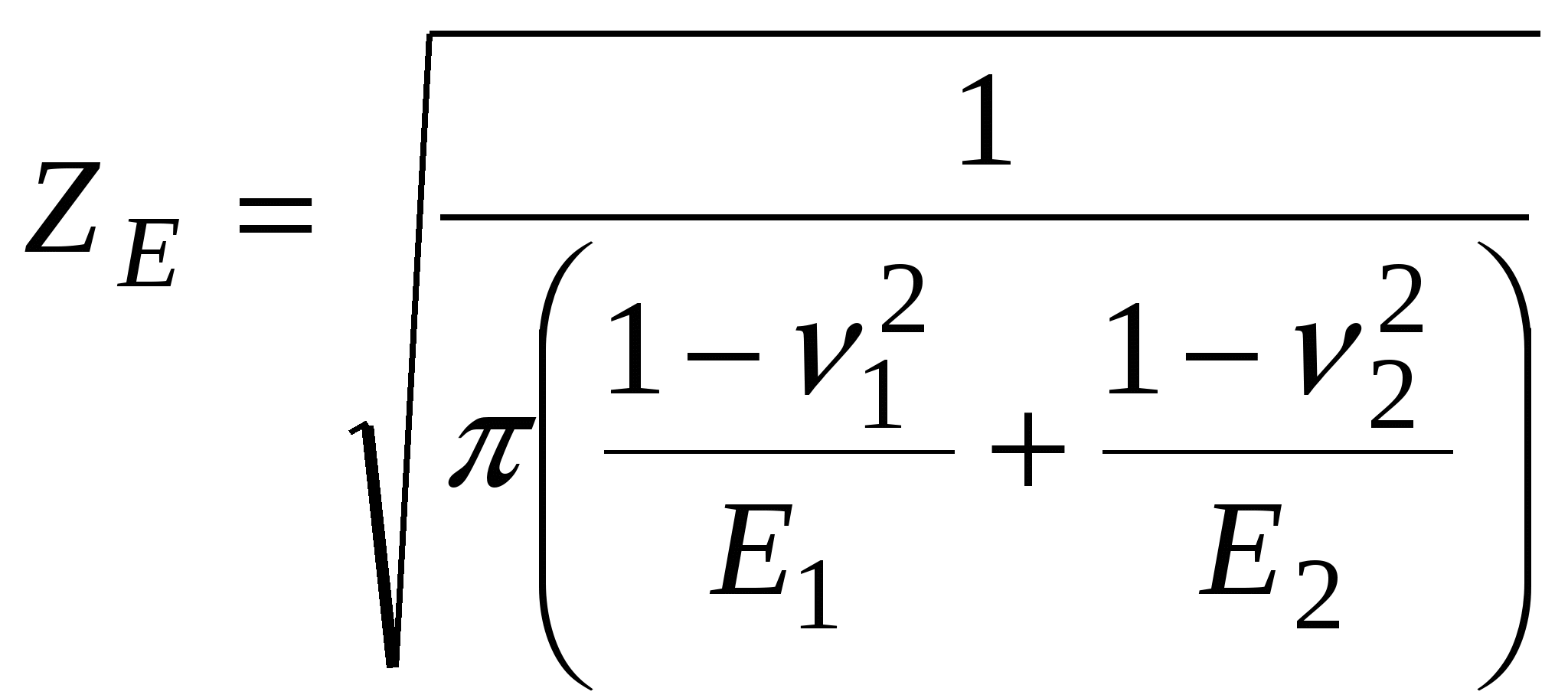 – коэффициент, учитывающий механические свойства материалов шестерни и колеса. – коэффициент, учитывающий механические свойства материалов шестерни и колеса.для стальных зубчатых колес коэффициент ZE = 190 МПа1/2; E1 и E2 – модули упругости материала шестерни и колеса (E1 = E2 = 2,1105 МПа); 1 и 2 – коэффициенты Пуассона (поперечного сжатия) материалов шестерни и колеса, равные для стали 0,3, а для чугуна 0,25;
Суммарную длину контактных линий можно найти по формуле: где: b – ширина колеса; n – число пар в зацеплении (в данном расчете n=1); – коэффициент перекрытия (=1,1); Прямозубые передачи. В прямозубых передачах длина контактных линий l меняется в процессе зацепления от рабочей ширины венца b, (в зоне однопарного зацепления) до 2b (в зоне двух парного зацепления). Для расчетов в соответствии с результатами экспериментов принимают 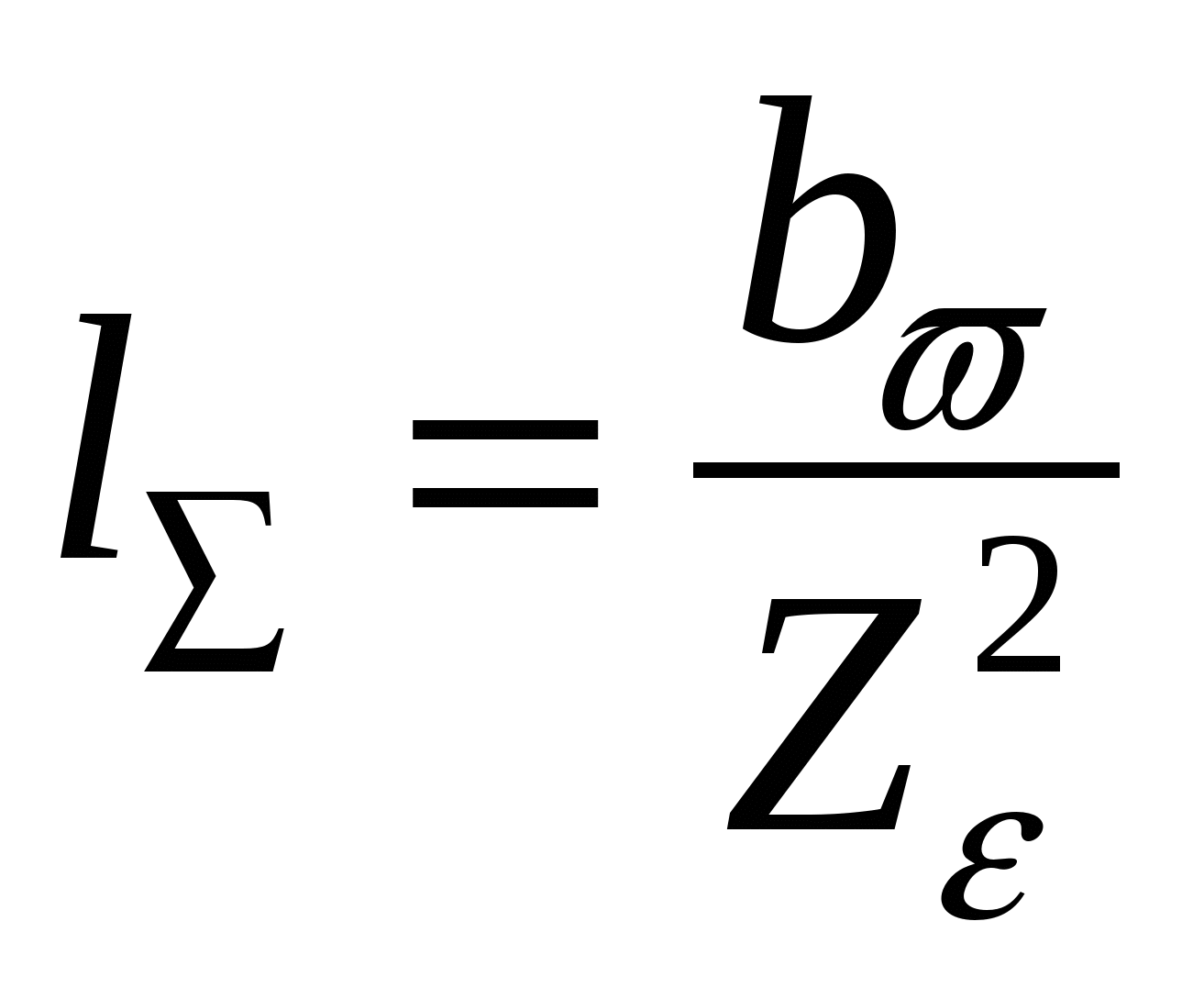 , где , где При изменение коэффициента перекрытия от 1,25 до 1,9 коэффициент Z меняется от 0.84 до 0.96. Для приближенных расчетов Z = 0,9, что соответствует = 1,6. Нормальная нагрузка на единицу длины контактных линий с учетом, что Fn = Ft/cost: 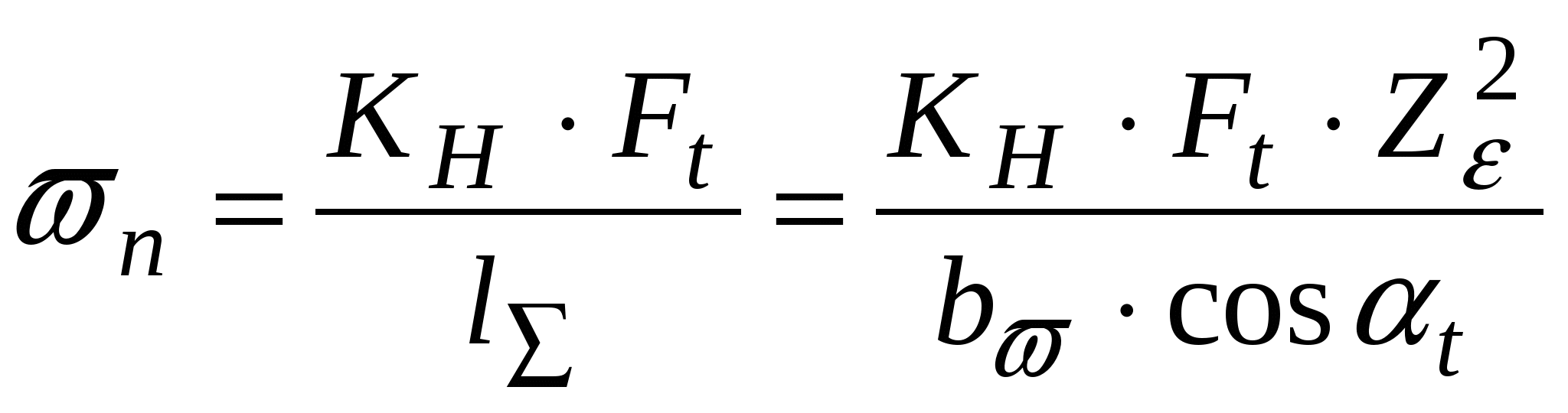 . . Радиусы кривизны профилей зубьев шестерни и колеса (рис.11.6.): 1=0,5d1sint; 2=0,5d2sint. Приведенный радиус кривизны: 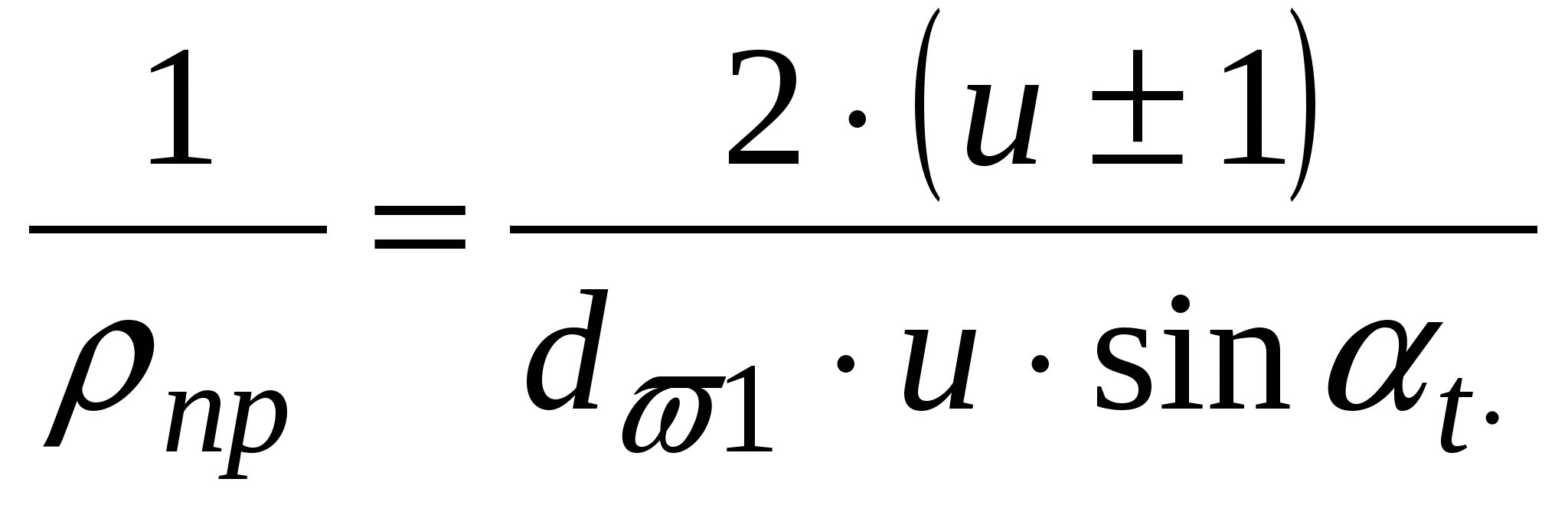 ; ; вспоминая, что u=d2/d1. Подставив в формулу Герца (11.12) выражения для n и 1/пр получаем основную формулу для расчета прямозубых передач на контактную прочность: где: Н0 – напряжение при номинальной нагрузке (Кн=1); При проектировании передач из расчета на контактную выносливость зубьев определяется минимально допустимая величина межосевого расстояния w. |

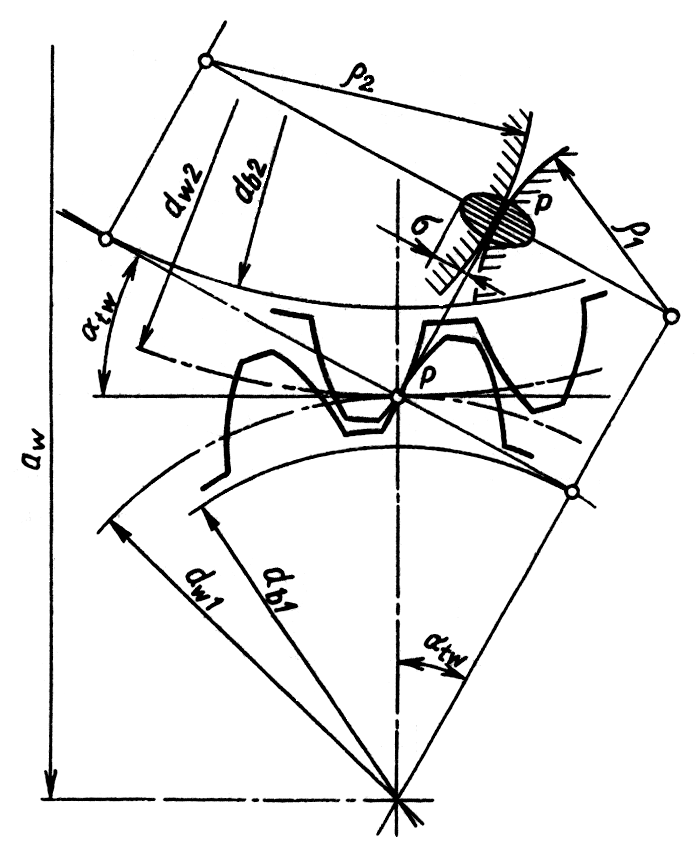
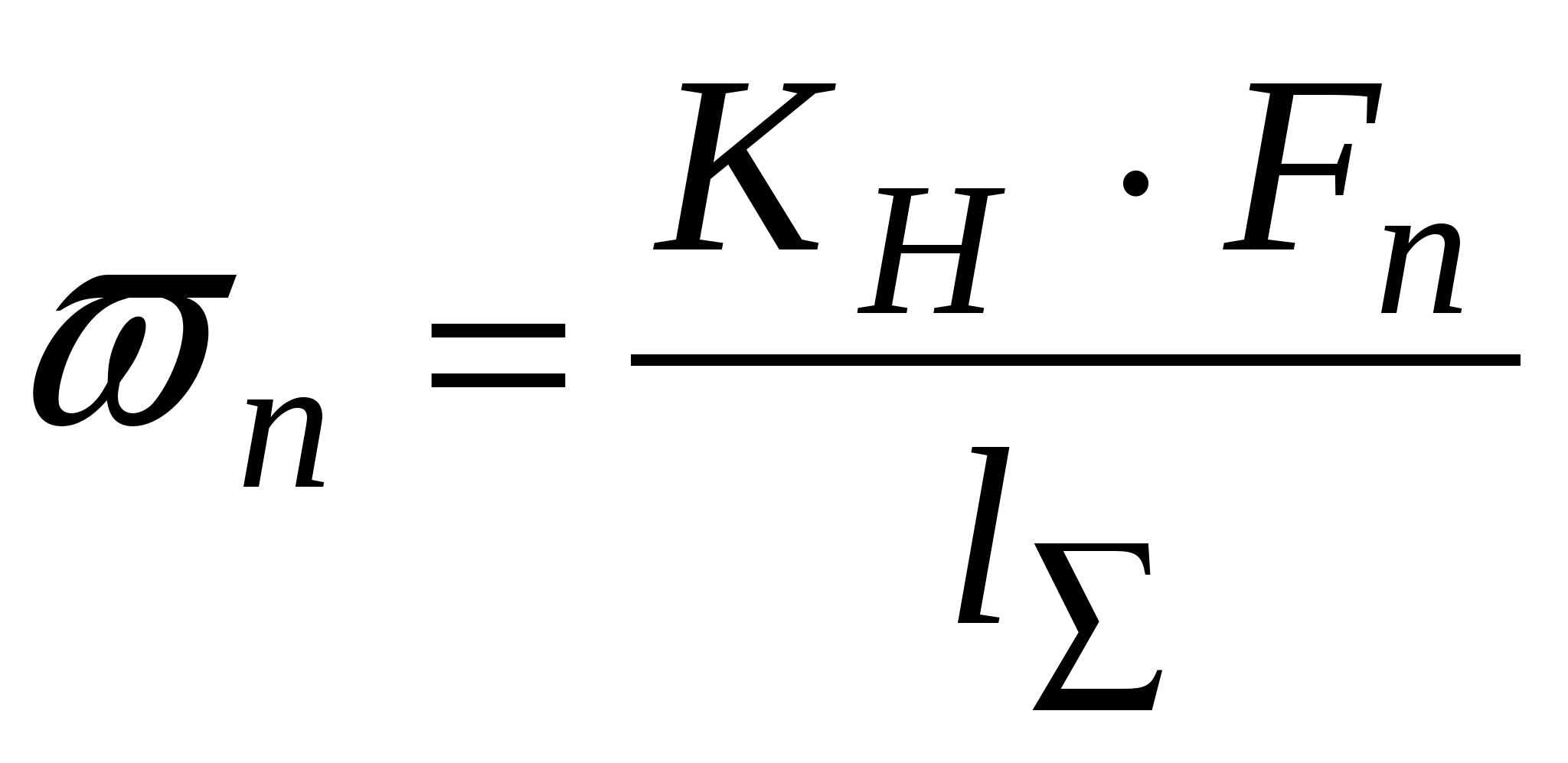 - нормальная нагрузка на единицу длины контактных линий;
- нормальная нагрузка на единицу длины контактных линий;